Einführung
Die gebräuchlichste elliptische Gleichung ist die Poisson-Gleichung.
Viele mathematisch-physikalische Probleme werden auf die Lösung dieser Gleichung reduziert, beispielsweise die Probleme der stationären Temperaturverteilung in einem Festkörper, Diffusionsprobleme, die Probleme der Verteilung des elektrostatischen Feldes in einem nichtleitenden Medium in Gegenwart elektrischer Ladungen und viele andere.
Um elliptische Gleichungen bei mehreren Messungen zu lösen, werden numerische Methoden verwendet, um Differentialgleichungen oder deren Systeme in algebraische Gleichungssysteme umzuwandeln. Die Genauigkeit der Lösung wird durch den Schritt des Koordinatengitters, die Anzahl der Iterationen und das Bitgitter des Computers bestimmt [1].
Der Zweck der Veröffentlichung ist es, eine Lösung der Poisson-Gleichung für die Dirichlet- und Neumann-Randbedingungen zu erhalten, um die Konvergenz der Relaxationsmethode der Lösung anhand von Beispielen zu untersuchen.
Die Poisson-Gleichung bezieht sich auf Gleichungen vom elliptischen Typ und hat im eindimensionalen Fall die Form [1]:
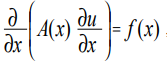
(1)
wobei x die Koordinate ist; u (x) ist die gewünschte Funktion; A (x), f (x) sind einige stetige Koordinatenfunktionen.
Wir lösen die eindimensionale Poisson-Gleichung für den Fall A = 1, die in diesem Fall die Form annimmt:
(2)
Im Intervall [xmin, xmax] definieren wir ein einheitliches Koordinatengitter mit einem Schritt Δ:
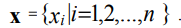
(3)
Die Randbedingungen der ersten Art (Dirichlet-Bedingungen) für das betrachtete Problem können wie folgt dargestellt werden:
(4)
wobei x1, xn die Koordinaten der Grenzpunkte der Region sind [xmin, xmax]; g1, g2 - einige
Konstanten.
Die Randbedingungen der zweiten Art (Neumann-Bedingungen) für das betrachtete Problem können wie folgt dargestellt werden:
(5)
Durch Diskretisierung der Dirichlet-Randbedingungen auf einem einheitlichen Koordinatengitter (3) unter Verwendung der Finite-Differenzen-Methode erhalten wir:
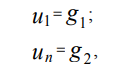
(6)
wobei u1, un die Werte der Funktion u (x) an den Punkten x1 bzw. xn sind.
Durch Diskretisierung der Neumann-Randbedingungen auf dem Gitter (3) erhalten wir:
(7)
Durch Diskretisierung von Gleichung (2) für interne Gitterpunkte erhalten wir:
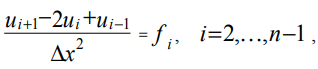
(8)
Dabei sind ui, fi die Werte der Funktionen u (x), f (x) am Gitterpunkt mit der Koordinate xi.
Als Ergebnis der Diskretisierung erhalten wir ein System linearer algebraischer Gleichungen der Dimension n, das n - 2 Gleichungen der Form (8) für interne Punkte der Region und die Gleichungen (6) und (7) für zwei Grenzpunkte enthält [1].
Das Folgende ist eine Python-Auflistung einer numerischen Lösung für Gleichung (2) mit den Randbedingungen (4) - (5) auf dem Gitter (3).
Listing Solutionfrom numpy import* from numpy.linalg import solve import matplotlib.pyplot as plt x0=0
Wir bekommen:
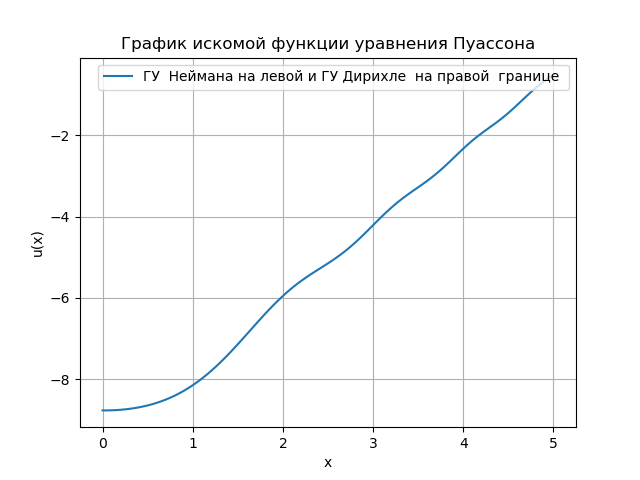
Das in Python entwickelte Programm eignet sich zur Analyse von Randbedingungen. Der obige Python-Lösungsalgorithmus verwendet die Numpy-Funktion - u = linalg.solve (a, bT) .T, um ein System algebraischer Gleichungen zu lösen, das die Geschwindigkeit mit der quadratischen Matrix {a} erhöht. Mit zunehmender Anzahl von Messungen ist es jedoch notwendig, auf die Verwendung von drei Diagonalmatrizen umzusteigen, deren Lösung selbst für eine sehr einfache Aufgabe kompliziert ist. Ich habe im Forum ein Beispiel gefunden:
Beispiel einer Lösung mit drei diagonalen Matrix from __future__ import print_function from __future__ import division import numpy as np import time ti = time.clock() m = 1000 A = np.zeros((m, m)) B = np.zeros((m, 1)) A[0, 0] = 1 A[0, 1] = 2 B[0, 0] = 1 for i in range(1, m-1): A[i, i-1] = 7 A[i, i] = 8 A[i, i+1] = 9 B[i, 0] = 2 A[m-1, m-2] = 3 A[m-1, m-1] = 4 B[m-1, 0] = 3 print('A \n', A) print('B \n', B) x = np.linalg.solve(A, B)
Das Programm der numerischen Lösung der Uniform in jeder Richtung des Gitter-Dirichlet-Problems für die Konvektions-Diffusions-Gleichung
[2]
(9)
Wir verwenden Näherungen durch zentrale Differenzen für den konvektiven Term und eine iterative Relaxationsmethode. Für die Abhängigkeit der Konvergenzrate vom Relaxationsparameter für die numerische Lösung des Problems mit f (x) = 1 und 6 (x) = 0,10. In der Rasteraufgabe:
(10)
Wir stellen die Matrix A als die Summe der diagonalen, unteren dreieckigen und oberen dreieckigen Matrizen dar:
(10)
Die Relaxationsmethode entspricht der Verwendung der iterativen Methode :
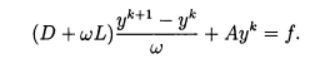
(11)
Bei
Ich spreche über obere Entspannung, wenn
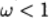
- über geringere Entspannung.
Programmliste from numpy import * """ - . .""" def relaxation(b, f, I1, I2, n1, n2, omega, tol = 1.e-8): h1 = I1 / n1 h2 = I2 / n2 d = 2. / h1**2 + 2. / h2**2 y = zeros([n1+1, n2+1]) ff = zeros([n1+1, n2+1]) bb = zeros([n1+1, n2+1]) for j in arange(1,n2,1): for i in arange(1,n1,1): ff [i,j] = f(i*h1, j*h2) bb[i,j] = b(i*h1, j*h2)
)
Wir bekommen:
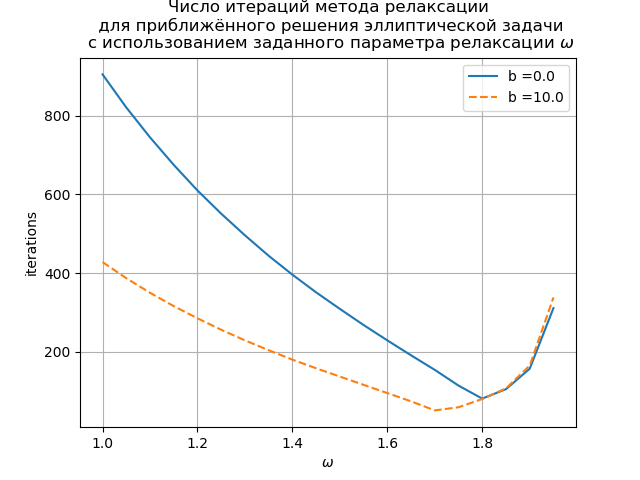
Die Grafik zeigt die Abhängigkeit der Anzahl der Iterationen vom Relaxationsparameter für die Poisson-Gleichung (b (x) = 0) und die Konvektions-Diffusions-Gleichung (b (x) = 10). Für die Poisson-Gittergleichung wird der optimale Wert des Relaxationsparameters analytisch ermittelt und die iterative Methode konvergiert bei
.
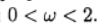
Schlussfolgerungen:
- Die Lösung des elliptischen Problems in Python mit einem flexiblen System zur Festlegung von Randbedingungen
- Es wird gezeigt, dass die Entspannungsmethode einen optimalen Bereich hat ( 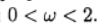) Entspannungsparameter.
Referenzen:
- Ryndin E.A. Methoden zur Lösung von Problemen der mathematischen Physik. - Taganrog:
Verlag der TRTU, 2003. - 120 p. - Vabishchevich P. N. Numerical Methods: Computational Workshop. - M.: Buchhaus
Librocom, 2010. - 320 S.