⏩ 🍾 🤾 Modellierung der Wasseroberfläche mit FFT und NeuroMatrix DSP-Prozessor 🚔 🏞️ 👩🏼‍🤝‍👨🏿

Die bekannte schnelle Fourier-Transformation wird seit langem nicht nur zur Lösung von Problemen der digitalen Signalverarbeitung, der Erkennung von Objekten im Bild, sondern auch in der Computergrafik verwendet. Jerry Tessendorf hat ein mathematisches Modell beschrieben , mit dem Sie Meereswellen synthetisieren und in Echtzeit animieren können. Dieses Modell basiert auf einer zweidimensionalen FFT.

Als ich mit der Entwicklung einer Anwendung für einen DSP-Prozessor beauftragt wurde, der den Betrieb einer FFT visualisiert, wurde mir klar, dass die Wellenmodellierung für diesen Zweck perfekt ist.

Mathematisches Modell der Welle

Die Grundidee eines mathematischen Modells einer Welle kann durch den Ausdruck beschrieben werden:

m a t h b f H

$\ mathbf H$ = FFT2D (

m a t h b f w i d e t i l d e H

$\ mathbf {\ widetilde H}$ ) Wird FFT2D als Operator einer zweidimensionalen FFT bezeichnet.

m a t h b f H

$\ mathbf H$ Ist das Höhenfeld der Wasseroberfläche (Matrixgröße

n_{1} x n_{2}

$n_1 x n_2$ wo

n_{1}

$n_1$ und

n_{2}

$n_2$ kann Werte von Zweierpotenzen annehmen). Elemente dieser Matrix sind Wellenhöhen.

m a t h b f w i d e t i l d e H

$\ mathbf {\ widetilde H}$ - Signal (Matrixgröße

n_{1} x n_{2}

$n_1 x n_2$ ), erzeugt nach einem bestimmten Gesetz und abhängig von der Zeit.

m a t h b f w i d e t i l d e H = m a t h b f w i d e t i l d e H_{0} . * m a t h b f A + o v e r l i n e m a t h b f w i d e t i l d e H_{0} . * o v e r l i n e m a t h b f A

$\ mathbf {\ widetilde H} = \ mathbf {\ widetilde H_0}. * \ mathbf A + \ overline {\ mathbf {\ widetilde H_0}}. * \ overline {\ mathbf A}$ wo die Elemente der Matrix

m a t h b f A

$\ mathbf A$ Das

$ inline $ e ^ {iω_ {ij} t} = cos⁡ (ω_ {ij} t) + isin (ω_ {ij} t) $ inline $ und die Matrix

o v e r l i n e m a t h b f A

$\ overline {\ mathbf A}$ - komplexes Konjugat zu

m a t h b f A

$\ mathbf A$ Matrix

i = 0, 1, . . . n_{1}, j = 0, 1, . . . n_{2}

$i = 0,1, ... n_1, j = 0,1, ... n_2$

ω_{i j}

$ω_ {ij}$ Sind Matrixelemente

L a r g e m a t h b f ω

$\ Large {\ mathbf ω}$ .

. *

$. *$ - elementweise Matrixmultiplikation.

m a t h b f w i d e t i l d e H_{0}

$\ mathbf {\ widetilde H_0}$ - Höhenfeld zum Anfangszeitpunkt t = 0.

o v e r l i n e m a t h b f w i d e t i l d e H_{0}

$\ overline {\ mathbf {\ widetilde H_0}}$ - komplexes Konjugat zu

m a t h b f w i d e t i l d e H_{0}

$\ mathbf {\ widetilde H_0}$ Matrix (Größe

n_{1} x n_{2}

$n_1 x n_2$ )

Um eine Animation der Bewegung von Wellen in Echtzeit zu erstellen, muss die Matrix neu berechnet werden

m a t h b f w i d e t i l d e H

$\ mathbf {\ widetilde H}$ und

m a t h b f H

$\ mathbf H$ t ändern. Matrizen

m a t h b f w i d e t i l d e H_{0}

$\ mathbf {\ widetilde H_0}$ ,

o v e r l i n e m a t h b f w i d e t i l d e H_{0}

$\ overline {\ mathbf {\ widetilde H_0}}$ und

L a r g e m a t h b f ω

$\ Large {\ mathbf ω}$ werden einmal berechnet und wiederverwendet.

Kommen wir nun zur Beschreibung des DSP-Prozessors, der auf der Grundlage der obigen Formeln in der Lage sein muss:

FFT berechnen.
Multiplizieren Sie Matrizen Element für Element.
Fügen Sie Matrizen hinzu.
Berechnen Sie den Vektor von Sinus und Cosinus.

Als DSP-Prozessor wurde 1879VM6Ya basierend auf der NeuroMatrix-Architektur verwendet, die vom wissenschaftlichen und technischen Zentrum "Module" CJSC entwickelt wurde. Die Schaltung in Abbildung 1.

Der Prozessor enthält zwei parallel laufende Kerne NMPU0 und NMPU1 (die mit einer Frequenz von 500 MHz arbeiten), von denen jeder einen RISC-Prozessor und einen Vektorkoprozessor (NMCore-FPU für Gleitkomma und NMCore INT für Ganzzahlarithmetik) aufweist. Der NMPU0-Kern ist für die Gleitkomma-Datenverarbeitung vorgesehen, und NMPU1 ist für ganzzahlige Daten vorgesehen. NMPU0 verfügt über 8 interne SRAM-Bänke (jeweils 128 kB) und NMPU1 über 4 Bänke (128 kB) desselben Speichers. Auf 1879VM6Ya sind ein DMA-Controller und eine DDR2-Schnittstelle installiert.

Bild

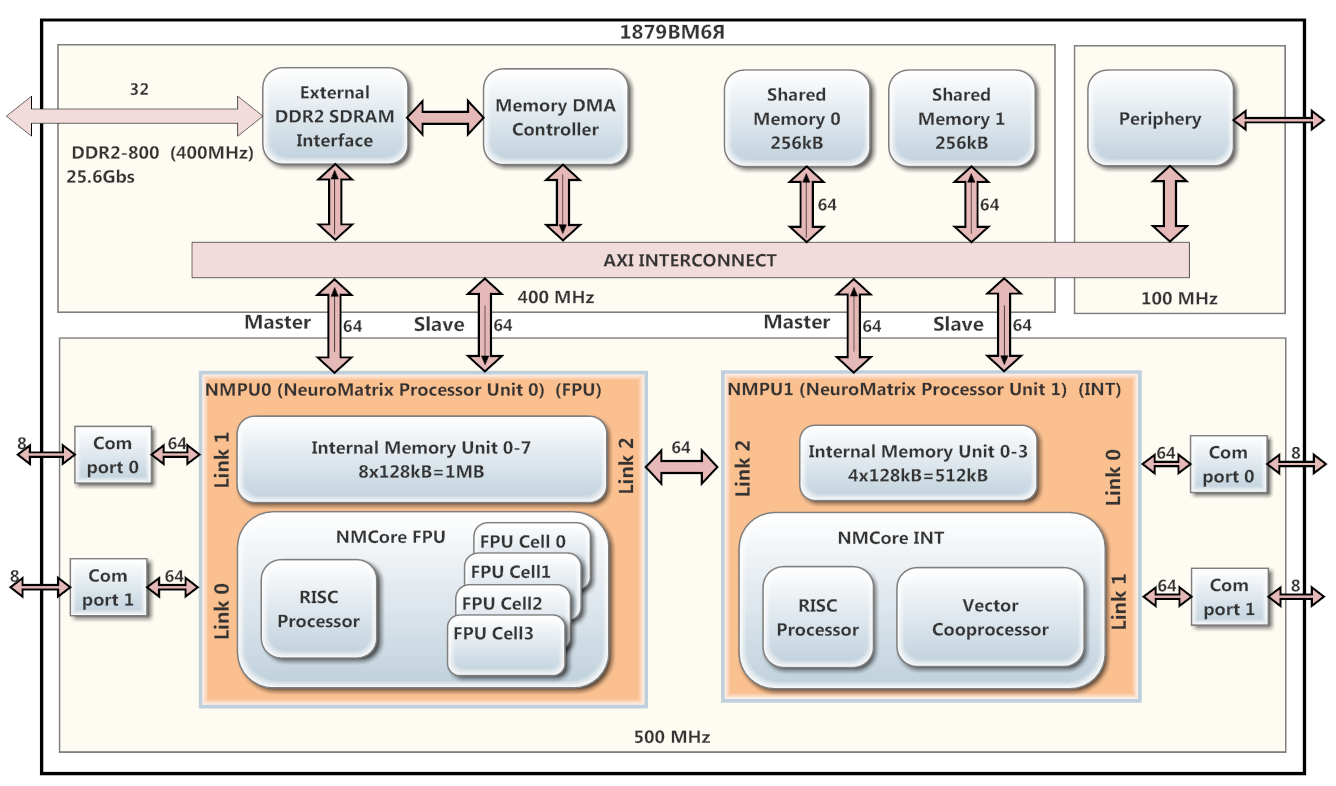Abb. 1. Prozessordiagramm 1879VM6YA

Der Prozessor befindet sich am Instrumentenmodul MC121.01 (siehe Abb. 2). Dieses Modul verfügt außerdem über 512 MB DDR2-Speicher.

Bild

Abb. 2. MS121.01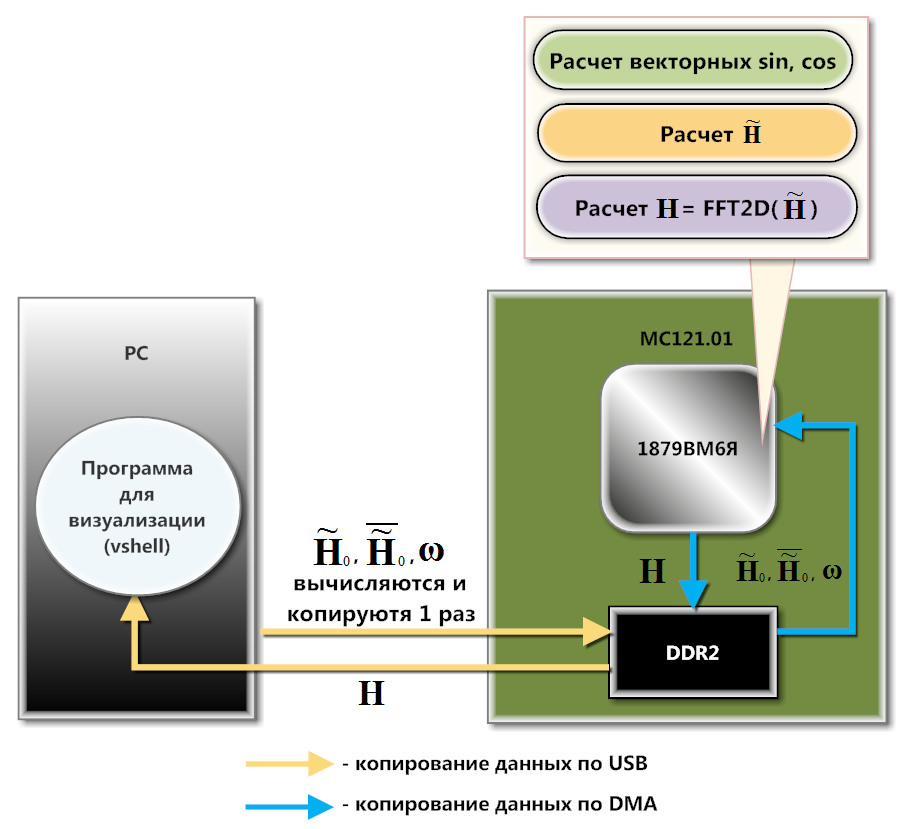

Abb. 3. Interaktionsschema von MC121.01 und PC

Der MC121.01 interagiert über USB mit dem PC (Abbildung 3). Auf Softwareebene wird diese Interaktion mithilfe der Download- und Datenaustauschbibliothek organisiert, die Teil des SDK dieser Karte ist. Vorberechnete Matrizen

m a t h b f w i d e t i l d e H_{0}

$\ mathbf {\ widetilde H_0}$ ,

o v e r l i n e m a t h b f w i d e t i l d e H_{0}

$\ overline {\ mathbf {\ widetilde H_0}}$ und

L a r g e m a t h b f ω

$\ Large {\ mathbf ω}$ werden über die Funktionen der Download- und Exchange-Bibliothek in den DDR2-Speicher geladen. DMA-Controller-Kopien

m a t h b f w i d e t i l d e H_{0}

$\ mathbf {\ widetilde H_0}$ ,

o v e r l i n e m a t h b f w i d e t i l d e H_{0}

$\ overline {\ mathbf {\ widetilde H_0}}$ und

L a r g e m a t h b f ω

$\ Large {\ mathbf ω}$ Zeile für Zeile in den internen Speicher (SRAM) des Prozessors. Das Herunterladen auf DDR2 beruht auf der Tatsache, dass keine dieser Matrizen vollständig in SRAM passt. Hier wird zeilenweise kopiert, da 1879BM6Ya aus dem SRAM schneller berechnet als aus dem DDR2. Darüber hinaus kann ein wesentlicher Teil der Berechnungen vor dem Hintergrund des DMA durchgeführt werden.

Unter Verwendung der Vektorfunktionen der NMPP-Bibliothek zur Berechnung von Sinus, Cosinus, Multiplikation und Addition von Vektoren berechnet der Prozessor die Matrixzeilen

m a t h b f w i d e t i l d e H

$\ mathbf {\ widetilde H}$ und nimmt ihnen die eindimensionale FFT ab. Das Ergebnis wird von DMA an DDR2 zurückgesendet. So wird in DDR2 eine Zwischenmatrix gebildet, aus deren Spalten der Prozessor die eindimensionale FFT berechnet (nach dem Laden der Spalten der Zwischenmatrix durch DMA in SRAM). Somit wird in DDR2 eine Matrix gebildet

m a t h b f H

$\ mathbf H$ . Diese Matrix wird auf den PC heruntergeladen, um ein einzelnes Bild mit dem Bild der Wellenoberfläche zu zeichnen. Um das Bild in Echtzeit zu animieren, müssen Sie die Matrix gemäß dem oben beschriebenen Algorithmus berechnen

m a t h b f H

$\ mathbf H$ durch Erhöhen des Parameters t .

In der Praxis stellt sich heraus, dass 1879–6 die Matrix berechnet

m a t h b f H

$\ mathbf H$ schneller als der PC es entleert. Aus diesem Grund ist der Prozessor möglicherweise inaktiv und wartet darauf, dass der PC den nächsten Datenstapel aufnimmt. Dieses Problem konnte mit einem Ringpuffer (der mehrere Matrizen enthielt) gelöst werden

m a t h b f H

$\ mathbf H$ ) in DDR2-Speicherkarte organisiert.

Auf Softwareebene wird mit dem DMA-Controller gearbeitet und der Ringpuffer wird mithilfe der HAL-Bibliotheksfunktionen (Hardware Abstraction Level) für NeuroMatrix-Prozessoren ausgeführt.

Wellenoberflächenvisualisierung

Wenn der DEM

m a t h b f H

$\ mathbf H$ In den PC-Speicher geladen, können Sie die Oberfläche visualisieren. Um es klarer darzustellen, müssen Sie x, y, z koordinieren und Punkte auf der Oberfläche beschreiben, multipliziert mit der Rotationsmatrix . Wir erhalten also die neuen Koordinaten der Oberfläche x ', y', z 'und drehen sie in einem bestimmten Winkel.

Durch Skalieren der neuen Koordinaten und Verbinden der Punkte entlang dieser mit geraden Linien können Sie die Animation der Meereswellen sehen (siehe Video unten). Zur Visualisierung der Oberfläche wird die Bibliothek verwendet, um das Bild auf dem vshell-Bildschirm anzuzeigen.

Fazit

Abschließend möchte ich sagen, dass die Berechnung und Übertragung über USB einer Matrix

m a t h b f H

$\ mathbf H$ Bei einer Größe von 256 x 256 Float-Zahlen werden ~ 4,7 Millionen Taktzyklen ausgegeben (72 Taktzyklen pro Float). Die Bildrate beträgt ~ 107. Wenn Sie die Zeit für die Datenübertragung über USB nicht berücksichtigen, kosten die Berechnungen ~ 2,5 Millionen Zyklen (38 Zyklen pro Float). Dies ist die Gesamtzeit, die der Prozessor 1879/6 für die elementweise Multiplikation und Addition von Matrizen, die Berechnung von FFT, Sinus, Cosinus und das Kopieren mit DMA benötigt. Diese Berechnungen werden vor dem Hintergrund der USB-Datenübertragung durchgeführt.

Die Differenz von 2,2 Millionen Taktzyklen (4,7 Millionen - 2,5 Millionen = 2,2 Millionen) zeigt an, dass USB im PC-MC121.01-System ein „Engpass“ ist und 1879VM6Ya ohne Empfang mit Berechnungen um 46% mehr geladen werden kann Drawdown FPS.

Ich möchte auch darauf hinweisen, dass vor dem Hintergrund der USB-Datenübertragung und der Berechnungen auf einem Coprozessor für einen Gleitkommawert ein Coprozessor für Ganzzahlarithmetik verwendet werden kann, der in dieser Aufgabe nicht verwendet wurde.

Die Tabelle zeigt die Leistung einiger Vektorfunktionen der nmpp-Bibliothek.

Funktion	Bars
Eindimensionale FFT, 256 Punkte	1770
Sinus, 256 Punkte	1400
Cosinus, 256 Punkte	1400

Referenzen:

NMPP - eine Bibliothek von Grundelementen für die NeuroMatrix-Architektur
HAL - Hardware-abhängige Abstraktionsbibliothek von NeuroMatrix
VSHELL - Bildverarbeitungs- und Anzeigebibliothek

Modellierung der Wasseroberfläche mit FFT und NeuroMatrix DSP-Prozessor

Mathematisches Modell der Welle

Wellenoberflächenvisualisierung

Fazit

Referenzen:

More articles: