Aufgaben aus dem Schulbuch I.

Teil I.
Teil II
Teil III

Betrachten Sie die algorithmische Lösung für Problem Nummer 38 aus dem Buch "Aufgaben für Kinder von 5 bis 15 Jahren".

Berechnen Sie den Betrag:

$$

$$\ frac {1} {1 \ cdot2} + \ frac {1} {2 \ cdot3} + \ frac {1} {3 \ cdot4} + ... + \ frac {1} {99 \ cdot100}$$

(mit einem Fehler von nicht mehr als 1% der Antwort)

Im Folgenden finden Sie einen Algorithmus zum Berechnen von Teilsummen dieser Reihe in Schema (Lisp) in drRacket (mit drRacket können Sie Berechnungen in gewöhnlichen Brüchen durchführen):

#lang racket (define series_sum ( lambda (n) (if (= n 0) 0 (+ (/ 1 (* n (+ n 1))) (series_sum(- n 1))) ) ) ) (series_sum 10) (series_sum 100) (series_sum 1000) (series_sum 10000) (series_sum 100000) (series_sum 1000000) (define series_sum_1 ( lambda (n) (if (= n 0) 0 (+ (/ 1.0 (* n (+ n 1.0))) (series_sum_1(- n 1.0))) ) ) ) (series_sum_1 10) (series_sum_1 100) (series_sum_1 1000) (series_sum_1 10000) (series_sum_1 100000) (series_sum_1 1000000) 

Die letzten beiden Beispiele drRacket wurden mit einem Fehler berechnet



Dieses Programm kann auf online ide ideone.com und codepad.org ausgeführt werden .



Wenn wir Teilsummen in gewöhnlichen Brüchen betrachten, können wir sehen, dass die Summe der Reihen ist

$$

$$\ frac {n} {n + 1}$$

Ich möchte Sie daran erinnern $$$\ lim \ frac {n} {n + 1} = \ frac {1} {1+ \ frac {1} {n}} = \ frac {1} {1} = 1$ bei $$$n \ to \ infty$

Der zweite Band des Kurses der Differential- und Integralrechnung 363 (4) befasst sich mit dem allgemeinen Fall

$$

$$\ sum \ frac {1} {(\ alpha + n) (\ alpha + n +1)} = \ frac {1} {\ alpha + 1}$$

Die Aufgabe aus dem Kurs "Mathematik für Entwickler":
Finden Sie die Anzahl der Mitglieder in einer Sequenz $$$\ frac {2n-1} {4n + 5}$ außerhalb des Intervalls liegen $$$(1- \ frac {1} {1000}; 1+ \ frac {1} {1000})$

Kommen wir zum Hauptthema des Artikels.

Betrachten wir noch ein Beispiel aus einem Problembuch.
43 . Die Anzahl der Kaninchen (Fibonacci) bildet eine Sequenz $$$(a_ {1} = 1), 1, 3, 5, 8, 13, 21, 34, ...,$ in dem $$$a_ {n + 2} = a_ {n + 1} + a_ {n}$ für alle $$$n = 1, 2, ...$ . Finden Sie den größten gemeinsamen Teiler von Zahlen $$$a_ {100}$ und $$$a_ {99}$ .

Antwort: Zwei benachbarte Fibonacci-Zahlen sind Koprime, d. H. $$$\ gcd (u_ {n + 1}, u_ {n}) = 1$
(gcd ist der größte gemeinsame Teiler, d. h. GCD).

“Beweis aus dem Buch“ Jenseits der Seiten eines Mathematiklehrbuchs ”[10-11]


In der nächsten Aufgabe müssen Sie den Goldenen Schnitt berechnen. $$$\ frac {\ sqrt {5} + 1} {2} \ ca. 1.618$ . [Dies ist das Seitenverhältnis einer Postkarte, das beim Schneiden eines Quadrats, dessen Seite die kleinere Seite der Postkarte ist, ähnlich bleibt.]

53 . Für eine Folge von Fibonacci-Zahlen $$$a_ {n}$ Aufgaben 43 finden die Grenze der Beziehung $$$\ frac {a_ {n + 1}} {a_ {n}}$ während des Strebens $$$n$ bis unendlich:

$$

$$\ frac {a_ {n + 1}} {a_ {n}} = 2, \ frac {3} {2}, \ frac {5} {3}, \ frac {8} {5}, \ frac { 13} {8}, \ frac {21} {13}, \ frac {34} {21}.$$

Betrachten Sie die Segmente, die die Unterschiede zweier benachbarter Mitglieder der Serie darstellen $$$\ frac {a_ {n + 1}} {a_ {n}}$ .

Sogar Mitglieder der Serie $$$\ frac {a_ {n + 1}} {a_ {n}}$ eine wachsende Sequenz darstellen $$$x_ {n}$

$$

$$\ frac {3} {2}, \ frac {8} {5}, \ frac {21} {13}, ...,$$

Seltsame Zeilenmitglieder $$$\ frac {a_ {n + 1}} {a_ {n}}$ eine abnehmende Sequenz darstellen $$$y_ {n}$

$$

$$2, \ frac {5} {3}, \ frac {13} {8}, ...,$$

Durch das eingebettete Intervall-Lemma (Verlauf der Differential- und Integralrechnung, 38)

$$

$$c = \ lim x_ {n} = \ lim y_ {n}$$

Für unsere Reihe an einem Punkt $$$c$ faire Gleichheit $$$\ frac {a_ {n + 2}} {a_ {n + 1}} = \ frac {a_ {n + 1}} {a_ {n}}$

Teilen $$$a_ {n + 2} = a_ {n + 1} + a_ {n}$ auf $$$a_ {n + 1}$ Wir bekommen die Gleichung $$$\ frac {a_ {n + 2}} {a_ {n + 1}} = 1 + \ frac {a_ {n}} {a_ {n + 1}}$ .
Durch Ersetzen $$$\ frac {a_ {n + 2}} {a_ {n + 1}} = x, \ frac {a_ {n}} {a_ {n + 1}} = \ frac {1} {x}$ Wir erhalten die quadratische Gleichung $$$x = 1 + \ frac {1} {x}$ .

Wenn wir im Geogebra- Programm die Punkte 2 und 2 verbinden $$$\ frac {3} {2}$ , $$$\ frac {3} {2}$ und $$$\ frac {5} {3}$ , $$$\ frac {5} {3}$ und $$$\ frac {8} {5}$ usw. - eine selbstähnliche Figur bekommen




Im Allgemeinen gibt es in Python einen Standardalgorithmus zur Berechnung von Fibonacci-Zahlen.
Dieser Algorithmus ist auf Python.org verfügbar

 def fib(n): a, b = 0, 1 while a < n: print(a) a, b = b, a+b fib(100) 

Sie können den Link überprüfen
Ändern Sie diesen Algorithmus so, dass eine Annäherung an den Goldenen Schnitt ausgegeben wird. Für zwei benachbarte Zahlen a und b teilen wir die Summe a + b durch b

 def fib(n): a, b = 0.0 , 1.0 while a < n: print((a+b)/b) a, b = b, a+b fib(100) 

Sie können den Link überprüfen

Hier sind einige Aufgaben aus dem SICP- Tutorial zum Goldenen Schnitt .


Das folgende Beispiel aus dem Aufgabenbuch "Aufgaben für Kinder von 5 bis 15 Jahren"
54 . Berechnen Sie die unendliche fortgesetzte Fraktion

$$

$$1 + \ frac {1} {2 + \ frac {1} {1+ \ frac {1} {2+ \ frac {1} {1+ \ frac {1} {2 + ...}}}}$$

UPD Betrachten Sie die Gleichung

$$

$$\ alpha = 1+ \ frac {1} {2 + \ frac {1} {\ alpha}}$$

Nach den Sätzen 236 und 235 aus dem Buch „Zahlentheorie“:

$$

$$\ alpha = \ frac {P_ {1} \ alpha + P_ {0}} {Q_ {1} \ alpha + Q_ {0}}$$

Wir erstellen eine Wertetabelle $$$P_ {n}$ und $$$Q_ {n}$ bei $$$n = 0,1:$



so dass $$$\ alpha = \ frac {3 \ alpha + 1} {2 \ alpha + 1}, 2 \ alpha ^ {2} - 2 \ alpha -1 = 0$

und seitdem $$$\ alpha> 0,$ dann

$$

$$\ alpha = \ frac {1 + \ sqrt {3}} {2}$$

Betrachten Sie das Problem aus dem Buch „Hinter den Seiten eines Mathematiklehrbuchs“ [10-11].
4 . Zeigen Sie diese Nummer $$$\ sqrt {1+ \ sqrt {1 + \ sqrt {1 + ...}}}$ gleich der Zahl $$$\ varphi$ Definieren des Goldenen Schnitts.

Betrachten Sie die Option $$$x_ {n} = \ sqrt {c + \ sqrt {c + ... + \ sqrt {c}}}$
Verlauf der Differential- und Integralrechnung, 35 (2)

Auf diese Weise $$$x_ {n + 1}$ erhalten von $$$x_ {n}$ nach der Formel

$$

$$x_ {n + 1} = \ sqrt {c + x_ {n}}$$

... Nach dem Hauptsatz Optionen $$$x_ {n}$ hat eine endliche Grenze $$$a$ . Um dies festzustellen, gehen wir in der Gleichheit an die Grenze

$$

$$x_ {n + 1} ^ {2} = c + x_ {n};$$

Wir kommen so $$$a$ erfüllt die quadratische Gleichung

$$

$$a ^ {2} = c + a$$

Diese Gleichung hat die Wurzeln verschiedener Vorzeichen; aber die Grenze, die uns interessiert $$$a$ kann nicht negativ sein, daher ist es genau gleich der positiven Wurzel:

$$

$$a = \ frac {\ sqrt {4c + 1} + 1} {2}$$

Daraus können wir schließen, dass der "goldene Schnitt" eine Lösung für die Gleichung ist $$$a ^ {2} = c + a$
bei $$$c = 1$ .


Ferner wird im Verlauf der Differential- und Integralrechnung 35 (3) ein Algorithmus zur Berechnung der inversen Zahl verwendet

Lass $$$c$ Ist eine positive Zahl und setzen $$$x_ {n} = cy_ {n}$ . Die oben beschriebene Rekursionsrelation wird ersetzt durch:

$$

$$y_ {n + 1} = y_ {n} (2 - cy_ {n})$$

Den Anfangswert nehmen $$$y_ {0}$ unter der Bedingung: $$$0 <y_ {0} <\ frac {1} {c}$ wir verstehen das $$$y_ {n}$ monoton ansteigend, wird dazu neigen $$$\ frac {1} {c}$ . Nach diesem Schema wird bei Zählmaschinen die inverse Zahl berechnet $$$c$ .

Algorithmus zur Berechnung der inversen Zahl $$$c$ in Python:
( Ideone.com und codepad.org )

 def reciprocal(c,y0,n): arr=[] for i in range(n): arr.append(y0) y0=y0*(2-c*y0) return arr 

Die wechselseitige Funktion nimmt eine Zahl als Eingabe $$$c$ Anfangswert $$$y_ {0}$ Anzahl der Iterationen $$$n$ und gibt ein Array von "Annäherungen" an die Zahl zurück $$$\ frac {1} {c}$ .
$$$y_ {0} = 0,1$ bei $$$c <10$
$$$y_ {0} = 0,01$ bei $$$10 <c <100$
$$$y_ {0} = 0,001$ bei $$$100 <c <1000$
usw.
Beispiele, wie die reziproke Funktion mit verschiedenen funktioniert $$$c$

 >>> reciprocal(3,0.1,10) 

[0,1, 0,17, 0,2533, 0,31411733000000003, 0,3322255689810133, 0,3333296519077525,
0,3333333332926746, 0,333333333333333333, 0,333333333333333333, 0,3333333333333333]

 >>> reciprocal(8,0.1,10) 

[0,1, 0,12, 0,1248, 0,12499968, 0,1249999999991808, 0,125, 0,125, 0,125, 0,125, 0,125]

 >>> reciprocal(5,0.1,10) 

[0.1, 0.15000000000000002, 0.18750000000000003, 0.19921875000000003, 0.19999694824218753, 0.1999999999534339, 0.20000000000000004, 0.1999999999999999998,
0,19999999999999998, 0,19999999999999998]

Geometrische Interpretation

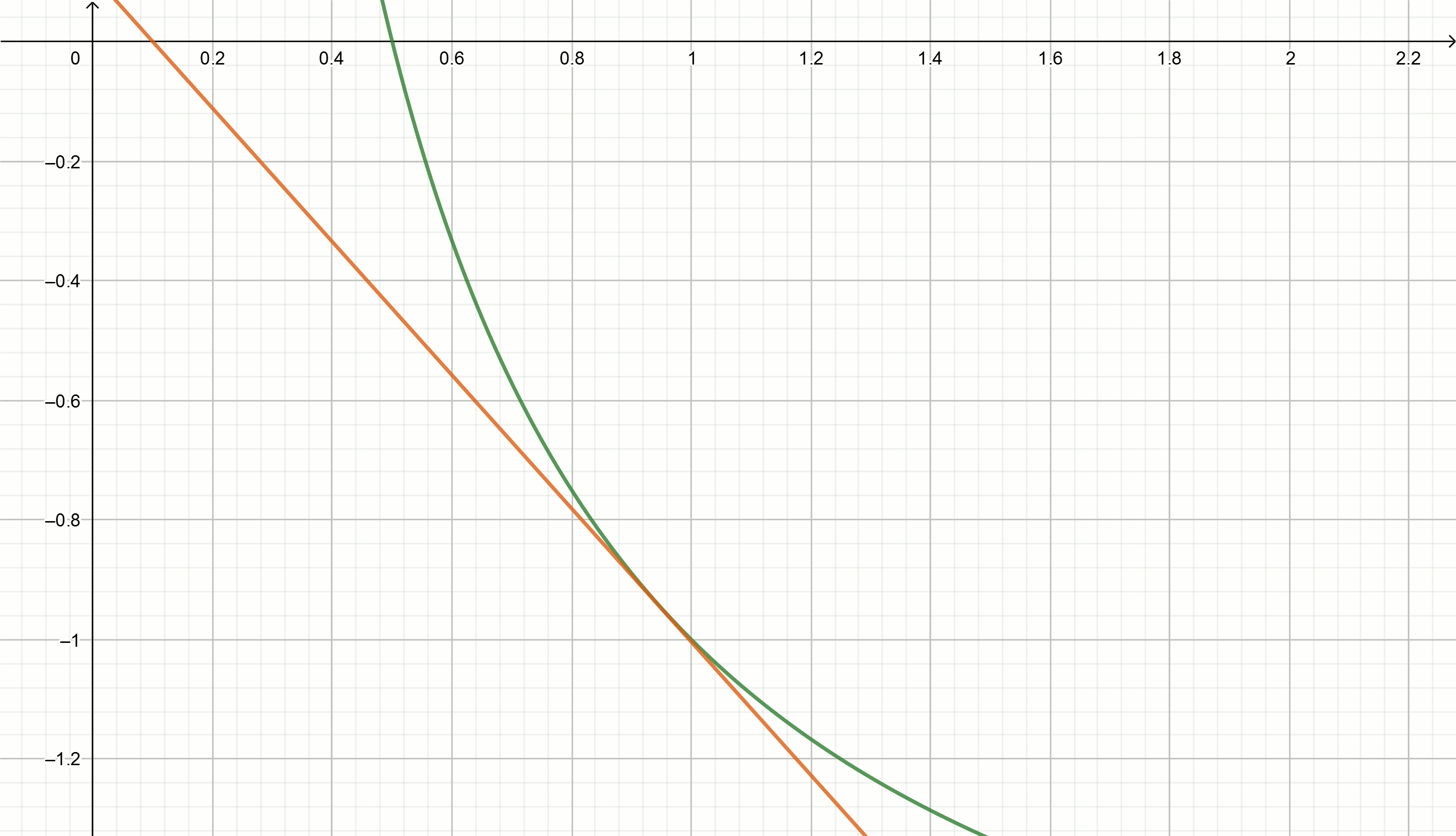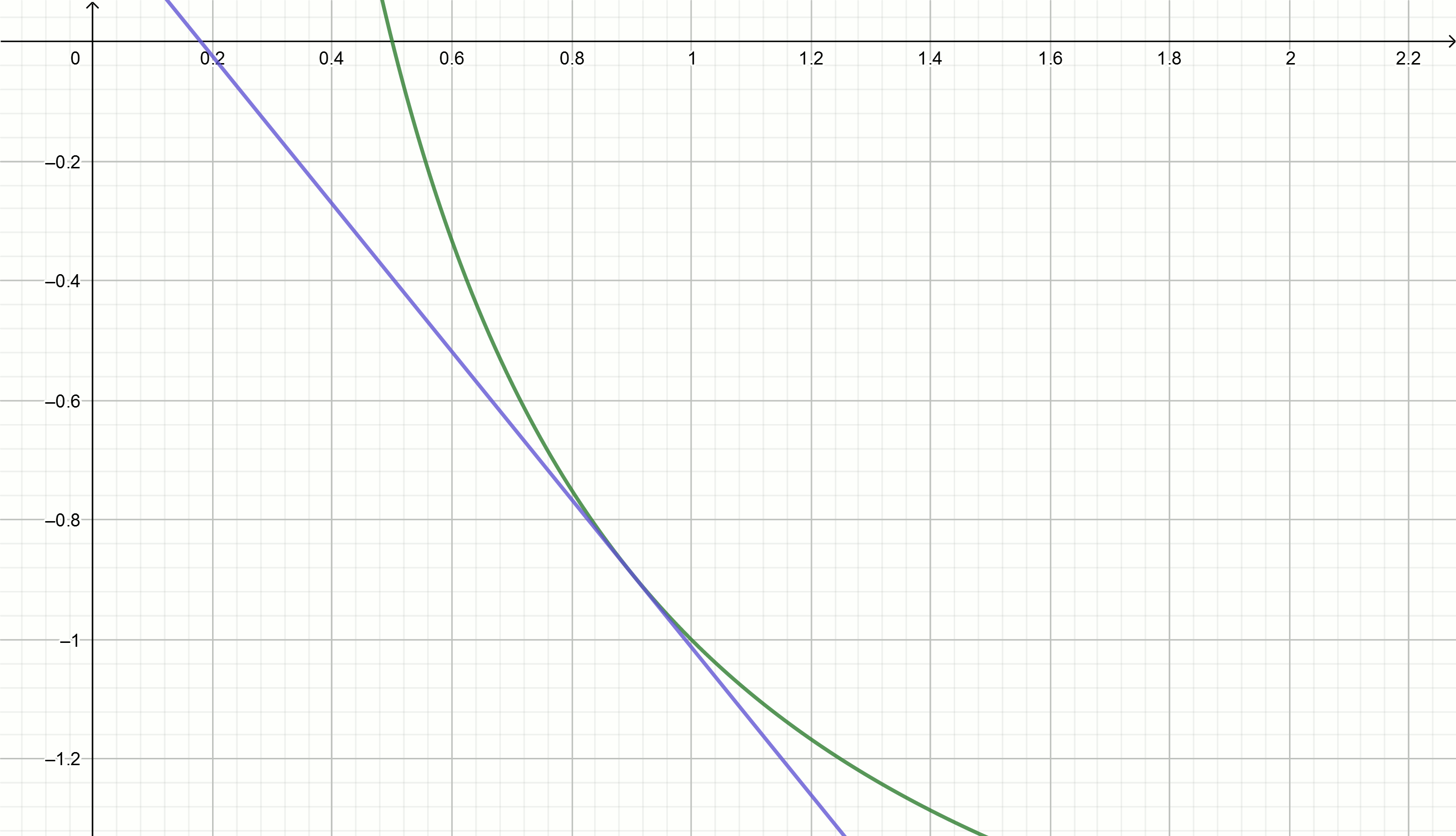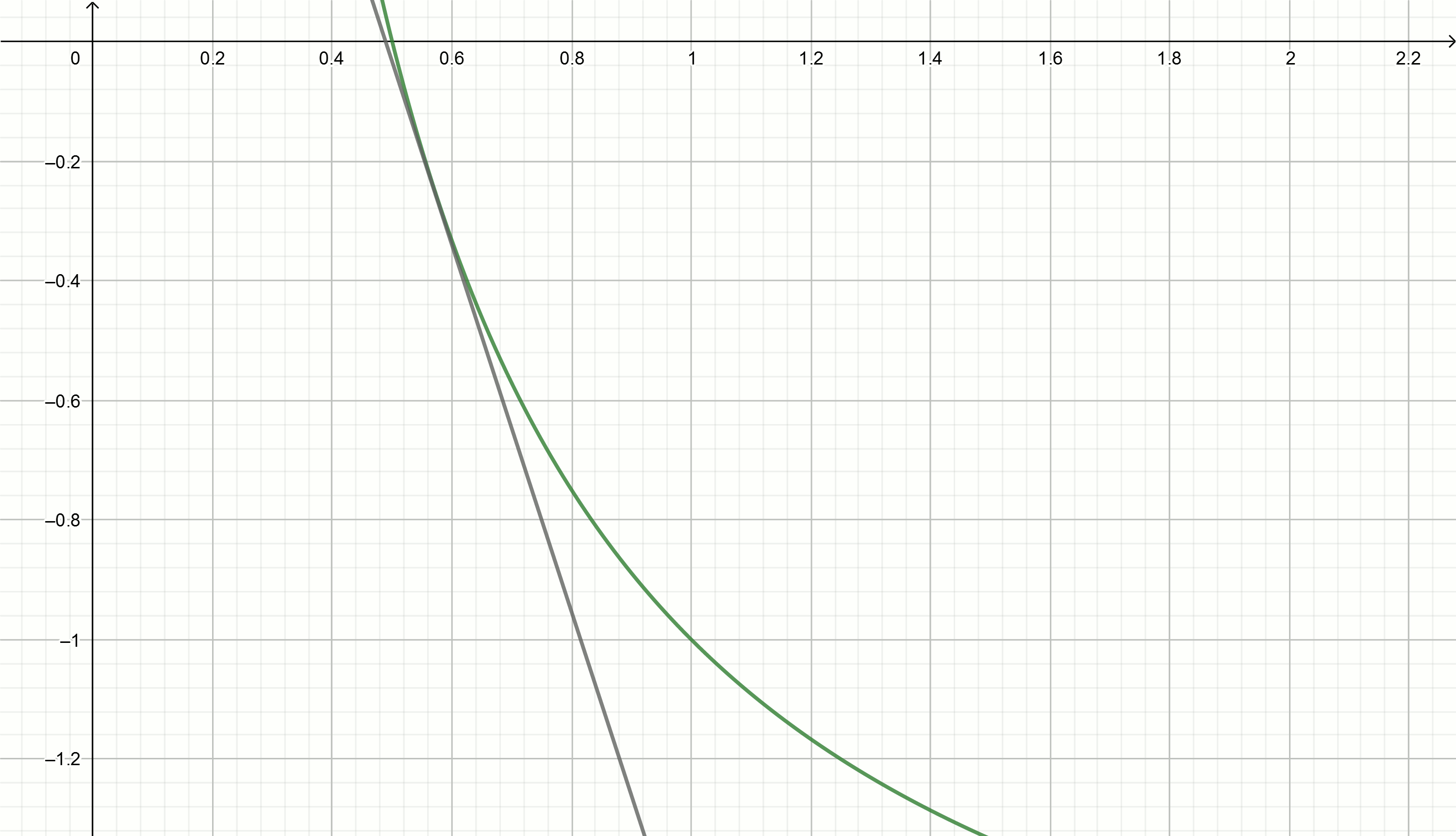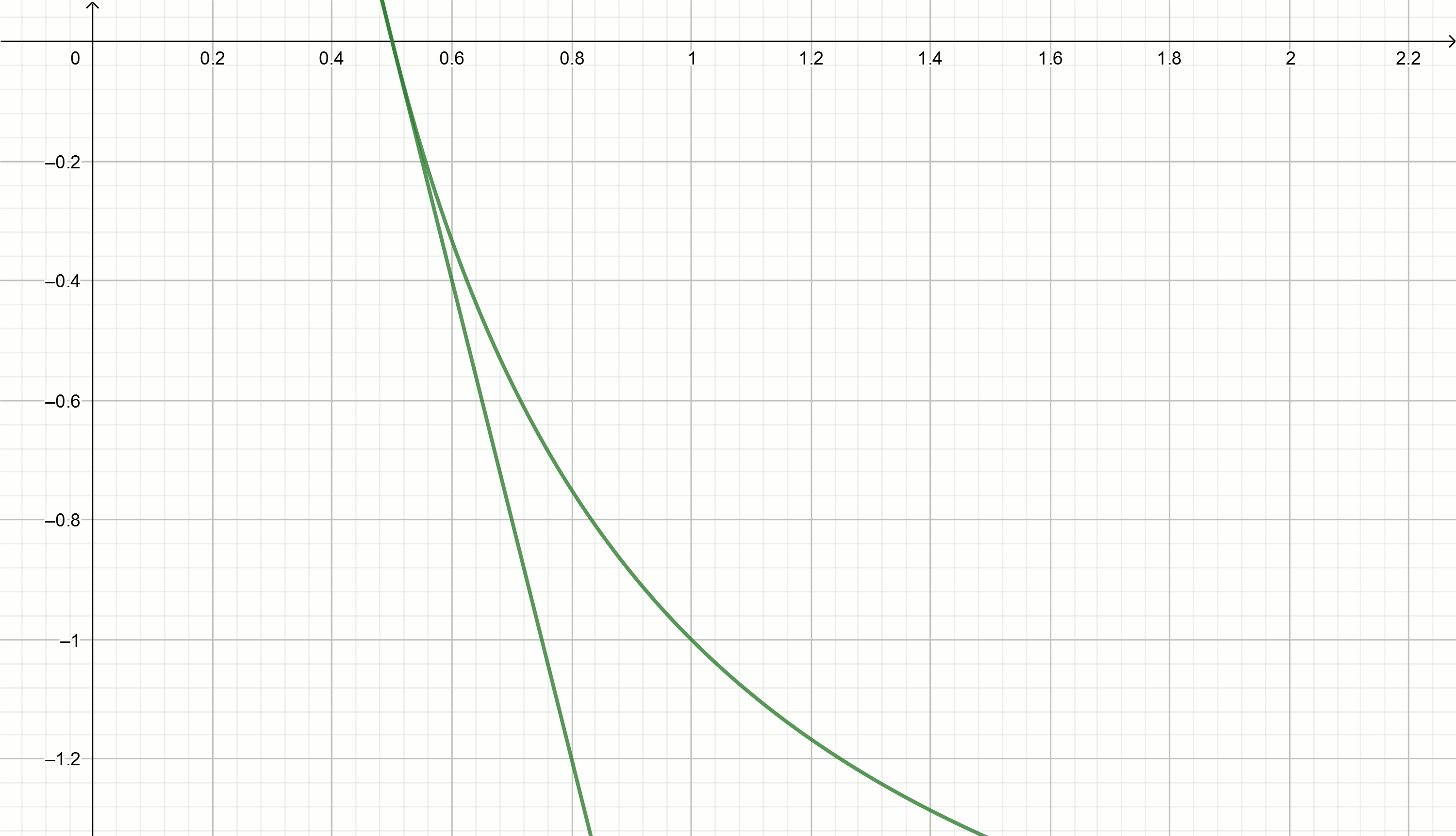
Versuchen wir, die Tangentenmethode zu verwenden, um die inverse Zahl zu approximieren.
Tangenten $$$y = f '(x_ {0}) (x-x_ {0}) + f (x_ {0})$ Graph zu funktionieren $$$y = \ frac {1} {x}$ werden durch die Formel ausgedrückt $$$y = \ frac {2} {x_ {0}} - \ frac {x} {x_ {0} ^ {2}}$

Zahlen ersetzen $$$1,2,3,4, ...$ statt $$$x_ {0}$ Wir erhalten die Gleichungen der Tangenten

$$

$$y = 2-x$$

$$

$$y = 1- \ frac {x} {4}$$

$$

$$y = \ frac {2} {3} - \ frac {x} {9}$$

$$

$$y = \ frac {1} {2} - \ frac {x} {16}$$

Erstellen Sie diese Diagramme


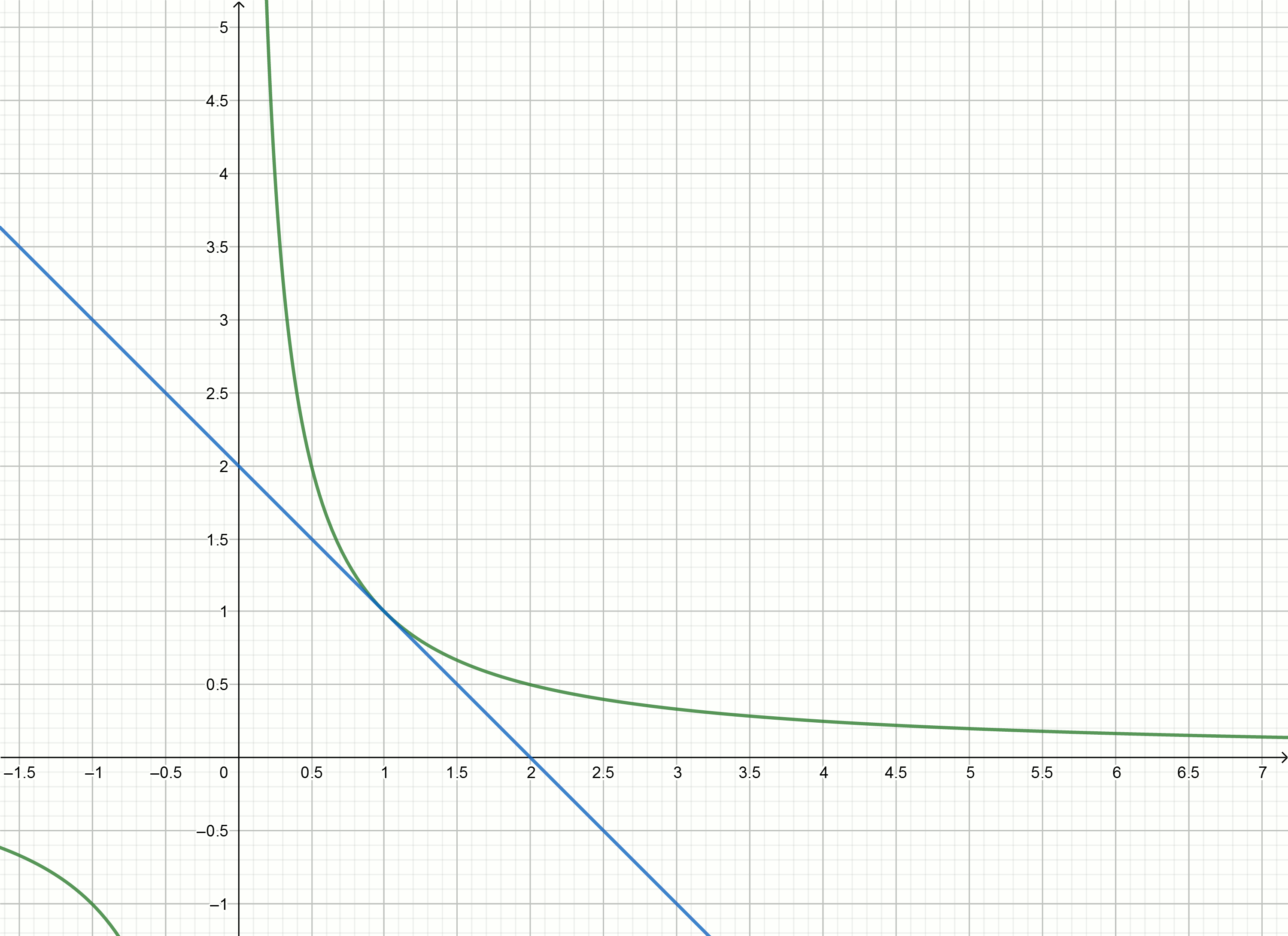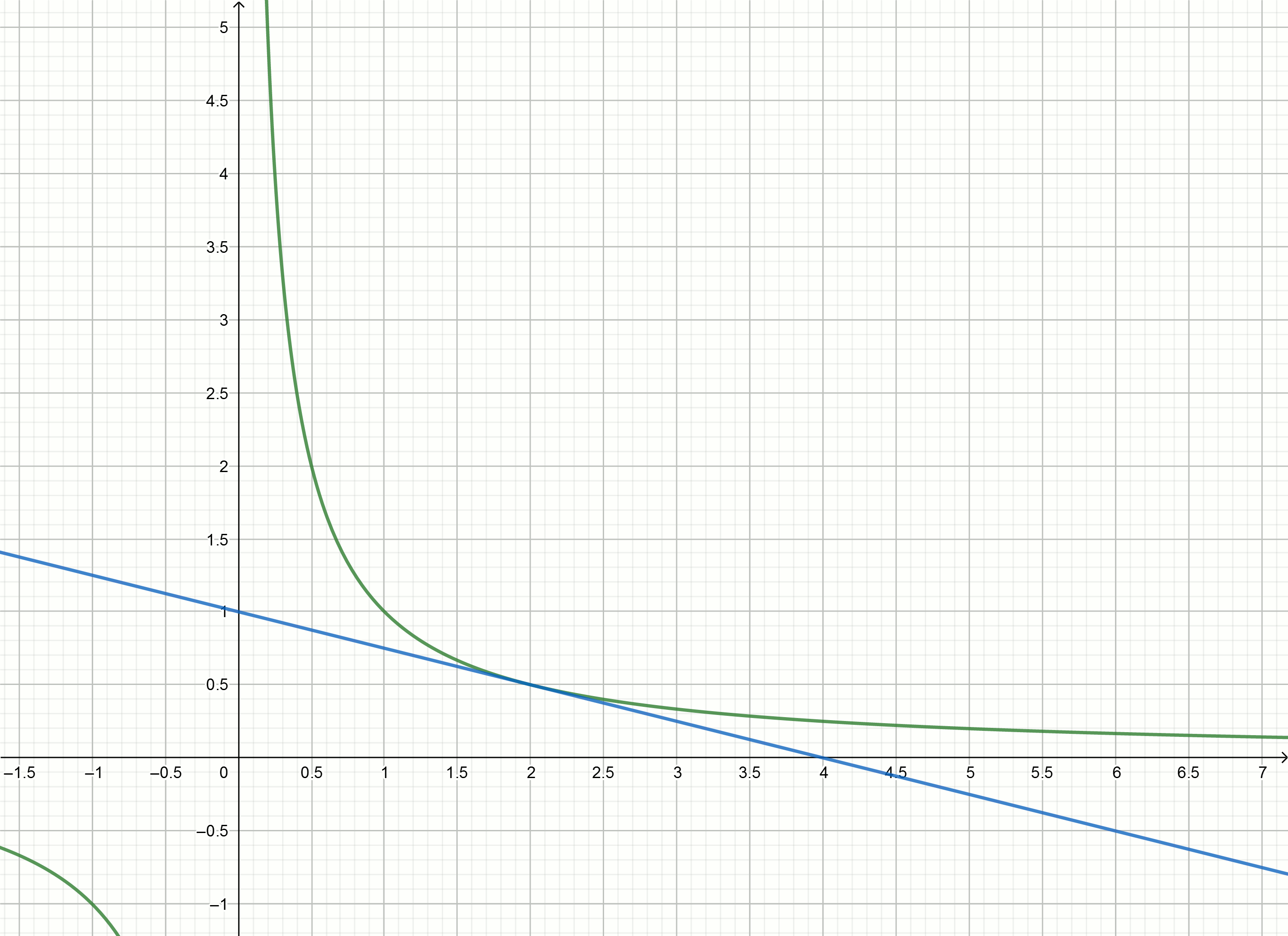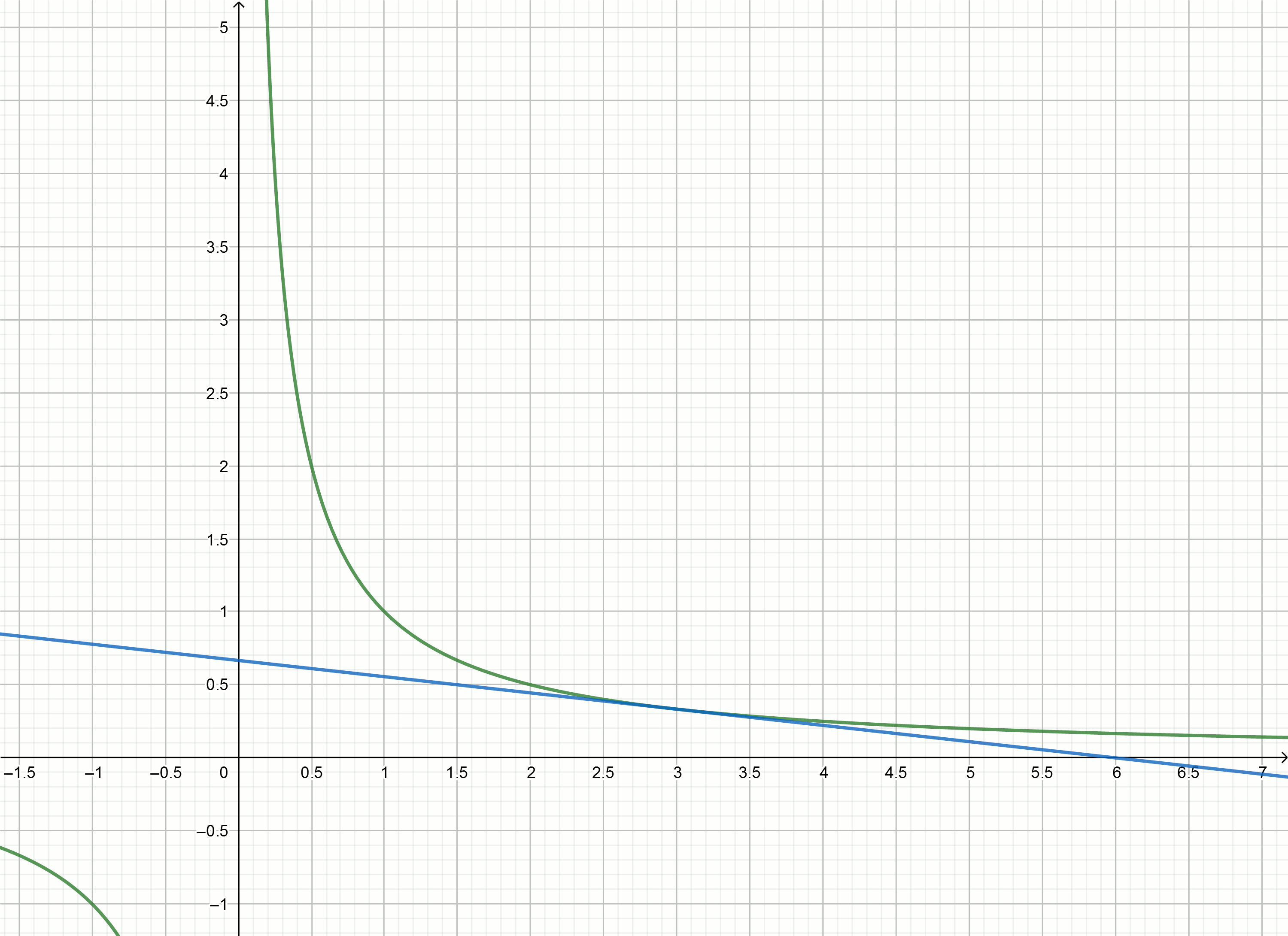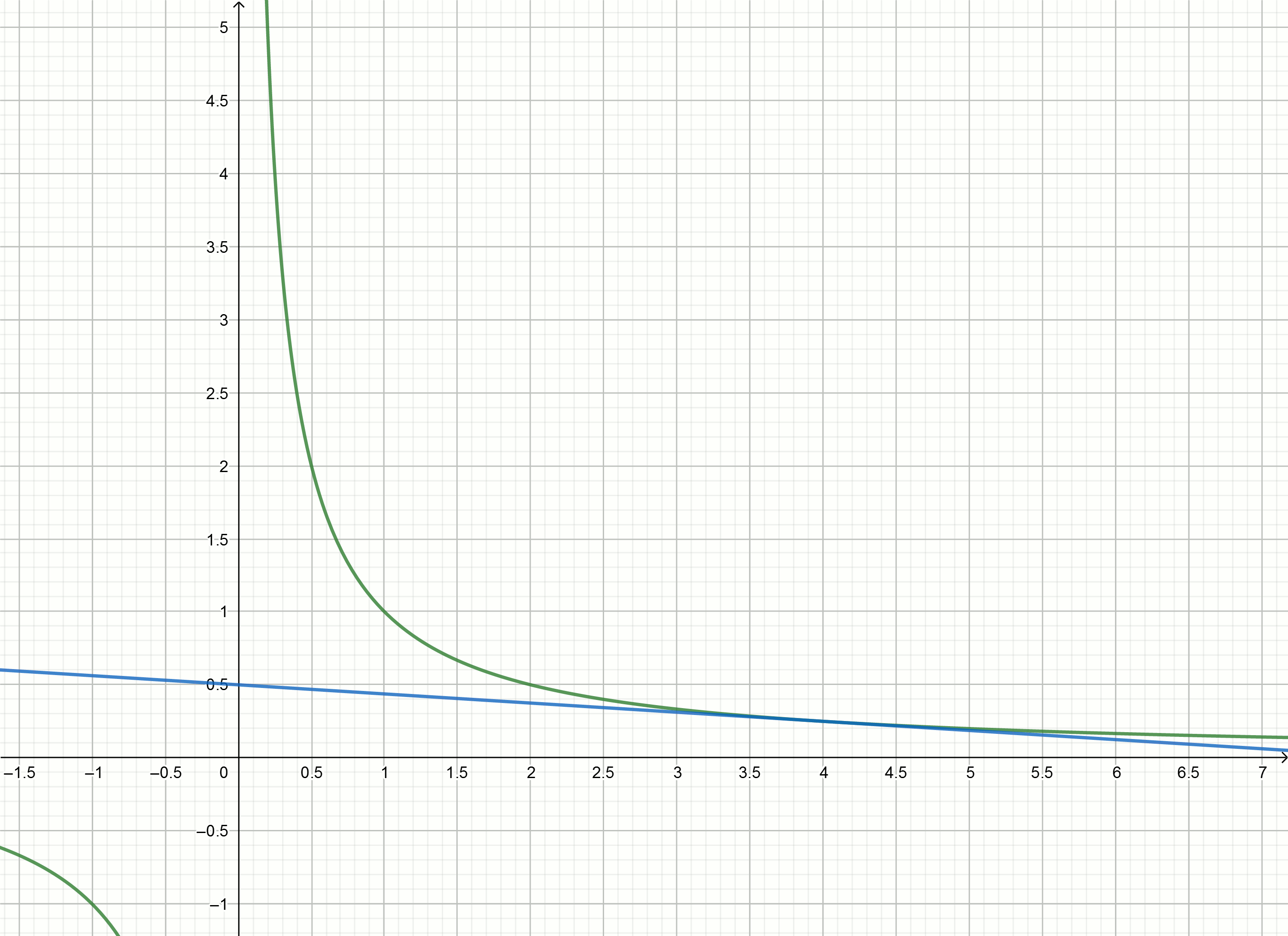
Wenn Sie die Hyperbel nach unten bewegen $$$\ alpha$ dann kreuzt es die Abszissenachse am Punkt $$$\ frac {1} {\ alpha}$ .
Die Tangentengleichung wird in konvertiert $$$y = \ frac {2} {x_ {0}} - \ frac {x} {x_ {0} ^ {2}} - \ alpha$
Ferner Gleichsetzen der Tangentengleichung mit Null und Ausdrücken $$$x$ Wir bekommen die Gleichung $$$x = x_ {0} - \ frac {f (x_ {0})} {f '(x_ {0})}$

Stattdessen $$$f (x_ {0})$ Ersatz $$$\ frac {1} {x_ {0}} - \ alpha$
Stattdessen $$$f '(x_ {0})$ Ersatz $$$- \ frac {1} {x_ {0} ^ {2}}$

Wir bekommen den Ausdruck $$$x = x_ {0} + (\ frac {1} {x_ {0}} - \ alpha) x_ {0} ^ {2}$
Wenn wir die Klammern erweitern, bekommen wir $$$x = x_ {0} + x_ {0} - \ alpha x_ {0} ^ {2}$

Ersatz $$$0.1$ in die Gleichung $$$x = x_ {0} (2- \ alpha x_ {0})$ und sehen, welche Werte "durchlaufen" werden $$$x$ bei $$$\ alpha = 2$ wir bekommen $$$0,1, 0,18, 0,29, 0,42, 0,49, 0,5$

Einsetzen dieser Werte in die Gleichung $$$y = \ frac {2} {x_ {0}} - \ frac {x} {x_ {0} ^ {2}} - 2$ wir werden direkt

$$

$$y = 0,111 - \ frac {x} {0,897}$$

$$

$$y = 0,222 - \ frac {x} {0,81}$$

$$

$$y = 0,816 - \ frac {x} {0,504}$$

$$

$$y = 0,857 - \ frac {x} {0,49}$$

$$

$$y = 1,5 - \ frac {x} {0,326}$$

$$

$$y = 2 - \ frac {x} {0,25}$$

Quadratwurzelextraktion

Zurück zu irrationalen Ausdrücken betrachten wir eine iterative Methode zum Extrahieren der Quadratwurzel.
Wir werden einen Algorithmus mit der iterativen Heron-Methode schreiben

$$

$$x_ {n + 1} = \ frac {1} {2} (x_ {n} + \ frac {a} {x_ {n}})$$

 def square_root(a,n): # a -  , n -   x0=1 #    1 arr=[] for i in range(n): arr.append(x0) #      x0=0.5*(x0+a/x0) #      return arr print square_root(2,10) 

codepad.org

Berechnung der Quadratwurzel unter Verwendung der von Rafael Bombelli verwendeten fortgesetzten Fraktionen

Um den Wert zu finden $$$\ sqrt {n}$ Zunächst definieren wir die gesamte Annäherung: $$$\ sqrt {n} = a \ pm r$ wo $$$0 <r <1$ . Dann $$$n = (a \ pm r) ^ {2} = a ^ {2} \ pm 2ar + r ^ {2}$ . Daraus lässt sich das leicht ableiten $$$r = {\ frac {| n-a ^ {2} |} {2a \ pm r}}$ . Ersetzen des resultierenden Ausdrucks in der Formel $$$\ sqrt {n} = a \ pm r$ erhalten wir eine fortgesetzte Fraktionserweiterung:

$$

$$a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac {| na ^ {2} |} {2a \ pm \ cdots}}}}}$$

Wir können also den Quadratwurzel-Extraktionsalgorithmus unter Verwendung der Zerlegung in einen fortgesetzten Bruch schreiben

 def square_root(n,a,n_count): # n- , a -    x0=a #    a arr=[] for i in range(n_count): #       a arr.append(x0-a) #  a x0=2*a+(na*a)/x0 return arr print square_root(2.0,1.0,10) 

codepad.org

Im Allgemeinen können reelle und komplexe Zahlen sowie Funktionen einer oder mehrerer Variablen private Zähler und Nenner sein.
Die Methode zum Extrahieren des ganzzahligen Teils ermöglicht es, eine irrationale Zahl in Form eines unendlichen fortgesetzten Bruchs mit Einheiten in den Zählern darzustellen (häufige Zähler gleich Eins).
Hier ist ein Beispiel für eine fortgesetzte fraktionierte Erweiterung einer Zahl $$$\ sqrt {5}$ aus dem Buch "Algebra"

$$

$$\ sqrt {5} -2 = \ frac {(\ sqrt {5} -2) (\ sqrt {5} +2)} {\ sqrt {5} +2} = \ frac {1} {\ sqrt { 5} +2}$$

Auf diese Weise, $$$\ sqrt {5} = 2+ \ frac {1} {\ sqrt {5} +2}$

Wählen Sie den ganzzahligen Teil der Zahl aus $$$\ sqrt {5} +2: E (\ sqrt {5} +2) = 4$ . Mittel $$$\ sqrt {5} +2$ kann dargestellt werden als $$$4 + \ alpha$ . Es ist klar, dass $$$\ alpha = \ sqrt {5} + 2-4 = \ sqrt {5} -2$ deshalb $$$\ sqrt {5} + 2 = 4 + \ sqrt {5} + 2$ . Wieder zerstören wir die Irrationalität im Zähler des zweiten Terms:

$$

$$\ sqrt {5} -2 = \ frac {1} {\ sqrt {5} +2}$$

Das Ergebnis ist:

$$

$$\ sqrt {5} = 2 + \ frac {1} {4+ \ frac {1} {\ sqrt {5} +2}}$$

Machen wir noch einen ähnlichen Schritt:

$$

$$\ sqrt {5} = 2 + \ frac {1} {4+ \ frac {1} {4+ \ frac {1} {\ sqrt {5} +2}}$$

Es ist leicht zu erkennen, dass der Prozess der Isolierung des gesamten Teils und der Bildung einer fortgesetzten Fraktion in diesem Beispiel kein Ende hat. In jedem neuen Nenner erscheint $$$4$ und Begriff $$$\ sqrt {5} -2$ . Daher ist es klar, dass $$$\ sqrt {5}$ wird als unendlicher fortgesetzter Bruch dargestellt:

$$

$$\ sqrt {5} = [2, 4, 4, 4, ...]$$

Hypothese

Wenn $$$d \ in \ mathbb {N}, \ sqrt {d} \ notin \ mathbb {N}$ dann der fortgesetzte Bruchteil der Zahl $$$\ sqrt {d} + [\ sqrt {d}]$ rein periodisch.
Evarist Galois hat diese Hypothese bewiesen.

Das heißt, wenn auf den nicht periodischen Teil der Fraktion $$$[1; 2,2,2, ...] = \ sqrt {2}$ füge den ganzen Teil hinzu $$$[\ sqrt {2}] = 1$ dann erhalten wir einen rein periodischen Bruchteil $$$[2,2,2, ...]$ .

$$$\ sqrt {3} = [1; 1,2, ...];$
$$$\ sqrt {3} +1 = [2,1, ...]$

$$$\ sqrt {5} = [2; 4,4,4, ...];$
$$$\ sqrt {5} +2 = [4,4,4, ...]$

$$$\ sqrt {6} = [2; 2,4, ...];$
$$$\ sqrt {6} +2 = [4,2, ...]$

$$$\ sqrt {13} = [3; 1,1,1,1,6, ...];$
$$$\ sqrt {13} +3 = [6,1,1,1,1,1, ...]$


Wenn in der Wurzel Zersetzung nach der Bombelli-Methode

$$

$$\ sqrt {n} = a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac {| na ^ { 2} |} {2a \ pm \ cdots}}}}}}$$

zum ersten Term hinzufügen $$$a$ erhalten wir einen rein periodischen Anteil

$$

$$\ sqrt {n} + a = 2a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac {| na ^ {2} |} {2a \ pm \ cdots}}}}}}$$

Es bleibt, den Bruch in eine bekanntere Form zu bringen (mit Einheiten im Zähler).
Teilen Sie den Zähler und den Nenner des Bruchs durch $$$| n-a ^ {2} |$ wir bekommen den Ausdruck

$$

$$\ sqrt {n} + a = 2 a \ pm {\ frac {1} {\ frac {2a} {| na ^ {2} |} \ pm {\ frac {1} {2a \ pm {\ frac { 1} {\ frac {2a} {| na ^ {2} |} \ pm \ cdots}}}}}}$$

Auf diese Weise

$$

$$\ sqrt {2} +1 = 2+ \ frac {1} {\ frac {2} {1} + \ frac {1} {2 + \ frac {1} {\ frac {2} {1} +. ..}}} = [2,2,2, ...]$$

$$

$$\ sqrt {3} +1 = 2+ \ frac {1} {\ frac {2} {2} + \ frac {1} {2 + \ frac {1} {\ frac {2} {2} +. ..}}} = [2,1, ...]$$

$$

$$\ sqrt {5} +2 = 4+ \ frac {1} {\ frac {4} {1} + \ frac {1} {4 + \ frac {1} {\ frac {4} {1} +. ..}}} = [4,4,4, ...]$$

$$

$$\ sqrt {6} +2 = 4+ \ frac {1} {\ frac {4} {2} + \ frac {1} {4 + \ frac {1} {\ frac {4} {2} +. ..}}} = [4,2, ...]$$

$$

$$\ sqrt {13} +3 = 6+ \ frac {1} {\ frac {6} {4} + \ frac {1} {6 + \ frac {1} {\ frac {6} {4} +. ..}}} = [6, \ frac {3} {2}, ...]$$

Wir werden ein Programm schreiben, das die fortgesetzte Bruchnäherung berechnet $$$[6, \ frac {3} {2}, ...]$

 #lang racket (define continued_fraction ( lambda (n) (if (= n 0) 1 (+ 6 (/ 1 (+ 3/2 (/ 1 (continued_fraction(- n 1)))))) ))) (continued_fraction 4) 

codepad.org
Im vierten Schritt bekommen wir $$$6 \ frac {3818} {6305}$ das ist gleich $$$6.60555114 ...$ , während $$$\ sqrt {13} +3 \ ca. 6.60555127$ .




PS Lösen Sie das Problem („Probleme für Kinder von 5 bis 15 Jahren“)
27 . Beweisen Sie, dass der Rest der Division einer Zahl $$$2 ^ {p-1}$ ungerade Primzahl
$$$p$ ist gleich $$$1$
(Beispiele: $$$2 ^ {2} = 3a + 1, 2 ^ {4} = 5b + 1, 2 ^ {6} = 7c + 1, 2 ^ {10} -1 = 1023 = 10 \ cdot 93)$ .
Dieses Problem wird in dem Artikel Amazing Adventures of Continued Fractions des Quantum-Magazins behandelt.

Bücher:
"Aufgaben für Kinder von 5 bis 15 Jahren" V. I. Arnold.
"Der Verlauf der Differential- und Integralrechnung" G. M. Fichtenholtz
"Zahlentheorie" A. A. Buchstab
"Hinter den Seiten eines Mathematiklehrbuchs" N. Ya. Vilenkin, L.P. Shibasov, Z.F. Shibasova
"Algebra" N. Ya. Vilenkin, R. S. Guter, S. I. Schwarzburd
Digitale Arithmetik Ercegovac Milos D., Lang Tomas
"Die Struktur und Interpretation von Computerprogrammen" Harold Abelson, Gerald Sassman

Siehe auch
Der Artikel "Zu einer Aufgabe, die im Interview nicht mehr angeboten wird."
Der Blog von Spice IT Recruitment veröffentlicht Interviewaufgaben für verschiedene Unternehmen.
Aufgaben für Interviews in Yandex.
In diesem Video löst A. Savvateev Probleme mit Interviews bei Tesla.