Wie sind technische Indikatoren an den Aktienmärkten?

Jeder, der sich jemals für Aktien- oder Kryptowährungsmärkte interessiert hat, hat diese zusätzlichen Zeilen gesehen. Und Sie haben wahrscheinlich Meinungen von erfahrenen Händlern gehört, dass sie nicht funktionieren und wie sie nichts verwenden. Aber sie helfen sehr und mein Handelsterminal, das ich mir einmal am Tag träge ansehe, sieht ungefähr so ​​aus wie auf dem Bild unten.

Wie sind sie alle gleich angeordnet? Und für wen kann das nützlich sein? Sie sollten sich auf jeden Fall damit vertraut machen, wenn:

1. Sie verwenden sie in Ihrem Handel
2. Planen Sie einen Handelsroboter zu schreiben?
3. Möchten Sie selbst eine Handelsstrategie umsetzen?

Ein technischer Indikator ist meistens eine Fenster-, Gewichts- oder Wiederholungsfunktion von Preisen und Mengen, die aus dem Austausch im Format einer Reihe von TOHLCV-Kerzen stammen (Unix-Zeit, offen, hoch, niedrig, geschlossen, Volumen). Verschiedene Filter, Maximum-Minimums oder andere Indikatoren können auch als Grundlage für nachfolgende Berechnungen verwendet werden.

Gleitender Durchschnitt (SMA)

Bei der Implementierung von Indikatoren ist es sehr praktisch, einen funktionalen Programmieransatz zu verwenden. Bei einem gleitenden Durchschnitt ist dies beispielsweise nur der Durchschnitt jedes Werts der Funktion für gleitende Fenster zum Schlusskurs

function sma($close, window) { return rolling(x => mean(x), window, $close); } 

Dabei ist die Funktion mean () der Durchschnittswert, der Fensterparameter die Fenstergröße und rolling () eine Kombination aus der Fensterfunktion, die für jede aktuelle Zelle im Array ein Array der letzten n Elemente erzeugt, und der Operation, die das Fenster auf eine Zahl minimiert.

 function rolling(operation, window, array) { let result = []; for (let i = 0; i < array.length; i++) { if (i + 1 < window) { result.push(NaN); } else { result.push(operation(array.slice(i + 1 - window, i + 1))); } } return result; } 

Der gleitende Durchschnitt ist ein nachlaufender Indikator und hilft bei der Bestimmung des Trends. Es wird über das Preisdiagramm gelegt und die ersten Werte werden normalerweise verworfen.



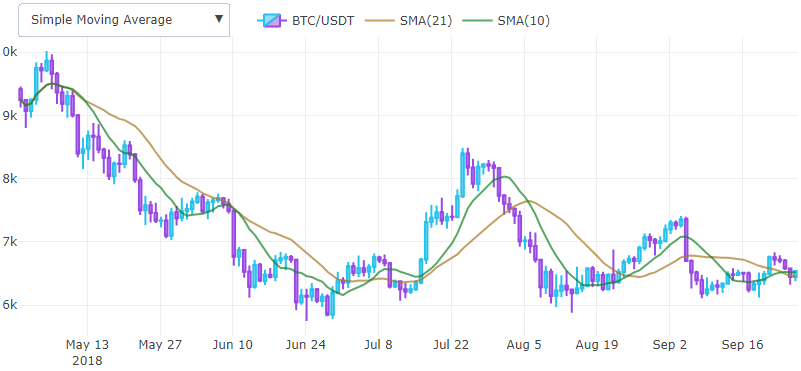
Normalerweise wird ein Indikatorpaar betrachtet, und der Punkt, an dem ein Indikator mit einem kurzen Fenster einen Indikator mit einem langen Fenster kreuzt, wird als potenzieller Eintrittspunkt von unten und als Austrittspunkt von oben betrachtet. In der Praxis wird häufiger ein exponentiell gewichteter gleitender Durchschnitt verwendet, wobei eine gewichtete Fensterfunktion verwendet wird, um den Verzögerungseffekt zu verringern.

Standardabweichung (STDEV)

Wenn wir die Funktion mean () in der vorherigen Version durch die Wurzel aus der Varianz sd () ersetzen, erhalten wir eine sich bewegende Standardabweichung.

 function stdev($close, window) { return rolling(x => sd(x), window, $close); } 

Die Dispersion wird auf übliche Weise als üblich angesehen, meistens ohne Bessel-Korrektur. Die Wurzel der Varianz wird ebenfalls verwendet, da die Varianz selbst in Quadrat Rubel / Dollar gemessen wird.

Bollinger Bands (BB)

Somit haben wir bereits zwei grundlegende Indikatoren erhalten, die bereits kombiniert werden können und neue erhalten. Wenn wir zum Beispiel den gleitenden Durchschnitt und die Standardabweichung Punkt für Punkt addieren und mit 2 multiplizieren, erhalten wir den oberen Teil des Bollinger-Bandes und subtrahieren den unteren Teil.



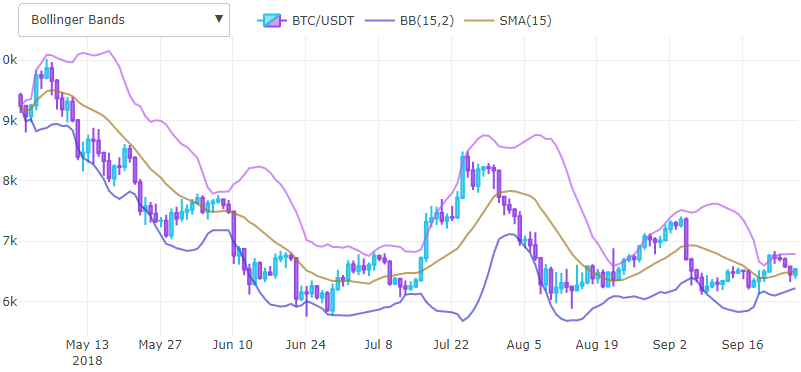
Im Code sieht es so aus

 function bb($close, window, mult) { let middle = sma($close, window); let upper = pointwise((a, b) => a + b * mult, middle, stdev($close, window)); let lower = pointwise((a, b) => a - b * mult, middle, stdev($close, window)); return { lower : lower, upper : upper}; } 

wobei die pointwise-Funktion nichts anderes tut, als ein Element aus zwei Arrays unter Verwendung der ihr zugewiesenen Operation zu sammeln.

Bollinger-Bänder helfen bei der Bestimmung der Flaute vor einer großen Preisbewegung und werden als Hilfsmittel zur bequemen Anzeige der Volatilität in einem Chart verwendet. Die Standardabweichung kann nicht als Überlagerung auf demselben Chart wie der Preis angezeigt werden. Daher ist es zweckmäßig, sie vom gleitenden Durchschnitt zu verschieben.



Exponentiell gewichteter gleitender Durchschnitt (EMA)

Wie kann die Verzögerung des gleitenden Durchschnitts verringert werden? Da bei der Berechnung n die letzten Schlusskurse addiert werden, können Sie verstehen, dass Sie mit etwas Gewicht addieren können, wodurch der Beitrag der alten Preise verringert wird. Damit kommen wir zur Formel für eine gewichtete Fensterfunktion.

$$

$$\ bar x = \ frac {\ sum x_i} {N} = \ frac {\ sum 1 \ cdot x_i} {\ sum 1} \ quad \ Rightarrow \ quad \ widetilde {x} = \ frac {\ sum x_i w_i } {\ sum w_i}$$

wenn $$$w_i = q ^ i$ und wählen Sie eine Art Konstante $$$q$ weniger als eins, dann bekommen wir ein unendlich abnehmendes Gewicht, wenn wir gleichzeitig die Preise ab dem neuesten addieren.



Die Berechnungen können stark vereinfacht werden, wenn der Beitrag der Schwänze nicht berücksichtigt wird. Durch Erweitern der Fenstergröße auf die volle Länge können Sie eine rekursive Definition erhalten.

$$

$$1 + q + q ^ 2 + ... + q ^ n \ underset {n \ to \ infty} {\ underset {q <0} {\ approx}} \ frac {1} {1-q} \\ \ mathrm {EMA} _ {curr} = \ frac {\ sum x_i q ^ i} {\ sum q ^ i} \ approx (1-q) \ sum x_i q ^ i \\ \ mathrm {EMA} _ {next } = \ frac {x_ {next} + q \ cdot \ sum x_i q ^ i} {1 + q \ cdot \ sum q ^ i} = (1-q) \ cdot \ left [x_ {next} + q \ cdot \ sum x_i q ^ i \ right] \\ \ mathrm {EMA} _ {next} = (1-q) \ cdot x_ {next} + q \ cdot \ mathrm {EMA} _ {curr}$$

Daher müssen wir einen Wert auswählen $$$\ alpha = 1-q$ als Glättungskonstante. Es kann gezeigt werden, dass, wenn Sie nehmen $$$\ alpha = 2 / (N + 1)$ Der Schwerpunkt der obigen EMA- und SMA-Gewichte wird gleich. Im Code sieht alles viel einfacher aus.

 function ema($close, window, weight = null) { weight = weight ? weight : 2 / (window + 1); let ema = [ mean($close.slice(0, window)) ]; for (let i = 1; i < $close.length; i++) { ema.push($close[i] * weight + ema[i - 1] * (1 - weight)); }; return ema; } 

Im Allgemeinen ist dies der gleiche gleitende Durchschnitt, jedoch empfindlicher.



Die Effizienz der Nutzung hängt von Ihrer Erfahrung und den verwendeten Einstellungen ab. Auf dieser Site sind die Parameter beispielsweise ziemlich gut ausgewählt.

Moving Average Convergence / Divergence (MACD)

Gerald Appel entwickelte 1979 einen der einfachsten und gleichzeitig effektivsten Oszillatoren von Preispunkten. Es wandelt zwei EMA-Trendindikatoren in einen Momentindikator um und holt das Beste aus zwei Welten. Das heißt, er findet grob gesagt eine Ableitung. Es wird in einem separaten Fenster mit zwei Linien und einem Histogramm gezeichnet und nicht wie die vorherigen überlagert. Tatsächlich gibt es viel mehr Indikatoren, die in einem separaten Fenster gezeichnet werden, aber dies kann zu einem anderen Zeitpunkt sein.



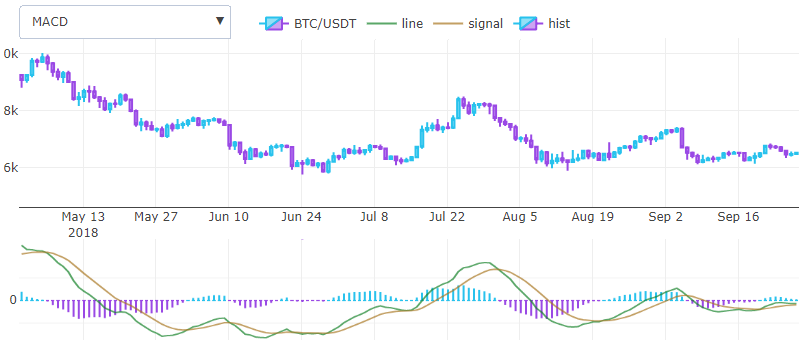
Die Berechnungsformel ist recht einfach: Nehmen Sie zwei Ema mit einem kurzen und einem kurzen Fenster, z. B. 26 und 12 Einheiten, und subtrahieren Sie die resultierende Linie als gewünschten Indikator. Nehmen wir ein weiteres Ema aus dieser Differenz mit einem Schritt von 3 Einheiten, erhalten wir eine Signalleitung. Das Histogramm, das Gerald später hinzufügte, wird aus der Differenz zwischen den beiden vorherigen Ergebnissen berechnet und ist im Wesentlichen eine gewichtete durchschnittliche Ableitung.

 function macd($close, wshort, wlong, wsig) { let line = pointwise((a, b) => a - b, ema($close, wshort), ema($close, wlong)); let signal = ema(line, wsig); let hist = pointwise((a, b) => a - b, line, signal); return { line : line, signal : signal, hist : hist }; } 

Indikatortest, normalisierter Standardfehler

Mit genauen Tabellen mit der Bedeutung von Indikatoren können Sie Ihre Berechnung qualitativ testen. Es gibt verschiedene Möglichkeiten, das Fehlermaß zwischen zwei Funktionen zu bestimmen, aber die Praxis hat gezeigt, dass der normalisierte mittlere quadratische Fehler, der als betrachtet wird

$$

$$\ mathrm {NRMSE} = \ left. \ sqrt {\ frac {\ sum (\ hat x_i - x_i) ^ 2} {N}} \ middle / (\ max {x_i} - \ min {x_i}) \ right.$$

funktioniert am besten für kleine und große Größen. Zum Beispiel kann Bitcoin in Dollar 20.000 US-Dollar kosten und die Differenz von 10 US-Dollar ist nicht kritisch. Gleichzeitig kann eine Altmünze in mehreren Satoshi berechnet werden.

 function nrmse(f, g) { let sqrDiff = pointwise((a, b) => (a - b) * (a - b), f, g); return Math.sqrt(mean(sqrDiff)) / (Math.max(...f) - Math.min(...f)); } 

Fazit

In wenigen Zeilen können Sie also die Basisindikatoren ausdrücken. Wenn Sie vorhaben, ihre Analyse durch maschinelles Lernen durchzuführen und dann die idealen Einstiegspunkte zu bestimmen, empfehle ich Ihnen, auf den ZigZag-Indikator zu achten, der für den Handel nicht nützlich, aber als Lehrer äußerst nützlich ist. Es sollte auch berücksichtigt werden, dass Sie für den Handel die unterschiedlichsten Indikatoren auswählen und versuchen müssen, deren Eingabeparameter zu ändern. Sie können versuchen, sie im Laufe der Zeit automatisch zu ändern, da sich die effektivsten Parameter tendenziell ändern.

Verwendete Quellen

1. StockCharts - Liste der Algorithmen mit Verifizierungsdaten in Tabellen
2. Cryptowatch - gut abgestimmte Indikatorparameter
3. Github - Quellcode