Um die Erkennung durch feindliche Radargeräte zu vermeiden, sollten moderne Jäger, Schiffe und Raketen die kleinste effektive Ausbreitungsfläche (EPR) haben. Wissenschaftler und Ingenieure, die solche unauffälligen Objekte mithilfe von Methoden der rechnergestützten Elektrodynamik entwickeln, optimieren den EPR und die Streueffekte beliebiger Objekte bei Verwendung von Radargeräten. Das fragliche Objekt streut die auf es einfallenden elektromagnetischen Wellen in alle Richtungen, und ein Teil der Energie wird dabei als Quelle sogenannter elektromagnetischer Wellen zurückgegeben Rückstreuung bildet eine Art "Echo" des Objekts. EPR ist nur ein Maß für die Intensität eines Radarechosignals.

In der Praxis wird eine leitfähige Referenzkugel als Objekt zum Kalibrieren von Radaren verwendet. Eine ähnliche Formulierung des Problems wird verwendet, um die numerische Berechnung des EPR zu verifizieren, da die Lösung für dieses klassische Problem der Elektrodynamik 1908 von Gustav Mi erhalten wurde .

In diesem Hinweis werden wir über die Durchführung einer solchen Referenzberechnung unter Verwendung einer effektiven zweidimensionalen achsensymmetrischen Formulierung sprechen und kurz die allgemeinen Prinzipien zur Lösung einer breiten Klasse von Streuproblemen in COMSOL Multiphysics ^® erwähnen.

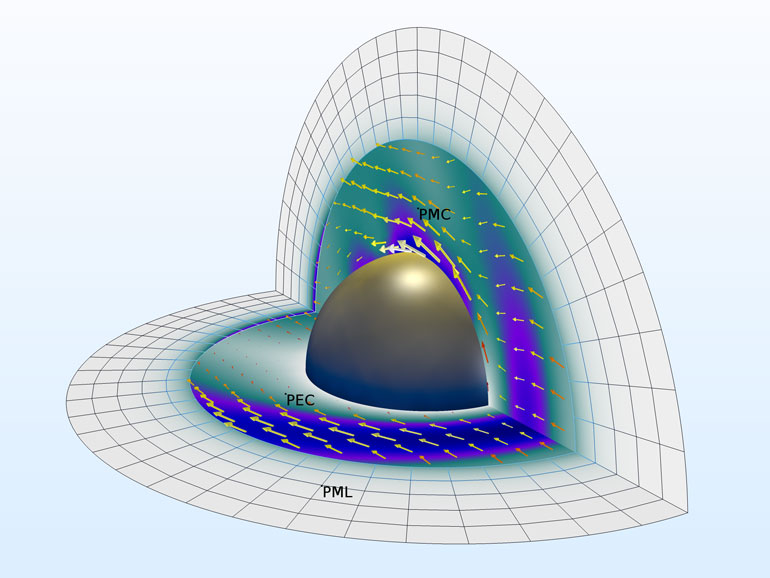
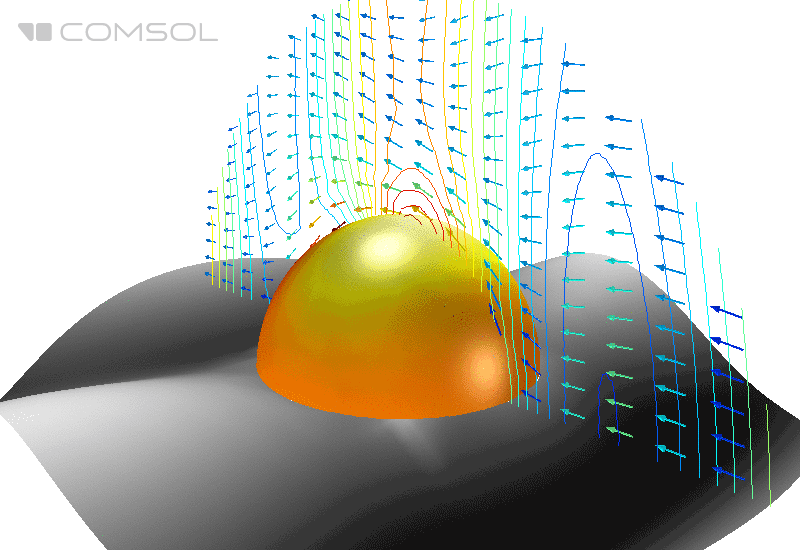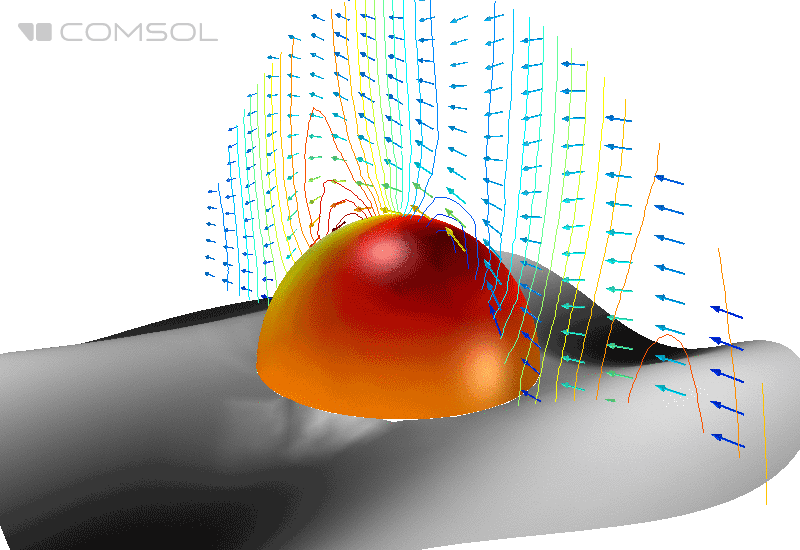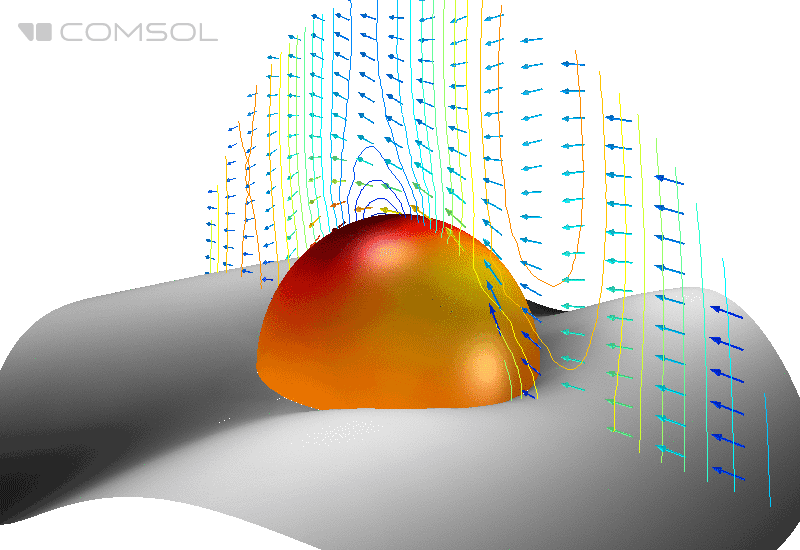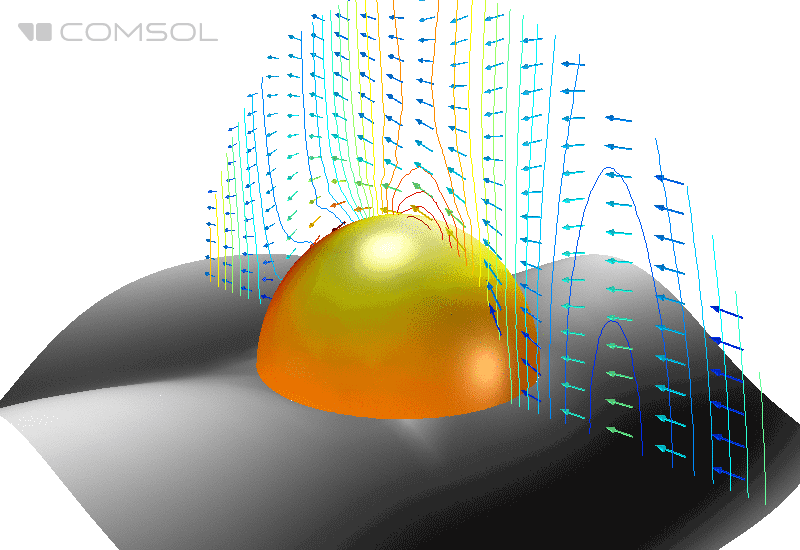
Abb. 1. Verteilung des elektrischen Feldes (seiner Norm) und des zeitlich gemittelten Energieflusses (Pfeile) um eine perfekt leitende Kugel im freien Raum.

Leitende Kugelstreuung: Größe ist wichtig

Im klassischen Referenzbeispiel wird eine perfekt leitende Metallkugel im freien Raum mit einer ebenen elektromagnetischen Welle bestrahlt und der EPR berechnet.

Am Ausgang wird die Streuung in der Regel für verschiedene Verhältnisse des Radius der Kugel und der Wellenlänge berechnet, anhand derer drei Bereiche unterschieden werden: das Rayleigh- , das optische und das Übergangs-Mi-Band.

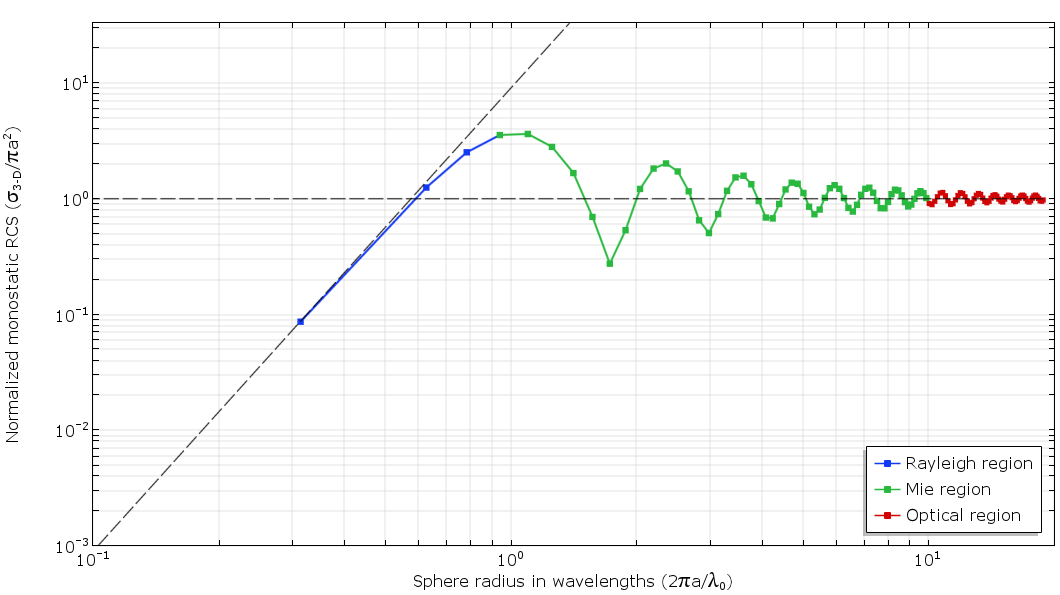
Abb. 2. Ein Diagramm der Abhängigkeit des EPR von der Wellenlänge (auf einer doppelten logarithmischen Skala). Es werden drei charakteristische Bereiche unterschieden: Rayleigh, Mi und Optisch. Schwarze gepunktete Linien zeigen asymptotische Lösungen für die Rayleigh- und optischen Zonen.

Die EPR-Eigenschaften werden erheblich von der elektrischen Größe und den Materialeigenschaften des Objekts beeinflusst, auf das der Radarstrahl fällt. Da die elektrische Größe des Objekts - in unserem Fall die Kugel - beim Übergang vom optischen Bereich zum Rayleigh-Bereich (über das M-Band) abnimmt, bieten asymptotische Methoden keine ausreichende Genauigkeit, um den Beitrag aller physikalischen Phänomene zu berücksichtigen. Um genaue Ergebnisse zu erhalten, sollte das Problem mithilfe von Vollwellentechniken gelöst werden.

In einer dreidimensionalen Umgebung kann selbst unter Berücksichtigung der Verwendung perfekt angepasster Schichten (Perfectly Matched Layers - PML), die den Rechenbereich effektiv einschränken und offene Grenzen und Symmetriebedingungen simulieren, eine Berechnung mit detaillierter Auflösung in Frequenz / Wellenlänge eine Weile dauern.

Einstellen der Symmetriebedingungen für elektrodynamische Berechnungen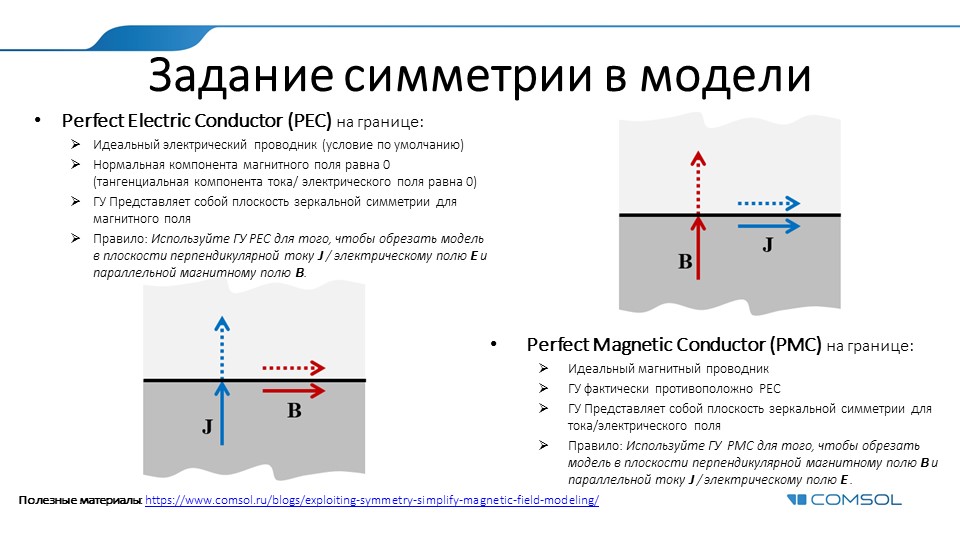

Weitere Details hier .

Glücklicherweise ist keine vollständige 3D-Analyse erforderlich, wenn das Objekt achsensymmetrisch ist und die Wellen isotrop streut. Um die Ausbreitung elektromagnetischer Wellen und das Resonanzverhalten eines Objekts zu analysieren, reicht es aus, unter bestimmten Bedingungen seinen Querschnitt in einer zweidimensionalen achsensymmetrischen Formulierung zu berechnen.

Zweidimensionales achsensymmetrisches Modell des Mikrowellenprozesses: ein Einblick

Angenommen, unsere Kugel ist metallisch und hat eine hohe Leitfähigkeit. Für diese Aufgabe wird die Oberfläche der Kugel als perfekter elektrischer Leiter (Perfect Electric Conductor - PEC) festgelegt und ihr innerer Teil vom Berechnungsbereich ausgeschlossen. Der Bereich um ihn herum wird als Vakuum mit den entsprechenden Materialeigenschaften definiert, und die kugelförmige PML wird in der äußersten Schicht verwendet, die verwendet wird, um alle ausgehenden Wellen zu absorbieren und eine Reflexion an den Grenzen des Rechenbereichs zu verhindern.

Modellierung von Metallobjekten bei elektromagnetischen Wellenproblemen

Für die numerische Lösung von Problemen der Elektrodynamik im Frequenzbereich gibt es verschiedene Methoden zur effizienten Modellierung von Metallobjekten. Die folgende Abbildung zeigt Techniken und Empfehlungen für die Verwendung der Bedingungen für die Übergangsgrenzbedingung (TBC), die Impedanzgrenzbedingung (IBC) und den perfekten elektrischen Leiter (PEC).

Eine detaillierte Analyse der Anwendungsaspekte von jedem von ihnen finden Sie hier .

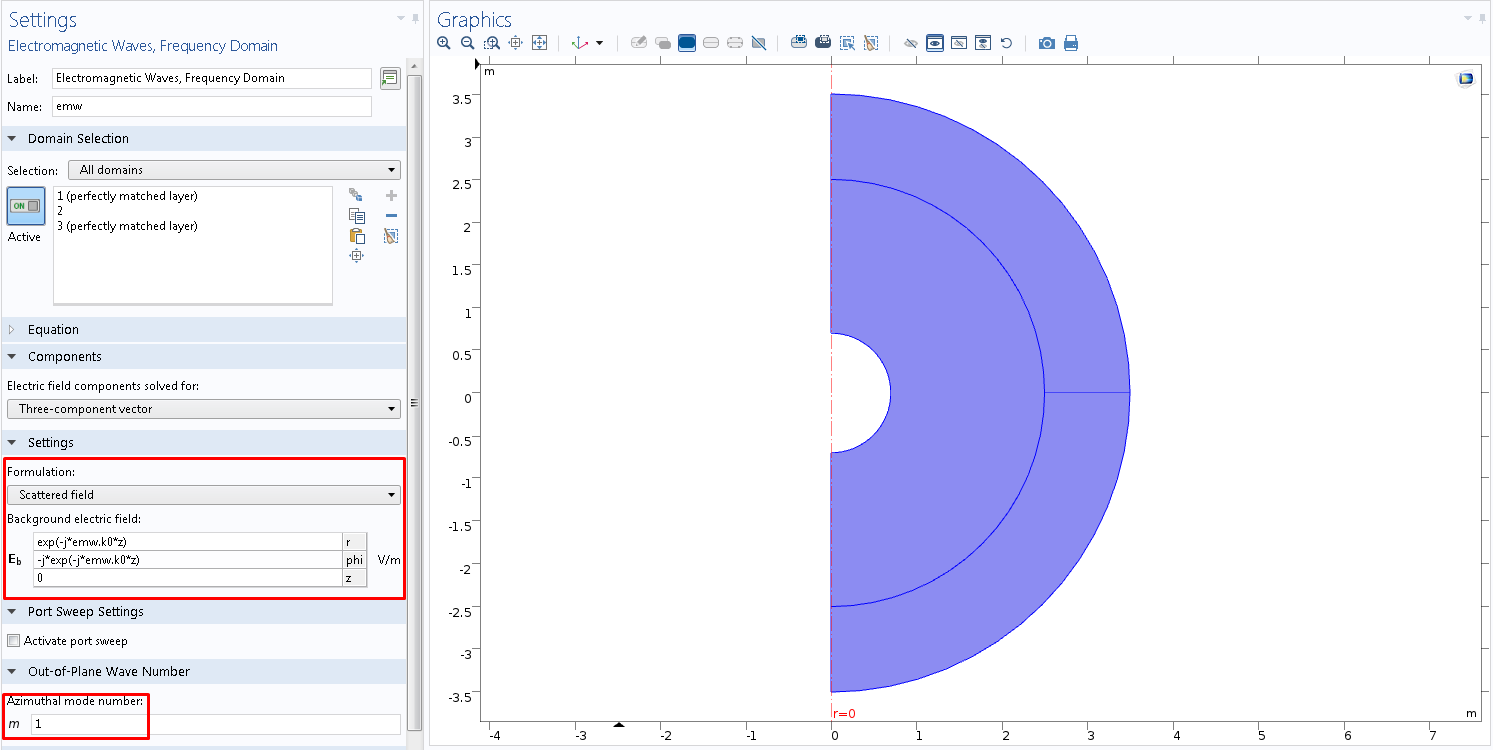
Abb. 3. Geometrie für die achsensymmetrische Formulierung und Einstellung des elektromagnetischen Hintergrundfelds mit linker Zirkularpolarisation in der grafischen Oberfläche von COMSOL Multiphysics ^® .

Im Rechenbereich (mit Ausnahme von PML) wird die Anregung des Hintergrundfeldes mit der linken Zirkularpolarisation in negativer Richtung der z-Achse angegeben (Abb. 3). Bitte beachten Sie, dass die Berechnung nur für den ersten Azimutmodus eingestellt ist.

Standardmäßig wird für Mikrowellenaufgaben in COMSOL Multiphysics ^® automatisch ^ein freies Dreiecksgitter (oder Tetraeder für 3D-Probleme) für die maximale Frequenz erstellt, die für die Studie im Frequenzbereich (Frequenzbereichsstudie) angegeben wurde, in diesem Beispiel 200 MHz. Um eine ausreichende Auflösung der Wellenprozesse im Modell sicherzustellen, wird die maximale Maschenelementgröße auf 0,2 Wellenlänge eingestellt. Mit anderen Worten wird die räumliche Auflösung als fünf Elemente zweiter Ordnung pro Wellenlänge angegeben. In perfekt aufeinander abgestimmten Schichten wird das Gitter durch Ziehen in Absorptionsrichtung aufgebaut, was eine maximale PML-Leistung gewährleistet.

Weil Da die Anzahl der Freiheitsgrade im Modell sehr gering ist (im Vergleich zur dreidimensionalen Formulierung), dauert die Berechnung nur wenige Sekunden. Am Ausgang kann der Benutzer die Verteilung des elektrischen Feldes um die Kugel (in der Nahzone) erhalten und visualisieren, die die Summe aus Hintergrund- und Streufeldern ist.

Für diese Aufgabe beziehen sich die interessantesten Eigenschaften auf die Fernfeldregion. Um sie in das Modell aufzunehmen, müssen Sie die Fernfeldberechnungsbedingung an der Außengrenze der Berechnungsdomäne (in diesem Fall die innere PML-Grenze) aktivieren, mit der Sie Felder in der Fernzone außerhalb der Berechnungsdomäne an jedem Punkt basierend auf den Stratton-Chu-Integralbeziehungen berechnen können. Durch die Aktivierung wird eine zusätzliche Variable hinzugefügt - die Feldamplitude in der Fernzone, auf deren Grundlage die Software bei der Nachbearbeitung technische Variablen berechnet, die den IEEE-Standards entsprechen: effektive isotrop abgestrahlte Leistung, Verstärkung (sogenannte Verstärkung, einschließlich Berücksichtigung der Eingangsfehlanpassung), Koeffizient Richtungsaktion und EPR.

Gemäß dem Polardiagramm kann ein Spezialist die Richtwirkung des Feldes in der Fernzone in einer bestimmten Ebene bestimmen, und ein dreidimensionales Strahlungsmuster in der Fernzone ermöglicht eine detailliertere Untersuchung des Streufelds (Abbildung 4).

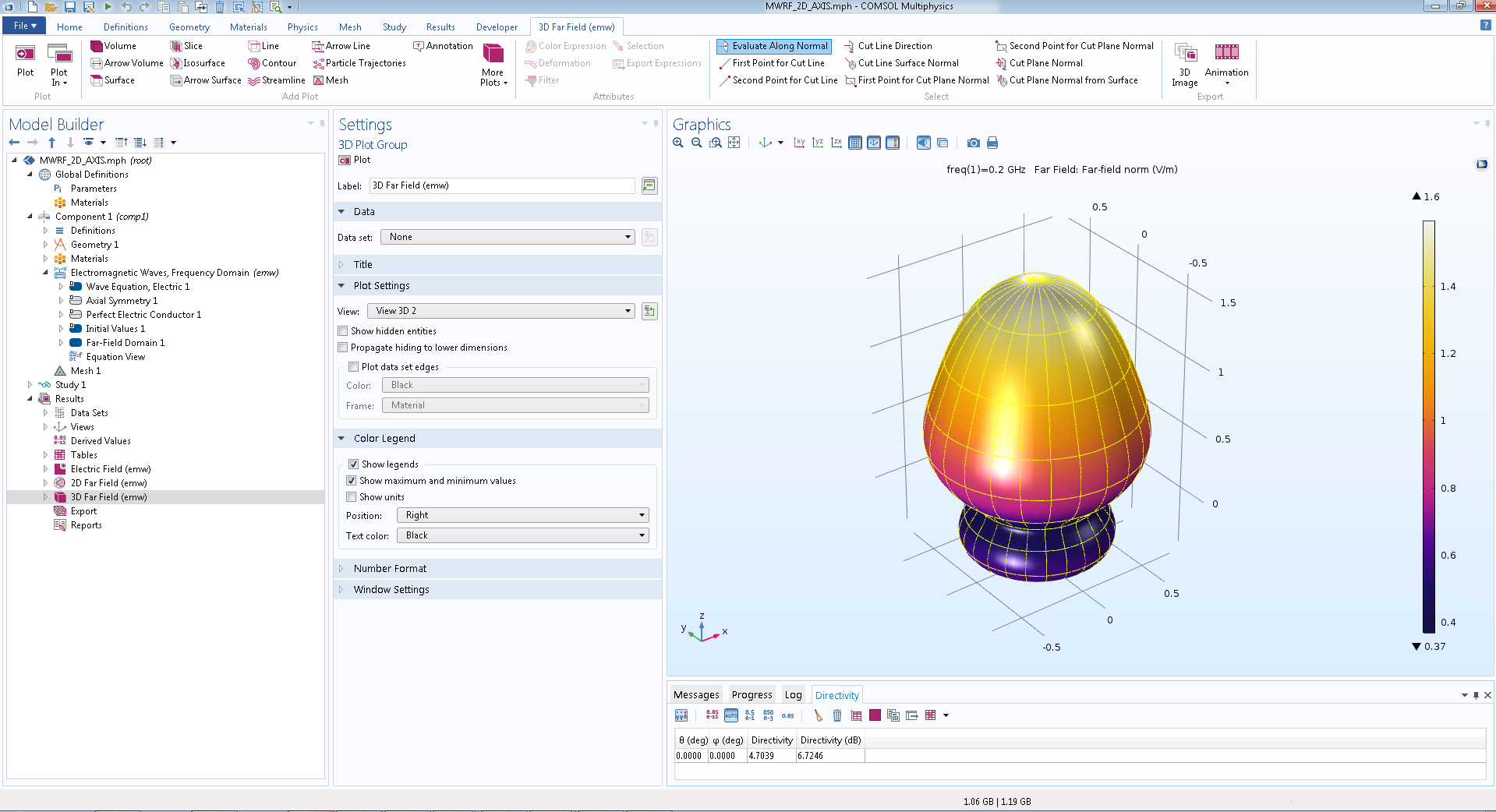
Abb. 4. Dreidimensionale Feldvisualisierung in der Fernzone basierend auf einem zweidimensionalen achsensymmetrischen Modell in COMSOL Multiphysics ^® .

Lösungswiederherstellung für ein dreidimensionales Problem

Die Ergebnisse für das "verkürzte" Modell in einer achsensymmetrischen Formulierung beziehen sich auf den Prozess der Bestrahlung der leitenden Kugel mit einem zirkular polarisierten Hintergrundfeld. In dem ursprünglichen 3d-Problem werden die Eigenschaften des Streufeldes für den Fall einer linear polarisierten ebenen Welle untersucht. Wie kann man diesen Unterschied umgehen?

Per Definition kann eine lineare Polarisation durch Hinzufügen der rechten und linken Zirkularpolarisation erhalten werden. Das zweidimensionale achsensymmetrische Modell mit den obigen Einstellungen (Abb. 2) entspricht dem ersten Azimutmodus (m = 1) des Hintergrundfeldes mit linker Zirkularpolarisation. Die Lösung für den negativen Azimutmodus mit rechter Zirkularpolarisation kann leicht aus dem bereits gelösten Problem abgeleitet werden, indem die Symmetrieeigenschaften verwendet und einfache algebraische Transformationen durchgeführt werden.

Nachdem Sie nur eine zweidimensionale Analyse durchgeführt und die Ergebnisse gespiegelt haben, die sich bereits in der Nachbearbeitung befinden, können Sie alle erforderlichen Daten extrahieren und so Rechenaufwand erheblich sparen (Abb. 5).

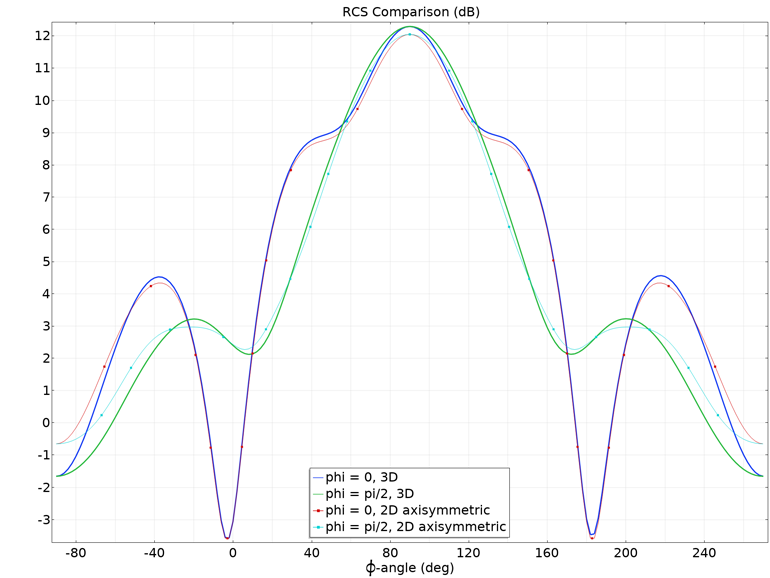
Abb. 5. Vergleich des Sweeps der effektiven Streufläche (auf einer logarithmischen Skala) über Streuwinkel für eine vollständige dreidimensionale Berechnung und das vorgeschlagene zweidimensionale achsensymmetrische Modell.

Der eindimensionale Graph (Fig. 5) mit einem EPR-Vergleich zeigt eine akzeptable Entsprechung zwischen dem dreidimensionalen und dem zweidimensionalen achsensymmetrischen Modell. Eine leichte Diskrepanz wird nur im Bereich der Vorwärts- und Rückwärtsstreuung nahe der Rotationsachse beobachtet.

Zusätzlich ist zur Visualisierung der erhaltenen zweidimensionalen Ergebnisse im dreidimensionalen Raum eine Transformation des Koordinatensystems von zylindrisch nach kartesisch erforderlich. In Abb. Abbildung 6 zeigt eine dreidimensionale Visualisierung der Ergebnisse für ein zweidimensionales achsensymmetrisches Modell.

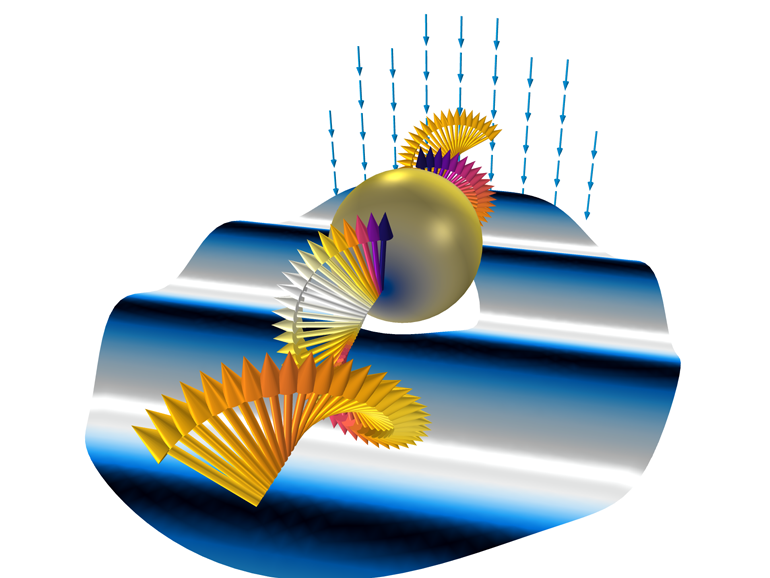
Abb. 6. Dreidimensionale Darstellung der Ergebnisse basierend auf zweidimensionaler Berechnung.

In einer Spirale rotierende Pfeile zeigen ein Hintergrundfeld mit zirkularer Polarisation an. Das Diagramm im horizontalen Schnitt zeigt die Verteilung der radialen Komponente des Hintergrundfelds (der Wellenprozess wird anhand von Verformungen der Ebene angezeigt). Die Norm des gesamten elektrischen Feldes ist auf der Oberfläche der Kugel aufgebaut. Ein weiteres Pfeildiagramm zeigt eine Überlagerung zweier zirkularer Polarisationen, die einem Hintergrundfeld mit linearer Polarisation im dreidimensionalen Raum entspricht.

Fazit

Im Zuge der modernen Entwicklung auf dem Gebiet der Radiophysik und Mikrowellentechnologie für Ingenieure sind effektive Modellierungstechniken, die den Ressourcen- und Zeitverbrauch reduzieren, unabhängig von der angewandten Methode der numerischen Analyse unersetzlich.

Um die Integrität zu erhalten und alle relevanten physikalischen Effekte bei der Modellierung einer realen Komponente mit einer großen elektrischen Größe wiederherzustellen, ist es möglich, den Prozess der numerischen Berechnung ohne Genauigkeitsverlust zu vereinfachen, indem das Problem in einer zweidimensionalen achsensymmetrischen Formulierung gelöst wird. Bei der Modellierung und Analyse von achsensymmetrischen Objekten wie Streukugeln und -scheiben, konischem Horn und Parabolantennen werden Berechnungen für den Gerätequerschnitt mehrere Größenordnungen schneller durchgeführt als bei Verwendung des vollständigen dreidimensionalen Modells.

Grundlagen der Antennenmodellierung in der COMSOL-Multiphysik

Eine kurze Videoübersicht (in russischer Sprache) , die Beispiele für die Modellierung von Mikrowellenantennen mithilfe des Hochfrequenzmoduls zeigt, einschließlich der Berechnung der Frequenzcharakteristik von S-Parametern und Impedanz, Smith-Diagrammen, Übereinstimmungsstudien, Berechnung von Feldern in der Fernzone und Bestimmung des Richtungskoeffizienten (Richtwirkung) und gewinnen (gewinnen). Darüber hinaus werden die Prinzipien der Verwendung von Symmetrie, die Modellierung von Antennen beim Empfang und komplexe Berechnungen von Systemen von Empfängern und Sendern im Raum, die Bewertung elektromagnetischer Interferenzen mit benachbarten Antennen und vieles mehr berücksichtigt.

In diesem Fall ermöglicht eine einfache zweidimensionale Formulierung eine schnelle Rekonstruktion im dreidimensionalen Raum und eine Untersuchung der Streuung des Hintergrundfeldes mit linearer Polarisation sowie der Richtwirkung der Strahlung in der Fernzone für Antennen, die durch den transversalen TE11-Kreiswellenleiter angeregt werden.

Weitere Informationen

Dieses Material basiert auf einem Artikel von J. Munn. Schnelle numerische Analyse von Streuung und Radarquerschnitt , Mikrowellen & HF 3. Mai 2018

Mit der COMSOL Multiphsycics ^® -Funktion können Sie außerdem Folgendes simulieren:

• Freiformradargeräte und Radargeräte
• Breitbandstreuung basierend auf der DG-FEM-Technik (Zeitbereichsformulierung unter Verwendung expliziter Löser und anschließende FFT-Umwandlung)
• Streuung durch 3D-Objekte, insbesondere durch ein auf einem dielektrischen Substrat angeordnetes Nanopartikel .

Um die Funktionen unseres Pakets für die in diesem Artikel behandelten Anwendungen genauer kennenzulernen , laden wir Sie ein, an unserem neuen Webinar "Lösung von Streuproblemen in COMSOL Multiphsycics ^® " teilzunehmen , das am 22. August 2018 stattfinden wird.

Sie können auch eine Demoversion von COMSOL in den Kommentaren oder auf unserer Website anfordern.

Endgültiges GIF: