Numerische Methoden zur Lösung nichtlinearer Gleichungssysteme

Einführung

Viele angewandte Probleme führen dazu, dass eine allgemeine Lösung für ein System nichtlinearer Gleichungen gefunden werden muss. Es wurde keine allgemeine analytische Lösung des Systems nichtlinearer Gleichungen gefunden. Es gibt nur numerische Methoden.

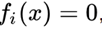
Es sollte eine interessante Tatsache beachtet werden, dass jedes Gleichungssystem über reelle Zahlen durch eine äquivalente Gleichung dargestellt werden kann, wenn wir alle Gleichungen in der Form nehmen , quadriere sie und falte sie.

Für die numerische Lösung werden iterative Methoden aufeinanderfolgender Approximationen (einfache Iteration) und die Newtonsche Methode in verschiedenen Modifikationen verwendet. Iterative Prozesse werden natürlich auf den Fall eines Systems nichtlinearer Gleichungen der Form verallgemeinert:

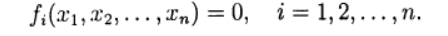
(1)

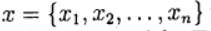
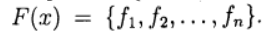
Bezeichnen mit Vektor von Unbekannten und definieren Sie eine Vektorfunktion Dann wird System (1) in Form der Gleichung geschrieben:

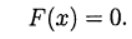
(2)

Kehren wir nun zu unserem geliebten Python zurück und stellen dessen Vorrang unter den Programmiersprachen fest, die lernen möchten [1].



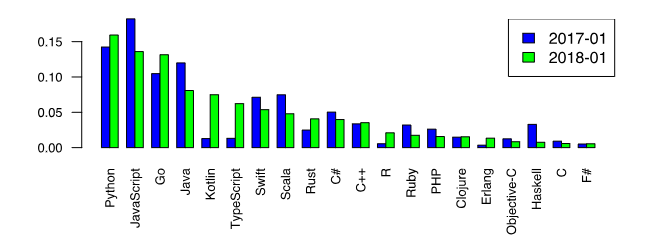
Diese Tatsache ist ein zusätzlicher Anreiz, numerische Methoden in Python in Betracht zu ziehen. Python-Liebhaber sind jedoch der Meinung, dass spezielle Bibliotheksfunktionen wie scipy.optimize.root, spsolve_trianular und newton_krylov die beste Wahl sind, um Probleme mit numerischen Methoden zu lösen.

Es ist schwer, dem zu widersprechen, schon allein deshalb, weil die Vielfalt der Module Python zu einem Höhepunkt der Popularität gemacht hat. Es gibt jedoch Fälle, in denen auch bei einer flüchtigen Prüfung die Verwendung direkt bekannter Methoden ohne Verwendung spezieller Funktionen der SciPy-Bibliothek ebenfalls gute Ergebnisse liefert. Mit anderen Worten, das Neue ist das gut vergessene Alte.

In der Veröffentlichung [2] wurde anhand von Computerexperimenten nachgewiesen, dass die Bibliotheksfunktion newton_krylov, die zur Lösung großer nichtlinearer Gleichungssysteme entwickelt wurde, halb so schnell ist wie der TSLS + WD-Algorithmus
(zweistufige kleinste Quadrate), implementiert von der NumPy-Bibliothek.

Der Zweck dieser Veröffentlichung ist es, die Anzahl der Iterationen, die Geschwindigkeit und vor allem das Ergebnis der Lösung eines Modellproblems in Form eines Systems von einhundert nichtlinearen algebraischen Gleichungen mit der Bibliotheksfunktion scipy.optimize.root und der mit der NumPy-Bibliothek implementierten Newton-Methode zu vergleichen.

Scipy.optimize.root-Solver-Funktionen zum numerischen Lösen von Systemen algebraischer nichtlinearer Gleichungen

Die Bibliotheksfunktion scipy.optimize.root wurde als Vergleichsbasis gewählt, da sie über eine umfangreiche Bibliothek von Methoden verfügt, die für die vergleichende Analyse geeignet sind.

scipy.optimize.root ( fun, x0, args = (), method = 'hybr', jac = None, tol = None, callback = None, ptions = None )
fun - Eine Vektorfunktion zum Finden der Wurzel.
x0 - Anfangsbedingungen für das Finden von Wurzeln

Methode:
Es wird eine Hybr- Powell-Modifikation der Hybridmethode verwendet.
lm - löst nichtlineare Gleichungssysteme mit der Methode der kleinsten Quadrate.
Wie aus der Dokumentation [3] hervorgeht, sind die Methoden broyden1, broyden2, anderson, lineares Mischen, Diagbroyden, aufregendes Mischen, Krylov die genauen Newtonschen Methoden. Die übrigen Parameter sind „optional“ und finden Sie in der Dokumentation.

Methoden zur Lösung nichtlinearer Gleichungssysteme

Das unten angegebene Material kann zwar in der Literatur gelesen werden, zum Beispiel in [4], aber ich respektiere meinen Leser und präsentiere die Ableitung der Methode, wenn möglich, wenn möglich in gekürzter Form. Diejenigen, die keine Formeln mögen, überspringen diesen Abschnitt.

Bei der Newtonschen Methode wird aus der Lösung des linearen Gleichungssystems eine neue Näherung zur Lösung des Gleichungssystems (2) ermittelt:

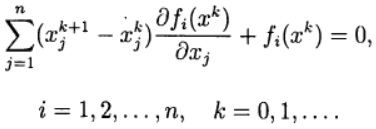
(3)

Definieren Sie die Jacobi-Matrix:

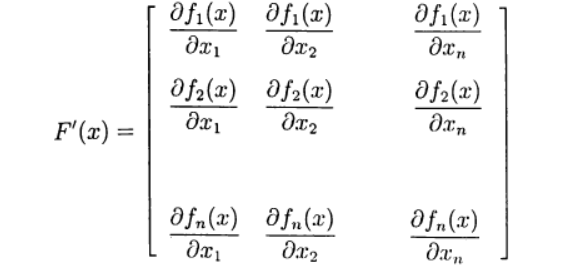
(4)

Wir schreiben (3) in der Form:

(5)

Viele Ein-Schritt-Methoden zur ungefähren Lösung von (2) in Analogie zu zweischichtigen iterativen Methoden zur Lösung von Systemen linearer algebraischer Gleichungen können in folgender Form geschrieben werden:

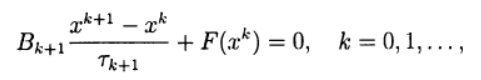
(6)

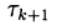
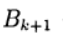
wo Sind iterative Parameter, a - eine quadratische Matrix n x n mit der Umkehrung.

Bei Verwendung des Datensatzes (6) entspricht Newtons Methode (5) der Auswahl:



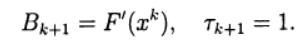
Das System der linearen Gleichungen (5) zum Finden einer neuen Näherung kann iterativ gelöst werden. In diesem Fall haben wir einen zweistufigen iterativen Prozess mit externen und internen Iterationen. Beispielsweise kann ein externer iterativer Prozess gemäß der Newton-Methode ausgeführt werden, und interne Iterationen können auf der Basis der iterativen Seidel-Methode ausgeführt werden.

Beim Lösen nichtlinearer Gleichungssysteme können direkte Analoga von iterativen Standardmethoden verwendet werden, die zum Lösen linearer Gleichungssysteme verwendet werden. Die nichtlineare Seidel-Methode, wie sie auf Lösung (2) angewendet wird, ergibt:

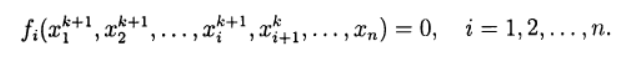
(7)

In diesem Fall kann jede Komponente der neuen Näherung aus der Lösung der nichtlinearen Gleichung auf der Basis der einfachen Iterationsmethode und der Newtonschen Methode in verschiedenen Modifikationen erhalten werden. Wir kommen also wieder zu einer zweistufigen iterativen Methode, bei der externe Iterationen gemäß der Seidel-Methode und interne Iterationen mit der Newton-Methode durchgeführt werden.

Die Hauptberechnungsschwierigkeiten bei der Anwendung der Newton-Methode für die ungefähre Lösung nichtlinearer Gleichungssysteme hängen mit der Notwendigkeit zusammen, bei jeder Iteration ein lineares Gleichungssystem mit einer Jacobi-Matrix zu lösen , und diese Matrix ändert sich von Iteration zu Iteration. Bei der modifizierten Newton-Methode wird die Jacobi-Matrix nur einmal invertiert:

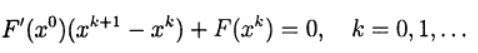
(8)

Auswahl der Modellfunktion

Eine solche Wahl ist keine einfache Aufgabe, da sich mit einer Zunahme der Anzahl von Gleichungen im System entsprechend einer Zunahme der Anzahl von Variablen das Ergebnis der Lösung nicht ändern sollte, da es sonst unmöglich ist, die Richtigkeit der Lösung des Gleichungssystems beim Vergleich zweier Methoden zu verfolgen. Ich bringe die folgende Lösung für die Modellfunktion:

n=100 def f(x): f = zeros([n]) for i in arange(0,n-1,1): f[i] = (3 + 2*x[i])*x[i] - x[i-1] - 2*x[i+1] - 2 f [0] = (3 + 2*x[0] )*x[0] - 2*x[1] - 3 f[n-1] = (3 + 2*x[n-1] )*x[n-1] - x[n-2] - 4 return f 

Die Funktion f erzeugt ein System von n nichtlinearen Gleichungen, deren Lösung nicht von der Anzahl der Gleichungen abhängt und für jede der n Variablen gleich Eins ist.

Ein Programm zum Testen einer Modellfunktion mit den Ergebnissen der Lösung eines Systems algebraischer nichtlinearer Gleichungen unter Verwendung der Bibliotheksfunktion optimize.root für verschiedene Methoden zum Finden von Wurzeln

 from numpy import* from scipy import optimize import time ti = time.clock() n=100 def f(x): f = zeros([n]) for i in arange(0,n-1,1): f[i] = (3 + 2*x[i])*x[i] - x[i-1] - 2*x[i+1] - 2 f [0] = (3 + 2*x[0] )*x[0] - 2*x[1] - 3 f[n-1] = (3 + 2*x[n-1] )*x[n-1] - x[n-2] - 4 return f x0 =zeros([n]) sol = optimize.root(f,x0, method='krylov') print('Solution:\n', sol.x) print('Krylov method iteration = ',sol.nit) print('Optimize root time', round(time.clock()-ti,3), 'seconds') 

Nur eine der in der Dokumentation [3] angegebenen Methoden hat die Prüfung des Ergebnisses der Lösung einer Modellfunktion bestanden. Dies ist die 'krylov'-Methode .

Lösung für n = 100:

Lösung:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1.]
Iteration der Krylov-Methode = 4219
Optimieren Sie die Root-Zeit auf 7,239 Sekunden:


Schlussfolgerung: Bei einer Erhöhung der Anzahl der Gleichungen um den Faktor zwei macht sich das Auftreten von Fehlern in der Lösung bemerkbar. Mit einem weiteren Anstieg von n wird die Lösung inakzeptabel, was aufgrund der automatischen Anpassung an den Schritt möglich ist, der gleiche Grund für einen starken Leistungsabfall. Aber das ist nur meine Vermutung.

Ein Programm zum Testen einer Modellfunktion mit den Ergebnissen der Lösung eines Systems algebraischer nichtlinearer Gleichungen unter Verwendung eines in Python 3 geschriebenen Programms unter Berücksichtigung der Beziehungen (1) - (8), um die Wurzeln unter Verwendung der modifizierten Newton-Methode zu finden

Lösung für n = 100:

Lösung:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1.]
Newton-Iteration = 13
Newton-Methodenzeit 0,496 Sekunden

Lösung für n = 200:

Lösung:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1.]
Newton-Iteration = 14
Newton-Methodenzeit 1,869 Sekunden

Um sicherzustellen, dass das Programm das System wirklich löst, schreiben wir die Modellfunktion zum Vermeiden der Wurzel mit dem Wert 1 in der folgenden Form neu:

 n=10 def f(x): f = zeros([n]) for i in arange(0,n-1,1): f[i] = (3 + 2*x[i])*x[i]*sin([i]) - x[i-1] - 2*x[i+1] - 2+e**-x[i] f [0] = (3 + 2*x[0] )*x[0] - 2*x[1] - 3 f[n-1] = (3 + 2*x[n-1] )*x[n-1] - x[n-2] - 4 return f 

Wir bekommen:
Lösung:
[0.96472166 0.87777036 0.48175823 -0.26190496 -0.63693762 0.49232062
-1,31649896 0,6865098 0,89609091 0,98509235]
Newton-Iteration = 16
Newton-Methodenzeit 0,046 Sekunden

Fazit: Das Programm funktioniert auch, wenn sich die Modellfunktion ändert.

Nun kehren wir zur ursprünglichen Modellfunktion zurück und überprüfen einen größeren Bereich für n, beispielsweise bei 2 und 500.
n = 2
Lösung:
[1. 1.]
Newton-Iteration = 6
Newton-Methodenzeit 0,048 Sekunden
n = 500

Schlussfolgerungen:

Ein in Python unter Verwendung der modifizierten Newton-Methode geschriebenes Programm hat beim Lösen von nichtlinearen Gleichungssystemen aus der gegebenen Modellfunktion eine höhere Lösungsstabilität als beim Lösen mit der Bibliotheksfunktion optimize.root (f, x0, method = 'krylov') für die Krylov-Methode. In Bezug auf die Geschwindigkeit der endgültigen Schlussfolgerung ist es aufgrund des unterschiedlichen Ansatzes zur Schrittsteuerung unmöglich zu zeichnen.

Referenzen:

1. Bewertung der Programmiersprachen 2018.
2. Cooper I.V., Faleychik B.V. Nichtmatrix-iterative Prozesse mit Unterdrückung des quadratischen mittleren Fehlers für große Systeme nichtlinearer Gleichungen.
3. scipy.optimize.root.
4. Vabishchevich P.N. Numerische Methoden: Computerworkshop. - M.: Buchhaus "LIBROCOM", 2010. - 320 p.