Ist eine sofortige Übertragung von Informationen möglich? Quantenverschränkte Teilchenexperimente

Guten Tag an alle!
Wir betrachten weiterhin die Möglichkeiten der Quantenmechanik zur Informationsübertragung unter Verwendung der Korrelation von quantenverschränkten Teilchen. Im Gegensatz zu klassischen Kommunikationsmethoden bietet die Verwendung von quantenverschränkten Partikeln die Möglichkeit, Informationen sofort über große Entfernungen zu übertragen. Die Schwierigkeit besteht darin, Wege zu finden, um die übertragenen Informationen zu codieren und zu decodieren. Dieser Artikel befasst sich mit der Suche nach Lösungen für dieses Problem und der Möglichkeit, einen Versuchsaufbau zu erstellen. Wenn Sie auch an dieser Aufgabe interessiert sind - willkommen bei cat!

Ich möchte Sie daran erinnern, dass wir im letzten Artikel eines der möglichen Schemata für die Übertragung von Informationen zwischen zwei entfernten Objekten betrachtet haben. Insbesondere wurde ein optisches Schema mit Strahlteilern zum Erhalten von Interferenz sowie ein Detektions- und Quantenlöschschema unter Verwendung von zwei Abwärtswandlern in Betracht gezogen. In den Kommentaren gab es viele Diskussionen über die Funktionsfähigkeit eines solchen Schemas sowie Kritik seitens des Benutzers, dass die Verwendung von Abwärtswandlern zu Wechselwirkungen mit dem Originalteilchen, Phasenverschiebung des Interferenzmusters und anderen unangenehmen Folgen führt. Ich schließe diese Möglichkeit nicht aus, daher habe ich mich nach eingehender Prüfung entschlossen, die Verwendung von Abwärtswandlern auszuschließen und eine Schaltung mit zirkularen und linearen Polarisatoren aufzubauen. Mit Blick auf die Zukunft kann ich sagen, dass diese Lösung ihre eigenen Schwierigkeiten hat, aufgrund derer es unmöglich ist, sich ein Bild von Störungen zu machen. Um diese Schwierigkeiten zu lösen, werden wir den eleganten Ansatz verwenden, der sich aus den Konsequenzen der Quantenmechanik selbst ergibt. Ich bin allen zutiefst dankbar, die an der Diskussion des letzten Artikels teilgenommen haben. Ihre Argumente und Kritik haben mir geholfen, die damit verbundenen Schwierigkeiten besser zu verstehen, mehr Informationen zu suchen und neue Lösungen zu finden.

Betrachten Sie zunächst einen echten Versuchsaufbau . Der Laserstrahl trifft auf ein nichtlineares optisches Gerät: einen Barium-Beta-Borat-Kristall (BBO), aufgrund dessen ein Photon in zwei verschränkte niederfrequente Photonen umgewandelt wird. Ein Prozess, der als spontane parametrische Streuung bekannt ist. Das resultierende Photonenpaar folgt verschiedenen Pfaden, von denen einer direkt zum Detektor 1 führt und der zweite durch einen Doppelspalt verläuft und in den Detektor 2 eintritt. Beide Detektoren sind mit der Koinzidenzschaltung verbunden, um sicherzustellen, dass nur verschränkte Photonenpaare berücksichtigt werden. Ein Schrittmotor bewegt den zweiten Detektor und scannt den Zielbereich, wodurch eine Intensitätskarte erstellt wird, die ein bekanntes Interferenzmuster bildet.


Bei einem Photon, das durch einen Doppelspalt läuft, werden vor jedem Spalt Zirkularpolarisatoren angeordnet, die beim Durchgang durch einen Spalt eine Polarisation des Lichts im Uhrzeigersinn und beim Durchgang durch einen anderen Spalt gegen den Uhrzeigersinn bewirken. Photonen, die im Uhrzeigersinn durch den Polarisator laufen, können den gegen den Uhrzeigersinn gerichteten Polarisator nicht passieren. Und die Photonen, die den Polarisator jeweils gegen den Uhrzeigersinn passieren, können den im Uhrzeigersinn gerichteten Polarisator nicht passieren. Zirkularpolarisatoren „markieren“ Photonen und zerstören das Interferenzmuster am zweiten Detektor ( Fresnel-Arago-Gesetze ).

Als nächstes wird ein linearer Polarisator in den Weg des ersten Photons eingeführt, der es ermöglicht, eine diagonale Polarisation von Photonen zu erhalten. Die Verschränkung sorgt auch für eine zusätzliche diagonale Polarisation in ihrem Partner, die durch eine doppelte Lücke verläuft. Dies verändert die Wirkung von Zirkularpolarisatoren - jetzt kann jedes Photon Zirkularpolarisatoren im und gegen den Uhrzeigersinn passieren. Somit ist es nicht mehr möglich zu bestimmen, welchen Weg die Photonen zurückgelegt haben, und Interferenzstreifen werden wiederhergestellt.

Betrachten Sie dies im folgenden Beispiel genauer. Stellen Sie sich vor, Alice verwendet eine lineare oder zirkulare Polarisation für den ersten Detektor und beeinflusst sofort Bobs Ergebnisse für den zweiten Detektor. Angenommen, ein BBO-Kristall erzeugt den folgenden Zustand:


Wenn Alice einen Zirkularpolarisator vor einen Detektor stellt, der im Uhrzeigersinn polarisierte Photonen filtert, hat das entsprechende Bob-Photon jedes Mal, wenn Alice ein Photon misst, notwendigerweise eine Polarisation im Uhrzeigersinn:


Da Bob gegenüber jedem Spalt gegenüberliegende Polarisationsfilter platziert hat, wissen wir, dass diese Photonen nur den ersten Spalt passieren können (sagen wir). Aus dieser Lücke fallen sie entsprechend der Wellenfunktion auf den Bildschirm:


Dabei ist a der Abstand zwischen den Schlitzen, d der Abstand zwischen den Schlitzen und dem Bildschirm und x der Abstand zur Mitte des Bildschirms. Die Lichtintensität auf dem Bildschirm (die Anzahl der Photonen) ist mit anderen Worten proportional zum Quadrat der Amplitude dieser Welle


In ähnlicher Weise wird, wenn Alice ein Photon mit einer Polarisation gegen den Uhrzeigersinn misst, das entsprechende Bob-Photon gegen den Uhrzeigersinn polarisiert, das nur durch den zweiten Spalt hindurchtreten und mit einer Wellenfunktion auf den Bildschirm gelangen kann


Beachten Sie, dass der einzige Unterschied das a / 2-Vorzeichen ist, da das Photon von einem anderen Spalt emittiert wurde. Auf dem Bildschirm sehen wir auch einen Punkt - aber dies ist ein weiterer Punkt, der um eine Strecke a verschoben ist. Es gibt einen wichtigen Punkt: Wenn Bob nie herausfindet, welche Polarisation Alice angewendet hat, sieht Bob tatsächlich die Summe zweier Intensitäten auf seinem Bildschirm:


da beide in gleichen Mengen durch Kristall hergestellt werden. Bob kann nur zwei Peaks in seinen Daten unterscheiden. Erst nachdem er die Ergebnisse von Alices Messung erhalten hat, kann er sehen, dass für den Satz von Photonen, bei dem Alice die Polarisation im Uhrzeigersinn gemessen hat, die Teilmenge von Bobs Photonen gemäß verteilt wurde und für einen Satz von Photonen, bei dem Alice die Polarisation gegen den Uhrzeigersinn misst, wird eine Teilmenge von Bobs Photonen entsprechend verteilt

(zwei Peaks und ihre Summe, wenn Alice die Polarisation von Photonen mit einem Zirkularpolarisator misst)

Betrachten Sie nun die Situation, in der Alice einen linearen Polarisator anstelle eines kreisförmigen verwendet. Als erstes müssen Sie die Wellenfunktion des Systems in Form linearer Polarisationszustände aufschreiben:


Wenn Alice einen horizontalen Polarisator verwendet, befindet sich Bobs Photonenwellenfunktion im Uhrzeigersinn und gegen den Uhrzeigersinn in einem Zustand der Polarisationsüberlagerung. Dies bedeutet, dass das Photon tatsächlich beide Schlitze passieren kann! Wenn wir auf den Bildschirm treffen, erhalten wir die Amplitude der Welle

und seine Intensität

wo repräsentiert die Phasendifferenz zwischen zwei Wellenfunktionen an der x-Position auf dem Bildschirm. Jetzt hat der Bildschirm wirklich ein Interferenzbild! Wenn Alice einen vertikalen Polarisator verwendet, ist die Amplitude von Bobs Photonenwellen ähnlich

und Intensität

Wiederum erscheint ein Interferenzmuster auf dem Bildschirm, das sich jedoch aufgrund der Phasendifferenz der Photonen, die die horizontalen und vertikalen Polarisatoren kreuzen, geringfügig gegenüber dem vorherigen Muster geändert hat.

Kann Alice also eine Nachricht an Bob senden und ihre Nachricht mit linearen und zirkularen Polarisatoren codieren? Leider gibt es keine. Da Bob nicht informiert wurde, welche Polarisation Alice verwendet hatte, sieht er nur die Summe zweier Interferenzen. Daher das Ergebnis


ist wieder ein Fleck.


(zwei Interferenzmuster und ihre Summe, wenn Alice die Polarisation von Photonen mit einem linearen Polarisator misst)

Die Korrelationen variieren je nachdem, welches Experiment Alice durchführt. Trotz der Tatsache, dass das Gesamtbild das gleiche ist, ergeben die beiden Teilmengen radikal unterschiedliche Korrelationen: Wenn Alice eine lineare Polarisation verwendet, wird das vollständige Bild auf dem Bildschirm aus zwei Interferenzmustern gebildet, und wenn Alice eine zirkulare Polarisation verwendet, ist das Bild die Summe zweier Spitzen.

Um Interferenzen zu erkennen, müssen Sie dieses Experiment wie folgt modifizieren: Anstelle von zwei Steckplätzen mit Zirkularpolarisatoren muss ein Mach-Zehnder-Interferometer installiert werden. Betrachten wir das Funktionsprinzip dieses Interferometers genauer und versuchen herauszufinden, was sich bei seiner Verwendung ändert.

MACH ZENDER INTERFEROMETER
Am Eingang des Interferometers befindet sich ein durchscheinender Spiegel, der den Lichtfluss in zwei Strahlen aufteilt. Sie spiegeln zwei undurchsichtige Spiegel wider und werden in einem zweiten durchscheinenden Spiegel zusammengeführt. Wenn das Photon ein klassisches Teilchen wäre, könnte es mit einer Wahrscheinlichkeit von 50% den ersten durchscheinenden Spiegel passieren, und mit einer Wahrscheinlichkeit von 50% wird es von ihm reflektiert.
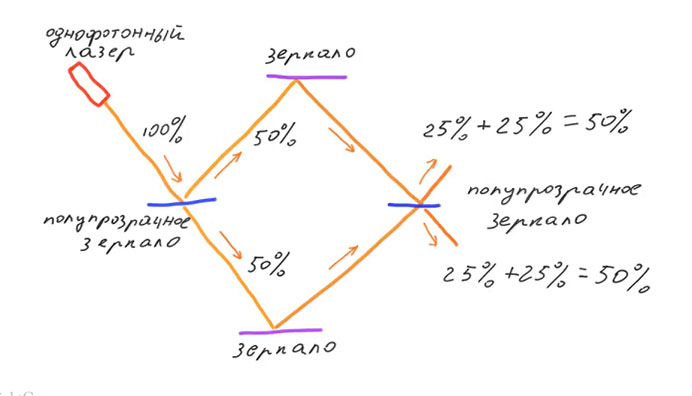
Angenommen, ein Photon passiert den ersten durchscheinenden Spiegel und bewegt sich entlang des unteren Zweigs. Auf dem zweiten durchscheinenden Spiegel kann er auch mit einer Wahrscheinlichkeit von 50% passieren oder reflektiert werden. Das heißt, der Beitrag des unteren Zweigs ist wie folgt: 25% der anfänglichen Anzahl von Photonen bewegen sich nach dem zweiten durchscheinenden Spiegel nach oben und 25% nach unten. Wenn das Photon am ersten durchscheinenden Spiegel reflektiert wird und entlang des oberen Zweigs verläuft, kann es am zweiten durchscheinenden Spiegel entweder passieren oder reflektiert werden. Der Beitrag des oberen Zweigs wird ebenfalls 25% nach oben und unten betragen. Die Gesamtwahrscheinlichkeit ist die Summe der Beiträge von zwei Zweigen und beträgt 50%, dass sich das Photon nach dem Durchgang durch den zweiten durchscheinenden Spiegel nach oben und 50% nach unten bewegt.

Wenn wir ein echtes Experiment durchführen, werden wir sehen, dass sich alle Photonen, die das Gerät passieren, nach unten bewegen. Nach dem zweiten durchscheinenden Spiegel bewegt sich kein einziges Photon nach oben. Tatsache ist, dass ein Photon nach dem Passieren des ersten durchscheinenden Spiegels nicht durch klassische Wahrscheinlichkeiten, sondern durch eine Quantenüberlagerung beschrieben wird.

Wir bezeichnen durch die grundlegenden Ket-Vektoren mit Pfeilen zwei mögliche Richtungen des Photons: auf und ab. Dann wird das Photon zunächst durch den Zustandsvektor "down" beschrieben. Nach dem Durchgang durch den ersten durchscheinenden Spiegel befindet sich das Photon in einer Überlagerung der Aufwärts- und Abwärtsbasisvektoren. Diese Überlagerung ist neben dem Elektronenspin und der Polarisation des Photons eine weitere physikalische Realisierung des Qubits.
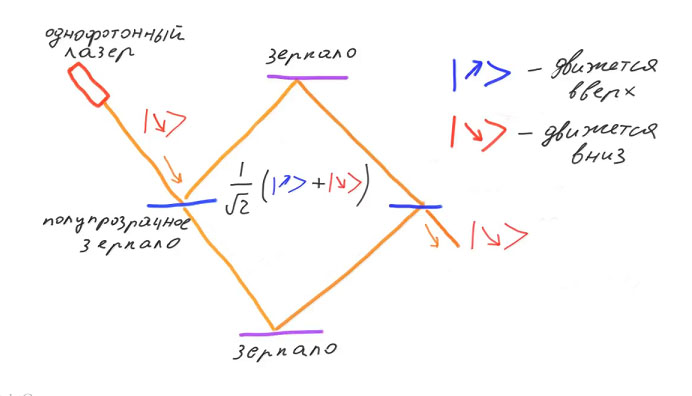
Die Quadrate des Absolutwerts der Wahrscheinlichkeitsamplituden sind die klassischen Wahrscheinlichkeiten für den Durchgang und die Reflexion eines Photons. Nach dem ersten durchscheinenden Spiegel stimmen sie mit den klassischen überein: 50%, dass sich das Photon nach oben und 50% nach unten bewegt. Nach dem Durchgang durch den zweiten durchscheinenden Spiegel ändern die Wahrscheinlichkeitsamplituden ihre Werte. Darüber hinaus kann man im Rahmen der Quantenmechanik berechnen, dass einer von ihnen Null ist und der andere. Das heißt, das Photon kehrt in den Zustand zurück, der durch den Basisvektor nach unten beschrieben wird. Mit hundertprozentiger Wahrscheinlichkeit bewegt sich das Photon nach dem Durchgang durch den zweiten durchscheinenden Spiegel nach unten.

Am Ausgang des zweiten durchscheinenden Spiegels wird nichts weiter als eine Interferenz des Photons mit sich selbst beobachtet. Wenn wir herausfinden wollen, an welchem ​​Arm des Interferometers das Photon tatsächlich vorbeigegangen ist, verschwindet die Interferenz.

EXPERIMENT
Versuchen wir, Zirkularpolarisatoren in das Mach Zehnder-Interferometer einzubauen. Installieren Sie an einem Arm des Interferometers einen Zirkularpolarisator im Uhrzeigersinn. Stellen Sie den Zirkularpolarisator auf der anderen Schulter gegen den Uhrzeigersinn ein. Darüber hinaus ist am Oberarm direkt hinter dem durchscheinenden Spiegel ein Zirkularpolarisator installiert. Am Unterarm ist nach dem reflektierenden Spiegel ein Zirkularpolarisator installiert. Tatsache ist, dass ein zirkular polarisiertes Photon, das von einem Spiegel reflektiert wird, die Polarisationsrichtung umkehrt. Daher wird für Photonen, die nicht von einem durchscheinenden Spiegel reflektiert werden, nach der Reflexion vom Spiegel eine zirkulare Polarisation hergestellt.
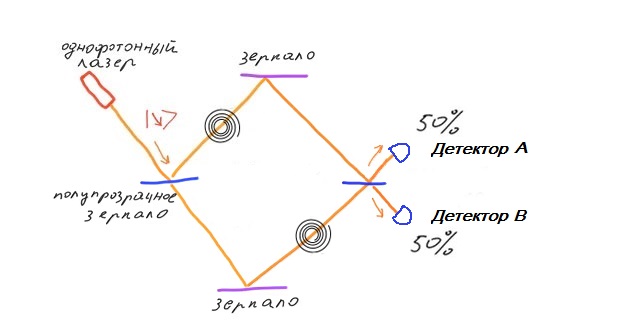
Das Vorhandensein von Polarisatoren im Interferometer gibt das Potenzial, den Weg zu bestimmen, auf dem das Photon passierte. Daher passiert das Photon entweder entlang der oberen Schulter oder entlang der unteren Schulter und passiert niemals beide Schultern gleichzeitig. Dementsprechend beobachten wir keine Störungen am Ausgang. Das Fehlen von Interferenzen führt dazu, dass am Ausgang 50% der Photonen nach oben und 50% der Photonen nach unten gerichtet sind.

Die Situation wird sich ändern, wenn wir quantenverschränkte Teilchen verwenden. Angenommen, ein Laserstrahl trifft auf ein nichtlineares optisches Gerät: einen Barium-Beta-Borat-Kristall (BBO), aufgrund dessen ein Photon in zwei verschränkte Photonen einer niedrigeren Frequenz umgewandelt wird. Das resultierende Photonenpaar folgt verschiedenen Pfaden, von denen einer durch den Polarisator geht und direkt zum Detektor 1 geht , und der zweite durch ein Interferometer mit Zirkularpolarisatoren geht und zum Detektor 2 oder 3 geht .
Wenn wir einen Zirkularpolarisator in den Weg des ersten Photons legen, sehen wir auch keine Interferenz. Dementsprechend erhalten wir am Ausgang 50% der nach oben gerichteten Photonen und 50% der nach unten gerichteten Photonen.
Wenn jedoch ein diagonal angeordneter linearer Polarisator auf dem Weg des ersten Photons platziert wird, sorgt der verschränkte Zustand für eine zusätzliche diagonale Polarisation in seinem Partner. Das Vorhandensein einer zusätzlichen linearen Polarisation ermöglicht es Photonen, durch beide Arme zu gelangen und sich selbst zu stören. In diesem Fall weist die Interferenz eine Phasendifferenz auf (Photonen, deren Partner den linearen Polarisator passiert haben und deren Partner nicht passierten, erzeugen eine Interferenz auf dem Bildschirm, die zueinander versetzt ist). Trotzdem kehrt das Photon am Ausgang des zweiten durchscheinenden Spiegels in den durch den Basisvektor nach unten beschriebenen Zustand zurück. Daher bewegen sich nach dem Durchgang durch den zweiten durchscheinenden Spiegel alle Photonen nach unten.

Ein solches Implementierungsschema ist insofern praktisch, als es nicht erforderlich ist, ein Koinzidenzmuster von verschränkten Teilchen zu erstellen, Photonen einzeln zu emittieren und die Position jedes Photons auf dem Bildschirm zu analysieren. Durch Installieren oder Entfernen eines linearen Polarisators im Pfad verwickelter Partikel können Sie die Verteilung ihrer Partner zwischen den Detektoren 2 und 3 sofort beeinflussen. Es reicht aus, die Lichtflussintensität in beiden Detektoren zu vergleichen und das übertragene Informationsbit zu bestimmen. Natürlich werden am Ausgang des BBO-Kristalls nicht alle Photonen verwickelt. Die Anzahl der verwickelten Paare beträgt mehrere zehn Prozent der Gesamtzahl. Aber auch eine kleine Änderung der Lichtintensität kann von Detektoren erfasst werden, die die übertragenen Informationen entschlüsseln. Das zweite große Plus ist, dass verschränkte Paare sich nicht überlagern. Dies ermöglicht es ihnen, mit der Umgebung zu interagieren und die übertragenen Informationen im Gegensatz zur Quantenteleportation nicht zu zerstören, wenn die Interaktion mit Luft oder einem optischen Kabel die Wellenfunktion des Photons zerstört.

VERWANDTE PROBLEME
Durch die Verwendung solcher Schemata wird eine minimale Verzögerung bei der Übertragung von Informationen über große Entfernungen erreicht. Die Geschwindigkeit der Informationsübertragung kann die Lichtgeschwindigkeit im Vakuum erheblich überschreiten. Einige argumentieren, dass STO / GTR die Übertragung von Informationen mit einer Geschwindigkeit über der Lichtgeschwindigkeit verbietet. Die Idee der Endlichkeit der Lichtgeschwindigkeit wurde von Poincare vorgeschlagen und aus Maxwells Formeln abgeleitet. In diesem Fall war es zunächst ein elektromagnetisches Feld und wurde dann mit der leichten Hand von Albert Germanovich auf alle massiven und masselosen materiellen Objekte ausgedehnt. Es ist wichtig zu betonen, dass nicht über Informationen gesprochen wurde. Wenn Sie ein Buch über STO / GRT öffnen, sind Informationen im mathematischen Formalismus nicht vorhanden. Wenn sie behaupten, dass STO / GTR die Übertragung von Informationen über die Lichtgeschwindigkeit verbietet, wird implizit angenommen, dass es keinen anderen Weg gibt, als Informationen auf einem Photonen- / Elektronenstrahl usw. zu "pflanzen". existiert nicht.

PRINZIP DER URSACHE
Eines der Hauptprobleme der sofortigen Informationsübertragung ist die Verletzung des Kausalitätsprinzips. Sie können jedoch sehen, dass die moderne Physik keine Einhaltung der Kausalität auf Quantenebene erfordert und daher nicht zu den Postulaten der Physik gehört. Es gibt Quantenexperimente, bei denen der Zeitpfeil durchaus umgekehrt werden kann. Der Mensch kann sich jedoch noch nicht weigern, der Kausalität nachzukommen, da dies unserer Logik widerspricht.

Nach Einsteins Relativitätstheorie ermöglicht die sofortige Übertragung von Informationen den Empfang von Informationen, bevor sie gesendet werden. Wenn wir uns beispielsweise dazu entschließen, Informationen an uns selbst zu senden, können wir ein Experiment so durchführen, dass Informationen abgerufen werden, bevor wir sie senden. Angenommen, wir übertragen Informationen mithilfe eines komplizierten Paares. Dann passiert ein Photon das Interferometer und gelangt zum Detektor, und das zweite Photon geht zum Beispiel zum Mond, wo es vom Spiegel reflektiert wird und zu uns zurückkehrt.
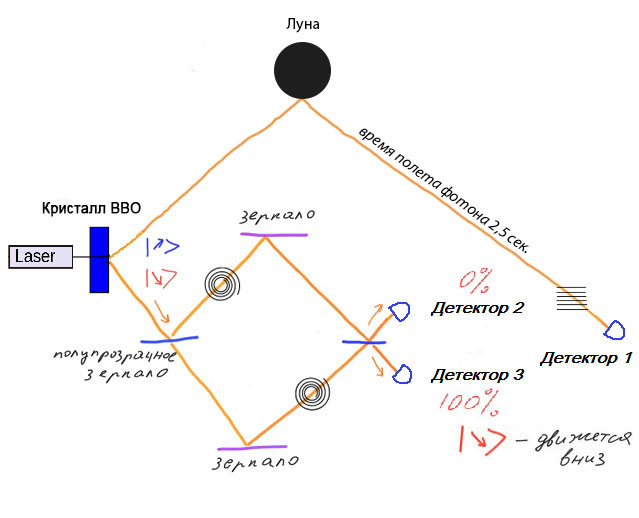
Durch Installieren oder Entfernen eines linearen Polarisators im Pfad des zweiten Photons können wir das Ergebnis am Ausgang des Interferometers beeinflussen. Wenn wir also die Detektoren am Ausgang des Interferometers beobachten, wissen wir im Voraus, welche Informationen wir in 2,5 Sekunden senden möchten (die Flugzeit der Photonen zum Mond und zurück). Dies kann zum "Paradoxon des getöteten Großvaters" führen, als wir eine Bedeutung sahen und beschlossen, das Gegenteil zu senden.

Dieses Problem kann durch Hugh Everetts Theorie alternativer Realitäten gelöst werden, die heute viele Befürworter hat. Nach Everetts Theorie gibt es unzählige alternative Realitäten. Bei jeder Wahlmöglichkeit ist unsere Realität in mehrere alternative Realitäten unterteilt, in denen alle möglichen Wahlmöglichkeiten verwirklicht werden. Realitäten können sich überschneiden und auseinander gehen und viele Optionen für die Vergangenheit und Zukunft bilden.

Nach dieser Theorie ist die Interferenz auf zwei Schlitzen der Schnittpunkt zweier ähnlicher Realitäten ohne Kollaps der Wellenfunktion. In einer Realität passierte das Photon die erste Lücke, in einer anderen Realität passierte das Photon die zweite Lücke. Am Schnittpunkt zweier Realitäten stellt sich heraus, dass das Photon beide Schlitze passiert hat. Wir können nicht genau herausfinden, durch welche Lücke das Photon gegangen ist, da die Vergangenheit des Photons für uns ungewiss ist. Gleiches gilt für die Zukunft. Nach der Emission eines Photons können wir nicht wissen, wo es sich befindet. Ein Photon kann überall lokalisiert werden, und in jeder Version der Zukunft wird eine der Wahrscheinlichkeiten realisiert, bei der die Flugbahn des Photons genau definiert ist.

Wenn Hugh Everetts Theorie richtig ist, führt unsere Entscheidung, anstelle des Gesehenen den entgegengesetzten Wert zu senden, nicht zum "Paradox eines toten Großvaters". In diesem Fall wird auf dem Bildschirm nur der Durchschnittswert der beiden möglichen Optionen angezeigt, anhand derer wir nicht mehr bestimmen können, welche Informationen wir uns in Zukunft selbst senden möchten. Wir können jede Option senden und dies wird zu keinen Problemen führen.

Echte Experimente werden es uns vielleicht ermöglichen, eine experimentelle Bestätigung dieser Theorie zu erhalten. Eine indirekte Bestätigung der Theorie liegt zwar bereits vor. Zum Beispiel ist es möglich, eine Fotografie von mikroskopischen Objekten zu erhalten, ohne das zu untersuchende Objekt zu stören (d. H. Kein einzelnes Photon auf das Objekt zu richten). Dieses Phänomen wird aktiv untersucht, um neue Mikroskoptypen zu bauen.

ENTROPY
Wie wir wissen, ist Entropie ein Maß für Störung. Es wird angenommen, dass der Lauf der Zeit zu einer Zunahme der Entropie führt. Dies bedeutet, dass die Vergangenheit weniger Entropie haben sollte als die Zukunft. Und wenn wir versuchen, in die Vergangenheit zurückzukehren, führt dies zu einem Problem der erhöhten Entropie. Tatsächlich ist Entropie in keiner Weise mit der Übertragung von Informationen verbunden, da wir keine materiellen Körper in die Vergangenheit senden. Daher kann das Problem der erhöhten Entropie thermodynamischer Systeme nicht auf Photonen angewendet werden.

ANALYSE DER ZUKUNFT
Die Theorie der Multi-World-Interpretation bedeutet nicht, dass es keine Möglichkeit gibt, verlässliche Informationen aus der Zukunft zu erhalten. Die Verwendung des obigen Schemas in deterministischen Systemen ermöglicht es, eine zuverlässige Prognose mit hoher Wahrscheinlichkeit zu erhalten. Wenn wir beispielsweise herausfinden möchten, ob der Mond morgen verschwinden wird, ist diese Wahrscheinlichkeit in vielen alternativen Szenarien (die von unserer aktuellen Realität abweichen) minimal. Dementsprechend zeigen die Ergebnisse des Experiments überwiegend eine Antwort. Sie können auch eine Wettervorhersage mit einem hohen Maß an Zuverlässigkeit erhalten, indem Sie eine Vielzahl von Berechnungen in Supercomputern umgehen. Die Anwendungsmöglichkeiten im Bereich der Prognose sind sehr groß. Eine der wichtigen Aufgaben für die Analyse kann die Vorhersage kritischer Entscheidungen sein (z. B. der Ausbruch von Feindseligkeiten undmöglicherweise ein Atomschlag auf den Feind) und eine Analyse ihrer Folgen.

Es ist anzumerken, dass die tatsächliche Verwendung im Bereich der Prognose der Zukunft noch weit entfernt ist. Um eine Verzögerung von einem Tag zu erhalten, müssen Sie den dielektrischen Spiegel an die Grenze des Sonnensystems bringen und einen sehr hochwertigen Laser mit einem minimalen Divergenzwinkel herstellen. Wenn Sie den Strahl mehrfach reflektieren, müssen Sie perfekt reflektierende dielektrische Spiegel erstellen. Beispielsweise muss ein Laserstrahl zwischen Erde und Mond 70.000 Mal am Tag reflektiert werden. Vielleicht wäre die Lösung, die Lichtgeschwindigkeit mit einem unterkühlten Medium, dem Bose-Einstein-Kondensat, zu verlangsamen. Soweit ich weiß, ist es den Physikern des Rowland Institute of Scientific Research gelungen, die Lichtgeschwindigkeit auf 17 Meter pro Sekunde zu verlangsamenund einige Jahre später gelang es einer Gruppe von Wissenschaftlern der Harvard University sogar, das Licht für 10 bis 20 ms vollständig zu stoppen .

PS Leider funktionierte dieses Schema nicht, da eine sorgfältige Überprüfung der Berechnungen ergab, dass die Phasenverschiebung bei der Verwendung von quantenverschränkten Partikeln nicht korrekt berücksichtigt wurde.

Quellen:
Quantenradierer
Interferenz Qubit mit sich selbst
realistisch mnogomirie?