Erstellen von Umlaufbahnen von Himmelskörpern mit Python

Referenzsysteme zur Bestimmung der Umlaufbahn

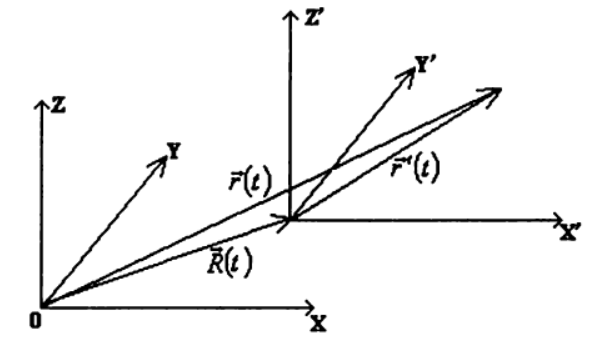
Um die Trajektorien relativer Bewegungen in der klassischen Mechanik zu ermitteln, wird die Annahme der absoluten Zeit in allen Referenzrahmen (sowohl Trägheits- als auch Nicht-Trägheitsrahmen) verwendet.

Unter dieser Annahme betrachten wir die Bewegung desselben Punktes in zwei verschiedenen Referenzrahmen $$$K$ und $$$K ^ {'}$ von denen sich die zweite relativ zur ersten mit einer beliebigen Geschwindigkeit bewegt $$$\ vec {V (t)} = \ dot {\ vec {R (t)}}$ wo $$$\ vec {R (t)}$ Radiusvektor, der die Position des Ursprungs des Koordinatensystems beschreibt $$$K ^ {'}$ relativ zum Bezugsrahmen $$$K$ )

Wir werden die Bewegung eines Punktes im System beschreiben $$$K ^ {'}$ Radiusvektor $$$\ vec {r ^ {'}} (t)$ vom Ursprung des Systems gerichtet $$$K ^ {'}$ auf die aktuelle Position des Punktes. Dann die Bewegung des betrachteten Punktes relativ zum Referenzrahmen $$$K$ beschrieben durch einen Radiusvektor $$$\ vec {r (t)}$ ::

$$$\ vec {r} (t) = \ vec {r ^ {'}} (t) + \ vec {R} (t)$ , (1)

und relative Geschwindigkeit $$$\ vec {v (t)}$

$$$\ vec {v} (t) = \ dot {\ vec {r ^ {'}}} (t) + \ dot {\ vec {R}} (t)$ , (2)

wo $$$\ dot {\ vec {r ^ {'}}} (t)$ - Geschwindigkeit des Punktes relativ zum System $$$K ^ {'}$ ;; $$$\ dot {\ vec {R}} (t)$ -frame Geschwindigkeit $$$K ^ {'}$ relativ zum Bezugsrahmen $$$K$ .



So finden Sie das Bewegungsgesetz eines Punktes in einem beliebigen Referenzrahmen $$$K$ notwendig:

1) setze das Bewegungsgesetz des Punktes - $$$\ vec {r ^ {'}} (t)$ relativ zum Bezugsrahmen $$$K ^ {'}$ ;;
2) das Bewegungsgesetz festlegen - $$$\ vec {R} (t)$ Referenzsysteme $$$K ^ {'}$ relativ zum Bezugsrahmen $$$K$
3) das Bewegungsgesetz des Punktes bestimmen - $$$\ vec {r} (t) = \ vec {r ^ {'}} (t) + \ vec {R} (t)$ relativ zum Bezugsrahmen $$$K$ .

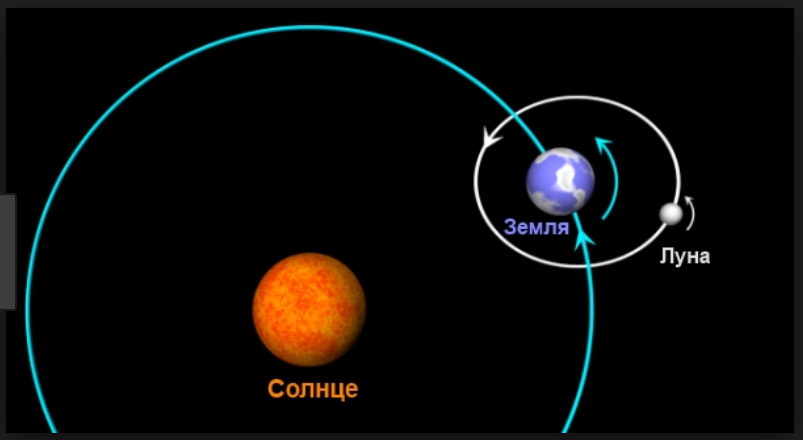
Konstruktion der Mondbahn im heliozentrischen Referenzrahmen

Im heliozentrischen Bezugssystem (System $$$K$ ) Die Erde bewegt sich in einem Radiuskreis
$$$R_ {1} = 1.496 \ cdot 10 ^ {8}$ km (Umlaufzeit $$$T_ {1} = 3.156 \ cdot 10 ^ {7}$ s.). Der Mond bewegt sich wiederum um die Erde (System K ') um einen Radiuskreis $$$R_ {2} = 3.844 \ cdot 10 ^ {5}$ km (Umlaufzeit $$$T_ {2} = 2.36 \ cdot 10 ^ {6}$ s Wie bekannt [1,2], wenn sich ein Materialpunkt entlang eines Radiuskreises bewegt $$$R$ mit konstanter Winkelgeschwindigkeit $$$\ omega$ Die Koordinaten des Radiusvektors, die vom Ursprung zur aktuellen Position des Punktes gezogen werden, ändern sich gemäß dem Gesetz:

$$

$$\ vec {R (t)} = \ binom {R \ cdot cos (\ omega \ cdot t + \ varphi _ {0})} {R \ cdot sin (\ omega \ cdot t + \ varphi _ {0})} = \ binom {R \ cdot cos (\ frac {2 \ pi} {T}) + \ varphi _ {0})} {R \ cdot sin (\ frac {2 \ pi} {T} + \ varphi _ { 0})}, (3)$$

wo $$$\ varphi _ {0}$ - die Anfangsphase, die die Position des Partikels zum Zeitpunkt charakterisiert $$$t = 0$ , die wir in Zukunft als gleich Null annehmen werden. Ersetzen in (3) $$$R$ auf $$$R_ {1}$ und $$$R_ {2}$ und durch Einsetzen in (1) erhalten wir die Abhängigkeit des Radiusvektors des Mondes im heliozentrischen Koordinatensystem von der Zeit:

$$

$$\ vec {r (t)} = \ binom {x (t)} {y (t)} = \ binom {R_ {2} cos (\ frac {2 \ pi} {T_ {2}} t) + R_ {1} cos (\ frac {2 \ pi} {T_ {1}} t)} {R_ {2} sin (\ frac {2 \ pi} {T_ {2}} t) + R_ {1} sin (\ frac {2 \ pi} {T_ {1}} t)}, (4)$$

Ausdruck (4) legt die Umlaufbahn des Mondes fest ( $$$y = y (x (t))$ ) in parametrischer Form, wobei der Parameter die Zeit ist. Um die gewünschte Umlaufbahn mit Python zu erstellen, legen wir die Radien der Umlaufbahnen und die Rotationsperioden der Erde und des Mondes fest.

Die Erde bewegt sich in einem heliozentrischen Koordinatensystem ( $$$K$ ) sein Umlaufradius und die Umdrehungsperiode sind jeweils gleich $$$R_ {1} = 1,496 \ cdot 10 ^ {8} km, T_ {1} = 3,156 \ cdot 10 ^ {7} s$ Der Mond bewegt sich in einem Koordinatensystem um die Erde ( $$$K ^ {'}$ ) sein Umlaufradius und die Umdrehungsperiode sind jeweils gleich $$$R_ {2} = 3,844 \ cdot 10 ^ {5} km, T_ {2} = 2,36 \ cdot 10 ^ {6} s$ .

Im Hinblick auf (4) bestimmen wir die Funktionen der Abhängigkeit der Koordinaten von der Zeit:

$$

$$\ binom {(X (t) = R_ {1} \ cdot cos (\ frac {2 \ pi} {T_ {1}} \ cdot t), Y (t) = R_ {1} \ cdot sin (\ frac {2 \ pi} {T_ {1}} \ cdot t)} {x (t) = R_ {2} \ cdot cos (\ frac {2 \ pi} {T_ {2}} \ cdot t), y (t) = R_ {2} \ cdot sin (\ frac {2 \ pi} {T_ {2}} \ cdot t)}, (5)$$

Mit (5) erhalten wir ein Koordinatenpaar für die Umlaufbahn des Mondes:

$$

$$\ binom {X_ {g} (t) = X (t) + x (t)} {Y_ {g} (t) = Y (t) + y (t)}, (6)$$

Wir legen die Anzahl der Punkte fest, an denen die Koordinaten N = 1000 und die diskrete Zeit im Intervall der Erdrotationsperiode berechnet werden $$$dt = \ frac {T_ {1}} {N}$ . Wir werden ein Programm schreiben und ein Diagramm für den positiven Koordinatenänderungsbereich erstellen:


Wir bekommen:


Abb. 1

Mit dem erstellten Zeitplan können Sie die Trainingsaufgabe erweitern und sehen, wie die Umlaufbahn des Mondes aussehen wird, wenn der Radius der Umlaufbahn des Mondes beträgt $$$R_ {2} = 3.844 \ cdot 10 ^ {7}$ . . Dem Leser, der nicht einmal über spezielle astronomische Kenntnisse verfügt, ist klar, dass der Mond in nicht-gravitativen Feldern der Erde keine solche Umlaufbahn haben kann, und ein hypothetischer Radius wird verwendet, um die Bedingungen für das Auftreten von Schleifen zu untersuchen . Wir werden die entsprechenden Änderungen am Programm vornehmen:


Wir bekommen:


Abb.2

Vergleich der Umlaufbahnen des Mondes in Abb. 1 und 2 finden wir ihre signifikanten Unterschiede. Um die Gründe für diese Unterschiede zu erklären, müssen die linearen Geschwindigkeiten des Mondes im ersten und zweiten Fall und die lineare Geschwindigkeit der Erde verglichen werden.

Da sich die Richtung der linearen Geschwindigkeit der Erde relativ zur Sonne sowie die Richtung der linearen Geschwindigkeit des Mondes relativ zur Erde zeitlich ändert und die Geschwindigkeit in ihrer Größe konstant bleibt.

Als quantitatives Merkmal des Verhältnisses der linearen Geschwindigkeiten von Mond und Erde im heliozentrischen Koordinatensystem sollte man die Differenz zwischen dem linearen Geschwindigkeitsmodul der Erde und der Projektion der linearen Geschwindigkeit des Mondes auf die Richtung des linearen Geschwindigkeitsvektors der Erde wählen:

$$

$$v_ {o} (t) = \ left | \ vec {V} (t) \ right | - \ frac {(\ vec {V} (t) \ cdot \ vec {v} (t))} {\ left | \ vec {V} (t) \ right |}, (7)$$

Wir definieren die Funktionen, die die Gesetze der Änderung der Komponenten der Geschwindigkeit der Erde und des Mondes beschreiben:

$$

$$\ begin {matrix} V_ {x} (t) = \ frac {d} {dt} X (t), V_ {y} (t) = \ frac {d} {dt} Y (t) & \\ vx (t) = \ frac {d} {dt} x (t), vy (t) = \ frac {d} {dt} y (t) \ end {matrix}, (8)$$

Um die resultierende Geschwindigkeit unter Berücksichtigung der Projektion zu bestimmen, verwenden wir die Beziehung:

$$$D (t) = \ sqrt {V_ {x} (t) ^ {2} + V_ {y} (t) ^ {2}} - \ sqrt {vx (t) ^ {2} + vy (t) ^ {2}} \ cdot \ frac {V_ {x} (t) \ cdot vx (t) + V_ {y} (t) \ cdot vy (t)} {\ sqrt {V_ {x} (t) ^ {2} + V_ {y} (t) ^ {2}} \ cdot \ sqrt {vx (t) ^ {2} + vy (t) ^ {2}}}, (9)$

Wir werden ein Programm schreiben, das (5), (8), (9) und den Radius der Mondbahn berücksichtigt $$$R_ {2} = 3.844 \ cdot 10 ^ {5}$ km .:


Wir bekommen:


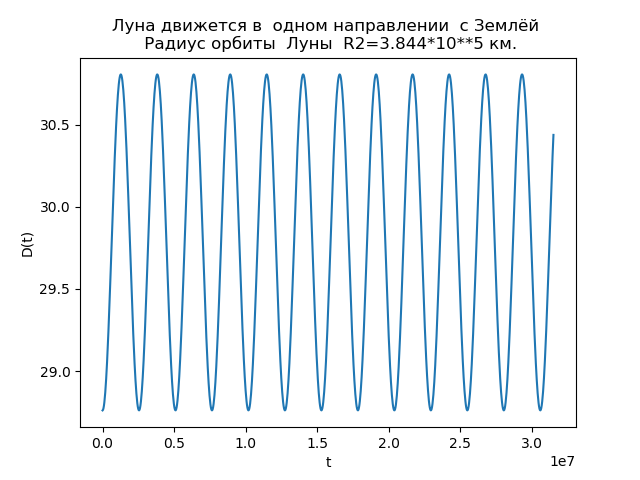Abb. 3.

Wir werden ein Programm schreiben, das (5), (8), (9) und den Radius der Mondbahn R2 = 3,844 * 10 ** 7 km berücksichtigt:


Wir bekommen:


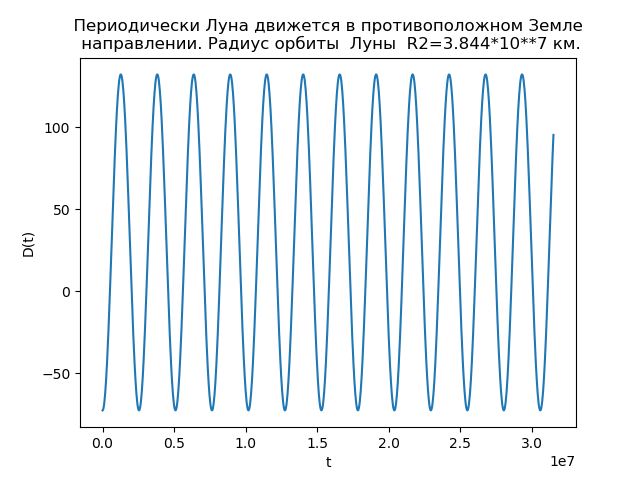Abb. 4.

Die Analyse der Abhängigkeiten ermöglicht es uns, den Grund für die Unterschiede in den Umlaufbahnen zu erklären. Die Funktion D (t) für $$$R_ {2} = 3.844 \ cdot 10 ^ {5}$ km ist immer positiv, dh der Mond bewegt sich immer in Richtung der Erdbewegung und es bilden sich keine Schleifen. Bei $$$R_ {2} = 3.844 \ cdot 10 ^ {7}$ km Wert $$$D (t)$ nimmt negative Werte an, und es gibt Zeiten, in denen sich der Mond in die der Bewegungsrichtung der Erde entgegengesetzte Richtung bewegt, und daher hat die Umlaufbahn Schleifen. Dies war die Bedeutung der Verwendung der nicht existierenden Umlaufbahn des Mondes in den Berechnungen.

Konstruktion der Marsbahn im Bezugsrahmen zur Erde

.


Im heliozentrischen Bezugssystem (System K) bewegt sich die Erde in einem Radiuskreis $$$R_ {1} = 1.496 \ cdot 10 ^ {8}$ km, Umlaufzeit $$$T_ {1} = $ 365,2$ Tag bewegt sich der Mars entlang einer Ellipse, deren Hauptachse $$$am = 2.28 \ cdot 10 ^ {8}$ km, die Zeit der Revolution des Mars $$$T_ {m} = $ 689,9$ Tage., die Exzentrizität der Umlaufbahn $$$e = $ 0,09$ [3]. Die Bewegung der Erde wird durch den durch Ausdruck (3) definierten Radiusvektor R (t) beschrieben. Aufgrund der Tatsache, dass die Umlaufbahn des Mars eine Ellipse ist, Abhängigkeiten $$$x = x (t), y = y (t)$ ab Zeit werden parametrisch eingestellt [4]:

$$$x (\ varepsilon) = a_ {m} \ cdot (cos (\ varepsilon) -e)$ , (10)

$$$y (\ varepsilon) = a_ {m} \ cdot \ sqrt {1-e ^ {2}} \ cdot sin (\ varepsilon)$ , (11)

$$$t (\ varepsilon) = \ frac {T_ {m}} {2 \ pi} \ cdot (\ varepsilon-e \ cdot sin (\ varepsilon))$ , (12)

Eine vollständige Ellipsenumdrehung entspricht einer Änderung des Parameters <img $$$\ varepsilon$ von 0 bis $$$2 \ pi$ . Um die Umlaufbahn des Mars aufzubauen, müssen die Koordinaten der Radiusvektoren zu den gleichen Zeitpunkten berechnet werden, die die Position der Erde und des Mars im heliozentrischen Referenzrahmen beschreiben, und dann in Übereinstimmung mit der Beziehung $$$\ vec {r ^ {'}} (t) = \ vec {r} (t) - \ vec {R} (t)$ Berechnen Sie die Koordinaten des Mars im Bezugsrahmen zur Erde.

Um die Umlaufbahn des Mars in dem mit der Erde verbundenen Referenzrahmen aufzubauen, verwenden wir die zuvor angegebenen Parameter der Umlaufbahnen der Erde und des Mars, die Beziehungen (10) - (12) sowie die Beziehungen für die Koordinaten der Erde:

$$$X (t) = R_ {1} \ cdot cos (\ frac {2 \ pi} {T_ {1}} t)$ , (13)

$$$Y (t) = R_ {1} \ cdot sin (\ frac {2 \ pi} {T_ {1}} t)$ , (14)

Es sollte beachtet werden, dass die Anzahl der Umdrehungsperioden des Mars um die Sonne beträgt $$$K = 9$ , dann wird die Anzahl der Punkte, an denen die Berechnung durchgeführt werden soll, und der Abstand zwischen ihnen aus den Beziehungen bestimmt:

$$$N = 4000 \ cdot K, \ varepsilon_ {i} = \ frac {2 \ pi} {N} \ cdot i, i = 0 ... N$ (15)


Wir bekommen:


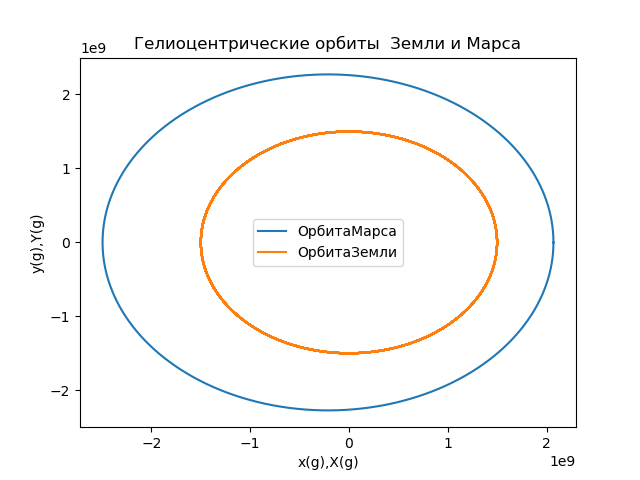Abb.5

Wir berechnen die Koordinaten des Radiusvektors, der die Position des Mars im mit der Erde verbundenen Referenzrahmen beschreibt, und konstruieren die Umlaufbahnen (Abb. 6) unter Verwendung der folgenden Beziehung:

$$$x1_ {i} = x (\ varepsilon_ {i}) - X (t (\ varepsilon_ {i})), y1_ {i} = y (\ varepsilon_ {i}) - Y (t (\ varepsilon_ {i}) ))$ (16)


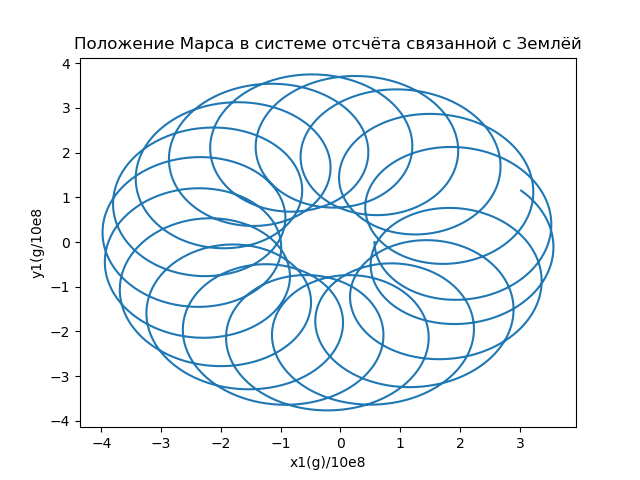Abb.6

Ein weiteres wichtiges Merkmal der Bewegung des Mars (hauptsächlich für interplanetare Raumflüge) ist der Abstand zwischen der Erde und dem Mars (t), der durch den Modul des Radiusvektors bestimmt wird, der die Position des Mars im mit der Erde verbundenen Bezugssystem beschreibt. Die Abhängigkeit der Entfernung zwischen Erde und Mars von der in Erdjahren gemessenen Zeit ist in Abb. 7 dargestellt.


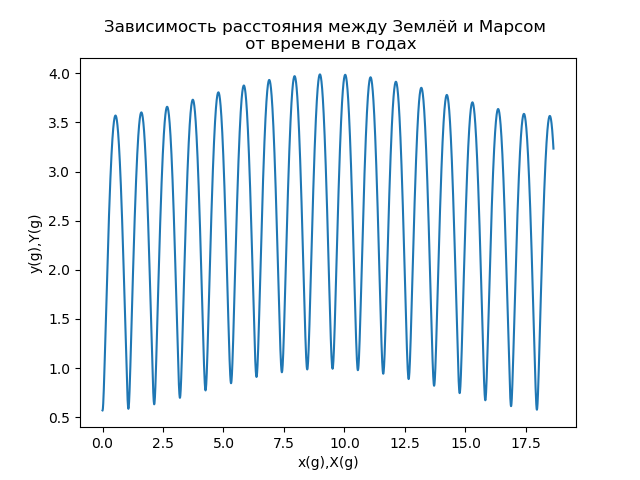Abb. 7

Eine Analyse der in Abb. 7 gezeigten Abhängigkeit zeigt, dass der Abstand zwischen Erde und Mars eine komplexe periodische Funktion der Zeit ist. Wenn wir die Terminologie der Signaltheorie [5] verwenden, können wir über die Abhängigkeit s (t) sagen, dass es sich um ein amplitudenmoduliertes Signal handelt, das normalerweise als Produkt zweier Funktionen einer Hochfrequenz- (Träger-) und Niederfrequenzfunktion dargestellt wird, die die Amplitudenmodulation (Hüllkurve) definiert. ::

$$$u (t) = (\ bar {u} + a \ cdot sin (\ omega_ {1} t)) \ cdot (1+ \ Delta a \ cdot sin (\ omega_ {2} t))$ (17)

wo $$$\ bar {u}$ - konstante Komponente der Funktion $$$u (t)$ ;; $$$a$ - Signalamplitude; $$$\ omega_ {1}$ - Trägerfrequenz; $$$\ Delta a$ - die Amplitude der Funktion, die die Tiefe der Amplitudenmodulation festlegt; $$$\ omega_ {2}$ - Frequenz der Modulationsfunktion.

Aus Fig. 7 ist ersichtlich, dass die Periode des Trägers ungefähr 2 Jahre beträgt, die Periode der Modulationsfunktion ungefähr 17 Jahre] 6].

Konstruktion der heliozentrischen Umlaufbahn des Halleyschen Kometen

Das letzte Mal, dass Halleys Komet am 9. Februar 1986 sein Perihel (den der Sonne am nächsten gelegenen Umlaufbahnpunkt) passierte. (Die Sonne selbst befindet sich am Ursprung.)

Die Koordinaten und Geschwindigkeitskomponenten von Halleys Kometen waren zu diesem Zeitpunkt gleich $$$p_ {0} = (0,325514, 0,459460, 0,166229)$ und $$$v_ {0} = (–9.096111, –6.916686, –1.305721)$ und die Entfernung wird hier in astronomischen Längeneinheiten ausgedrückt - a.u.d. oder einfach a.u. (astronomische Einheit, d. h. die Länge der Haupthalbhalbachse der Erdumlaufbahn) und Zeit in Jahren. In diesen Maßeinheiten haben die dreidimensionalen Bewegungsgleichungen des Kometen die Form:

$$

$$\ left \ {\ begin {matrix} \ frac {d ^ {2} x} {dt ^ {2}} = - \ frac {\ mu \ cdot x} {r ^ {3}} \\ \ frac { d ^ {2} y} {dt ^ {2}} = - \ frac {\ mu \ cdot y} {r ^ {3}} \\ \ frac {d ^ {2} z} {dt ^ {2} } = - \ frac {\ mu \ cdot z} {r ^ {3}} \ end {matrix} \ right., (18)$$

(18)

wo: $$$\ mu = 4 \ pi ^ {2}, r = \ sqrt {x ^ {2} + y ^ {2} + z ^ {2}}$


Wir bekommen:









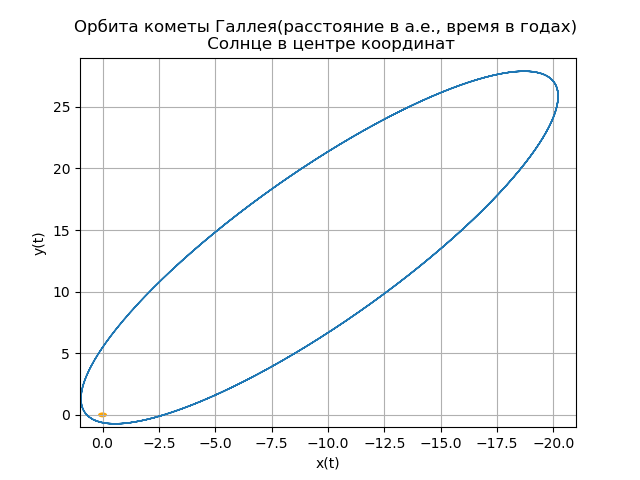
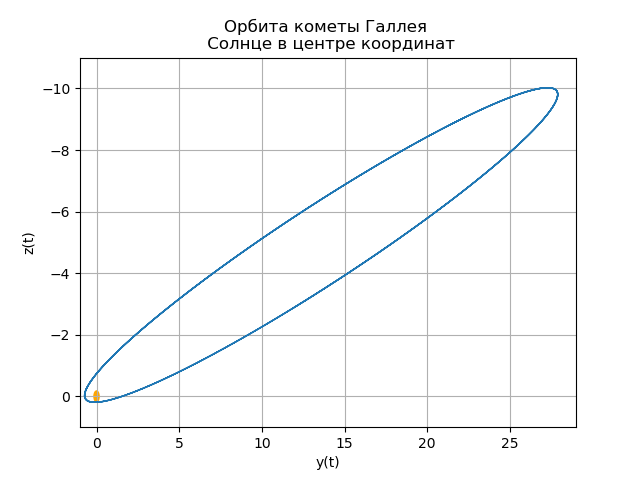
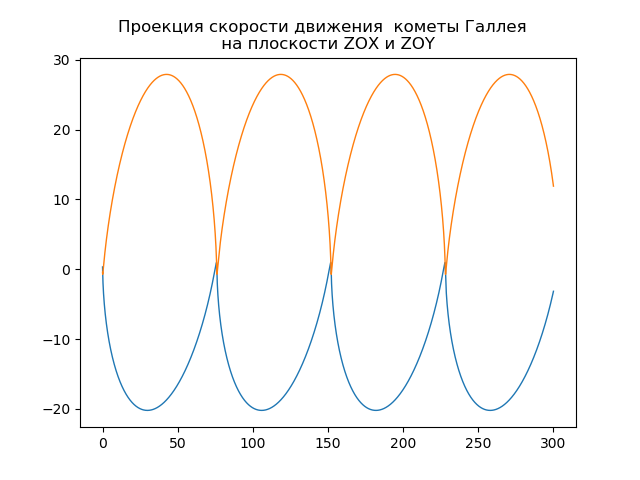Dein eigener Komet

Versuchen Sie ein Experiment. Nachts montieren Sie Ihr Teleskop auf einem Hügel unweit Ihres Hauses. Die Nacht sollte klar, wolkenlos, sternenklar sein und, wenn das Glück Sie anlächelte: um 0.30 Uhr werden Sie einen neuen Kometen bemerken.

Nach wiederholten Beobachtungen in den folgenden Nächten können Sie die Koordinaten in dieser ersten Nacht berechnen. Koordinaten im heliozentrischen Koordinatensystem: P0 = (x0, y0, z0) und der Geschwindigkeitsvektor v0 = (vx0, vy0, vz0).

Bestimmen Sie anhand dieser Daten:

• die Entfernung des Kometen von der Sonne am Perihel (dem Punkt, der der Sonne am nächsten liegt) und am Aphel (dem Punkt der Umlaufbahn, der am weitesten von der Sonne entfernt ist);
• Kometengeschwindigkeit beim Passieren des Perihels und des Aphels;
• die Zeit der Revolution des Kometen um die Sonne;
• Die nächsten beiden Daten durchläuft der Komet das Perihel.

Wenn wir die Entfernung in astronomischen Einheiten und die Zeit in Jahren messen, nimmt die Bewegungsgleichung des Kometen die Form an (18). Wählen Sie für Ihren eigenen Kometen beliebige Startkoordinaten und Geschwindigkeiten in derselben Reihenfolge wie für den Halleyschen Kometen.

Treffen Sie bei Bedarf eine beliebige Auswahl der Anfangsposition und des Geschwindigkeitsvektors, bis Sie eine plausible exzentrische Umlaufbahn erhalten, die über die Erdumlaufbahn hinausgeht (wie die meisten realen Kometen).

Referenzen:

1. Feynman R., Leighton R., Sands M. Feynman Vorlesungen in Physik. 3rd ed. T. 1.-2. M.: Mir, 1977.
2. Matveev A. N. Mechanik und Relativitätstheorie. M.: Höher. Schule., 1986.
3. Physische Enzyklopädie. T. 3. M.: Big Russian Encyclopedia, 1992.
4. Landau L.D., Lifshits E.M. Kurs in Theoretischer Physik. Die Mechanik. M.: Fu-matgiz, 1958.
5. Baskakov S. I. Funktechnische Schaltungen und Signale. M.: Höher. Schule., 1988.
6. Porshnev C.V. Computersimulation physikalischer Prozesse mit dem Mathcad- Paket.