Wie wir bei 1C: Enterprise Systeme algebraischer Gleichungen lösen

Das Arbeiten mit numerischen Matrizen im Allgemeinen und das Lösen von Systemen linearer algebraischer Gleichungen im Besonderen ist ein klassisches mathematisches und algorithmisches Problem, das häufig bei der Modellierung und Berechnung einer großen Klasse von Geschäftsprozessen (z. B. bei der Berechnung von Kosten) verwendet wird. Beim Erstellen und Betreiben von 1C: Enterprise-Konfigurationen standen viele Entwickler vor der Notwendigkeit, SLAU-Berechnungsalgorithmen manuell zu implementieren, und dann vor dem Problem, lange auf eine Lösung zu warten.

„1C: Enterprise“ 8.3.14 enthält Funktionen, mit denen sich die Zeit zum Lösen linearer Gleichungssysteme mithilfe eines auf der Graphentheorie basierenden Algorithmus erheblich verkürzen lässt.

Es ist für die Verwendung mit Daten optimiert, die eine spärliche Struktur aufweisen (dh nicht mehr als 10% Koeffizienten ungleich Null in den Gleichungen enthalten), und zeigt im Durchschnitt und im besten Fall die Asymptotik Θ (n⋅log (n) ⋅log (n)), wobei n ist Die Anzahl der Variablen und im schlimmsten Fall (wenn das System zu ~ 100% voll ist) ist sein asymptotisches Verhalten mit klassischen Algorithmen vergleichbar (Θ (n ³ )). Darüber hinaus zeigt der Algorithmus auf Systemen mit ~ 10 ⁵ Unbekannten eine hundertfache Beschleunigung im Vergleich zu solchen, die in speziellen Bibliotheken für lineare Algebra (z. B. Superlu oder Lapack ) implementiert sind .


Wichtig: Der Artikel und der beschriebene Algorithmus erfordern ein Verständnis der linearen Algebra und der Graphentheorie im ersten Studienjahr einer Universität.

Darstellung der SLAE als Grafik

Betrachten Sie das einfachste spärliche System linearer Gleichungen:


Achtung: Das System wird zufällig generiert und später zur Demonstration der Schritte des Algorithmus verwendet

Auf den ersten Blick entsteht eine Assoziation mit einem anderen mathematischen Objekt - der Graph-Adjazenz-Matrix. Warum also nicht die Daten in Adjazenzlisten konvertieren, RAM zur Laufzeit sparen und den Zugriff auf Koeffizienten ungleich Null beschleunigen?

Dazu reicht es aus, die Matrix zu transponieren und die Invariante „A [i] [j] = z establish die i-te Variable gibt die j-te Gleichung mit dem Koeffizienten z ein“ zu erstellen und dann für jede Nicht-Null A [i] [j] die entsprechende Kante zu konstruieren vom Scheitelpunkt i zum Scheitelpunkt j.

Das resultierende Diagramm sieht folgendermaßen aus:



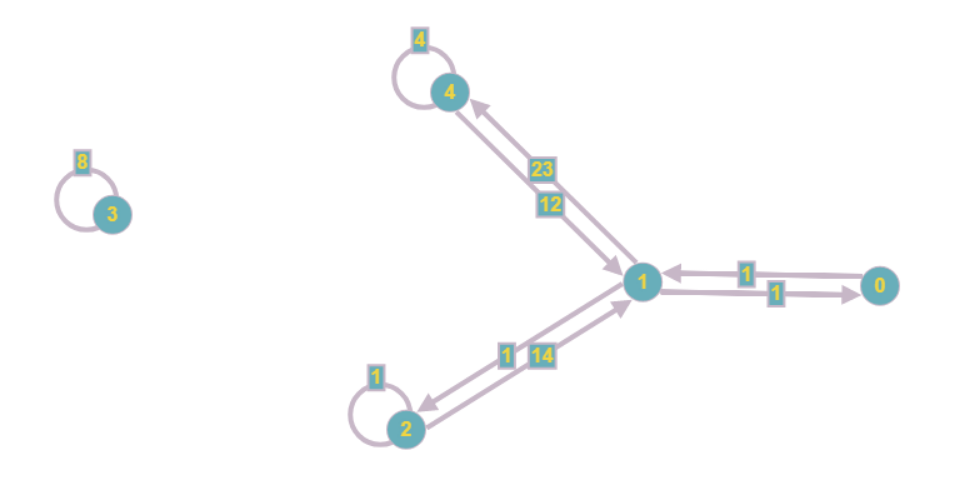
Selbst visuell stellt sich heraus, dass es weniger umständlich ist und die asymptotischen Speicherkosten von O (n ² ) auf O (n + m) sinken, wobei m die Anzahl der Koeffizienten im System ist.

Isolierung schwach verbundener Komponenten

Die zweite algorithmische Idee, die bei der Betrachtung der resultierenden Entität in den Sinn kommt: die Verwendung des Prinzips „Teilen und Erobern“. In Bezug auf den Graphen führt dies zur Trennung des Satzes von Eckpunkten in schwach verbundene Komponenten.

Ich möchte Sie daran erinnern, dass die schwach verbundene Komponente eine solche Teilmenge von Scheitelpunkten ist, die maximal eingeschlossen ist, dass zwischen zwei beliebigen Punkten ein Pfad von Kanten in einem ungerichteten Diagramm existiert. Wir können einen ungerichteten Graphen aus dem ursprünglichen erhalten, indem wir beispielsweise jeder Kante das Gegenteil hinzufügen (mit anschließender Entfernung). Dann enthält ein Scheitelpunkt der Verbindung alle Scheitelpunkte, die wir erreichen können, wenn wir den Graphen in der Tiefe umrunden.

Nach der Trennung der schwach verbundenen Komponenten hat der Graph die folgende Form:



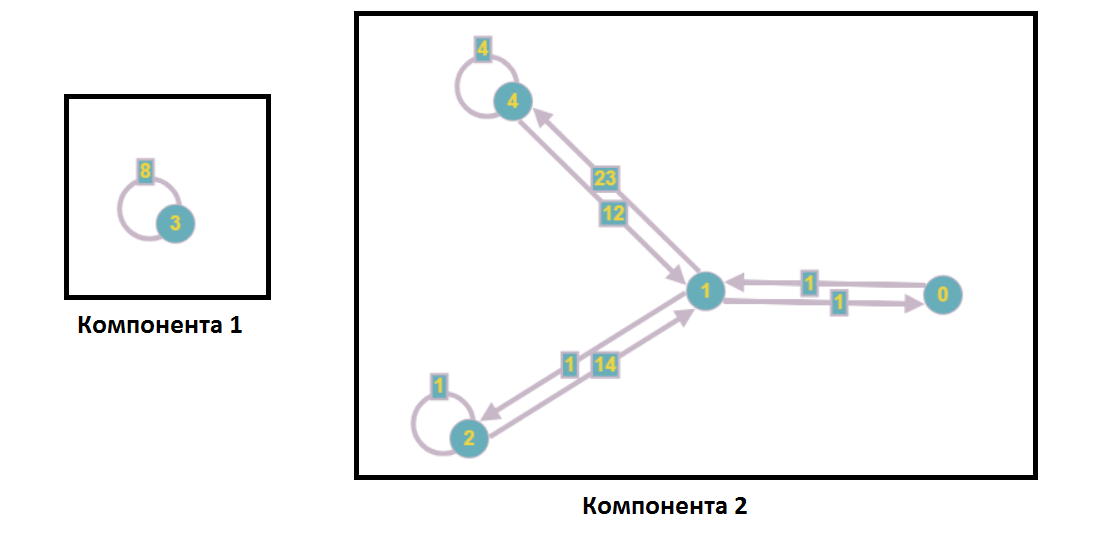
Im Rahmen der Analyse eines linearen Gleichungssystems bedeutet dies, dass kein einziger Scheitelpunkt aus der ersten Komponente in den Gleichungen mit den Zahlen der zweiten Komponente enthalten ist und umgekehrt, dh wir können diese Subsysteme unabhängig voneinander lösen (z. B. parallel).

Scheitelpunktreduzierung

Der nächste Schritt des Algorithmus ist genau die Optimierung für die Arbeit mit spärlichen Matrizen. Selbst in der Grafik aus dem Beispiel gibt es "hängende" Peaks, was bedeutet, dass einige der Gleichungen nur einen Unbekannten enthalten und der Wert dieses Unbekannten bekanntlich leicht zu finden ist.

Um solche Gleichungen zu bestimmen, wird vorgeschlagen, ein Array von Listen zu speichern, die die Anzahl der in der Gleichung enthaltenen Variablen mit der Nummer dieses Array-Elements enthalten. Wenn die Liste die Einheitsgröße erreicht, können wir den „einzigen“ Scheitelpunkt reduzieren und den Rest der Gleichungen in den anderen Gleichungen, in die dieser Scheitelpunkt eingeht, informieren.

Somit können wir den Scheitelpunkt 3 unmittelbar nach der vollständigen Verarbeitung der Komponente aus dem Beispiel reduzieren:

$$

$$8⋅_3 = 4⇒_3 = 1/2$$

Ähnlich verfahren wir mit Gleichung 0, da sie nur eine Variable enthält:

$$

$$1⋅x_1 = 1⇒x_1 = 1$$

Andere Gleichungen ändern sich ebenfalls, nachdem dieses Ergebnis gefunden wurde:

$$$$ display $$ 1⋅_1 ​​+ 1⋅_2 = 3⇒1⋅_2 = 3-1 = 2 $$ display $$

Das Diagramm hat die folgende Form:



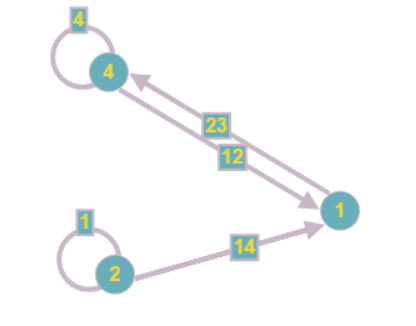
Beachten Sie, dass beim Reduzieren eines Scheitelpunkts möglicherweise auch andere angezeigt werden, die ebenfalls einen unbekannten enthalten. Daher sollte dieser Schritt des Algorithmus wiederholt werden, bis mindestens einer der Eckpunkte reduziert werden kann.

Graph neu erstellen

Die aufmerksamsten Leser könnten feststellen, dass eine Situation möglich ist, in der jeder der Scheitelpunkte des Diagramms einen Grad von mindestens zwei aufweist und es unmöglich ist, die Scheitelpunkte weiterhin konsequent zu reduzieren.

Das einfachste Beispiel für einen solchen Graphen: Jeder Scheitelpunkt hat einen Auftrittsgrad von zwei, keiner der Scheitelpunkte kann reduziert werden.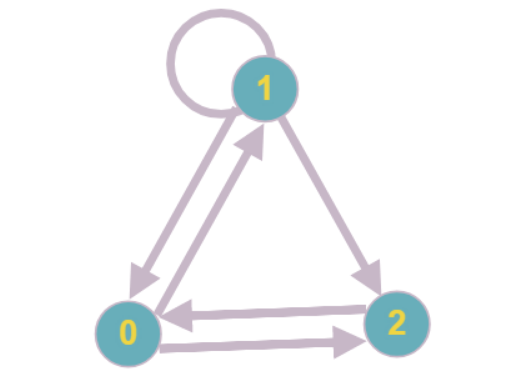



Im Rahmen der Optimierung für dünn besetzte Matrizen wird davon ausgegangen, dass solche Untergraphen klein sind. Sie müssen jedoch noch mit ihnen arbeiten. Um die Werte der Unbekannten zu berechnen, die Teil des Gleichungssystems sind, wird vorgeschlagen, klassische Methoden zur Lösung von SLAEs zu verwenden (aus diesem Grund zeigt die Einführung, dass unser Algorithmus für eine Matrix, in der alle oder fast alle Koeffizienten in den Gleichungen ungleich Null sind, dieselbe asymptotische Komplexität aufweist wie die Standardkoeffizienten )

Sie können beispielsweise die nach der Reduktion verbleibenden Scheitelpunkte wieder in die Matrixform bringen und die Gauß-Methode zum Lösen von SLAEs darauf anwenden . Auf diese Weise erhalten wir die genaue Lösung, und die Geschwindigkeit des Algorithmus wird verringert, da nicht das gesamte System, sondern nur ein Teil davon verarbeitet wird.

Algorithmus testen

Um die Software-Implementierung des Algorithmus zu testen, haben wir mehrere reale Gleichungssysteme mit großem Volumen sowie eine große Anzahl zufällig generierter Systeme verwendet.
Die Erzeugung eines zufälligen Gleichungssystems erfolgte durch sequentielles Hinzufügen von Kanten beliebigen Gewichts zwischen zwei zufälligen Eckpunkten. Insgesamt war das System zu 5-10% voll. Die Richtigkeit der Lösungen wurde überprüft, indem die erhaltenen Antworten in das ursprüngliche Gleichungssystem eingesetzt wurden.


Die Systeme reichten von 1.000 bis 200.000 Unbekannten

Um die Leistung zu vergleichen, haben wir die beliebtesten Bibliotheken zur Lösung linearer Algebra-Probleme wie Superlu und Lapack verwendet. Natürlich konzentrieren sich diese Bibliotheken auf die Lösung einer Vielzahl von Problemen, und die Lösung von SLAE in ihnen ist in keiner Weise optimiert, sodass sich der Geschwindigkeitsunterschied als signifikant herausstellte.


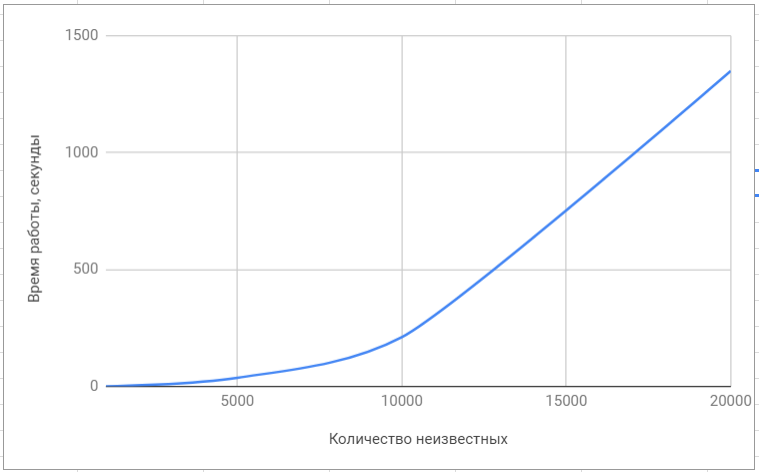Testen der Lapack-Bibliothek


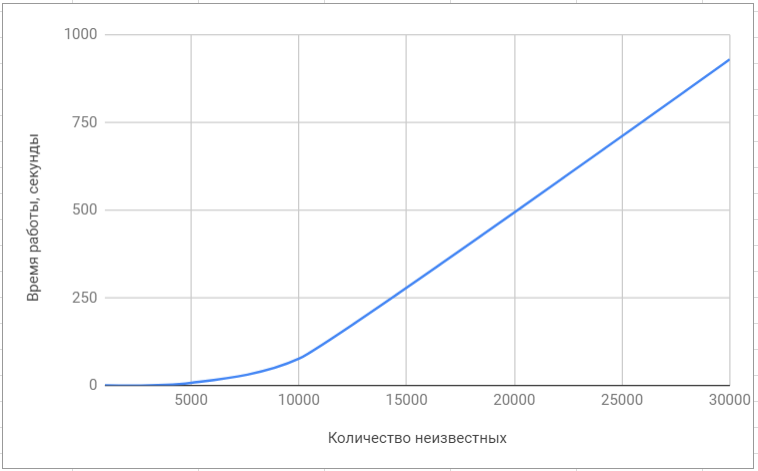Testen der Bibliothek 'superlu'

Hier ist der endgültige Vergleich unseres Algorithmus mit den in gängigen Bibliotheken implementierten Algorithmen:

Fazit

Auch wenn Sie kein Entwickler von 1C: Enterprise-Konfigurationen sind, können Sie die in diesem Artikel beschriebenen Ideen und Optimierungsmethoden nicht nur bei der Implementierung eines Algorithmus zur Lösung von SLAEs verwenden, sondern auch für eine ganze Klasse von linearen Algebra-Problemen, die mit Matrizen verbunden sind.

Für 1C-Entwickler fügen wir hinzu, dass die neue Funktionalität der SLAE-Lösung die parallele Verwendung von Computerressourcen unterstützt und Sie die Anzahl der verwendeten Berechnungsthreads anpassen können.