Richard Hamming: Kapitel 20. Modellierung - III

"Das Ziel dieses Kurses ist es, Sie auf Ihre technische Zukunft vorzubereiten."

Es bleiben noch 2 Kapitel zu veröffentlichen ...

Modellierung - III

Ich werde die im vorherigen Kapitel angegebene allgemeine Richtung fortsetzen, aber dieses Mal werde ich mich auf den alten Ausdruck „Müll rein - Müll raus“ konzentrieren, der oft als GIGO (Müll rein, Müll raus) abgekürzt wird. Die Idee ist, dass Sie nur falsche Ergebnisse erhalten können, wenn Sie ungenau gesammelte Daten und falsch definierte Ausdrücke in die Eingabe einfügen. Implizit wird auch das Gegenteil angenommen: Aus der Verfügbarkeit genauer Eingabedaten wird das richtige Ergebnis erhalten. Ich werde zeigen, dass diese beiden Annahmen falsch sein können.

Häufig basiert die Modellierung auf der Lösung von Differentialgleichungen. Daher betrachten wir zunächst die einfachste Differentialgleichung erster Ordnung der Form



Wie Sie sich erinnern, besteht das Richtungsfeld aus den Linien, die an jedem Punkt der xy-Ebene mit den durch die Differentialgleichung gegebenen Winkelkoeffizienten konstruiert wurden (Abbildung 20.I). Zum Beispiel hat eine Differentialgleichung ein in Abbildung 20.II gezeigtes Richtungsfeld.





Abbildung 20.I.

Für jeden konzentrischen Kreis



so dass die Steigung der Linie immer gleich ist und vom Wert von k abhängt. Solche Kurven werden Isoklinen genannt .

Betrachten wir nun das Richtungsfeld einer anderen Differentialgleichung (Abbildung 20.III). Auf der linken Seite sehen wir ein divergierendes Richtungsfeld, was bedeutet, dass kleine Änderungen der Anfangswerte oder kleine Berechnungsfehler zu einem großen Unterschied in den Werten in der Mitte des Pfades führen. Auf der rechten Seite sehen wir, dass das Richtungsfeld konvergiert. Dies bedeutet, dass bei einem größeren Unterschied in der Mitte des Pfads der Unterschied in den Werten am rechten Ende gering ist. Dieses einfache Beispiel zeigt, wie kleine Fehler groß, große Fehler klein und darüber hinaus wie kleine Fehler groß und dann wieder klein werden können. Daher hängt die Genauigkeit der Lösung von dem spezifischen Intervall ab, in dem die Lösung berechnet wird. Es gibt keine absolute allgemeine Genauigkeit.



Abbildung 20.II.



Abbildung 20.III

Diese Überlegungen dienen der Funktion


Das ist eine Lösung für die Differentialgleichung



Sie haben sich wahrscheinlich ein „Rohr“ vorgestellt, das sich zuerst ausdehnt und dann um die „wahre, exakte Lösung“ der Gleichung verengt. Diese Darstellung ist perfekt für den Fall von zwei Messungen, aber wenn ich ein System von n solchen Differentialgleichungen habe - 28 im Fall des zuvor erwähnten Abfangraketenproblems für die Marine -, dann erweisen sich diese „Rohre“ um die wahre Lösung der Gleichung als nicht so, wie sie scheinen auf den ersten Blick. Eine Figur, die aus vier Kreisen in zwei Dimensionen besteht, führt zu dem in Kapitel 9 beschriebenen Paradoxon der n-Dimensionen für den zehndimensionalen Raum. Dies ist nur eine weitere Ansicht des im vorherigen Kapitel beschriebenen Problems der stabilen und instabilen Modellierung. Dieses Mal werde ich spezifische Beispiele für Differentialgleichungen geben.

Wie lösen wir Differentialgleichungen numerisch? Ausgehend von der üblichen Differentialgleichung erster Ordnung zeichnen wir ein Richtungsfeld. Unsere Aufgabe ist es, einen bestimmten Anfangswert den Wert am nächstgelegenen Punkt von Interesse berechnen zu lassen. Wenn wir den lokalen Steigungskoeffizienten der durch die Differentialgleichung gegebenen Linie nehmen und einen kleinen Schritt vorwärts entlang der Tangente machen, führen wir nur einen kleinen Fehler ein (Abbildung 20.IV).

Mit diesem neuen Punkt bewegen wir uns zum nächsten Punkt, aber wie in der Abbildung zu sehen ist, weichen wir allmählich von der wahren Kurve ab, da wir den Steigungskoeffizienten des vorherigen Schritts und nicht den wahren Steigungskoeffizienten für das aktuelle Intervall verwenden. Um diesen Effekt zu vermeiden, „prognostizieren“ wir einen bestimmten Wert, schätzen den Winkelkoeffizienten an diesem Punkt (unter Verwendung der Differentialgleichung) und verwenden dann den Durchschnittswert des Winkelkoeffizienten an den beiden Grenzen des Intervalls als Winkelkoeffizienten für dieses Intervall.

Mit dieser gemittelten Steigung gehen wir dann noch einen Schritt weiter, diesmal mit der Formel „Korrektur“. Wenn die mit den Formeln "Prognose" und "Korrektur" erhaltenen Werte nahe genug sind, gehen wir davon aus, dass unsere Berechnungen genau genug sind, andernfalls müssen wir die Schrittgröße reduzieren. Wenn der Unterschied zwischen den Werten zu gering ist, müssen wir die Schrittgröße erhöhen. Somit hat das traditionelle Prädiktor-Korrektor-Schema einen eingebauten Mechanismus zum Überprüfen von Fehlern bei jedem Schritt, aber dieser Fehler bei einem bestimmten Schritt ist in keiner Weise und in keiner Weise ein allgemeiner akkumulierter Fehler! Es ist absolut klar, dass der akkumulierte Fehler davon abhängt, ob das Richtungsfeld konvergiert oder divergiert.



Abbildung 20.IV.



Abbildung 20.V.

Wir haben sowohl für den Prognoseschritt als auch für den Korrekturschritt einfache gerade Linien verwendet. Die Verwendung von Polynomen höheren Grades liefert ein genaueres Ergebnis. Üblicherweise werden Polynome mit viertel Grad verwendet (die Lösung von Differentialgleichungen nach der Adams-Bashfort-Methode, der Milne-Methode, der Hamming-Methode usw.). Daher müssen wir die Werte der Funktion und ihrer Ableitungen an mehreren vorherigen Punkten verwenden, um den Wert der Funktion am nächsten Punkt vorherzusagen. Danach verwenden wir die Substitution dieses Werts in der Differentialgleichung und approximieren den neuen Wert des Winkelkoeffizienten. Mit den neuen und vorherigen Werten des Winkelkoeffizienten sowie den Werten der gewünschten Funktion korrigieren wir den erhaltenen Wert. Es ist an der Zeit zu bemerken, dass der Korrektor nichts anderes als ein digitaler rekursiver Filter ist, bei dem die Eingabewerte Ableitungen und die Ausgabewerte die Werte der gewünschten Funktion sind.

Stabilität und andere zuvor diskutierte Konzepte bleiben relevant. Wie bereits erwähnt, gibt es eine zusätzliche Rückkopplungsschleife für die vorhergesagte Lösung der Differentialgleichung, die wiederum zur Berechnung des eingestellten Winkelkoeffizienten verwendet wird. Beide Werte werden zur Lösung der Differentialgleichung verwendet, rekursive digitale Filter sind nur Formeln und nichts weiter. Sie sind jedoch keine Übertragungseigenschaften, wie sie üblicherweise in der Theorie der digitalen Filter berücksichtigt werden. In diesem Fall erfolgt die Berechnung der Werte der Differentialgleichung einfach. In diesem Fall ist der Unterschied zwischen den Ansätzen signifikant: In digitalen Filtern wird das Signal linear verarbeitet, während beim Lösen von Differentialgleichungen eine Nichtlinearität vorliegt, die durch Berechnung der Werte der Ableitungen der Funktion eingeführt wird. Dies ist nicht dasselbe wie ein digitaler Filter.

Wenn Sie ein System von n Differentialgleichungen lösen, haben Sie es mit einem Vektor von n Komponenten zu tun. Sie sagen den nächsten Wert jeder Komponente voraus, bewerten jede der n Ableitungen, passen jeden der vorhergesagten Werte an und akzeptieren dann das Berechnungsergebnis in diesem Schritt oder lehnen es ab, wenn der lokale Fehler zu groß ist. Sie neigen dazu, kleine Fehler als „Pipe“ zu betrachten, die einen tatsächlich berechneten Pfad umgibt. Und noch einmal, ich fordere Sie auf, sich an das Paradoxon der vier Kreise in hochdimensionalen Räumen zu erinnern. Solche "Pfeifen" sind möglicherweise nicht das, was sie auf den ersten Blick scheinen.

Lassen Sie mich nun auf den signifikanten Unterschied zwischen den beiden Ansätzen hinweisen: Berechnungsmethoden und Theorie der digitalen Filter. In gängigen Lehrbüchern werden nur Methoden der Computermathematik beschrieben, die Funktionen durch Polynome approximieren. Rekursive Filter verwenden Frequenzen in Bewertungsformeln! Dies führt zu signifikanten Unterschieden!

Um den Unterschied zu sehen, stellen wir uns vor, wir entwickeln einen Simulator für eine menschliche Landung auf dem Mars. Der klassische Ansatz konzentriert sich auf die Form der Landebahn und verwendet die Polynomnäherung für lokale Regionen. Der resultierende Pfad weist Unterbrechungspunkte bei der Beschleunigung auf, wenn wir uns Schritt für Schritt von Intervall zu Intervall bewegen. Im Fall des Frequenzansatzes werden wir uns darauf konzentrieren, die richtigen Frequenzen zu erhalten und den Ort so zu lassen, wie er sich herausstellt. Im Idealfall sind beide Trajektorien gleich, in der Praxis können sie sich jedoch erheblich unterscheiden.

Welche Wanderung soll ich machen? Je mehr Sie darüber nachdenken, desto eher glauben Sie, dass der Pilot im Simulator ein „Gefühl“ für das Verhalten des Landemoduls erhalten möchte, und es scheint, dass der Frequenzgang des Simulators vom Piloten gut „gefühlt“ werden sollte. Wenn sich der Ort geringfügig unterscheidet, gleicht die Rückkopplungsschleife diese Abweichung während des Landevorgangs aus. Wenn sich das „Gefühl“ der Steuerung während des realen Flugs unterscheidet, ist der Pilot besorgt über neue „Empfindungen“, die nicht im Simulator vorhanden waren. Es schien mir immer, dass Simulatoren Piloten so gut wie möglich auf echte Empfindungen vorbereiten sollten (natürlich können wir die niedrige Schwerkraft auf dem Mars nicht lange simulieren), damit sie sich wohl fühlen, wenn sie in Wirklichkeit auf eine Situation stoßen, mit der sie konfrontiert sind wiederholt im Simulator angetroffen. Leider wissen wir zu wenig darüber, was der Pilot "fühlt". Erfasst der Pilot nur die tatsächlichen Frequenzen aus der Fourier-Erweiterung oder erfasst er auch die komplexen verblassenden Laplace-Frequenzen (oder sollten wir Wavelets verwenden?). Fühlen verschiedene Piloten das Gleiche? Wir müssen mehr als jetzt über diese wesentlichen Entwurfsbedingungen wissen.

Die oben beschriebene Situation ist ein Standardwiderspruch zwischen dem mathematischen und dem technischen Ansatz zur Lösung des Problems. Diese Ansätze haben unterschiedliche Ziele bei der Lösung von Differentialgleichungen (wie bei vielen anderen Problemen), daher führen sie zu unterschiedlichen Ergebnissen. Wenn Sie mit der Modellierung aufwarten, werden Sie feststellen, dass es versteckte Nuancen gibt, die sich in der Praxis als sehr wichtig herausstellen, von denen die Mathematiker jedoch nichts wissen und die Konsequenzen ihrer Vernachlässigung in jeder Hinsicht leugnen. Schauen wir uns zwei Pfade an (Abbildung 20.IV), die ich grob geschätzt habe. Die obere Kurve beschreibt den Ort genauer, aber die Biegungen geben ein völlig anderes "Gefühl" als die reale Welt, die zweite Kurve ist im Ort fehlerhafter, hat aber eine größere Genauigkeit in Bezug auf das "Gefühl". Ich habe erneut deutlich gezeigt, warum ich glaube, dass eine Person mit einem tiefen Verständnis des Themenbereichs des Problems auch die mathematischen Methoden zur Lösung des Problems verstehen und sich nicht auf traditionelle Lösungsmethoden verlassen sollte.

Jetzt möchte ich eine andere Geschichte über die frühen Tage des Testens des Nike-Raketenabwehrsystems erzählen. Zu dieser Zeit fanden in White Sands Feldversuche statt, die auch als „Feldtelefontest“ bezeichnet wurden. Dies waren Teststarts, bei denen die Rakete einer vorgegebenen Flugbahn folgen und im letzten Moment explodieren musste, damit die gesamte Energie der Explosion nicht über die Grenzen eines bestimmten Gebiets hinausging und mehr Schaden verursachte, was einem milderen Tropfen einzelner Teile der Rakete auf dem Boden vorzuziehen war angeblich hätte weniger Schaden anrichten sollen. Ziel der Tests war es, reale Messungen von Auftrieb und Luftwiderstand als Funktion der Flughöhe und -geschwindigkeit zu erhalten, um das Design zu debuggen und zu verbessern.

Als ich meinen Freund traf, der von den Tests zurückgekehrt war, wanderte er durch die Korridore der Bell Laboratories und sah ziemlich elend aus. Warum? Weil die ersten beiden der sechs geplanten Starts mitten im Flug fehlschlugen und niemand wusste warum. Die für die weiteren Entwurfsphasen erforderlichen Daten waren nicht verfügbar, was schwerwiegende Probleme für das gesamte Projekt bedeutete. Ich sagte, wenn er mir Differentialgleichungen zur Verfügung stellen kann, die den Flug beschreiben, kann ich das Mädchen dazu bringen, sie zu lösen (der Zugang zu großen Computern war Ende der 1940er Jahre nicht einfach). Nach ungefähr einer Woche lieferten sie sieben Differentialgleichungen erster Ordnung und das Mädchen war bereit zu beginnen. Aber wie waren die Anfangsbedingungen einen Moment vor Beginn der Flugprobleme? (Damals hatten wir nicht genug Rechenleistung, um die gesamte Flugbahn schnell zu berechnen.) Sie wussten es nicht! Telemetriedaten waren einen Moment vor dem Ausfall unverständlich. Ich war nicht überrascht und es hat mich nicht gestört. Also haben wir die geschätzten Werte für Höhe, Fluggeschwindigkeit, Anstellwinkel usw. verwendet. - eine Anfangsbedingung für jede der Variablen, die den Flugweg beschreiben. Mit anderen Worten, ich hatte Müll am Eingang. Aber früher wurde mir klar, dass die von uns simulierten Feldtests so beschaffen waren, dass kleine Abweichungen von der vorgeschlagenen Flugbahn vom Leitsystem automatisch korrigiert wurden! Ich hatte es mit einem sehr konvergierenden Feld von Richtungen zu tun.

Wir fanden heraus, dass die Rakete entlang der Quer- und Vertikalachse stabil war, aber als sich eine von ihnen stabilisierte, führte ein Energieüberschuss zu Schwingungen entlang der anderen Achse. Somit gab es nicht nur Schwingungen entlang der Quer- und Vertikalachse, sondern auch eine periodische Übertragung zunehmender Energie zwischen ihnen, die durch die Drehung der Rakete um ihre Längsachse verursacht wurde. Sobald die berechneten Kurven für einen kleinen Teil der Flugbahn demonstriert wurden, wurde allen sofort klar, dass die Kreuzstabilisierung nicht berücksichtigt wurde, und jeder wusste, wie man sie repariert. So haben wir eine Lösung erhalten, die es uns auch ermöglicht, die während der Tests erhaltenen verdorbenen Telemetriedaten zu lesen und den Zeitraum der Energieübertragung zu klären - tatsächlich die richtigen Differentialgleichungen für die Berechnungen bereitzustellen. Ich hatte ein wenig Arbeit, außer um sicherzustellen, dass das Mädchen mit dem Desktop-Rechner ehrlich alles berechnete. Im Mai bestand das Verdienst darin, zu verstehen, dass (1) wir simulieren können, was passiert ist (jetzt ist es eine Routine bei der Untersuchung von Unfällen, aber dann war es eine Innovation) und (2) das Richtungsfeld konvergiert, sodass die Anfangsbedingungen möglicherweise nicht genau spezifiziert werden.

Ich habe Ihnen diese Geschichte erzählt, um zu zeigen, dass das GIGO-Prinzip nicht immer funktioniert. Eine ähnliche Geschichte passierte mir während einer frühen Bombensimulation in Los Alamos. Allmählich wurde mir klar, dass unsere Berechnungen, die für die Zustandsgleichung erstellt wurden, auf ziemlich ungenauen Daten basierten. Die Zustandsgleichung bezieht sich auf den Druck und die Dichte einer Substanz (auch die Temperatur, aber ich werde sie in diesem Beispiel weglassen). Daten aus Hochdrucklabors, Annäherungen aus der Untersuchung von Erdbeben, der Sternkerndichte und der asymptotischen Theorie des unendlichen Drucks wurden als Punkte auf einem sehr großen Millimeterpapier dargestellt (Abbildung 20.VII). Dann zeichneten wir mithilfe von Mustern Kurven, die die gestreuten Punkte verbanden. Basierend auf diesen Kurven haben wir dann Tabellen mit Funktionswerten mit einer Genauigkeit von 3 Dezimalstellen erstellt. Dies bedeutet, dass wir einfach 0 oder 5 als 4. Dezimalstelle angenommen haben. Wir haben diese Daten verwendet, um Tabellen bis zur 5. und 6. Dezimalstelle zu erstellen. Basierend auf diesen Tabellen wurden unsere weiteren Berechnungen erstellt. Zu dieser Zeit war ich, wie ich bereits erwähnte, eine Art Taschenrechner, und meine Aufgabe war es, die Physiker zu zählen und dadurch von diesem Beruf zu befreien, damit sie ihre Arbeit erledigen können.



Abbildung 20.VII

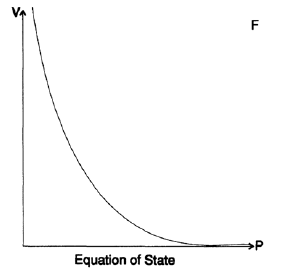
Nach Kriegsende blieb ich noch ein halbes Jahr in Los Alamos, und einer der Gründe dafür war, dass ich verstehen wollte, wie solche ungenauen Daten zu einer so genauen Simulation des endgültigen Entwurfs führen können. Ich habe lange darüber nachgedacht und die Antwort gefunden. In der Mitte der Berechnungen haben wir endliche Differenzen zweiter Ordnung verwendet. Die Differenz erster Ordnung zeigte den Wert der Kraft auf einer Seite jeder Schale, und die Unterschiede der auf beiden Seiten benachbarten Schalen ergaben die resultierende Kraft, die die Schale bewegt. Wir mussten dünne Schalen verwenden, also subtrahierten wir Zahlen sehr nahe beieinander und mussten viele Nachkommastellen verwenden. Weitere Studien zeigten, dass sich die Schale beim Explodieren des „Dings“ entlang der Kurve nach oben bewegte und sich wahrscheinlich manchmal teilweise zurückschob, sodass jeder lokale Fehler in der Zustandsgleichung nahe am Durchschnittswert lag. Es war wirklich wichtig, die Krümmung der Zustandsgleichung zu ermitteln, und wie bereits erwähnt, sollte sie im Durchschnitt genau sein. Somit entsteht Müll in der Eingabe, aber genauer als je zuvor Ausgabeergebnisse!

Diese drei Beispiele zeigen, was zuvor implizit erwähnt wurde. Wenn es eine Rückkopplungsschleife für die im Problem verwendeten Variablen gibt, ist es nicht erforderlich, deren Werte genau zu kennen. Auf dieser Grundlage die bemerkenswerte Idee von G.S. Black, wie eine Rückkopplungsschleife in Verstärkern aufgebaut werden kann (Abbildung 20.VIII): Solange die Verstärkung sehr hoch ist, muss nur der Widerstand eines Widerstands genau angepasst werden, alle anderen Teile können mit geringer Genauigkeit implementiert werden. Für die in Abbildung 20.VIII gezeigte Schaltung erhalten wir die folgenden Ausdrücke:



Abbildung 20.VIII

Wie Sie sehen können, konzentriert sich fast die gesamte Messunsicherheit auf einen Widerstand mit einem Nennwert von 1/10, während der Transmissionskoeffizient möglicherweise ungenau ist. Die Rückkopplungsschleife von Black ermöglicht es uns, genaue Dinge aus ungenauen Teilen zu erstellen.



Jetzt sehen Sie, warum ich Ihnen keine elegante Formel geben kann, die für alle Gelegenheiten geeignet ist. Es sollte davon abhängen, welche Berechnungen für bestimmte Mengen durchgeführt werden. Werden ungenaue Werte eine Rückkopplungsschleife durchlaufen, die den Fehler kompensiert, oder werden Fehler ohne Rückkopplungsschutz außerhalb des Systems auftreten? Wenn für die Variablen keine Rückmeldung erfolgt, ist es wichtig, ihre genauen Werte zu erhalten.
Das Bewusstsein für diese Tatsache kann sich also auf das Design des Systems auswirken! Ein gut konzipiertes System schützt Sie vor der Verwendung einer großen Anzahl von Präzisionskomponenten. Solche Gestaltungsprinzipien werden derzeit jedoch noch missverstanden und erfordern sorgfältiges Studium. Und der Punkt ist nicht, dass gute Designer dies auf der Ebene der Intuition nicht verstehen, es ist einfach nicht so einfach, diese Prinzipien in den von Ihnen untersuchten Entwurfsmethoden anzuwenden. Gute Köpfe brauchen immer noch alle automatisierten Designtools, die wir entwickelt haben. Die besten Köpfe werden in der Lage sein, diese Prinzipien in die untersuchten Entwurfsmethoden zu integrieren, um sie für alle anderen „out of the box“ zugänglich zu machen.

Wenden wir uns nun einem anderen Beispiel und Prinzip zu, das es mir ermöglichte, eine Lösung für ein wichtiges Problem zu finden. Ich erhielt eine Differentialgleichung



Es fällt sofort auf, dass der Wert der Bedingung im Unendlichen tatsächlich die rechte Seite der Differentialgleichung ist, die gleich Null ist (Abbildung 20.IX). Schauen

wir uns jedoch das Problem der Stabilität an. Wenn der Wert von y an einem ausreichend entfernten Punkt x groß genug wird, wird der Wert von sinh ( y ) viel größer, die zweite Ableitung nimmt einen großen positiven Wert an und die Kurve schießt in Richtung plus unendlich. Ebenso, wenn yzu klein, dann schießt die Kurve in Richtung minus unendlich. Und es spielt überhaupt keine Rolle, ob wir uns von links nach rechts oder von rechts nach links bewegen. Früher, als ich auf ein divergierendes Feld von Richtungen stieß, benutzte ich den offensichtlichen Trick: Ich integrierte in die entgegengesetzte Richtung und bekam die genaue Lösung. Aber in diesem Fall sind wir wie auf dem Kamm einer Sanddüne und sobald beide Beine am selben Hang sind, brechen wir zusammen.



Abbildung 20.IX

Ich habe versucht, die Erweiterung in Potenzreihen zu verwenden, wobei die Erweiterung in Nicht-Leistungsreihen sich der ursprünglichen Kurve annähert , aber das Problem ist nicht verschwunden, insbesondere bei großen Werten von k. Weder ich noch meine Freunde konnten eine angemessene Lösung anbieten. Dann ging ich zu den Problemleitern und begann zunächst, die Randbedingung im Unendlichen zu bestreiten. Es stellte sich jedoch heraus, dass diese Bedingung mit dem in den Schichten der Moleküle gemessenen Abstand zusammenhängt, und zu diesem Zeitpunkt hatte jeder praktisch realisierbare Transistor eine nahezu unendliche Anzahl von Schichten. Dann fing ich an, die Gleichung zu bestreiten, und sie gewannen erneut das Argument, und ich musste in mein Büro zurücktreten und weiter nachdenken.

Dies war eine wichtige Aufgabe im Zusammenhang mit dem Design und dem Verständnis der zu dieser Zeit entwickelten Transistoren. Ich habe immer argumentiert, dass ich eine Lösung finden kann, wenn die Aufgabe wichtig und richtig gestellt ist. Deshalb hatte ich keine Wahl, es war eine Ehrensache.

Ich brauchte einige Tage zum Nachdenken, um zu erkennen, dass Instabilität der Schlüssel zu einer geeigneten Methode war. Ich habe die Lösung der Differentialgleichung in einem kleinen Intervall mit dem Differentialanalysator erstellt, den ich zu diesem Zeitpunkt hatte, und wenn die Lösung hochgeschossen ist, bedeutet dies, dass ich zu viel Winkelkoeffizienten gewählt habe, wenn sie abgeschossen hat, dann habe ich auch gewählt kleiner Wert. So ging ich mit kleinen Schritten den Kamm der Düne entlang, und sobald die Entscheidung auf einer Seite fiel, wusste ich, was getan werden musste, um wieder auf den Kamm zu gelangen. Wie Sie sehen, ist professioneller Stolz ein guter Helfer, wenn Sie unter schwierigen Bedingungen eine Lösung für eine wichtige Aufgabe finden müssen. Wie einfach es war, sich zu weigern, dieses Problem zu lösen, sich auf die Tatsache zu beziehen, dass es unlösbar war,falsch gestellt oder andere Ausreden gefunden, aber ich glaube immer noch, dass wichtige und richtig gestellte Aufgaben es Ihnen ermöglichen, neue nützliche Informationen zu erhalten. Eine Reihe von Problemen im Zusammenhang mit der Raumladung, die ich mithilfe von Berechnungsmethoden gelöst habe, hatten eine ähnliche Komplexität, die mit Instabilität in beide Richtungen verbunden war.

Bevor ich Ihnen die folgende Geschichte erzähle, möchte ich Sie an den Rorschach-Test erinnern, der in meiner Jugend beliebt war. Ein Tropfen Tinte wird auf ein Blatt Papier aufgetragen, wonach es in zwei Hälften gefaltet wird, und wenn es wieder ausgepackt wird, wird ein symmetrischer Fleck mit einer ziemlich zufälligen Form erhalten. Die Reihenfolge dieser Blots wird Probanden gezeigt, die gebeten werden, zu sagen, was sie sehen. Ihre Antworten werden verwendet, um die "Merkmale" ihrer Persönlichkeit zu analysieren. Offensichtlich sind die Antworten eine Erfindung ihrer Vorstellungskraft, da der Punkt im Wesentlichen eine zufällige Form hat. Es ist, als würde man Wolken am Himmel betrachten und darüber diskutieren, wie sie aussehen. Sie diskutieren nur die Früchte Ihrer Vorstellungskraft, nicht die Realität, und dies eröffnet in gewissem Maße neue Dinge über sich selbst, nicht über die Wolken. Ich schlage vor, dass die Tintenfleckmethode nicht mehr verwendet wird.

Und jetzt kommen wir zur Geschichte selbst. Einmal baute mein Freund als Psychologe von Bella Laboratories ein Auto mit 12 Schaltern und zwei Glühbirnen - rot und grün. Sie stellten die Schalter ein, drückten die Taste und dann ging ein rotes oder grünes Licht an. Nachdem das erste Thema 20 Versuche unternommen hatte, schlug er eine Theorie zum Anzünden einer grünen Glühbirne vor. Diese Theorie wurde an das nächste Opfer weitergegeben, wonach sie 20 Versuche unternahm, ihre Theorie zum Anzünden einer grünen Glühbirne vorzuschlagen. Und so weiter bis ins Unendliche. Ziel des Experiments war es zu untersuchen, wie sich Theorien entwickeln.

Aber mein Freund, der in seinem eigenen Stil handelte, verband die Glühbirnen mit einer zufälligen Signalquelle! Einmal beschwerte er sich bei mir, dass kein einziger Teilnehmer des Experiments (und alle waren hochkarätige Forscher der Bell Laboratories) sagte, dass es kein Muster gebe. Ich schlug sofort vor, dass keiner von ihnen ein Spezialist für Statistik oder Informationstheorie ist - es sind diese beiden Arten von Spezialisten, die mit zufälligen Ereignissen vertraut sind. Ein Test hat gezeigt, dass ich recht hatte!

Dies ist eine traurige Folge Ihrer Ausbildung. Sie haben mit Liebe studiert, wie eine Theorie durch eine andere ersetzt wird, aber Sie haben nicht gelernt, wie man eine schöne Theorie aufgibt und den Zufall akzeptiert. Dies war genau das, was benötigt wurde: bereit zu sein, zuzugeben, dass die gerade gelesene Theorie nicht geeignet ist und es keine Regelmäßigkeit in den Daten gibt, reiner Zufall!

Ich muss näher darauf eingehen. Statistiker fragen sich ständig: "Was meine ich eigentlich, oder ist es nur zufälliges Rauschen?" Sie entwickelten spezielle Testmethoden, um diese Frage zu beantworten. Ihre Antworten sind kein definitives Ja oder Nein, sondern Ja oder Nein mit einem gewissen Maß an Vertrauen. Eine Konfidenzschwelle von 90% bedeutet, dass Sie sich bei 10 Versuchen normalerweise nur einmal irren, sofern alle anderen Hypothesen korrekt sind.In diesem Fall eines von zwei Dingen: Entweder haben Sie gefunden, was nicht ist (ein Fehler der ersten Art), oder Sie haben verpasst, wonach Sie gesucht haben (ein Fehler der zweiten Art). Es werden viel mehr Daten benötigt, um ein Konfidenzniveau von 95% zu erreichen, und die Datenerfassung kann derzeit sehr teuer sein. Das Sammeln zusätzlicher Daten erfordert auch zusätzliche Zeit und die Entscheidungsfindung wird verschoben - dies ist ein beliebter Trick von Personen, die nicht für ihre Entscheidungen verantwortlich sein möchten. "Benötigen Sie weitere Informationen", werden sie Ihnen sagen.

Ich bestätige absolut ernsthaft, dass die meisten durchgeführten Simulationen nichts anderes als ein Rorschach-Test sind. Ich zitiere einen herausragenden Praktiker der Kontrolltheorie von Jay Forrester: „Aus dem Verhalten des Systems ergeben sich Zweifel, die eine Überprüfung der ursprünglichen Annahmen erfordern. Durch die Verarbeitung der anfänglichen Annahmen über die Teile und das beobachtete Verhalten des Ganzen verbessern wir unser Verständnis der Struktur und Dynamik des Systems. Dieses Buch ist das Ergebnis mehrerer vom Autor abgeschlossener Wiederholungszyklen. “

Wie kann ein Laie dies vom Rorschach-Test unterscheiden? Hat er etwas gesehen, nur weil er es sehen wollte oder eine neue Facette der Realität entdeckt hat? Leider enthält die Modellierung sehr oft einige Anpassungen, mit denen Sie "nur das sehen können, was Sie wollen". Dies ist der Weg des geringsten Widerstands, weshalb die klassische Wissenschaft eine Vielzahl von Vorsichtsmaßnahmen beinhaltet, die in unserer Zeit oft einfach ignoriert werden.

Denken Sie, dass Sie vorsichtig genug sind, um nicht zu wünschen? Schauen wir uns die berühmte Doppelblindstudie an, die in der Medizin üblich ist. Zuerst stellten die Ärzte fest, dass die Patienten eine Verbesserung bemerkten, als sie dachten, sie würden ein neues Arzneimittel erhalten, während Patienten in der Kontrollgruppe, die wussten, dass sie kein neues Arzneimittel erhielten, keine Verbesserung verspürten. Danach randomisierten die Ärzte die Gruppen und begannen, einigen Patienten ein Placebo zu geben, damit sie die Ärzte nicht irreführen konnten. Zu ihrem Entsetzen stellten die Ärzte jedoch fest, dass die Ärzte, die wussten, wer das Arzneimittel einnahm und wer nicht, auch Verbesserungen bei denen fanden, die es erwartet hatten, und keine Verbesserung bei denen fanden, die es nicht erwartet hatten.Als letztes Mittel begannen die Ärzte, die doppelblinde Studienmethode allgemein anzuwenden - bis alle Daten gesammelt sind, wissen weder die Ärzte noch die Patienten, wer das neue Arzneimittel einnimmt und wer nicht. Am Ende des Experiments öffnen die Statistiker den versiegelten Umschlag und analysieren. Ärzte, die Ehrlichkeit suchten, stellten fest, dass sie es selbst nicht waren. Machst du die Simulation so viel besser, dass du vertrauenswürdig bist? Sind Sie sicher, dass Sie einfach nicht gefunden haben, wonach Sie so gesucht haben? Selbsttäuschung ist sehr verbreitet.Machst du die Simulation so viel besser, dass du vertrauenswürdig bist? Sind Sie sicher, dass Sie einfach nicht gefunden haben, wonach Sie so gesucht haben? Selbsttäuschung ist sehr verbreitet.Machst du die Simulation so viel besser, dass du vertrauenswürdig bist? Sind Sie sicher, dass Sie einfach nicht gefunden haben, wonach Sie so gesucht haben? Selbsttäuschung ist sehr verbreitet.

Ich begann Kapitel 19 mit der Frage, warum jeder glauben sollte, dass die Simulation durchgeführt wurde. Jetzt ist dieses Problem für Sie offensichtlicher geworden. Es ist nicht so einfach, diese Frage zu beantworten, bis Sie viel mehr Vorsichtsmaßnahmen treffen als normalerweise. Denken Sie auch daran, dass Sie in Ihrer High-Tech-Zukunft höchstwahrscheinlich die Kundenseite der Simulation repräsentieren und basierend auf den Ergebnissen Entscheidungen treffen müssen. Es gibt keine andere Möglichkeit als das Modellieren, um die Antwort auf die Frage "Was wäre wenn ...?" Zu erhalten. In Kapitel 18 habe ich über Entscheidungen nachgedacht, die getroffen werden sollten, und nicht die ganze Zeit aufgeschoben, wenn die Organisation nicht endlos stöbern und treiben möchte - ich gehe davon aus, dass Sie zu denen gehören, die eine Entscheidung treffen müssen.

Modellierung ist erforderlich, um die Frage „Was wäre wenn ...?“ Zu beantworten. Gleichzeitig ist sie jedoch voller Fallstricke, und Sie sollten ihren Ergebnissen nicht vertrauen, nur weil große Personal- und Hardwareressourcen verwendet wurden, um schöne Farbdrucke oder Kurven auf einem Oszilloskop zu erhalten. Wenn Sie derjenige sind, der die endgültige Entscheidung trifft, liegt alle Verantwortung bei Ihnen. Kollegiale Entscheidungen, die zu einer Verwischung der Verantwortung führen, sind selten eine gute Praxis - sie sind normalerweise ein mittelmäßiger Kompromiss, dem die Vorzüge eines der möglichen Wege fehlen. Die Erfahrung hat mich gelehrt, dass ein entscheidender Chef viel besser ist als ein plappernder Chef. In diesem Fall wissen Sie genau, wo Sie sich befinden, und können die zu erledigende Arbeit fortsetzen.

Die Frage "Was wäre wenn ...?" wird Sie in Zukunft häufig konfrontieren, daher müssen Sie sich mit den Grundlagen und Modellierungsfunktionen befassen, um bereit zu sein, die Ergebnisse herauszufordern und gegebenenfalls die Details zu verstehen.

Fortsetzung

folgt ... Wer bei der Übersetzung, dem Layout und der Veröffentlichung des Buches helfen möchte - schreiben Sie in eine persönliche E-Mail oder E-Mail magisterludi2016@yandex.ru

Übrigens haben wir auch die Übersetzung eines anderen coolen Buches veröffentlicht - "Die Traummaschine: Die Geschichte der Computerrevolution" )