Geekly articles weekly

Probabilistische Bitcoin-Mining-Methode



Ich denke, ein kleiner Unsinn am Dienstag wird der Arbeitswoche nicht schaden. Ich habe ein Hobby, in meiner Freizeit versuche ich herauszufinden, wie man den Bitcoin-Mining-Algorithmus hackt, dumme, unsinnige Suche vermeidet und eine Lösung für das Hash-Matching-Problem mit minimalem Energieverbrauch findet. Ich muss gleich sagen, das Ergebnis habe ich natürlich noch nicht erreicht, aber warum nicht die Ideen, die im Kopf geboren sind, schriftlich darlegen? Irgendwo müssen sie platziert werden ...

Trotz der Wahnvorstellungen der folgenden Ideen denke ich, dass dieser Artikel für jemanden nützlich sein kann, der studiert

  1. C ++ - Sprache und ihre Vorlagen
  2. einige digitale Schaltungen
  3. ein bisschen Wahrscheinlichkeitstheorie und probabilistische Arithmetik
  4. Bitcoin-Hashing-Algorithmus im Detail

Mit was fangen wir an?

Vielleicht vom letzten und langweiligsten Punkt auf dieser Liste? Geduld, dann wird es mehr Spaß machen.
Betrachten wir im Detail den Algorithmus zur Berechnung der Hashing-Funktion von Bitcoin. Es ist einfach F (x) = sha256 (sha256 (x)), wobei x die Eingabe von 80 Bytes, der Blockheader zusammen mit der Versionsnummer des Blocks, dem vorherigen Block-Hash, der Merkle-Wurzel, dem Zeitstempel, den Bits und Nonce ist. Hier sind Beispiele für relativ neue Blockheader, die an die Hashing-Funktion übergeben werden:

//blk=533522 0x00,0x00,0x00,0x20, 0x6d,0xa5,0xdd,0xb5,0x78,0x04,0x08,0x80,0xae,0x3d,0xed,0xc5,0x8e,0xe9,0x74,0x93,0x93,0x6d,0x6a,0xf4,0x0e,0x80,0x30,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00, 0xdf,0x3e,0xb0,0xf4,0x92,0xbf,0xe9,0xb8,0xc8,0x12,0x1f,0x84,0xdd,0x35,0xe1,0x38,0x09,0xcc,0x28,0xc2,0x33,0x53,0x90,0x4e,0x15,0x49,0x5e,0xc7,0xb0,0x78,0x35,0x91, 0x82,0xDB,0x57,0x5B, 0x17,0x5A,0x36,0x17, 0xAA,0x02,0x44,0x22, //blk=533523 0x00,0x00,0x00,0x20, 0x6a,0x27,0x37,0xc3,0x1f,0x68,0xf8,0xe3,0x03,0xa3,0x5d,0xff,0x2d,0x97,0x39,0xaf,0x81,0xa2,0xf5,0xf0,0x7c,0xdb,0x34,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00, 0xa1,0xb8,0x4f,0x75,0x66,0xf3,0xf3,0x8e,0x78,0xf7,0xa2,0xa2,0xa2,0x19,0xa1,0x18,0x45,0xfa,0x58,0x53,0xe4,0x05,0x50,0x12,0x57,0xa1,0xab,0x2c,0x39,0xe6,0x1f,0x63, 0xA0,0xDB,0x57,0x5B, 0x17,0x5A,0x36,0x17, 0x84,0x7B,0x86,0xE7, //blk=533524 0x00,0x00,0x00,0x20, 0xb3,0xc7,0xaa,0x07,0x26,0xdb,0xe8,0x58,0x19,0xa8,0xb9,0x53,0x08,0x62,0x8b,0xca,0x58,0x00,0x69,0x64,0x58,0x69,0x1a,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00, 0x4e,0xfc,0xf4,0x5c,0xad,0x31,0x44,0x5b,0xb1,0x13,0x80,0x03,0xe0,0xfd,0x04,0x24,0x86,0xcc,0x7a,0x8c,0xa7,0x7c,0x30,0x60,0x05,0x6f,0x43,0xcf,0x25,0x45,0x8f,0xd8, 0x80,0xDE,0x57,0x5B, 0x17,0x5A,0x36,0x17, 0xF7,0x2B,0x3B,0x42,

Dieser Satz von Bytes ist ein sehr wertvolles Material, da es für Bergleute oft nicht einfach ist, herauszufinden, in welcher Reihenfolge die Bytes beim Bilden des Headers folgen sollen, wobei häufig die Stellen von niedrigen und hohen Bytes (Endians) umgekehrt werden.

Aus dem Blockheader werden also 80 Bytes als sha256-Hash und dann aus dem Ergebnis ein weiterer sha256 betrachtet.
Der sha256-Algorithmus selbst besteht normalerweise aus vier Funktionen, wenn Sie verschiedene Quellen betrachten:

  1. void sha256_init (SHA256_CTX * ctx);
  2. void sha256_transform (SHA256_CTX * ctx, const BYTE data []);
  3. void sha256_update (SHA256_CTX * ctx, const BYTE-Daten [], size_t len);
  4. void sha256_final (SHA256_CTX * ctx, BYTE-Hash []);

Die erste Funktion, die bei der Berechnung des Hash aufgerufen wird, ist sha256_init (), wodurch die SHA256_CTX-Struktur wiederhergestellt wird. Es gibt dort nichts Besonderes außer acht 32-Bit-Statuswörtern, die anfänglich mit speziellen Wörtern gefüllt sind:

 void sha256_init(SHA256_CTX *ctx) { ctx->datalen = 0; ctx->bitlen = 0; ctx->state[0] = 0x6a09e667; ctx->state[1] = 0xbb67ae85; ctx->state[2] = 0x3c6ef372; ctx->state[3] = 0xa54ff53a; ctx->state[4] = 0x510e527f; ctx->state[5] = 0x9b05688c; ctx->state[6] = 0x1f83d9ab; ctx->state[7] = 0x5be0cd19; }

Angenommen, wir haben eine Datei, deren Hash berechnet werden muss. Wir lesen die Datei mit Blöcken beliebiger Größe und rufen die Funktion sha256_update () auf, bei der wir den Zeiger auf die Blockdaten und die Blocklänge übergeben. Die Funktion akkumuliert den Hash in der Struktur SHA256_CTX im Statusarray:

 void sha256_update(SHA256_CTX *ctx, const BYTE data[], size_t len) { uint32_t i; for (i = 0; i < len; ++i) { ctx->data[ctx->datalen] = data[i]; ctx->datalen++; if (ctx->datalen == 64) { sha256_transform(ctx, ctx->data); ctx->bitlen += 512; ctx->datalen = 0; } } }

Sha256_update () ruft an sich die Arbeitspferdfunktion sha256_transform () auf, die bereits Blöcke mit nur einer festen Länge von 64 Bytes akzeptiert:

 /****************************** MACROS ******************************/ #define ROTLEFT(a,b) (((a) << (b)) | ((a) >> (32-(b)))) #define ROTRIGHT(a,b) (((a) >> (b)) | ((a) << (32-(b)))) #define CH(x,y,z) (((x) & (y)) ^ (~(x) & (z))) #define MAJ(x,y,z) (((x) & (y)) ^ ((x) & (z)) ^ ((y) & (z))) #define EP0(x) (ROTRIGHT(x,2) ^ ROTRIGHT(x,13) ^ ROTRIGHT(x,22)) #define EP1(x) (ROTRIGHT(x,6) ^ ROTRIGHT(x,11) ^ ROTRIGHT(x,25)) #define SIG0(x) (ROTRIGHT(x,7) ^ ROTRIGHT(x,18) ^ ((x) >> 3)) #define SIG1(x) (ROTRIGHT(x,17) ^ ROTRIGHT(x,19) ^ ((x) >> 10)) /**************************** VARIABLES *****************************/ static const uint32_t k[64] = { 0x428a2f98,0x71374491,0xb5c0fbcf,0xe9b5dba5,0x3956c25b,0x59f111f1,0x923f82a4,0xab1c5ed5, 0xd807aa98,0x12835b01,0x243185be,0x550c7dc3,0x72be5d74,0x80deb1fe,0x9bdc06a7,0xc19bf174, 0xe49b69c1,0xefbe4786,0x0fc19dc6,0x240ca1cc,0x2de92c6f,0x4a7484aa,0x5cb0a9dc,0x76f988da, 0x983e5152,0xa831c66d,0xb00327c8,0xbf597fc7,0xc6e00bf3,0xd5a79147,0x06ca6351,0x14292967, 0x27b70a85,0x2e1b2138,0x4d2c6dfc,0x53380d13,0x650a7354,0x766a0abb,0x81c2c92e,0x92722c85, 0xa2bfe8a1,0xa81a664b,0xc24b8b70,0xc76c51a3,0xd192e819,0xd6990624,0xf40e3585,0x106aa070, 0x19a4c116,0x1e376c08,0x2748774c,0x34b0bcb5,0x391c0cb3,0x4ed8aa4a,0x5b9cca4f,0x682e6ff3, 0x748f82ee,0x78a5636f,0x84c87814,0x8cc70208,0x90befffa,0xa4506ceb,0xbef9a3f7,0xc67178f2 }; /*********************** FUNCTION DEFINITIONS ***********************/ void sha256_transform(SHA256_CTX *ctx, const BYTE data[]) { uint32_t a, b, c, d, e, f, g, h, i, j, t1, t2, m[64]; for (i = 0, j = 0; i < 16; ++i, j += 4) m[i] = (data[j] << 24) | (data[j + 1] << 16) | (data[j + 2] << 8) | (data[j + 3]); for (; i < 64; ++i) m[i] = SIG1(m[i - 2]) + m[i - 7] + SIG0(m[i - 15]) + m[i - 16]; a = ctx->state[0]; b = ctx->state[1]; c = ctx->state[2]; d = ctx->state[3]; e = ctx->state[4]; f = ctx->state[5]; g = ctx->state[6]; h = ctx->state[7]; for (i = 0; i < 64; ++i) { t1 = h + EP1(e) + CH(e, f, g) + k[i] + m[i]; t2 = EP0(a) + MAJ(a, b, c); h = g; g = f; f = e; e = d + t1; d = c; c = b; b = a; a = t1 + t2; } ctx->state[0] += a; ctx->state[1] += b; ctx->state[2] += c; ctx->state[3] += d; ctx->state[4] += e; ctx->state[5] += f; ctx->state[6] += g; ctx->state[7] += h; }

Wenn die gesamte Hash-Datei gelesen und bereits in die Funktion sha256_update () übertragen wurde, muss nur noch die endgültige Funktion sha256_final () aufgerufen werden. Wenn die Dateigröße nicht ein Vielfaches von 64 Bytes beträgt, werden zusätzliche Füllbytes hinzugefügt, die Gesamtdatenlänge am Ende des letzten Datenblocks geschrieben und wird die endgültige sha256_transform () ausführen.
Das Hash-Ergebnis bleibt im Statusarray.

Dies ist sozusagen das „hohe Niveau“.

In Bezug auf den Bitcoin-Miner denken die Entwickler natürlich darüber nach, wie sie kleiner und effizienter denken können.

Es ist ganz einfach: Der Header enthält nur 80 Bytes, was kein Vielfaches von 64 Bytes ist. Daher müsste der erste sha256 bereits zwei sha256_transform () ausführen. Zum Glück für Bergleute befindet sich das Nonce des Blocks jedoch am Ende des Headers, sodass die erste sha256_transform () nur einmal ausgeführt werden kann - dies ist der sogenannte Midstate. Als nächstes geht der Miner alle unsinnigen Optionen durch, die 4 Milliarden, 2 ^ 32 sind, und ersetzt sie im entsprechenden Feld durch die zweite sha256_transform (). Diese Transformation vervollständigt die erste sha256-Funktion. Das Ergebnis sind acht 32-Bit-Wörter, dh 32 Bytes. Es ist einfach, sha256 von ihnen zu finden - die endgültige sha256_transform () wird aufgerufen und alles ist fertig. Beachten Sie, dass die Eingabedaten 32 Byte kleiner sind als die 64 Bytes, die für sha256_transform () benötigt werden. Also wird der Block wieder mit Nullen aufgefüllt und die Blocklänge wird am Ende eingegeben.

Insgesamt gibt es nur drei Aufrufe von sha256_transform (), von denen der erste nur einmal gelesen werden muss, um den mittleren Zustand zu berechnen.

Ich habe versucht, alle Datenmanipulationen, die beim Berechnen des Hashs des Headers eines Bitcoin-Blocks auftreten, auf eine einzige Funktion zu erweitern, damit klar ist, wie die gesamte Berechnung speziell für Bitcoin abläuft, und Folgendes ist passiert:

 //get bitcoin header via ptr to 80 bytes and calc hash template <typename T> void full_btc_hash(const uint8_t* ptr80, T nonce, T* presult) { //-1------------------------------------------ //init sha256 state s[7:0] T s[16]; for (int i = 0; i < 8; i++) { s[i] = sha256_init_state[i]; presult[i] = sha256_init_state[i]; } uint8_t tail2[] = { 0x80,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00, 0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x01,0x00, }; uint32_t* p = (uint32_t*)tail2; for (int i = 0; i < 8; i++) { s[i + 8] = ntohl(p[i]); } //get first block for sha256 uint8_t tail[] = { /* 2nd sha256 block padding */ 0x80,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00, 0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00, 0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x02,0x80 }; T blk1[32]; p = (uint32_t*)ptr80; for (int i = 0; i < 19; i++) { blk1[i] = ntohl(p[i]); } //put nonce here blk1[19] = nonce; p = (uint32_t*)tail; for (int i = 0; i < 12; i++) { blk1[i + 20] = ntohl(p[i]); } sha256_transform(s, &blk1[0]); //warning! this can be called only once and produce MIDSTATE sha256_transform(s, &blk1[16]); sha256_transform(presult, s); }

Ich habe diese Funktion als C ++ - Vorlage implementiert. Sie kann nicht nur 32-Bit-Wörter verarbeiten, z. B. uint32_t, sondern auch Wörter eines anderen Typs „T“ auf dieselbe Weise. Ich habe hier und der Zustand sha256 wird als Array vom Typ "T" gespeichert und sha256_transform () wird mit einem Parameterzeiger auf ein Array vom Typ "T" aufgerufen und das Ergebnis wird gleich zurückgegeben. Die Transformationsfunktion hat jetzt auch die Form einer C ++ - Vorlage:

 template <typename T> T ror32(T word, unsigned int shift) { return (word >> shift) | (word << (32 - shift)); } template <typename T> T Ch(T x, T y, T z) { return z ^ (x & (y ^ z)); } template<typename T> T Maj(T x, T y, T z) { return (x & y) | (z & (x | y)); } #define e0(x) (ror32(x, 2) ^ ror32(x,13) ^ ror32(x,22)) #define e1(x) (ror32(x, 6) ^ ror32(x,11) ^ ror32(x,25)) #define s0(x) (ror32(x, 7) ^ ror32(x,18) ^ (x >> 3)) #define s1(x) (ror32(x,17) ^ ror32(x,19) ^ (x >> 10)) unsigned int ntohl(unsigned int in) { return ((in & 0xff) << 24) | ((in & 0xff00) << 8) | ((in & 0xff0000) >> 8) | ((in & 0xff000000) >> 24); } template <typename T> void LOAD_OP(int I, T *W, const u8 *input) { //W[I] = /*ntohl*/ (((u32*)(input))[I]); W[I] = ntohl(((u32*)(input))[I]); //W[I] = (input[3] << 24) | (input[2] << 16) | (input[1] << 8) | (input[0]); } template <typename T> void BLEND_OP(int I, T *W) { W[I] = s1(W[I - 2]) + W[I - 7] + s0(W[I - 15]) + W[I - 16]; } template <typename T> void sha256_transform(T *state, const T *input) { T a, b, c, d, e, f, g, h, t1, t2; TW[64]; int i; /* load the input */ for (i = 0; i < 16; i++) // MJ input is cast to u32* so this processes 16 DWORDS = 64 bytes W[i] = input[i]; /* now blend */ for (i = 16; i < 64; i++) BLEND_OP(i, W); /* load the state into our registers */ a = state[0]; b = state[1]; c = state[2]; d = state[3]; e = state[4]; f = state[5]; g = state[6]; h = state[7]; // t1 = h + e1(e) + Ch(e, f, g) + 0x428a2f98 + W[0]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0x71374491 + W[1]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0xb5c0fbcf + W[2]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0xe9b5dba5 + W[3]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0x3956c25b + W[4]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0x59f111f1 + W[5]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0x923f82a4 + W[6]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0xab1c5ed5 + W[7]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; t1 = h + e1(e) + Ch(e, f, g) + 0xd807aa98 + W[8]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0x12835b01 + W[9]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0x243185be + W[10]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0x550c7dc3 + W[11]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0x72be5d74 + W[12]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0x80deb1fe + W[13]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0x9bdc06a7 + W[14]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0xc19bf174 + W[15]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; t1 = h + e1(e) + Ch(e, f, g) + 0xe49b69c1 + W[16]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0xefbe4786 + W[17]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0x0fc19dc6 + W[18]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0x240ca1cc + W[19]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0x2de92c6f + W[20]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0x4a7484aa + W[21]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0x5cb0a9dc + W[22]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0x76f988da + W[23]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; t1 = h + e1(e) + Ch(e, f, g) + 0x983e5152 + W[24]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0xa831c66d + W[25]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0xb00327c8 + W[26]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0xbf597fc7 + W[27]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0xc6e00bf3 + W[28]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0xd5a79147 + W[29]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0x06ca6351 + W[30]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0x14292967 + W[31]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; t1 = h + e1(e) + Ch(e, f, g) + 0x27b70a85 + W[32]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0x2e1b2138 + W[33]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0x4d2c6dfc + W[34]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0x53380d13 + W[35]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0x650a7354 + W[36]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0x766a0abb + W[37]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0x81c2c92e + W[38]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0x92722c85 + W[39]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; t1 = h + e1(e) + Ch(e, f, g) + 0xa2bfe8a1 + W[40]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0xa81a664b + W[41]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0xc24b8b70 + W[42]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0xc76c51a3 + W[43]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0xd192e819 + W[44]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0xd6990624 + W[45]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0xf40e3585 + W[46]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0x106aa070 + W[47]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; t1 = h + e1(e) + Ch(e, f, g) + 0x19a4c116 + W[48]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0x1e376c08 + W[49]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0x2748774c + W[50]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0x34b0bcb5 + W[51]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0x391c0cb3 + W[52]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0x4ed8aa4a + W[53]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0x5b9cca4f + W[54]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0x682e6ff3 + W[55]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; t1 = h + e1(e) + Ch(e, f, g) + 0x748f82ee + W[56]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0x78a5636f + W[57]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0x84c87814 + W[58]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0x8cc70208 + W[59]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0x90befffa + W[60]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0xa4506ceb + W[61]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0xbef9a3f7 + W[62]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0xc67178f2 + W[63]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; state[0] += a; state[1] += b; state[2] += c; state[3] += d; state[4] += e; state[5] += f; state[6] += g; state[7] += h; }

Die Verwendung von C ++ - Vorlagenfunktionen ist praktisch, da ich den benötigten Hash aus regulären Daten berechnen und das übliche Ergebnis erhalten kann:

  const uint8_t header[] = { 0x02,0x00,0x00,0x00, 0x17,0x97,0x5b,0x97,0xc1,0x8e,0xd1,0xf7, 0xe2,0x55,0xad,0xf2,0x97,0x59,0x9b,0x55, 0x33,0x0e,0xda,0xb8,0x78,0x03,0xc8,0x17, 0x01,0x00,0x00,0x00,0x00,0x00,0x00,0x00, 0x8a,0x97,0x29,0x5a,0x27,0x47,0xb4,0xf1, 0xa0,0xb3,0x94,0x8d,0xf3,0x99,0x03,0x44, 0xc0,0xe1,0x9f,0xa6,0xb2,0xb9,0x2b,0x3a, 0x19,0xc8,0xe6,0xba, 0xdc,0x14,0x17,0x87, 0x35,0x8b,0x05,0x53, 0x53,0x5f,0x01,0x19, 0x48,0x75,0x08,0x33 }; uint32_t test_nonce = 0x48750833; uint32_t result[8]; full_btc_hash(header, test_nonce, result); uint8_t* presult = (uint8_t * )result; for (int i = 0; i < 32; i++) printf("%02X ", presult[i]);

Es stellt sich heraus:

92 98 2A 50 91 FA BD 42 97 8A A5 2D CD C9 36 28 02 4A DD FE E0 67 A4 78 00 00 00 00 00 00 00

Am Ende des Hash gibt es viele Nullen, einen schönen Hash, Bingo usw.

Und jetzt kann ich nicht gewöhnliche uint32_t-Daten an diese Hashing-Funktion übergeben, sondern meine spezielle C ++ - Klasse, die alle Arithmetik neu definiert.

Ja Ja. Ich werde "alternative" probabilistische Mathematik anwenden.
Ich habe es selbst erfunden, realisiert, selbst erlebt. Es scheint nicht sehr gut zu funktionieren. Ein Witz. Es sollte funktionieren. Vielleicht bin ich nicht der erste, den ich ankurbeln möchte.

Nun kommen wir zu den interessantesten.
Alle Arithmetik in der digitalen Elektronik wird als Operationen an Bits ausgeführt und ist streng durch die Operationen AND, OR, NOT, EXCLUSIVE OR definiert. Nun, wir alle wissen, was Wahrheitstabellen in der Booleschen Algebra sind.

Ich schlage vor, den Berechnungen ein wenig Unsicherheit hinzuzufügen, um sie probabilistisch zu machen.
Lassen Sie jedes Bit im Wort nicht nur die möglichen ZERO- und ONE-Werte haben, sondern auch alle Zwischenwerte! Ich schlage vor, den Wert eines Bits als die Wahrscheinlichkeit eines Ereignisses zu betrachten, das auftreten kann oder nicht. Wenn alle Anfangsdaten zuverlässig bekannt sind, ist das Ergebnis zuverlässig. Und wenn einige Daten etwas fehlen, wird sich das Ergebnis mit einiger Wahrscheinlichkeit herausstellen.

Angenommen, es gibt zwei unabhängige Ereignisse "a" und "b", deren Eintrittswahrscheinlichkeit natürlich von null bis eins ist, Pa und Pb. Wie hoch ist die Wahrscheinlichkeit, dass Ereignisse gleichzeitig eintreten? Ich bin sicher, dass jeder von uns nicht zögern wird, P = Pa * Pb zu beantworten, und dies ist die richtige Antwort!

Das 3D-Diagramm einer solchen Funktion sieht folgendermaßen aus (aus zwei verschiedenen Blickwinkeln):



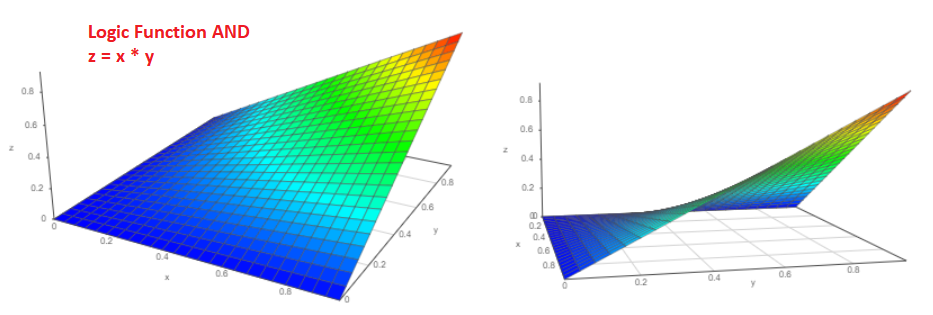
Und wie hoch ist die Wahrscheinlichkeit, dass entweder das Pa-Ereignis oder das Pb-Ereignis eintreten wird?
Wahrscheinlichkeit P = Pa + Pb-Pa * Pb. Das Funktionsdiagramm sieht folgendermaßen aus:



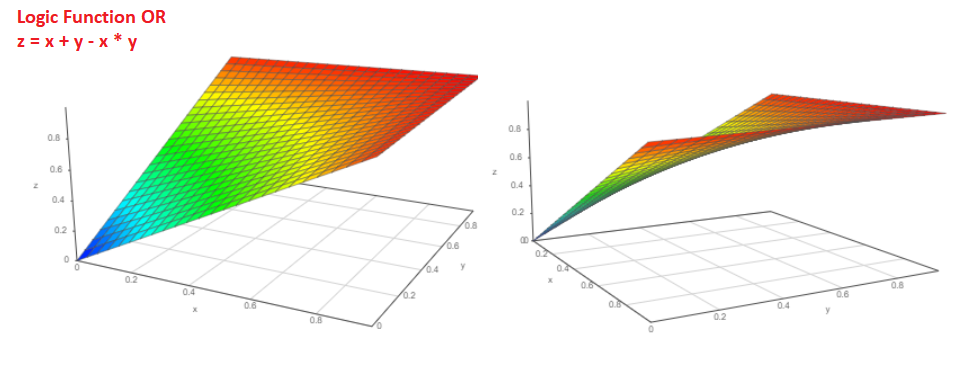
Und wenn wir die Wahrscheinlichkeit des Eintretens des Ereignisses Pa kennen, wie groß ist dann die Wahrscheinlichkeit, dass das Ereignis nicht eintreten wird?
P = 1 - Pa.

Nehmen wir nun eine Annahme an. Stellen Sie sich vor, wir haben logische Elemente, die die Wahrscheinlichkeit eines Ausgabeereignisses berechnen und die Wahrscheinlichkeit von Eingabeereignissen kennen:



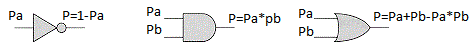
Solche logischen Elemente können sie leicht komplexer machen, z. B. exklusiv oder XOR:



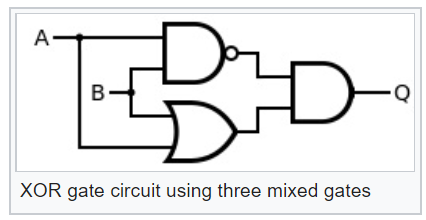
Wenn wir uns nun das Diagramm dieses XOR-Logikelements ansehen, können wir verstehen, wie hoch die Wahrscheinlichkeit des Ereignisses am Ausgang des probabilistischen XOR sein wird:



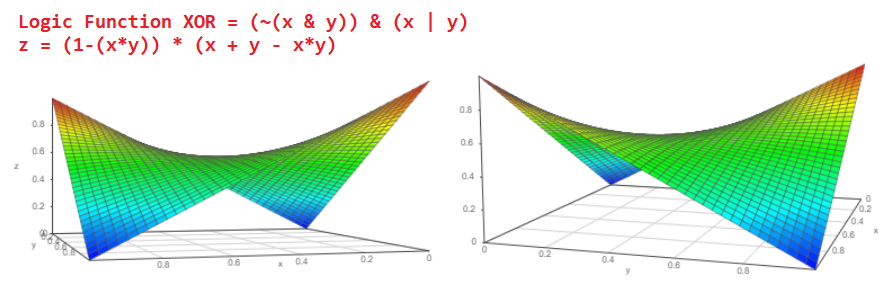
Das ist aber noch nicht alles. Wir kennen die typische Logik eines Volladdierers und finden heraus, wie ein Mehrbitaddierer aus einem Volladdierer hergestellt wird:



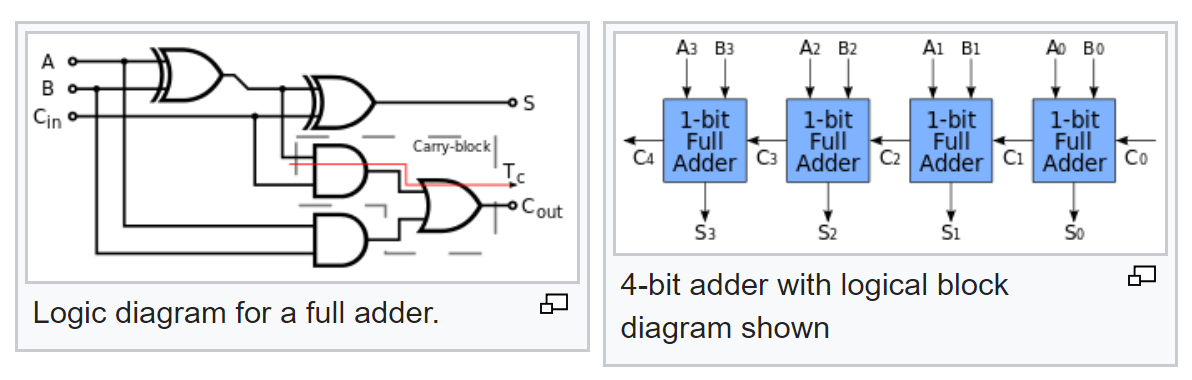
Nach seinem Schema können wir nun die Wahrscheinlichkeiten von Signalen am Ausgang mit bekannten Wahrscheinlichkeiten von Signalen am Eingang berechnen.

Somit kann ich in c ++ meine eigene 32-Bit-Klasse (ich werde sie x32 nennen) mit probabilistischer Arithmetik implementieren und diese Klasse für alle sha256-Operationen wie AND, OR, XOR, ADD und Shifts überschreiben. Die Klasse speichert 32 Bits im Inneren, aber jedes Bit ist eine Gleitkommazahl. Jede logische oder arithmetische Operation mit einer solchen 32-Bit-Zahl berechnet die Wahrscheinlichkeit des Wertes jedes Bits mit bekannten oder wenig bekannten Eingabeparametern einer logischen oder arithmetischen Operation.

Betrachten Sie ein sehr einfaches Beispiel, das meine probabilistische Mathematik verwendet:

 typedef std::numeric_limits< double > dbl; int main(int argc, char *argv[]) { cout.precision(dbl::max_digits10); x32 a = 0xaabbccdd; x32 b = 0x12345678; <b>//b.setBit( 4, 0.75 );</b> x32 c = a + b; cout << std::hex << "result = 0x" << c.get32() << "\n" << std::dec; for (int i = 0; i < 32; i++) cout << "bit" << i << " = " << c.get_bvi(i) << "\n"; cout << "ok\n"; }

In diesem Beispiel werden zwei 32-Bit-Zahlen hinzugefügt.
Während der String b.setBit (4, 0.75) ist; Das Ergebnis der Addition wird genau vorhersehbar und vorbestimmt auskommentiert, da alle Eingabedaten für die Addition bekannt sind. Das Programm druckt dies auf die Konsole:

 result = 0xbcf02355 bit0 = 1 bit1 = 0 bit2 = 1 bit3 = 0 bit4 = 1 bit5 = 0 bit6 = 1 bit7 = 0 bit8 = 1 bit9 = 1 bit10 = 0 bit11 = 0 bit12 = 0 bit13 = 1 bit14 = 0 bit15 = 0 bit16 = 0 bit17 = 0 bit18 = 0 bit19 = 0 bit20 = 1 bit21 = 1 bit22 = 1 bit23 = 1 bit24 = 0 bit25 = 0 bit26 = 1 bit27 = 1 bit28 = 1 bit29 = 1 bit30 = 0 bit31 = 1

Wenn ich die Zeile b.setBit (4, 0.75) auskommentiere, würde ich dem Programm damit sagen: "Addiere diese beiden Zahlen zu mir, aber ich kenne den Wert von Bit 4 des zweiten Arguments nicht wirklich, ich denke, es ist einer mit einer Wahrscheinlichkeit von 0,75."

Dann erfolgt die Addition, wie es sein sollte, mit einer vollständigen Berechnung der Wahrscheinlichkeiten der Ausgangssignale, d. H. Bits:

 bit not stable bit not stable bit not stable result = 0xbcf02305 bit0 = 1 bit1 = 0 bit2 = 1 bit3 = 0 bit4 = 0.75 bit5 = 0.1875 bit6 = 0.8125 bit7 = 0 bit8 = 1 bit9 = 1 bit10 = 0 bit11 = 0 bit12 = 0 bit13 = 1 bit14 = 0 bit15 = 0 bit16 = 0 bit17 = 0 bit18 = 0 bit19 = 0 bit20 = 1 bit21 = 1 bit22 = 1 bit23 = 1 bit24 = 0 bit25 = 0 bit26 = 1 bit27 = 1 bit28 = 1 bit29 = 1 bit30 = 0 bit31 = 1

Aufgrund der Tatsache, dass die Eingabedaten nicht sehr bekannt waren, ist das Ergebnis nicht sehr bekannt. Darüber hinaus gilt das, was zuverlässig berechnet werden kann, als zuverlässig. Was nicht gezählt werden kann, wird mit Wahrscheinlichkeit betrachtet.

Jetzt, da ich eine so wunderbare 32-Bit-C ++ - Klasse für Fuzzy-Arithmetik habe, kann ich Arrays von Variablen vom Typ x32 an die Funktion full_btc_hash () in der Vorlage übergeben und ein wahrscheinlich geschätztes Hash-Ergebnis erhalten.

Einige der Implementierungen der x32-Klasse sind:
 #pragma once #include <string> #include <list> #include <iostream> #include <utility> #include <stdint.h> #include <vector> #include <limits> using namespace std; #include <boost/math/constants/constants.hpp> #include <boost/multiprecision/cpp_dec_float.hpp> using boost::multiprecision::cpp_dec_float_50; //typedef double MY_FP; typedef cpp_dec_float_50 MY_FP; class x32 { public: x32(); x32(uint32_t n); void init(MY_FP val); void init(double* pval); void setBit(int i, MY_FP val) { bvi[i] = val; }; ~x32() {}; x32 operator|(const x32& right); x32 operator&(const x32& right); x32 operator^(const x32& right); x32 operator+(const x32& right); x32& x32::operator+=(const x32& right); x32 operator~(); x32 operator<<(const unsigned int& right); x32 operator>>(const unsigned int& right); void print(); uint32_t get32(); MY_FP get_bvi(uint32_t idx) { return bvi[idx]; }; private: MY_FP not(MY_FP a); MY_FP and(MY_FP a, MY_FP b); MY_FP or (MY_FP a, MY_FP b); MY_FP xor(MY_FP a, MY_FP b); MY_FP bvi[32]; //bit values }; #include "stdafx.h" #include "x32.h" x32::x32() { for (int i = 0; i < 32; i++) { bvi[i] = 0.0; } } x32::x32(uint32_t n) { for (int i = 0; i < 32; i++) { bvi[i] = (n&(1 << i)) ? 1.0 : 0.0; } } void x32::init(MY_FP val) { for (int i = 0; i < 32; i++) { bvi[i] = val; } } void x32::init(double* pval) { for (int i = 0; i < 32; i++) { bvi[i] = pval[i]; } } x32 x32::operator<<(const unsigned int& right) { x32 t; for (int i = 31; i >= 0; i--) { if (i < right) { t.bvi[i] = 0.0; } else { t.bvi[i] = bvi[i - right]; } } return t; } x32 x32::operator>>(const unsigned int& right) { x32 t; for (unsigned int i = 0; i < 32; i++) { if (i >= (32 - right)) { t.bvi[i] = 0; } else { t.bvi[i] = bvi[i + right]; } } return t; } MY_FP x32::not(MY_FP a) { return 1.0 - a; } MY_FP x32::and(MY_FP a, MY_FP b) { return a * b; } MY_FP x32::or(MY_FP a, MY_FP b) { return a + b - a * b; } MY_FP x32::xor (MY_FP a, MY_FP b) { //(~(A & B)) & (A | B) return and( not( and(a,b) ) , or(a,b) ); } x32 x32::operator|(const x32& right) { x32 t; for (int i = 0; i < 32; i++) { t.bvi[i] = or ( bvi[i], right.bvi[i] ); } return t; } x32 x32::operator&(const x32& right) { x32 t; for (int i = 0; i < 32; i++) { t.bvi[i] = and (bvi[i], right.bvi[i]); } return t; } x32 x32::operator~() { x32 t; for (int i = 0; i < 32; i++) { t.bvi[i] = not(bvi[i]); } return t; } x32 x32::operator^(const x32& right) { x32 t; for (int i = 0; i < 32; i++) { t.bvi[i] = xor (bvi[i], right.bvi[i]); } return t; } x32 x32::operator+(const x32& right) { x32 r; r.bvi[0] = xor (bvi[0], right.bvi[0]); MY_FP cout = and (bvi[0], right.bvi[0]); for (unsigned int i = 1; i < 32; i++) { MY_FP xor_a_b = xor (bvi[i], right.bvi[i]); r.bvi[i] = xor( xor_a_b, cout ); MY_FP and1 = and (bvi[i], right.bvi[i]); MY_FP and2 = and (xor_a_b, cout); cout = or (and1,and2); } return r; } x32& x32::operator+=(const x32& right) { MY_FP cout = and (bvi[0], right.bvi[0]); bvi[0] = xor (bvi[0], right.bvi[0]); for (unsigned int i = 1; i < 32; i++) { MY_FP xor_a_b = xor (bvi[i], right.bvi[i]); MY_FP and1 = and (bvi[i], right.bvi[i]); MY_FP and2 = and (xor_a_b, cout); bvi[i] = xor (xor_a_b, cout); cout = or (and1, and2); } return *this; } void x32::print() { for (int i = 0; i < 32; i++) { cout << bvi[i] << "\n"; } } uint32_t x32::get32() { uint32_t r = 0; for (int i = 0; i < 32; i++) { if (bvi[i] == 1.0) r = r | (1 << i); else if (bvi[i] == 0.0) { //ok } else { //oops.. cout << "bit not stable\n"; } } return r; }


Wofür ist das alles?

Bitcoin Miner weiß nicht im Voraus, welchen Wert 32x Nonce auswählen soll. Der Bergmann ist gezwungen, über alle 4 Milliarden von ihnen zu iterieren, um den Hash zu zählen, bis er „schön“ wird, bis der Hash-Wert unter dem Ziel liegt.

Mit der Fuzzy-Wahrscheinlichkeitsarithmetik können Sie theoretisch die Sortierung aufheben.

Ja, ich kenne zunächst nicht die Bedeutung aller erforderlichen unsse Bits. Wenn ich sie nicht kenne, lass es keine Scheiße geben - die anfängliche Wahrscheinlichkeit von Nicht-Bits beträgt 0,5. Selbst in diesem Szenario kann ich die Wahrscheinlichkeit der Ausgabe von Hash-Bits berechnen. Irgendwo etwas, das sich auch als ungefähr 0,5 plus oder minus einen halben Penny herausstellt.

Jetzt kann ich jedoch nur ein unsse Bit von 0,5 auf 0,9 oder auf 0,1 oder auf 1,0 ändern und sehen, wie sich der Wahrscheinlichkeitswert des Signalwerts jedes Bits der Hash-Funktion am Ausgang ändert. Jetzt habe ich viel mehr Bewertungsinformationen. Ich kann jetzt jedes unsinnige Eingangsbit einzeln fühlen und sehen, wo sich die Wahrscheinlichkeit des Signals auf jedem der Ausgangsbits der Hash-Funktion verschiebt.

Hier ist zum Beispiel ein Fragment, das eine Hash-Funktion mit völlig unbekannten Nicht-Bits berücksichtigt, wenn die Wahrscheinlichkeit ihres Bitwerts 0,5 beträgt, und die zweite Berechnung, wenn wir annehmen, dass der Wert des Nonce-Bits [0] = 0,9 ist:

 typedef std::numeric_limits< double > dbl; int main(int argc, char *argv[]) { cout.precision(dbl::max_digits10); //--------------------------------- //hash: 502A989242BDFA912DA58A972836C9CDFEDD4A0278A467E00000000000000000 const u8 strxx[] = { 0x02,0x00,0x00,0x00, 0x17,0x97,0x5b,0x97,0xc1,0x8e,0xd1,0xf7, 0xe2,0x55,0xad,0xf2,0x97,0x59,0x9b,0x55, 0x33,0x0e,0xda,0xb8,0x78,0x03,0xc8,0x17, 0x01,0x00,0x00,0x00,0x00,0x00,0x00,0x00, 0x8a,0x97,0x29,0x5a,0x27,0x47,0xb4,0xf1, 0xa0,0xb3,0x94,0x8d,0xf3,0x99,0x03,0x44, 0xc0,0xe1,0x9f,0xa6,0xb2,0xb9,0x2b,0x3a, 0x19,0xc8,0xe6,0xba, 0xdc,0x14,0x17,0x87, 0x35,0x8b,0x05,0x53, 0x53,0x5f,0x01,0x19, 0x48,0x75,0x08,0x33 }; double nonce_bits[32]; for (int i = 0; i < 32; i++) nonce_bits[i] = 0.5; x32 nonce_x32_a; x32 nonce_x32_b; nonce_x32_a.init(nonce_bits); nonce_bits[0] = 0.9; nonce_x32_b.init(nonce_bits); x32 result_x32_a[8]; x32 result_x32_b[8]; full_btc_hash(strxx, nonce_x32_a, result_x32_a); full_btc_hash(strxx, nonce_x32_b, result_x32_b); for (int i = 0; i < 32; i++) cout << result_x32_a[7].get_bvi(i) << " " << result_x32_b[7].get_bvi(i) << "\n";

Die Klassenfunktion x32 :: get_bvi () gibt die Wahrscheinlichkeit des Bitwerts dieser Zahl zurück.
Wir berechnen und sehen, dass, wenn Sie den Wert des Nonce [0] -Bits von 0,5 auf 0,9 ändern, einige Bits des Ausgabe-Hashs kaum nach oben und andere kaum nach unten schwanken:

 0.44525679540883948 0.44525679540840074 0.55268174813167364 0.5526817481315932 0.57758654725359399 0.57758654725360606 0.49595026978928474 0.49595026978930477 0.57118578561406703 0.57118578561407746 0.53237003739057907 0.5323700373905661 0.57269859374138096 0.57269859374138162 0.57631236396381141 0.5763123639638157 0.47943176373960149 0.47943176373960219 0.54955992675177704 0.5495599267517755 0.53321116270879686 0.53321116270879733 0.57294025883744952 0.57294025883744984 0.53131857821387693 0.53131857821387655 0.57253530821899101 0.57253530821899102 0.50661432403287194 0.50661432403287198 0.57149419848354913 0.57149419848354916 0.53220327148366491 0.53220327148366487 0.57268927270412251 0.57268927270412251 0.57632130426913003 0.57632130426913005 0.57233970084776142 0.57233970084776143 0.56824728628552812 0.56824728628552813 0.45247155441889921 0.45247155441889922 0.56875940568326509 0.56875940568326509 0.57524323439326321 0.57524323439326321 0.57587726902392535 0.57587726902392535 0.57597043124557292 0.57597043124557292 0.52847748894672118 0.52847748894672118 0.54512141953055808 0.54512141953055808 0.57362254577539695 0.57362254577539695 0.53082194129771177 0.53082194129771177 0.54404489702929382 0.54404489702929382 0.54065386336136847 0.54065386336136847

Eine Art Atemzug, eine kaum wahrnehmbare Veränderung der Wahrscheinlichkeit eines Austritts 10 m nach dem Komma. Nun, trotzdem ... können Sie versuchen, einige Annahmen darauf aufzubauen. Es fällt wunderschön aus, oder?

Übrigens, wenn die Eingangsbits des Eingangs-Nonse mit den richtigen, notwendigen Wahrscheinlichkeitswerten wie folgt initialisiert werden:

 double nonce_bits[32]; for (int i = 0; i < 32; i++) nonce_bits[i] = (real_nonce32&(1 << i)) ? 1.0 : 0.0; x32 nonce_x32; nonce_x32.init(nonce_bits); full_btc_hash(strxx, nonce_x32, result_x32);

Wenn wir dann den probabilistischen Hash berechnen, erhalten wir das logisch korrekte Ergebnis - einen „schönen“ Hash am Ausgang, Bingo.

Mit Mathe stimmt hier also alles.

Es bleibt zu lernen, wie man den Atem der Brise analysiert ... und der Hasch ist gebrochen.
Es klingt nach Unsinn, aber das ist Unsinn - und ich habe ganz am Anfang gewarnt.

Andere nützliche Materialien:

  1. Minimieren Sie Bitcoin mit Papier und Stift.
  2. Ist es möglich, Bitcoins schneller, einfacher oder einfacher zu berechnen?
  3. Wie habe ich Blakecoin Miner gemacht?
  4. FPGA Bitcoin Miner auf Mars Rover Board 3
  5. FPGA Miner mit Blake-Algorithmus

Source: https://habr.com/ru/post/de420131/

More articles:


All Articles