FPGA Integer FFT-Implementierung

Hallo allerseits!

Einmal fragten mich Kunden, ob ich in meinen Projekten eine ganzzahlige FFT habe, worauf ich immer antwortete, dass dies bereits von anderen in Form von vorgefertigten, wenn auch gekrümmten, aber freien IP-Kernen (Altera / Xilinx) durchgeführt wurde - nehmen Sie es und verwenden Sie es. Diese Kerne sind jedoch nicht optimal , weisen eine Reihe von „Merkmalen“ auf und müssen weiter verfeinert werden. In diesem Zusammenhang begann ich nach einem weiteren geplanten Urlaub, den ich nicht mittelmäßig verbringen wollte, mit der Implementierung des konfigurierbaren Kernels der ganzzahligen FFT.


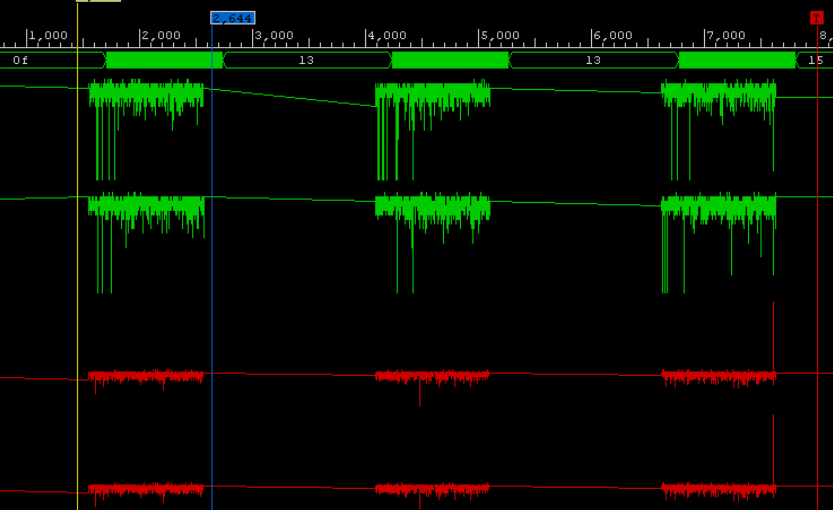_{KDPV (Prozess zum Debuggen von Datenüberlauffehlern)}

In dem Artikel möchte ich Ihnen sagen, mit welchen Methoden und Mitteln mathematische Operationen bei der Berechnung der schnellen Fourier-Transformation in einem ganzzahligen Format auf modernen FPGA-Kristallen realisiert werden. Die Basis jeder FFT ist ein Knoten, der als "Schmetterling" bezeichnet wird. Der Schmetterling implementiert mathematische Operationen - Addition, Multiplikation und Subtraktion. Es geht um die Implementierung des "Schmetterlings" und seiner fertigen Knoten, die Geschichte wird zuerst gehen. Basierend auf modernen Xilinx-FPGA-Familien - dies sind die Serien Ultrascale und Ultrascale + sowie die älteren Serien 6- (Virtex) und 7- (Artix, Kintex, Virtex) betroffen. Die älteren Serien in modernen Projekten sind 2018 nicht von Interesse. Der Zweck des Artikels besteht darin, die Merkmale der Implementierung von benutzerdefinierten Kerneln der digitalen Signalverarbeitung am Beispiel einer FFT aufzuzeigen.

Einführung

Es ist für niemanden ein Geheimnis, dass die Algorithmen für die Aufnahme von FFT fest im Leben der Ingenieure für digitale Signalverarbeitung verankert sind. Daher wird dieses Tool ständig benötigt. Führende FPGA-Hersteller wie Altera / Xilinx verfügen bereits über flexibel konfigurierbare FFT / IFFT-Kerne, weisen jedoch eine Reihe von Einschränkungen und Funktionen auf. Daher musste ich meine eigenen Erfahrungen mehr als einmal nutzen. Diesmal musste ich also eine FFT in einem ganzzahligen Format gemäß dem Radix-2-Schema auf dem FPGA implementieren. In meinem letzten Artikel habe ich bereits FFT im Gleitkommaformat durchgeführt, und von dort wissen Sie, dass der Algorithmus mit doppelter Parallelität zur Implementierung der FFT verwendet wird, dh der Kern kann zwei komplexe Abtastwerte mit derselben Frequenz verarbeiten . Dies ist eine wichtige FFT-Funktion, die in den vorgefertigten Xilinx FFT-Kerneln nicht verfügbar ist.

Beispiel: Es ist erforderlich, einen FFT-Knoten zu entwickeln, der einen kontinuierlichen Betrieb des Eingangsstroms komplexer Zahlen mit einer Frequenz von 800 MHz ausführt. Der Kern von Xilinx wird dies nicht ziehen (die erreichbaren Verarbeitungstaktfrequenzen in modernen FPGAs liegen in der Größenordnung von 300 bis 400 MHz), oder es wird erforderlich sein, den Eingangsstrom irgendwie zu dezimieren. Mit dem benutzerdefinierten Kern können Sie zwei Eingangsabtastwerte ohne vorherige Intervention mit einer Frequenz von 400 MHz anstelle eines einzelnen Abtastwerts mit 800 MHz takten. Ein weiteres Minus des Xilinx-FFT-Kerns ist die Unfähigkeit, den Eingangsstrom in Bit-umgekehrter Reihenfolge zu akzeptieren . In diesem Zusammenhang wird eine riesige FPGA-Chipspeicherressource verwendet, um Daten in einer normalen Reihenfolge neu anzuordnen. Wenn bei Aufgaben der schnellen Faltung von Signalen zwei FFT-Knoten hintereinander stehen, kann dies zu einem kritischen Moment werden, dh die Aufgabe liegt einfach nicht im ausgewählten FPGA-Chip. Mit dem benutzerdefinierten FFT-Kern können Sie Daten in der normalen Reihenfolge am Eingang empfangen und im Bit-Reverse-Modus ausgeben, während der Kern der inversen FFT Daten im Gegensatz dazu in Bit-Reverse-Reihenfolge empfängt und im normalen Modus ausgibt. Zwei Puffer für die Datenpermutation werden gleichzeitig gespeichert !!!

Da sich der größte Teil des Materials in diesem Artikel mit dem vorherigen überschneiden könnte, habe ich mich entschlossen, mich auf das Thema der mathematischen Operationen im Integer-Format auf FPGA für die Implementierung von FFT zu konzentrieren.

FFT-Kernel-Parameter

• NFFT - Anzahl der Schmetterlinge (FFT-Länge),
• DATA_WIDTH - Bittiefe der Eingabedaten (4-32),
• TWDL_WIDTH - Bittiefe der Drehfaktoren (8-27).
• SERIE - Definiert die FPGA-Familie, auf der die FFT implementiert ist („NEU“ - Ultrascale, „ALT“ - 6/7 Xilinx FPGA-Serie).

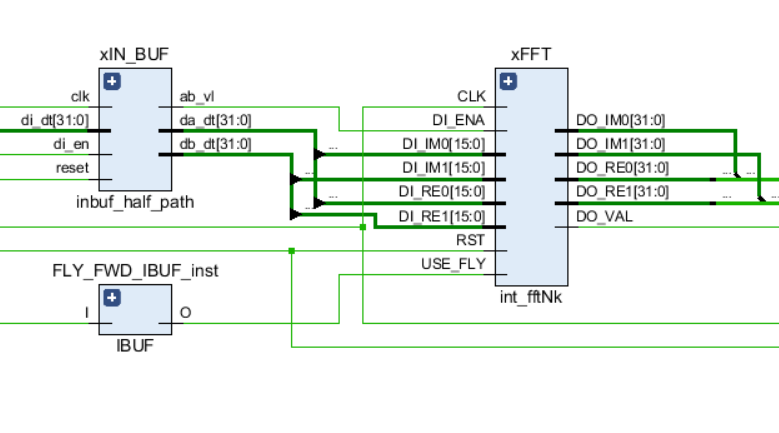
Wie alle anderen Verbindungen in der Schaltung verfügt die FFT über Eingangssteuerungsports - ein Taktsignal und einen Reset sowie Eingangs- und Ausgangsdatenports. Darüber hinaus wird im Kernel das Signal USE_FLY verwendet, mit dem Sie FFT-Schmetterlinge für Debugging-Prozesse dynamisch ausschalten oder den ursprünglichen Eingabestream anzeigen können.

Die folgende Tabelle zeigt die Menge der verwendeten FPGA-Ressourcen in Abhängigkeit von der Länge der NFFT-FFT für DATA_WIDTH = 16 und zwei Bits TWDL_WIDTH = 16 und 24 Bit.



Der Kern bei NFFT = 64K ist bei der Verarbeitungsfrequenz FREQ = 375 MHz auf einem Kintex-7-Kristall (410T) stabil.

Projektstruktur

Das schematische Diagramm des FFT-Knotens ist in der folgenden Abbildung dargestellt:


Zum besseren Verständnis der Funktionen bestimmter Komponenten werde ich eine Liste der Projektdateien und deren kurze Beschreibung in hierarchischer Reihenfolge geben:

• FFT-Kernel:
  
  • int_fftNk - FFT-Knoten, Radix-2-Schaltung, Frequenzdezimierung (DIF), Eingangsstrom ist normal, Ausgangsstrom ist bitumgekehrt.
  • int_ifftNk - OBPF- Knoten, Radix-2-Schaltung, Zeitdezimierung (DIT), Eingangsstrom ist bitumgekehrt , Ausgangsstrom ist normal.
• Schmetterlinge:
  
  
  • int_dif2_fly - Schmetterling Radix-2, Dezimierung der Frequenz,
  • int_dit2_fly - Schmetterling Radix-2, zeitliche Dezimierung,
• Komplexe Multiplikatoren:
  
  
  • int_cmult_dsp48 - allgemein konfigurierbarer Multiplikator, enthält:
  • int_cmult18x25_dsp48 - Multiplikator für kleine Bittiefen der Daten und Rotationsfaktoren,
  • int_cmult_dbl18_dsp48 - doppelter Multiplikator, Bitbreite der Drehfaktoren bis zu 18 Bit,
  • int_cmult_dbl35_dsp48 - doppelter Multiplikator, Bitbreite der Rotationsfaktoren bis zu 25 * Bits,
  • int_cmult_trpl18_dsp48 - Dreifachmultiplikator, die Kapazität der Drehfaktoren bis zu 18 Bit,
  • int_cmult_trpl52_dsp48 - Dreifachmultiplikator, die Kapazität der Rotationsfaktoren bis zu 25 * Bit,
• Multiplikatoren:
  
  
  • mlt42x18_dsp48e1 - ein Multiplikator mit Operandenbits bis zu 42 und 18 Bit basierend auf DSP48E1,
  • mlt59x18_dsp48e1 - Multiplikator mit Operandenbits bis 59 und 18 Bit basierend auf DSP48E1,
  • mlt35x25_dsp48e1 - ein Multiplikator mit Operandenbits bis zu 35 und 25 Bit basierend auf DSP48E1,
  • mlt52x25_dsp48e1 - ein Multiplikator mit Operandenbits bis zu 52 und 25 Bit basierend auf DSP48E1,
  • mlt44x18_dsp48e2 - Multiplikator mit Operandenbits bis zu 44 und 18 Bit basierend auf DSP48E2,
  • mlt61x18_dsp48e2 - Multiplikator mit Operandenbits bis 61 und 18 Bit basierend auf DSP48E2,
  • mlt35x27_dsp48e2 - Multiplikator mit Operandenbits bis zu 35 und 27 Bit basierend auf DSP48E2,
  • mlt52x27_dsp48e2 ist ein Multiplikator mit Operandenbits bis zu 52 und 27 Bit basierend auf DSP48E2.
• Summierer:
  
  
  • int_addsub_dsp48 - Universaladdierer, Operandenbits bis zu 96 Bit.
• Verzögerungsleitungen:
  
  
  • int_delay_line - die Basislinie der Verzögerung, bietet eine Permutation von Daten zwischen Schmetterlingen,
  • int_align_fft - Ausrichtung der Eingabedaten und der Drehfaktoren am Eingang des FFT-Schmetterlings,
  • int_align_fft - Ausrichtung der Eingabedaten und der Drehfaktoren am Eingang des OBPF- Schmetterlings,
• Rotierende Faktoren:
  
  
  • rom_twiddle_int - ein Generator von Rotationsfaktoren, ab einer bestimmten Länge berücksichtigt die FFT Koeffizienten basierend auf DSP-FPGA-Zellen.
  • row_twiddle_tay - Generator von Rotationsfaktoren unter Verwendung einer Taylor-Reihe (NFFT> 2K) **.
• Datenpuffer:
  
  
  • inbuf_half_path - Eingabepuffer, empfängt den Stream im normalen Modus und erzeugt zwei Sequenzen von Abtastwerten, die um die halbe Länge der FFT *** verschoben sind.
  • outbuf_half_path - Der Ausgabepuffer sammelt zwei Sequenzen und erzeugt eine kontinuierliche, die der Länge der FFT entspricht.
  • iobuf_flow_int2 - Der Puffer arbeitet in zwei Modi: Er empfängt einen Stream im Interleave-2-Modus und erzeugt zwei Sequenzen von FFT, die um die halbe Länge verschoben sind. Oder umgekehrt, abhängig von der BITREV-Option.
  • int_bitrev_ord ist ein einfacher Datenkonverter von natürlicher Reihenfolge zu Bitumkehr .

* - für DSP48E1: 25 Bit, für DSP48E2 - 27 Bit.
** - Ab einer bestimmten Stufe der FFT kann eine feste Menge an Blockspeicher zum Speichern von Rotationskoeffizienten verwendet werden, und Zwischenkoeffizienten können unter Verwendung von DSP48-Knoten unter Verwendung der Taylor-Formel zur ersten Ableitung berechnet werden. Aufgrund der Tatsache, dass die Speicherressource für die FFT wichtiger ist, können Sie Recheneinheiten sicher für den Speicher opfern.
*** - Eingangspuffer und Verzögerungsleitungen - tragen wesentlich zur Menge der belegten FPGA-Speicherressourcen bei

Schmetterling

Jeder, der mindestens einmal auf den schnellen Fourier-Transformationsalgorithmus gestoßen ist, weiß, dass dieser Algorithmus auf einer Elementaroperation basiert - einem „Schmetterling“. Es konvertiert den Eingabestream durch Multiplizieren der Eingabe mit dem Twiddle-Faktor. Es gibt zwei klassische Umwandlungsschemata für FFTs - Dezimierung in der Frequenz (DIF, Dezimierung in der Frequenz) und Dezimierung in der Zeit (DIT, Dezimierung in der Zeit). Der DIT-Algorithmus ist dadurch gekennzeichnet, dass die Eingabesequenz in zwei Sequenzen von halber Dauer und der DIF-Algorithmus in zwei Sequenzen von geraden und ungeraden Abtastwerten von NFFT-Dauer aufgeteilt wird. Darüber hinaus unterscheiden sich diese Algorithmen in mathematischen Operationen für die Schmetterlingsoperation.



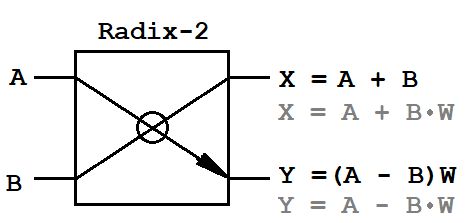A, B - Eingangspaare komplexer Proben,
X, Y - Ausgangspaare komplexer Abtastwerte,
W - komplexe Drehfaktoren.

Da die Eingabedaten komplexe Größen sind, benötigt der Schmetterling einen komplexen Multiplikator (4 Multiplikationsoperationen und 2 Additionsoperationen) und zwei komplexe Addierer (4 Additionsoperationen). Dies ist die gesamte mathematische Basis, die auf dem FPGA implementiert werden muss.

Multiplikator

Es ist zu beachten, dass alle mathematischen Operationen an FPGAs häufig in zusätzlichem Code (2er-Komplement) ausgeführt werden. Der FPGA-Multiplikator kann auf zwei Arten implementiert werden - in der Logik mithilfe von Triggern und LUT-Tabellen oder in speziellen DSP48-Berechnungseinheiten, die seit langem in allen modernen FPGAs enthalten sind. Bei logischen Blöcken wird die Multiplikation unter Verwendung des Booth-Algorithmus oder seiner Modifikationen implementiert, beansprucht eine angemessene Menge logischer Ressourcen und erfüllt nicht immer die Zeitbeschränkungen bei hohen Datenverarbeitungsfrequenzen. In dieser Hinsicht werden FPGA-Multiplikatoren in modernen Projekten fast immer auf der Basis von DSP48-Knoten und nur gelegentlich auf Logik ausgelegt. Ein DSP48-Knoten ist eine komplexe fertige Zelle, die mathematische und logische Funktionen implementiert. Grundlegende Operationen: Multiplikation, Addition, Subtraktion, Akkumulation, Zähler, logische Operationen (XOR, NAND, AND, OR, NOR), Quadrieren, Vergleichen von Zahlen, Verschieben usw. Die folgende Abbildung zeigt die DSP48E2-Zelle für die Xilinx Ultrascale + FPGA-Familie.



Durch eine einfache Konfiguration der Eingabeports, Berechnungsoperationen in Knoten und das Einstellen von Verzögerungen innerhalb des Knotens können Sie einen mathematischen Hochgeschwindigkeits-Datendrescher erstellen.
Beachten Sie, dass alle Top-FPGA-Anbieter in der Entwicklungsumgebung über Standard- und freie IP-Kerne für die Berechnung mathematischer Funktionen basierend auf dem DSP48-Knoten verfügen. Mit ihnen können Sie primitive mathematische Funktionen berechnen und verschiedene Verzögerungen am Ein- und Ausgang des Knotens einstellen. Für Xilinx ist dies der IP-Core-Multiplikator (Version 12.0, 2018), mit dem Sie den Multiplikator für eine beliebige Bittiefe von Eingabedaten von 2 bis 64 Bit konfigurieren können. Darüber hinaus können Sie angeben, wie der Multiplikator implementiert wird - auf logischen Ressourcen oder auf integrierten DSP48-Grundelementen.

Schätzen Sie, wie viel Logik der Multiplikator mit der Bittiefe der Eingangsdaten an den Ports A und B "frisst" = 64 Bit. Wenn Sie die Knoten DSP48 verwenden, benötigen sie nur 16.



Die Hauptbeschränkung bei DSP48-Zellen ist die Bittiefe der Eingabedaten. Der Knoten DSP48E1, der die Basiszelle der FPGA Xilinx 6- und 7-Serie ist, hat die Breite der Eingangsports für die Multiplikation: "A" - 25 Bit, "B" - 18 Bit. Daher ist das Ergebnis der Multiplikation eine 43-Bit-Zahl. Für die Xilinx Ultrascale- und Ultrascale + FPGA-Familie hat der Knoten mehrere Änderungen erfahren, insbesondere wurde die Kapazität des ersten Ports um zwei Bits erhöht: "A" - 27 Bits, "B" - 18 Bits. Außerdem heißt der Knoten selbst DSP48E2.

Um nicht an eine bestimmte Familie und einen bestimmten FPGA-Chip gebunden zu sein, um die „Reinheit des Quellcodes“ sicherzustellen und alle möglichen Bittiefen der Eingabedaten zu berücksichtigen, wurde beschlossen, einen eigenen Satz von Multiplikatoren zu entwerfen. Dies ermöglicht die effizienteste Implementierung komplexer Multiplikatoren für FFT-Schmetterlinge, nämlich Multiplikatoren und einen auf DSP48-Blöcken basierenden Addierer-Subtrahierer. Der erste Eingang des Multiplikators sind die Eingangsdaten, der zweite Eingang des Multiplikators sind die Drehfaktoren (harmonisches Signal aus dem Speicher). Unter Verwendung der integrierten UNISIM-Bibliothek wird eine Reihe von Multiplikatoren implementiert, aus denen die Grundelemente DSP48E1 und DSP48E2 für ihre weitere Verwendung im Projekt verbunden werden müssen. Eine Reihe von Multiplikatoren ist in der Tabelle dargestellt. Es ist zu beachten, dass:

• Die Operation des Multiplizierens von Zahlen führt zu einer Erhöhung der Kapazität des Produkts als Summe der Kapazität der Operanden.
• Jeder der Multiplikatoren 25x18 und 27x18 ist tatsächlich doppelt vorhanden - dies ist eine Komponente für verschiedene Familien.
• Je größer die Parallelitätsstufe der Operation ist, desto größer ist die Verzögerung bei der Berechnung und desto mehr Ressourcen werden belegt.
• Bei geringerer Bittiefe am Eingang „B“ können Multiplikatoren mit höherer Bittiefe am anderen Eingang implementiert werden.
• Die Hauptbeschränkung beim Erhöhen der Bittiefe wird durch Port "B" (den realen Port des DSP48-Grundelements) und das interne Schieberegister um 17 Bit eingeführt.

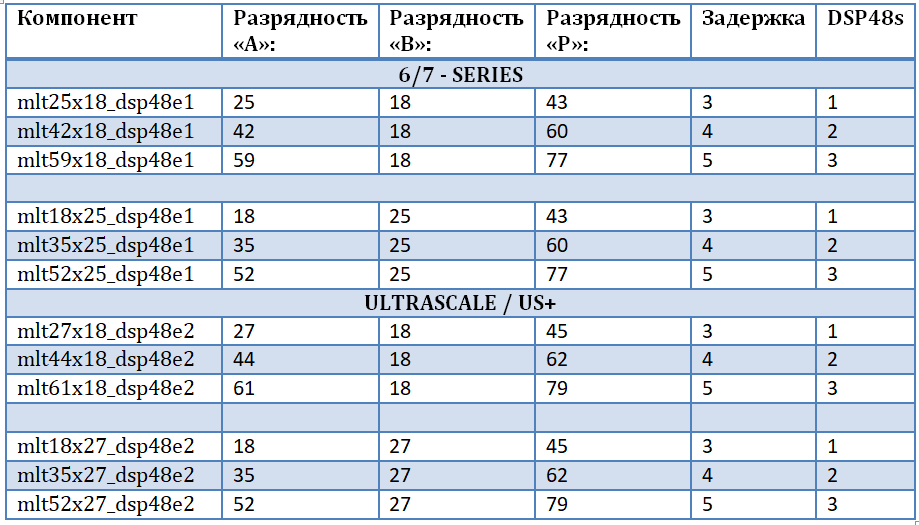
Eine weitere Erhöhung der Bittiefe ist im Rahmen der Aufgabe aus den nachfolgend beschriebenen Gründen nicht von Interesse:

Bittiefe der Drehfaktoren

Es ist bekannt, dass je größer die Auflösung des harmonischen Signals ist, desto genauer erscheint die Zahl (desto mehr Vorzeichen im Bruchteil). Die Portbitgröße beträgt jedoch B <25 Bit, da für die Rotationsfaktoren in den FFT-Knoten diese Bittiefe ausreicht, um eine qualitativ hochwertige Multiplikation des Eingangsstroms mit harmonischen Signalelementen in den „Schmetterlingen“ sicherzustellen (für alle realistisch erreichbaren FFT-Längen auf modernen FPGAs). Der typische Wert der Bittiefe der Drehkoeffizienten in den Aufgaben, die ich implementiere, ist 16 Bit, 24 - seltener, 32 - nie.

Bittiefe der Eingangsabtastwerte

Die Kapazität dieser typischen Empfangs- und Aufzeichnungsknoten (ADCs, DACs) ist nicht groß - von 8 bis 16 Bit und selten - 24 oder 32 Bit. Darüber hinaus ist es im letzteren Fall effizienter, das Gleitkomma-Datenformat gemäß dem IEEE-754-Standard zu verwenden. Andererseits fügt jede Stufe des "Schmetterlings" in der FFT aufgrund mathematischer Operationen ein Datenbit zu den Ausgangsabtastwerten hinzu. Beispielsweise wird für eine Länge von NFFT = 1024 log2 (NFFT) = 10 Schmetterlinge verwendet.

Daher ist die Ausgabebittiefe zehn Bit größer als die Eingabe, WOUT = WIN + 10. Im Allgemeinen sieht die Formel folgendermaßen aus:

WOUT = WIN + log2 (NFFT);

Ein Beispiel:

Bittiefe des Eingangsstroms WIN = 32 Bit,
Bittiefe der Drehfaktoren TWD = 27,
Die Kapazität von Port "A" aus der Liste der in diesem Artikel implementierten Multiplikatoren überschreitet 52 Bit nicht. Dies bedeutet, dass die maximale Anzahl von Schmetterlingen FFT = 52-32 = 20 beträgt. Das heißt, es ist möglich, FFT mit einer Länge von bis zu 2 ^ 20 = 1 M Proben zu realisieren. (In der Praxis ist dies jedoch aufgrund begrenzter Ressourcen selbst für die leistungsstärksten FPGA-Kristalle nicht auf direktem Wege möglich. Dies bezieht sich jedoch auf ein anderes Thema und wird im Artikel nicht berücksichtigt.)

Wie Sie sehen können, ist dies einer der Hauptgründe, warum ich keine Multiplikatoren mit höherer Bittiefe der Eingangsports implementiert habe. Die verwendeten Multiplikatoren decken den gesamten Bereich der erforderlichen Eingangsbitgrößen und Rotationsfaktoren für die Berechnung der ganzzahligen FFT ab. In allen anderen Fällen können Sie die FFT- Berechnung im Gleitkommaformat verwenden !

Die Implementierung des "breiten" Multiplikators

Anhand eines einfachen Beispiels für die Multiplikation zweier Zahlen, die nicht in die Bittiefe eines Standard-DSP48-Knotens passen, werde ich zeigen, wie Sie einen breiten Datenmultiplikator implementieren können. Die folgende Abbildung zeigt das Blockdiagramm. Der Multiplikator implementiert die Multiplikation von zwei vorzeichenbehafteten Zahlen im zusätzlichen Code, die Breite des ersten Operanden X beträgt 42 Bit, das zweite Y beträgt 18 Bit. Es enthält zwei DSP48E2-Knoten. Zwei Register werden verwendet, um Verzögerungen im oberen Knoten auszugleichen. Dies geschieht, weil Sie im oberen Addierer die Zahlen vom oberen und unteren Knoten des DSP48 korrekt hinzufügen müssen. Der untere Addierer wird eigentlich nicht verwendet. Am Ausgang des unteren Knotens gibt es eine zusätzliche Verzögerung des Produkts, um die Ausgangsnummer an der Zeit auszurichten. Die Gesamtverzögerung beträgt 4 Zyklen.



Die Arbeit besteht aus zwei Komponenten:

• Der jüngste Teil: P1 = '0' & X [16: 0] * Y [17: 0];
• Der ältere Teil: P2 = X [42:17] * Y [17: 0] + (P1 >> 17);

Summierer

Wie ein Multiplikator kann ein Addierer auf logischen Ressourcen mithilfe einer Übertragungskette oder auf DSP48-Blöcken aufgebaut werden. Um einen maximalen Durchsatz zu erzielen, ist eine zweite Methode vorzuziehen. Ein DSP48-Grundelement ermöglicht die Implementierung der Additionsoperation mit bis zu 48 Bit, zwei Knoten mit bis zu 96 Bit. Für die aktuelle Aufgabe reichen solche Bittiefen völlig aus. Darüber hinaus verfügt das DSP48-Grundelement über einen speziellen „SIMD MODE“ -Modus, der die integrierte 48-Bit-ALU in mehrere Operationen mit unterschiedlichen Daten mit geringer Kapazität parallelisiert. Das heißt, im "EINS" -Modus wird ein Vollbitgitter von 48 Bit und zwei Operanden verwendet, und im "ZWEI" -Modus wird das Bitgitter in mehrere parallele Ströme von jeweils 24 Bit (4 Operanden) unterteilt. Dieser Modus, bei dem nur ein Addierer verwendet wird, hilft, die Menge der belegten FPGA-Chipressourcen bei kleinen Bittiefen von Eingangsabtastwerten (in den ersten Berechnungsstufen) zu reduzieren.

Bittiefenerhöhung

Die Operation des Multiplizierens zweier Zahlen mit den Bits N und M in einem binären Zusatzcode führt zu einer Erhöhung der Ausgangsbitkapazität auf P = N + M.

Beispiel: Um Drei-Bit-Zahlen N = M = 3 zu multiplizieren, beträgt die maximale positive Zahl +3 = (011) ₂ und die maximale negative Zahl 4 = (100) ₂ . Das höchstwertige Bit ist für das Vorzeichen der Zahl verantwortlich. Daher ist die maximal mögliche Zahl beim Multiplizieren +16 = (010000) ₂ , was sich aus der Multiplikation zweier maximaler negativer Zahlen -4 ergibt. Die Bittiefe des Ausgangs ist gleich der Summe der Eingangsbits P = N + M = 6 Bits.

Die Addition von zwei Zahlen mit den Bits N und M im binären Zusatzcode führt zu einer Erhöhung des Ausgangsbits um ein Bit.

Beispiel: Addiere zwei positive Zahlen, N = M = 3, die maximale positive Zahl ist 3 = (011) ₂ und die maximale negative Zahl ist 4 = (100) ₂ .Das höchstwertige Bit ist für das Vorzeichen der Zahl verantwortlich. Daher ist die maximale positive Zahl 6 = (0110) ₂ und die maximale negative Zahl ist -8 = (1000) ₂ . Die Auflösung des Ausgangs erhöht sich um ein Bit.

Berücksichtigung von Algorithmusmerkmalen

Abschneiden der Bittiefe von oben:
Um die FPGA-Ressourcen im FFT-Algorithmus zu minimieren, wurde entschieden, dass beim Multiplizieren von Daten in einem Butterfly niemals die maximal mögliche negative Zahl für Drehkoeffizienten verwendet wird. Diese Änderung wirkt sich nicht nachteilig auf das Ergebnis aus. Wenn Sie beispielsweise die 16-Bit-Darstellung von Rotationsfaktoren verwenden, beträgt die Mindestanzahl -32768 = 0x8000 und die nächste -32767 = 0x8001. Der Fehler beim Ersetzen der maximalen negativen Zahl durch den nächstgelegenen Nachbarwert beträgt ~ 0,003% und ist für die Aufgabe vollständig akzeptabel.

Durch Entfernen der Mindestanzahl im Produkt aus zwei Zahlen können Sie bei jeder Iteration ein nicht verwendetes Bit höherer Ordnung reduzieren. Beispiel: Daten - 4 = (100) ₂ , Koeffizient +3 = (011) ₂. Multiplikationsergebnis = -12 = (110100) ₂ . Das fünfte Bit kann verworfen werden, weil es dupliziert das Nachbarstück, das vierte ist ein Vorzeichenbit.

Bitkürzung von unten:

Wenn Sie das Eingangssignal im „Schmetterling“ mit dem harmonischen Effekt multiplizieren, ist es natürlich nicht erforderlich, die Tiefe des Ausgangsbits in die nächsten Schmetterlinge zu ziehen, aber es ist eine Rundung oder Kürzung erforderlich. Rotierende Faktoren werden in einem praktischen M-Bit-Format dargestellt, aber in Wirklichkeit handelt es sich um einen normalen Sinus und Cosinus, die auf Eins normiert sind. Das heißt, die Zahl 0x8000 = -1 und die Zahl 0x7FFF = +1. Daher wird das Ergebnis der Multiplikation notwendigerweise auf die ursprüngliche Bittiefe der Daten abgeschnitten (dh M Bits von den Rotationsfaktoren werden von unten abgeschnitten). In allen FFT-Implementierungen, die ich zufällig gesehen habe, werden die Drehfaktoren auf die eine oder andere Weise auf 1 normalisiert. Aus dem Ergebnis der Multiplikation ist es daher notwendig, die Bits im folgenden Gitter [N + M-1-1: M-1] zu nehmen. Das höchstwertige Bit wird nicht verwendet (subtrahieren Sie die zusätzliche 1), die niedrigstwertigen werden abgeschnitten.

Das Addieren / Subtrahieren von Daten in Operationen des "Schmetterlings" wird in keiner Weise minimiert, und nur diese Operation trägt zur Erhöhung der Bittiefe der Ausgabedaten um ein Bit in jeder Stufe der Berechnung bei .

Beachten Sie, dass in der ersten Stufe des FFT-DIT-Algorithmus oder in der letzten Stufe des FFT-DIF-Algorithmus die Daten mit einem Drehfaktor mit einem Nullindex W0 = {Re, Im} = {1, 0} multipliziert werden müssen. Aufgrund der Tatsache, dass die Multiplikation mit Eins und Null primitive Operationen sind, können sie weggelassen werden. In diesem Fall ist die Operation der komplexen Multiplikation überhaupt nicht erforderlich: Die realen und imaginären Komponenten durchlaufen ohne Änderungen eine „Wendung“. In der zweiten Stufe werden zwei Koeffizienten verwendet: W0 = {Re, Im} = {1, 0} und W1 = {Re, Im} = {0, -1}. In ähnlicher Weise können Operationen auf elementare Transformationen reduziert werden und ein Multiplexer verwendet werden, um die Ausgangsabtastung auszuwählen. Auf diese Weise können Sie DSP48-Blöcke bei den ersten beiden Schmetterlingen erheblich speichern.

Der komplexe Multiplikator ist ähnlich aufgebaut - auf der Basis von Multiplikatoren und dem Addierer-Subtrahierer sind jedoch für einige Optionen für die Eingangsdatenbittiefe keine zusätzlichen Ressourcen erforderlich, die nachstehend beschrieben werden.

Die Eingangspuffer- und Verzögerungsleitungen und Kreuzschalter ähneln denen, die im vorherigen Artikel beschrieben wurden. Rotierende Faktoren werden zu ganzen Zahlen mit konfigurierbarer Bittiefe. Ansonsten gibt es keine globalen Änderungen im Design des FFT-Kerns.

Der FFT-Kern verfügt über INT_FFTK

• Vollständig verlegtes Datenverarbeitungsschema.
• NFFT-Konvertierungslänge = 8-512K Punkte.
• Flexible Einstellung der NFFT-Konvertierungslänge.
• Ganzzahliges Eingabeformat, Bitbreite ist konfigurierbar.
• Ganzzahliges Format der Rotationsfaktoren, Bitbreite ist konfigurierbar.
• .
• !
• .
• : – , -.
• : - , – .
• . Radix-2.
• NFFT *.
• .
• (Virtex-6, 7-Series, Ultrascale).
• ~375MHz Kintex-7
• – VHDL.
• bitreverse +.
• Open Source-Projekt ohne Einbeziehung von IP-Cores von Drittanbietern.

Quellcode

Der Quellcode für den FFT INTFFTK-Kernel auf VHDL (einschließlich grundlegender Operationen und einer Reihe von Multiplikatoren) und M-Skripte für Matlab / Octave sind in meinem Github-Profil verfügbar .

Fazit

Während der Entwicklung wurde ein neuer FFT-Kern entwickelt, der im Vergleich zu vergleichbaren Unternehmen eine höhere Leistung bietet. Die Kombination von FFT- und OBPF-Kernen erfordert keine Übersetzung in die natürliche Reihenfolge, und die maximale Konvertierungslänge wird nur durch FPGA-Ressourcen begrenzt. Mit der doppelten Parallelität können Sie Eingabestreams mit doppelter Frequenz verarbeiten, was IP-CORE Xilinx nicht kann. Die Bittiefe am Ausgang der ganzzahligen FFT nimmt abhängig von der Anzahl der Umwandlungsstufen linear zu.

In einem früheren Artikel habe ich über zukünftige Pläne geschrieben: FFT-Kern Radix-4, Radix-8, ultralange FFT für viele Millionen Punkte, FFT-FP32 (im IEEE-754-Format). Kurz gesagt, fast alle von ihnen sind erlaubt, aber aus dem einen oder anderen Grund können sie derzeit nicht veröffentlicht werden. Die Ausnahme ist der FFT Radix-8-Algorithmus, mit dem ich mich nicht einmal beschäftigt habe (schwierig und faul).

Nochmals danke ich dsmv2014 , der meine abenteuerlichen Ideen immer begrüßt hat. Vielen Dank für Ihre Aufmerksamkeit!

UPDATE 22.08.2018

SCALED FFT / IFFT- Option zu Quellcodes hinzugefügt . Bei jedem Schmetterling wird die Bittiefe um 1 Bit abgeschnitten (LSB abschneiden). Ausgangsbittiefe = Eingangsbittiefe.

Zusätzlich werde ich zwei Diagramme des Durchgangs eines realen Signals durch das FPGA geben, um die integrale Eigenschaft der Transformation zu zeigen, dh wie sich das Abschneiden auf das Ergebnis der Akkumulation von Fehlern am FFT-Ausgang auswirkt. Aus der Theorie ist bekannt, dass sich infolge der Fourier-Transformation das Signal-Rausch-Verhältnis verschlechtert, wenn das Eingangssignal relativ zur nicht abgeschnittenen Version abgeschnitten wird.

Beispiel: Die Amplitude der Eingangsamplitude beträgt 6 Bit. Das Signal ist eine Sinuswelle bei 128 PF-Abtastwerten. NFFT = 1024 Abtastwerte, DATA_WIDTH = 16, TWDL_WIDTH = 16.

, SCALED « » , UNSCALED .