Überblick über den Algorithmus für Vorstellungsgespräche - Set-Generierung

Hallo Habr!

Dieser Beitrag beginnt mit der Analyse von Aufgaben nach den Algorithmen, die große IT-Unternehmen (Mail.Ru Group, Google usw.) gerne Kandidaten für Interviews geben (wenn das Interview mit Algorithmen nicht gut ist, dann die Chancen, einen Job in einem Traumunternehmen zu bekommen, leider gegen Null tendieren). Erstens ist dieser Beitrag nützlich für diejenigen, die keine Erfahrung mit Olympiadenprogrammierung oder schweren Kursen wie ShAD oder LKS haben, in denen die Themen der Algorithmen ernst genug genommen werden, oder für diejenigen, die ihr Wissen in einem bestimmten Bereich auffrischen möchten.

Gleichzeitig kann nicht argumentiert werden, dass alle Aufgaben, die hier behandelt werden, sicherlich im Interview erfüllt werden. Die Ansätze, mit denen solche Aufgaben gelöst werden, sind jedoch in den meisten Fällen ähnlich.

Die Erzählung wird in verschiedene Themen unterteilt, und wir werden zunächst Mengen mit einer bestimmten Struktur generieren.

1. Beginnen wir mit dem Tastenakkordeon: Sie müssen alle korrekten Klammersequenzen mit Klammern des gleichen Typs ( was ist die richtige Klammerfolge) generieren, wobei die Anzahl der Klammern k ist.

Dieses Problem kann auf verschiedene Arten gelöst werden. Beginnen wir mit rekursiv .

Diese Methode setzt voraus, dass wir beginnen, Sequenzen aus einer leeren Liste zu durchlaufen. Nachdem die Klammer (Öffnen oder Schließen) zur Liste hinzugefügt wurde, wird der Rekursionsaufruf erneut ausgeführt und die Bedingungen werden überprüft. Wie sind die Bedingungen? Es ist notwendig, den Unterschied zwischen öffnenden und schließenden Klammern (Variable cnt ) zu überwachen. Sie können der Liste keine schließende Klammer hinzufügen, wenn dieser Unterschied nicht positiv ist, da sonst die Klammerfolge nicht mehr korrekt ist. Es bleibt, dies sorgfältig im Code zu implementieren.

 k = 6 #   init = list(np.zeros(k)) #  ,    cnt = 0 #    ind = 0 # ,       def f(cnt, ind, k, init): #  . ,     if (cnt <= k-ind-2): init[ind] = '(' f(cnt+1, ind+1, k, init) # .    ,  cnt > 0 if cnt > 0: init[ind] = ')' f(cnt-1, ind+1, k, init) #      if ind == k: if cnt == 0: print (init) 

Die Komplexität dieses Algorithmus ist $$$O ((C_k ^ {k / 2} - C_k ^ {k / 2 -1}) * k)$zusätzlicher Speicher erforderlich $$$O (k)$.

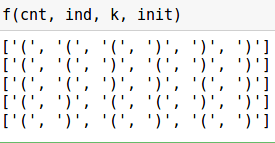
Mit den angegebenen Parametern wird der Funktionsaufruf $$$f (cnt, ind, k, init)$gibt Folgendes aus:

Ein iterativer Weg, um dieses Problem zu lösen: In diesem Fall wird die Idee grundlegend anders sein - Sie müssen das Konzept der lexikografischen Reihenfolge für Klammersequenzen einführen.

Alle korrekten Klammersequenzen für einen Klammertyp können unter Berücksichtigung der Tatsache geordnet werden, dass $$$'(' <')'$. Zum Beispiel ist für n = 6 die lexikographisch niedrigste Sequenz $$$((()))$und der älteste - $$$() () ()$.

Um die nächste lexikografische Sequenz zu erhalten, müssen Sie die am weitesten rechts stehende öffnende Klammer finden, vor der sich eine schließende Klammer befindet, damit die Klammersequenz beim Vertauschen an bestimmten Stellen korrekt bleibt. Wir tauschen sie aus und machen das Suffix zum lexikografisch kleinsten - dafür müssen Sie bei jedem Schritt die Differenz zwischen der Anzahl der Klammern berechnen.

Meiner Meinung nach ist dieser Ansatz etwas trostlos als rekursiv, aber er kann verwendet werden, um andere Probleme bei der Erzeugung von Sets zu lösen. Wir implementieren dies im Code.

 #  ,    n = 6 arr = ['(' for _ in range(n//2)] + [')' for _ in range(n//2)] def f(n, arr): #    print (arr) while True: ind = n-1 cnt = 0 #  . ,    while ind>=0: if arr[ind] == ')': cnt -= 1 if arr[ind] == '(': cnt += 1 if cnt < 0 and arr[ind] =='(': break ind -= 1 #   ,     if ind < 0: break #   .  arr[ind] = ')' #      for i in range(ind+1,n): if i <= (n-ind+cnt)/2 +ind: arr[i] = '(' else: arr[i] = ')' print (arr) 

Die Komplexität dieses Algorithmus ist dieselbe wie im vorherigen Beispiel.

Übrigens gibt es eine einfache Methode, die zeigt, dass die Anzahl der generierten Klammersequenzen für eine bestimmte n / 2 mit den katalanischen Zahlen übereinstimmen muss.

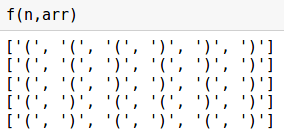
Es funktioniert!

Großartig, mit den Klammern für den Moment, lassen Sie uns fortfahren, Teilmengen zu generieren. Beginnen wir mit einem einfachen Rätsel.

2. Gegeben ein Array aufsteigender Reihenfolge mit Zahlen von $$$0$vorher $$$n-1$Es ist erforderlich, alle seine Teilmengen zu generieren.

Beachten Sie, dass die Anzahl der Teilmengen einer solchen Menge genau ist $$$2 ^ n$. Wenn jede Teilmenge als Array von Indizes dargestellt wird, wo $$$0$bedeutet, dass das Element nicht in der Menge enthalten ist, aber $$$1$- Was enthalten ist, dann wird die Erzeugung aller dieser Arrays die Erzeugung aller Teilmengen sein.

Wenn wir die bitweise Darstellung von Zahlen von 0 bis betrachten $$$2 ^ n - 1$Dann geben sie die gewünschten Teilmengen an. Das heißt, um das Problem zu lösen, ist es notwendig, die Addition von Eins zu einer Binärzahl zu implementieren. Wir beginnen mit allen Nullen und enden mit einem Array, in dem es eine Einheit gibt.

 n = 3 B = np.zeros(n+1) #  B   1  (    ) a = np.array(list(range(n))) #   def f(B, n, a): #   while B[0] == 0: ind = n #     while B[ind] == 1: ind -= 1 #   1 B[ind] = 1 #      B[(ind+1):] = 0 print (a[B[1:].astype('bool')]) 

Die Komplexität dieses Algorithmus ist $$$O (n * 2 ^ n)$aus dem Gedächtnis - $$$O (n)$.

Lassen Sie uns nun die vorherige Aufgabe etwas komplizieren.

3. Geben Sie ein geordnetes Array in aufsteigender Reihenfolge mit Zahlen von an $$$0$vorher $$$n-1$müssen Sie alles generieren $$$k$-element Teilmengen (iterativ gelöst).

Ich stelle fest, dass die Formulierung dieses Problems der vorherigen ähnlich ist und mit ungefähr der gleichen Methode gelöst werden kann: Nehmen Sie das ursprüngliche Array mit $$$k$Einheiten und $$$n-k$Nullen und sortieren nacheinander alle Varianten solcher Längenfolgen $$$n.$

Es sind jedoch geringfügige Änderungen erforderlich. Wir müssen alles sortieren $$$k$-bewertete Sätze von Zahlen aus $$$0$vorher $$$n-1$. Sie müssen genau verstehen, wie Sie die Teilmengen sortieren müssen. In diesem Fall können wir das Konzept der lexikografischen Reihenfolge für solche Mengen einführen.

Wir ordnen die Reihenfolge auch nach Zeichencodes: $$$1 <0$(Das ist natürlich seltsam, aber es ist notwendig, und jetzt werden wir verstehen, warum). Zum Beispiel für $$$n = 4, k = 2$Das jüngste und älteste wird die Sequenz sein $$$[1,1,0,0]$und $$$[0,0,1,1]$.

Es bleibt zu verstehen, wie der Übergang von einer Sequenz zur anderen beschrieben werden kann. Hier ist alles einfach: wenn wir uns ändern $$$1$auf $$$0$, dann schreiben wir links das lexikographisch minimale unter Berücksichtigung der Erhaltung des Zustands auf $$$k$. Code:

 n = 5 k = 3 a = np.array(list(range(n))) #    k -   init = [1 for _ in range(k)] + [0 for _ in range(nk)] def f(a, n, k, init): #   k-  print (a[a[init].astype('bool')]) while True: unit_cnt = 0 cur_ind = 0 #   ,     1 while (cur_ind < n) and (init[cur_ind]==1 or unit_cnt==0): if init[cur_ind] == 1: unit_cnt += 1 cur_ind += 1 #        -    if cur_ind == n: break #  init[cur_ind] = 1 #   . .  for i in range(cur_ind): if i < unit_cnt-1: init[i] = 1 else: init[i] = 0 print (a[a[init].astype('bool')]) 

Arbeitsbeispiel:

Die Komplexität dieses Algorithmus ist $$$O (C_n ^ k * n)$aus dem Gedächtnis - $$$O (n)$.

4. Gegeben ein Array aufsteigender Reihenfolge mit Zahlen von $$$0$vorher $$$n-1$müssen Sie alles generieren $$$k$-element Teilmengen (rekursiv lösen).

Versuchen wir nun die Rekursion. Die Idee ist einfach: Diesmal ohne Beschreibung, siehe Code.

 n = 5 a = np.array(list(range(n))) ind = 0 # ,       num = 0 # ,       k = 3 sub = list(-np.ones(k)) #  def f(n, a, num, ind, k, sub): #   k  ,     if ind == k: print (sub) else: for i in range(n - num): #  ,      k  if (n - num - i >= k - ind): #      sub[ind] = a[num + i] #     f(n, a, num+1+i, ind+1, k, sub) 

Arbeitsbeispiel:

Die Komplexität ist dieselbe wie bei der vorherigen Methode.

5. Gegeben ein Array aufsteigender Reihenfolge mit Zahlen von $$$0$vorher $$$n-1$ist es erforderlich, alle seine Permutationen zu erzeugen.

Wir werden mit Rekursion lösen. Die Lösung ähnelt der vorherigen, bei der wir eine Hilfsliste haben. Es ist anfangs Null, wenn eingeschaltet $$$i$-Die Stelle des Elements ist eine Einheit, dann das Element $$$i$schon in der permutation. Kaum gesagt als getan:

 a = np.array(range(3)) n = a.shape[0] ind_mark = np.zeros(n) #   perm = -np.ones(n) #     def f(ind_mark, perm, ind, n): if ind == n: print (perm) else: for i in range(n): if not ind_mark[i]: #     ind_mark[i] = 1 #   perm[ind] = i f(ind_mark, perm, ind+1, n) #   -    ind_mark[i] = 0 

Arbeitsbeispiel:

Die Komplexität dieses Algorithmus ist $$$O (n ^ 2 * n!)$aus dem Gedächtnis - $$$O (n).$

Betrachten Sie nun zwei sehr interessante Rätsel für Gray-Codes . Kurz gesagt, dies ist eine Reihe von Sequenzen gleicher Länge, wobei sich jede Sequenz in einer Kategorie von ihren Nachbarn unterscheidet.

6. Generieren Sie alle zweidimensionalen Gray-Codes der Länge n.

Die Idee, dieses Problem zu lösen, ist cool, aber wenn Sie die Lösung nicht kennen, kann es sehr schwierig sein, daran zu denken. Ich stelle fest, dass die Anzahl solcher Sequenzen ist $$$2 ^ n$.

Wir werden iterativ lösen. Angenommen, wir haben einen Teil solcher Sequenzen generiert und sie liegen in einer Liste. Wenn wir eine solche Liste duplizieren und in umgekehrter Reihenfolge schreiben, stimmt die letzte Sequenz in der ersten Liste mit der ersten Sequenz in der zweiten Liste überein, die vorletzte mit der zweiten usw. Kombinieren Sie diese Listen zu einer.

Was muss getan werden, damit sich alle Sequenzen in der Liste in derselben Kategorie voneinander unterscheiden? Platzieren Sie eine Einheit an den entsprechenden Stellen in den Elementen der zweiten Liste, um die Gray-Codes zu erhalten.

Es ist schwierig, "nach Gehör" wahrzunehmen, wir werden Iterationen dieses Algorithmus darstellen.

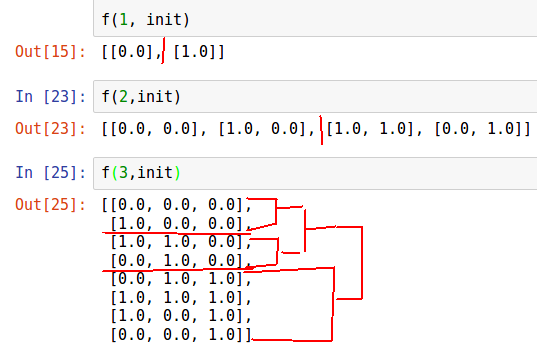
 n = 3 init = [list(np.zeros(n))] def f(n, init): for i in range(n): for j in range(2**i): init.append(list(init[2**i - j - 1])) init[-1][i] = 1.0 return init 

Die Komplexität dieser Aufgabe ist $$$O (n * 2 ^ n)$aus dem Gedächtnis das gleiche.

Lassen Sie uns nun die Aufgabe komplizieren.

7. Generieren Sie alle k-dimensionalen Gray-Codes der Länge n.

Es ist klar, dass die vergangene Aufgabe nur ein Sonderfall dieser Aufgabe ist. Auf diese schöne Weise, wie die vergangene Aufgabe gelöst wurde, kann dies jedoch nicht gelöst werden. Hier ist es notwendig, die Sequenzen in der richtigen Reihenfolge zu sortieren. Lassen Sie uns ein zweidimensionales Array erhalten $$$k * n$. Anfangs hat die letzte Zeile Einheiten und der Rest hat Nullen. Darüber hinaus ist in der Matrix $$$-1$. Hier $$$1$und $$$-1$unterscheiden sich in der Richtung: $$$1$zeigt nach oben $$$-1$zeigt nach unten. Wichtig: In jeder Spalte kann es jederzeit nur eine geben $$$1$oder $$$-1$und die restlichen Zahlen sind Nullen.

Jetzt werden wir verstehen, wie es möglich ist, diese Sequenzen zu sortieren, um Gray-Codes zu erhalten. Beginnen Sie am Ende, um das Element nach oben zu bewegen.

Im nächsten Schritt stoßen wir an die Decke. Wir schreiben die resultierende Sequenz. Nachdem Sie das Limit erreicht haben, müssen Sie mit der nächsten Spalte beginnen. Sie müssen von rechts nach links danach suchen. Wenn wir eine Spalte finden, die verschoben werden kann, ändern sich die Pfeile für alle Spalten, mit denen wir nicht arbeiten konnten, in die entgegengesetzte Richtung, damit sie wieder verschoben werden können.

Jetzt können Sie die erste Spalte nach unten verschieben. Wir bewegen es, bis es auf den Boden fällt. Und so weiter, bis alle Pfeile den Boden oder die Decke berühren und keine Säulen mehr übrig sind, die bewegt werden können.

Im Rahmen der Speichereinsparung werden wir dieses Problem jedoch mit zwei eindimensionalen Arrays mit einer Länge lösen $$$n$: In einem Array liegen die Elemente der Sequenz selbst und in der anderen Richtung (Pfeile).

 n,k = 3,3 arr = np.zeros(n) direction = np.ones(n) #   ,    def k_dim_gray(n,k): #    print (arr) while True: ind = n-1 while ind >= 0: #    ,    if (arr[ind] == 0 and direction[ind] == 0) or (arr[ind] == k-1 and direction[ind] == 1): direction[ind] = (direction[ind]+1)%2 else: break ind -= 1 #     ,     if ind < 0: break #    1 ,   1  arr[ind] += direction[ind]*2 - 1 print (arr) 

Arbeitsbeispiel:

Die Komplexität des Algorithmus ist $$$O (n * k ^ n)$aus dem Gedächtnis - $$$O (n)$.

Die Richtigkeit dieses Algorithmus wird durch Induktion am bewiesen $$$n$, hier werde ich die Beweise nicht beschreiben.

Im nächsten Beitrag werden wir die Aufgaben auf Dynamik analysieren.