Berechnung bestimmter Integrale: grundlegende Algorithmen

Diese Veröffentlichung beschreibt die einfachsten Methoden zur Berechnung der Integrale von Funktionen einer Variablen in einem Segment, auch Quadraturformeln genannt. In der Regel werden diese Methoden in mathematischen Standardbibliotheken wie der GNU Scientific Library für C, SciPy für Python und anderen implementiert. Die Veröffentlichung soll zeigen, wie diese Methoden "unter der Haube" funktionieren, und auf einige Fragen der Genauigkeit und Leistung von Algorithmen aufmerksam machen. Ich möchte auch die Beziehung von Quadraturformeln und Methoden zur numerischen Integration gewöhnlicher Differentialgleichungen erwähnen, über die ich eine weitere Veröffentlichung schreiben möchte.

Definition des Integrals

Integral (nach Riemann) einer Funktion $$$f (x)$ auf dem Segment $$$[a; b]$ Die folgende Grenze wird genannt:

wo $$$\ Delta x = \ max \ lbrace x_ {i + 1} - x_i \ rbrace$ - Feinheit der Trennwand, $$$x_0 = a$ , $$$x_n = b$ , $$$\ xi_i$ - eine beliebige Nummer im Segment $$$[x_i; x_ {i + 1}]$ .

Wenn das Integral der Funktion existiert, ist der Grenzwert unabhängig von der Partition gleich, wenn er nur ausreichend klein wäre.

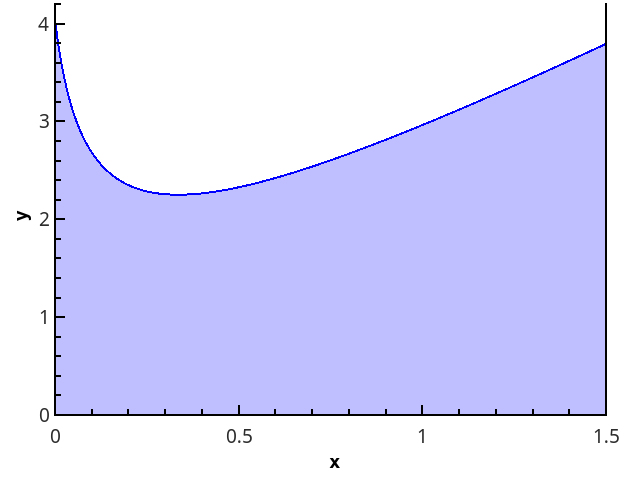
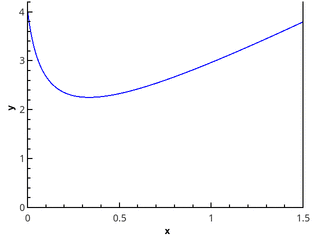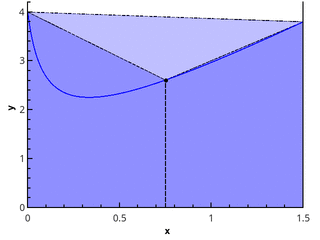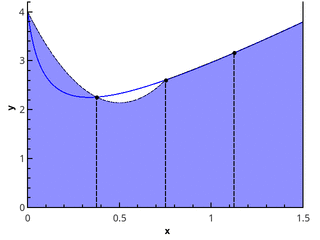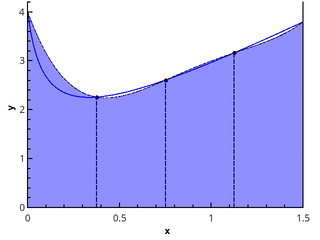
Die geometrische Definition ist klarer - das Integral entspricht der Fläche des gekrümmten Trapezes, die durch die 0 x -Achse, den Funktionsgraphen und die Geraden x = a und x = b (ausgefüllter Bereich in der Abbildung) begrenzt wird.

Quadraturformeln

Die Definition des Integrals (1) kann in der Form umgeschrieben werden

wo $$$w_i$ - Gewichtungskoeffizienten, deren Summe gleich 1 sein sollte, und die Koeffizienten selbst - tendieren mit zunehmender Zahl zu Null $$$n$ Punkte, an denen die Funktion berechnet wird.

Ausdruck (2) ist die Basis aller Quadraturformeln (d. H. Formeln zur ungefähren Berechnung des Integrals). Die Herausforderung besteht darin, Punkte auszuwählen $$$\ lbrace \ xi_i \ rbrace$ und Gewicht $$$w_i$ damit sich die Summe auf der rechten Seite dem erforderlichen Integral so genau wie möglich annähert.

Rechenaufgabe

Funktionssatz $$$f (x)$ für die es einen Algorithmus zum Berechnen von Werten an jedem Punkt im Intervall gibt $$$[a; b]$ (Ich meine die Punkte, die durch eine Gleitkommazahl dargestellt werden - dort gibt es keine Dirichlet-Funktionen !).

Es ist erforderlich, den ungefähren Wert des Integrals zu ermitteln $$$\ int_a ^ b f (x) dx$ .
Die Lösungen werden in Python 3.6 implementiert.

Verwenden Sie das Integral, um die Methoden zu überprüfen $$$\ int_0 ^ {3/2} \ left [2x + \ frac {1} {\ sqrt {x + 1/16}} \ right] dx = 17/4$ .

Stückweise konstante Approximation

Die ideal einfachen Quadraturformeln ergeben sich aus der Anwendung des Ausdrucks (1) "in der Stirn":

Weil von der Methode der Division eines Segments durch Punkte $$$\ lbrace x_i \ rbrace$ und Punkte auswählen $$$\ lbrace \ xi_i \ rbrace$ Der Grenzwert hängt nicht davon ab, dann wählen wir sie aus, damit sie bequem berechnet werden können. Beispielsweise nehmen wir die Partition einheitlich und betrachten für die Punkte der Berechnung der Funktion die Optionen: 1) $$$\ xi_i = x_i$ ;; 2) $$$\ xi_i = x_ {i + 1}$ ;; 3) $$$\ xi_i = (x_i + x_ {i + 1}) / 2$ .

Wir erhalten die Methoden für linke Rechtecke, rechte Rechtecke und Rechtecke mit einem Mittelpunkt.

def _rectangle_rule(func, a, b, nseg, frac): """  .""" dx = 1.0 * (b - a) / nseg sum = 0.0 xstart = a + frac * dx # 0 <= frac <= 1    , #    , #     dx for i in range(npoints): sum += func(xstart + i * dx) return sum * dx def left_rectangle_rule(func, a, b, nseg): """  """ return _rectangle_rule(func, a, b, nseg, 0.0) def right_rectangle_rule(func, a, b, nseg): """  """ return _rectangle_rule(func, a, b, npoints, 1.0) def midpoint_rectangle_rule(func, a, b, nseg): """    """ return _rectangle_rule(func, a, b, nseg, 0.5) 

Um die Leistung von Quadraturformeln zu analysieren, erstellen wir eine grafische Darstellung des Fehlers in den Koordinaten. "Die Anzahl der Punkte ist die Differenz zwischen dem numerischen und dem exakten Ergebnis."

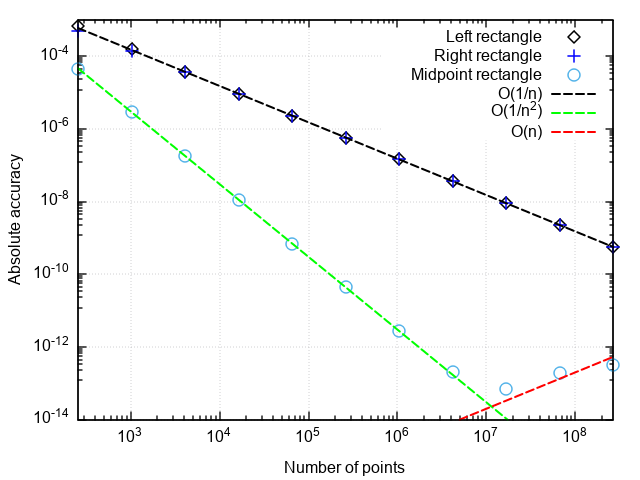
Was Sie bemerken können:

1. Eine Formel mit einem Mittelpunkt ist viel genauer als mit einem rechten oder linken Punkt
2. Der Fehler der Formel mit dem Mittelpunkt fällt schneller ab als die beiden anderen
3. Bei einer sehr kleinen Partition nimmt der Fehler der Formel mit dem Mittelpunkt zu
   Die ersten beiden Punkte beziehen sich auf die Tatsache, dass die Formel von Rechtecken mit einem Mittelpunkt eine zweite Näherungsordnung hat, d.h. $$$| I_n - I | = O (1 / n ^ 2)$ und die Formeln des rechten und linken Rechtecks ​​sind erster Ordnung, d.h. $$$| I_n - I | = O (1 / n)$ .
   Eine Zunahme des Fehlers während des Schleifens des Integrationsschritts ist mit einer Zunahme des Rundungsfehlers verbunden, wenn eine große Anzahl von Termen summiert wird. Dieser Fehler wächst wie $$$| I_n - I | = O (1 / n)$ Dies ermöglicht keine Integration, um Maschinengenauigkeit zu erreichen.
   Schlussfolgerung: Die Methoden von Rechtecken mit rechten und linken Punkten weisen eine geringe Genauigkeit auf, die mit der Verfeinerung der Partition ebenfalls langsam zunimmt. Daher sind sie nur zu Demonstrationszwecken sinnvoll. Die Methode von Rechtecken mit einem Mittelpunkt hat eine höhere Approximationsreihenfolge, wodurch sie in realen Anwendungen verwendet werden kann (mehr dazu weiter unten).

Stückweise lineare Approximation

Der nächste logische Schritt besteht darin, die integrierbare Funktion in jedem der Untersegmente durch eine lineare Funktion zu approximieren, die die Quadraturformel der Trapezien ergibt:

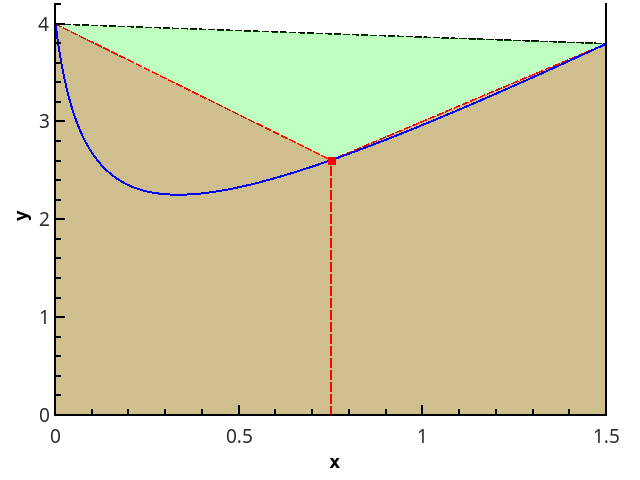
Darstellung der Trapezmethode für n = 1 und n = 2.

Bei einem einheitlichen Raster sind die Längen aller Segmente der Partition gleich und die Formel hat die Form

 def trapezoid_rule(func, a, b, nseg): """  nseg -  ,    [a;b]""" dx = 1.0 * (b - a) / nseg sum = 0.5 * (func(a) + func(b)) for i in range(1, nseg): sum += func(a + i * dx) return sum * dx 

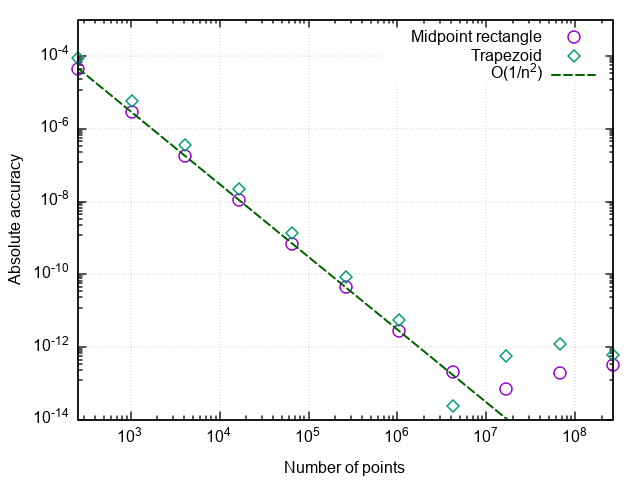
Nachdem wir den Fehler gegen die Anzahl der Teilungspunkte aufgetragen haben, sehen wir, dass die Trapezmethode auch eine zweite Näherungsordnung aufweist und im Allgemeinen geringfügig andere Ergebnisse als die Mittelpunkt-Rechteck-Methode (im Folgenden einfach die Rechteck-Methode) liefert.

Kontrolle der Berechnungsgenauigkeit

Das Einstellen der Anzahl der Teilungspunkte als Eingabeparameter ist nicht sehr praktisch, da das Integral normalerweise nicht mit einer bestimmten Partitionsdichte, sondern mit einem bestimmten Fehler berechnet werden muss. Wenn der Integrand im Voraus bekannt ist, können wir den Fehler im Voraus abschätzen und einen Integrationsschritt so wählen, dass die angegebene Genauigkeit mit Sicherheit erreicht wird. Dies ist jedoch in der Praxis selten der Fall (und ist es im Allgemeinen mit der im Voraus bekannten Funktion nicht einfacher, das Integral im Voraus zu integrieren?). Daher ist ein Verfahren zum automatischen Anpassen des Schritts an einen bestimmten Fehler erforderlich.

Wie implementiere ich das? Eine der einfachen Methoden zur Schätzung des Fehlers - die Runge-Regel - die Differenz der Werte der Integrale, berechnet aus n und 2 n Punkten, ergibt eine Fehlerschätzung: $$$\ Delta_ {2n} \ approx | I_ {2n} - I_n |$ . Die Trapezmethode ist bequemer, um die Feinheit einer Trennwand zu verdoppeln, als die Methode von Rechtecken mit einem Mittelpunkt. Bei der Berechnung nach der Trapezmethode werden neue Werte der Funktion nur in der Mitte der Segmente der vorherigen Partition benötigt, um die Anzahl der Punkte zu verdoppeln, d. H. Die vorherige Näherung des Integrals kann verwendet werden, um die nächste zu berechnen.

Von hier erhalten wir den folgenden Code für die Trapezmethode mit Präzisionskontrolle:

 def trapezoid_rule(func, a, b, rtol = 1e-8, nseg0 = 1): """  rtol -     nseg0 -    """ nseg = nseg0 old_ans = 0.0 dx = 1.0 * (b - a) / nseg ans = 0.5 * (func(a) + func(b)) for i in range(1, nseg): ans += func(a + i * dx) ans *= dx err_est = max(1, abs(ans)) while (err_est > abs(rtol * ans)): old_ans = ans ans = 0.5 * (ans + midpoint_rectangle_rule(func, a, b, nseg)) #      #       nseg *= 2 err_est = abs(ans - old_ans) return ans 

Bei diesem Ansatz wird der Integrand nicht mehrmals an einem Punkt berechnet, und alle berechneten Werte werden für das Endergebnis verwendet.

Aber ist es möglich, mit der gleichen Anzahl von Funktionsberechnungen eine höhere Genauigkeit zu erzielen? Es stellt sich heraus, dass es möglich ist, dass es Formeln gibt, die genauer als die Trapezmethode auf demselben Gitter funktionieren.

Stückweise parabolische Approximation

Der nächste Schritt besteht darin, die Funktion mit parabolischen Elementen zu approximieren. Dies erfordert, dass die Anzahl der Segmente der Partition gerade ist, dann können Parabeln durch Dreifachpunkte mit Abszissen gezogen werden {( x ₀ = a , x ₁ , x ₂ ), ( x ₂ , x ₃ , x ₄ ), ..., ( x _{n -2} , x _{n -1} , x _n = b )}.

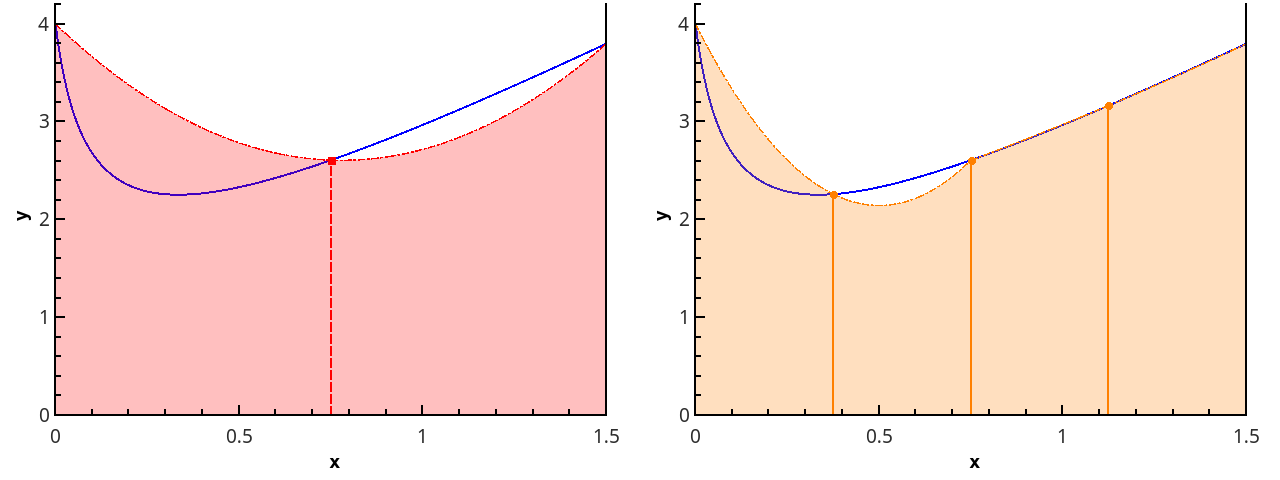
Darstellung einer stückweise parabolischen Näherung an 3 und 5 Punkten ( n = 2 und n = 3).

Annäherung an das Integral der Funktion in jedem der Segmente [ x _k ; x _{k +2} ] durch das Integral der parabolischen Approximation auf diesem Segment und unter der Annahme, dass die Punkte gleichmäßig verteilt sind ( x _{k + 1} = x _k + h ), erhalten wir die Simpson-Formel :

Formel (4) liefert direkt eine "naive" Implementierung der Simpson-Methode:

 def simpson_rule(func, a, b, nseg): """  nseg -  ,    [a;b]""" if nseg%2 = 1: nseg += 1 dx = 1.0 * (b - a) / nseg sum = (func(a) + 4 * func(a + dx) + func(b)) for i in range(1, nseg / 2): sum += 2 * func(a + (2 * i) * dx) + 4 * func(a + (2 * i + 1) * dx) return sum * dx / 3 

Um den Fehler abzuschätzen, können Sie dieselbe Berechnung des Integrals mit den Schritten h und h / 2 verwenden. Hier ist jedoch das Problem: Wenn Sie das Integral mit einem kleineren Schritt berechnen, muss das Ergebnis der vorherigen Berechnung verworfen werden, obwohl die Hälfte der neuen Funktionsberechnungen an denselben Punkten wie zuvor liegt.

Glücklicherweise können Sie vermeiden, Maschinenzeit zu verschwenden, wenn Sie die Simpson-Methode auf raffiniertere Weise implementieren. Bei näherer Betrachtung stellen wir fest, dass das Integral durch die Simpson-Formel durch zwei Integrale durch die Trapezformel mit unterschiedlichen Schritten dargestellt werden kann. Dies zeigt sich am deutlichsten im Grundfall der Approximation des Integrals über drei Punkte $$$(a, f_0), ~ (a + h, f_1), ~ (a + 2h, f_2)$ ::

Wenn wir also das Verfahren zur Halbierungsreduzierung implementieren und die letzten beiden Berechnungen nach der Trapezmethode speichern, wird die Simpson-Methode mit Genauigkeitskontrolle effizienter implementiert.

 class Quadrature: """    """ __sum = 0.0 __nseg = 1 #    __ncalls = 0 #      def __restart(func, x0, x1, nseg0, reset_calls = True): """    .       """ if reset_calls: Quadrature.__ncalls = 0 Quadrature.__nseg = nseg0 #           nseg0 Quadrature.__sum = 0.5 * (func(x0) + func(x1)) dx = 1.0 * (x1 - x0) / nseg0 for i in range(1, nseg0): Quadrature.__sum += func(x0 + i * dx) Quadrature.__ncalls += 1 + nseg0 return Quadrature.__sum * dx def __double_nseg(func, x0, x1): """  .       """ nseg = Quadrature.__nseg dx = (x1 - x0) / nseg x = x0 + 0.5 * dx i = 0 AddedSum = 0.0 for i in range(nseg): AddedSum += func(x + i * dx) Quadrature.__sum += AddedSum Quadrature.__nseg *= 2 Quadrature.__ncalls += nseg return Quadrature.__sum * 0.5 * dx def trapezoid(func, x0, x1, rtol = 1e-10, nseg0 = 1): """     . rtol -  , nseg0 -    """ ans = Quadrature.__restart(func, x0, x1, nseg0) old_ans = 0.0 err_est = max(1, abs(ans)) while (err_est > abs(rtol * ans)): old_ans = ans ans = Quadrature.__double_nseg(func, x0, x1) err_est = abs(old_ans - ans) print("Total function calls: " + str(Quadrature.__ncalls)) return ans def simpson(func, x0, x1, rtol = 1.0e-10, nseg0 = 1): """     . rtol -  , nseg0 -    """ old_trapez_sum = Quadrature.__restart(func, x0, x1, nseg0) new_trapez_sum = Quadrature.__double_nseg(func, x0, x1) ans = (4 * new_trapez_sum - old_trapez_sum) / 3 old_ans = 0.0 err_est = max(1, abs(ans)) while (err_est > abs(rtol * ans)): old_ans = ans old_trapez_sum = new_trapez_sum new_trapez_sum = Quadrature.__double_nseg(func, x0, x1) ans = (4 * new_trapez_sum - old_trapez_sum) / 3 err_est = abs(old_ans - ans) print("Total function calls: " + str(Quadrature.__ncalls)) return ans 

Vergleichen Sie die Wirksamkeit der Trapez- und Parabelmethode:

 >>> import math >>> Quadrature.trapezoid(lambda x: 2 * x + 1 / math.sqrt(x + 1 / 16), 0, 1.5, rtol=1e-9) Total function calls: 65537 4.250000001385811 >>> Quadrature.simpson(lambda x: 2 * x + 1 / math.sqrt(x + 1 / 16), 0, 1.5, rtol=1e-9) Total function calls: 2049 4.2500000000490985 

Wie Sie sehen können, kann mit beiden Methoden die Antwort mit ziemlich hoher Genauigkeit erhalten werden, aber die Anzahl der Aufrufe des Integranden ist sehr unterschiedlich - eine Methode höherer Ordnung ist 32-mal effizienter!

Durch Auftragen des Integrationsfehlers gegen die Anzahl der Schritte können wir überprüfen, ob die Approximationsreihenfolge der Simpson-Formel vier ist, d. H. numerischer Integrationsfehler $$$| I_ {Simps, n} - I | = O (1 / n ^ 4)$ (und die Integrale kubischer Polynome unter Verwendung dieser Formel werden bis zu Rundungsfehlern für jedes gerade n > 0 berechnet!).

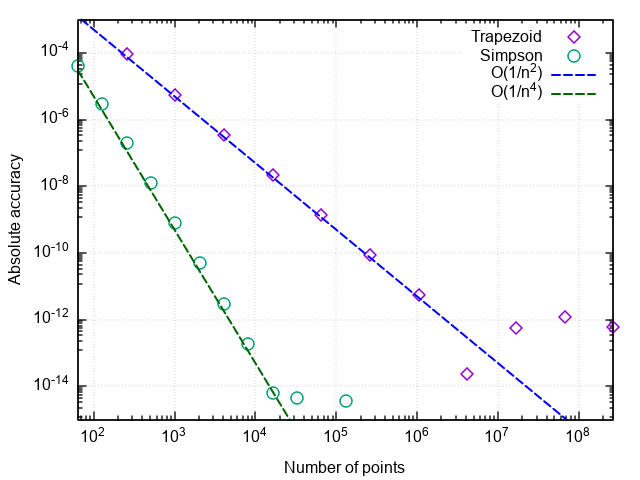
Daher ergibt sich eine solche Effizienzsteigerung im Vergleich zur einfachen Trapezformel.

Was weiter?

Die weitere Logik, die Genauigkeit von Quadraturformeln zu erhöhen, ist allgemein verständlich. Wenn wir die Funktion weiterhin mit Polynomen von immer höherem Grad approximieren, wird das Integral dieser Polynome das Integral der ursprünglichen Funktion immer genauer approximieren. Dieser Ansatz wird als Konstruktion quadratischer Newton-Cotes-Formeln bezeichnet . Formeln bis zu 8 Approximationsordnungen sind bekannt, aber die alternierenden Terme erscheinen unter den Gewichtungskoeffizienten w _i in (2), und die Formeln verlieren bei den Berechnungen an Stabilität.

Versuchen wir es andersherum. Der Fehler der Quadraturformel wird als Potenzreihe des Integrationsschritts h dargestellt . Eine bemerkenswerte Eigenschaft der Trapezmethode (und Rechtecke mit einem Mittelpunkt!) Ist, dass diese Reihe dafür nur aus geraden Graden besteht:

Die Richardson-Extrapolation basiert darauf, sukzessive Approximationen für diese Erweiterung zu finden: Anstatt den Integranden durch ein Polynom aus den berechneten Approximationen des Integrals zu approximieren $$$I (h)$ Es wird eine Polynomnäherung konstruiert, die für h = 0 die beste Annäherung an den wahren Wert des Integrals ergeben sollte.

Das Erweitern des Integrationsfehlers in geraden Potenzen des Partitionsschritts beschleunigt die Konvergenz der Extrapolation stark, weil Zur Approximation der Ordnung 2 n werden nach der Trapezmethode nur n Werte des Integrals benötigt.

Wenn wir annehmen, dass jeder nachfolgende Term kleiner als der vorherige ist, können wir nacheinander Grad von h ausschließen , wobei integrale Approximationen mit verschiedenen Schritten berechnet werden. Da die obige Implementierung es uns leicht ermöglicht, die Partition in zwei Hälften zu teilen, ist es zweckmäßig, die Formeln für die Schritte h und h / 2 zu berücksichtigen.

Es ist leicht zu zeigen, dass die Ausnahme des älteren Ausdrucks des Fehlers der Trapezformel genau die Simpson-Formel ergibt:

Wenn wir ein ähnliches Verfahren für die Simpson-Formel wiederholen, erhalten wir:

Wenn Sie fortfahren, wird die folgende Tabelle angezeigt:

Die erste Spalte enthält die nach der Trapezmethode berechneten Integrale. Wenn Sie sich von der oberen Reihe nach unten bewegen, wird die Teilung des Segments doppelt so klein, und wenn Sie sich von der linken Spalte nach rechts bewegen, nimmt die Approximationsreihenfolge des Integrals zu (d. H. Die zweite Spalte enthält die Integrale nach der Simpson-Methode usw.).

Die Elemente der Tabelle, wie aus der Erweiterung (5) abgeleitet werden kann, sind durch die Wiederholungsrelation verbunden:

Der Fehler der Approximation des Integrals kann aus der Differenz von Formeln unterschiedlicher Ordnung in einer Zeile geschätzt werden, d.h.

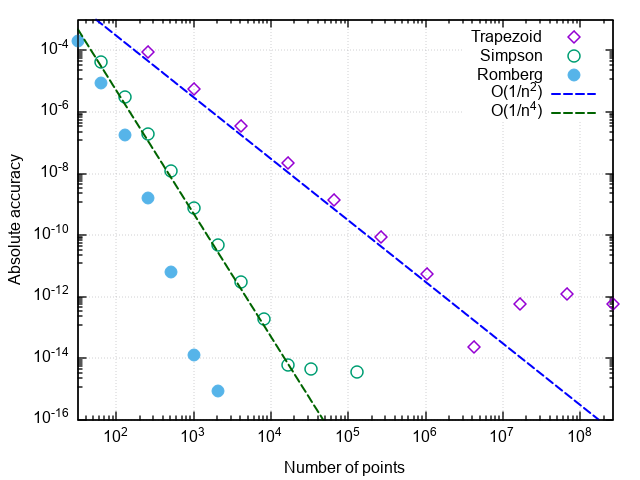
Die Verwendung der Richardson-Extrapolation zusammen mit der Trapezintegration wird als Romberg-Methode bezeichnet . Wenn die Simpson-Methode die beiden vorherigen Werte nach der Trapezmethode berücksichtigt, verwendet die Romberg-Methode alle zuvor nach der Trapezmethode berechneten Werte, um eine genauere Schätzung des Integrals zu erhalten.

 class Quadrature: """    """ __sum = 0.0 __nseg = 1 #    __ncalls = 0 #      def __restart(func, x0, x1, nseg0, reset_calls = True): """    .       """ if reset_calls: Quadrature.__ncalls = 0 Quadrature.__nseg = nseg0 #          nseg0  Quadrature.__sum = 0.5 * (func(x0) + func(x1)) dx = 1.0 * (x1 - x0) / nseg0 for i in range(1, nseg0): Quadrature.__sum += func(x0 + i * dx) Quadrature.__ncalls += 1 + nseg0 return Quadrature.__sum * dx def __double_nseg(func, x0, x1): """  .       """ nseg = Quadrature.__nseg dx = (x1 - x0) / nseg x = x0 + 0.5 * dx i = 0 AddedSum = 0.0 for i in range(nseg): AddedSum += func(x + i * dx) Quadrature.__sum += AddedSum Quadrature.__nseg *= 2 Quadrature.__ncalls += nseg return Quadrature.__sum * 0.5 * dx def romberg(func, x0, x1, rtol = 1e-10, nseg0 = 1, maxcol = 5, reset_calls = True): """   nseg0 -     maxcol -   """ #   Itable = [[Quadrature.__restart(func, x0, x1, nseg0, reset_calls)]] i = 0 maxcol = max(0, maxcol) ans = Itable[i][i] error_est = max(1, abs(ans)) while (error_est > abs(rtol * ans)): old_ans = ans i += 1 d = 4.0 ans_col = min(i, maxcol) Itable.append([Quadrature.__double_nseg(func, x0, x1)] * (ans_col + 1)) for j in range(0, ans_col): diff = Itable[i][j] - Itable[i - 1][j] Itable[i][j + 1] = Itable[i][j] + diff / (d - 1.0) d *= 4.0 ans = Itable[i][ans_col] if (maxcol <= 1): #       error_est = abs(ans - Itable[i - 1][-1]) elif (i > maxcol): error_est = abs(ans - Itable[i][min(i - maxcol - 1, maxcol - 1)]) else: error_est = abs(ans - Itable[i - 1][i - 1]) print("Total function calls: " + str(Quadrature.__ncalls)) return ans 

Lassen Sie uns überprüfen, wie die Näherung höherer Ordnung funktioniert:

 >>> Quadrature.romberg(lambda x: 2 * x + 1 / math.sqrt(x + 1/16), 0, 1.5, rtol=1e-9, maxcol = 0) #  Total function calls: 65537 4.250000001385811 >>> Quadrature.romberg(lambda x: 2 * x + 1 / math.sqrt(x + 1/16), 0, 1.5, rtol=1e-9, maxcol = 1) #  Total function calls: 2049 4.2500000000490985 >>> Quadrature.romberg(lambda x: 2 * x + 1 / math.sqrt(x + 1/16), 0, 1.5, rtol=1e-9, maxcol = 4) Total function calls: 257 4.250000001644076 

Wir sind davon überzeugt, dass sich die Anzahl der Aufrufe des Integranden im Vergleich zur Parabelmethode um das Achtfache verringert hat. Mit einer weiteren Erhöhung der erforderlichen Genauigkeit werden die Vorteile der Romberg-Methode noch deutlicher:

Einige Notizen

Bemerkung 1. Die Anzahl der Funktionsaufrufe bei diesen Problemen kennzeichnet die Anzahl der Summen bei der Berechnung des Integrals. Das Reduzieren der Anzahl von Berechnungen des Integranden spart nicht nur Rechenressourcen (obwohl dies auch bei einer optimierten Implementierung der Fall ist), sondern verringert auch die Auswirkung von Rundungsfehlern auf das Ergebnis. Wenn also versucht wird, das Integral der Testfunktion zu berechnen, friert die Trapezmethode ein, wenn versucht wird, eine relative Genauigkeit von 5 × 10 ^{-15 zu erreichen} , die Parabelmethode - mit der gewünschten Genauigkeit von 2 × 10 ^-16 (was die Grenze für Zahlen mit doppelter Genauigkeit ist), und die Romberg-Methode bewältigt die Berechnung Testintegral bis auf Maschinengenauigkeit (mit geringem Bitfehler). Das heißt, nicht nur die Genauigkeit der Integration wird für eine gegebene Anzahl von Funktionsaufrufen erhöht, sondern auch die maximal erreichbare Genauigkeit der Berechnung des Integrals.

Anmerkung 2. Wenn die Methode konvergiert, wenn eine bestimmte Genauigkeit angegeben wird, bedeutet dies nicht, dass der berechnete Wert des Integrals dieselbe Genauigkeit aufweist. Dies gilt zunächst für Fälle, in denen der angegebene Fehler nahe an der Maschinengenauigkeit liegt.

Bemerkung 3. Obwohl die Romberg-Methode für eine Reihe von Funktionen auf fast magische Weise funktioniert, wird davon ausgegangen, dass der Integrand Ableitungen hoher Ordnung begrenzt hat. Dies bedeutet, dass sich Funktionen mit Knicken oder Unterbrechungen als schlechter als einfache Methoden herausstellen können. Integrieren Sie beispielsweise f ( x ) = | x |:

 >>> Quadrature.trapezoid(abs, -1, 3, rtol=1e-5) Total function calls: 9 5.0 >>> Quadrature.simpson(abs, -1, 3, rtol=1e-5) Total function calls: 17 5.0 >>> Quadrature.romberg(abs, -1, 3, rtol=1e-5, maxcol = 2) Total function calls: 17 5.0 >>> Quadrature.romberg(abs, -1, 3, rtol=1e-5, maxcol = 3) Total function calls: 33 5.0 >>> Quadrature.romberg(abs, -1, 3, rtol=1e-5, maxcol = 4) Total function calls: 33 5.000001383269357 

Bemerkung 4. Je höher die Approximationsreihenfolge, desto besser. In der Tat ist es besser, die Anzahl der Spalten in der Romberg-Tabelle auf 4-6 zu begrenzen. Um dies zu verstehen, schauen Sie sich Formel (6) an. Der zweite Term ist die Differenz zweier aufeinanderfolgender Elemente der j-1- ten Spalte geteilt durch etwa 4 ^j . Weil Die j- te Spalte enthält Näherungen eines Integrals der Ordnung 2j , dann liegt die Differenz selbst in der Größenordnung von (1 / n _i ) ^{2 j} ~ 4 ^{- ij} . Unter Berücksichtigung der Division wird ~ 4 ^{- ( i + 1) j} ~ 4 ^{- j 2} erhalten. Das heißt, für j ~ 7 verliert der zweite Term in (6) nach der Reduzierung der Ordnungen beim Hinzufügen von Gleitkommazahlen an Genauigkeit, und eine Erhöhung der Approximationsreihenfolge kann zur Akkumulation von Rundungsfehlern führen.

Bemerkung 5. Interessenten können die beschriebenen Methoden verwenden, um das Integral aus Gründen des Interesses zu finden. $$$\ int_0 ^ 1 \ sqrt {x} \ sin {x} dx$ und gleichwertig mit ihm $$$\ int_0 ^ 1 2t ^ 2 \ sin {t ^ 2} dt$ . Wie sie sagen, fühle den Unterschied.

Fazit

Die Beschreibung und Implementierung der grundlegenden Methoden zur numerischen Integration von Funktionen in einem einheitlichen Raster wird vorgestellt. Es wird gezeigt, wie mit einer einfachen Modifikation die Klasse der Quadraturformeln unter Verwendung der Romberg-Methode auf der Basis der Trapezmethode erhalten werden kann, was die Konvergenz der numerischen Integration erheblich beschleunigt. Das Verfahren funktioniert gut zum Integrieren von "gewöhnlichen" Funktionen, d.h. schwach variierend im Integrationsintervall, ohne Singularitäten an den Rändern des Segments (siehe Bemerkung 5), schnelle Schwingungen usw.

( [3] — C++).

Literatur

1. .. , .. . . .: . 1989.
2. J. Stoer, R. Bulirsch. Introduction to Numerical Analysis: Second Edition. Springer-Verlag New York. 1993.
3. WH Press, SA Teukolsky, WT Vetterling, BP Flannery. Numerical Recipes: Third Edition. Cambridge University Press. 2007.