In Indien gibt es ein lokales Analogon unseres INN - "adhar". Das elektronische System "eAdhar" ist daran angeschraubt. In eAdhara wird jeder Buchstabe mit einem Passwort blockiert. Und alles wäre in Ordnung, aber das Passwort wird nach einem einfachen Muster erstellt: Die ersten vier Buchstaben des Namens sind Großbuchstaben plus das Geburtsjahr.
Vier Großbuchstaben und vier Zahlen. Davon können 2.821.109.909.456 Kombinationen zusammengestellt werden. Wenn Sie tausend Kombinationen pro Sekunde überprüfen, dauert ein Passwort neunzig Jahre.
Zu lang. Können wir ein paar ( Milliarden ) Mal beschleunigen?
92 Jahre → 52 Tage. Gruppe
Mit drei Billionen Kombinationen hatten wir etwas mehr. Trotzdem ist die Vorlage bekannt:
([AZ][AZ][AZ][AZ]) ([0–9][0–9][0–9][0–9]) (4 ) (4 ) ( 1) ( 2)
S2N65GE1 dieses Musters können Zeilen wie S2N65GE1 sofort verworfen werden. Wie viele Kombinationen bekommen Sie dann?
Die erste Gruppe besteht aus vier alphabetischen Zeichen. 26 Optionen, 4 Positionen erhalten wir:
4 Positionen mit 10 Ziffern, ähnlich:
Daraus erhalten wir die Gesamtzahl der Kombinationen:
Lassen Sie uns abschätzen, wie viel schneller Brute Force jetzt sein wird. Wir gehen wieder von 1000 Versuchen pro Sekunde aus:

Oder 52 Tage, 21 Stunden, 22 Minuten und 40 Sekunden. Anstelle von 92 Jahren. Nicht schlecht. Aber noch lange. Was kann man noch tun? Das Gleiche - reduzieren Sie die Anzahl der Kombinationen.
52 Tage → 12 Stunden. Schalten Sie den gesunden Menschenverstand ein
Die erste und zweite Gruppe besteht nicht aus zufälligen Zeichen, sondern aus den ersten Buchstaben des Namens und des Geburtsjahres. Beginnen wir mit dem Geburtsjahr.
Es macht keinen Sinn, Passwörter für diejenigen auszuwählen, die 1642 oder 2594 geboren wurden. So kann der Kombinationsbereich sicher von 0000–9999 auf 1918–2018 reduziert werden. Wir werden also das Plus oder Minus aller im Alter von 0 bis 100 Jahren lebenden Menschen abdecken. Dadurch werden sowohl die Anzahl der Kombinationen als auch die Zeit reduziert:

Oder 12 Stunden, 41 Minuten und 37 Sekunden.
12 Stunden → 2 Minuten. Wir opfern Genauigkeit
12 Stunden sind großartig, aber ... Wir müssen tiefer gehen .
Wir haben jetzt 45 Millionen Kombinationen, die alle eAdhara-Benutzer genau abdecken. Aber was ist, wenn sie einen kleinen Bruchteil für die Geschwindigkeitssteigerung opfern?
Wir haben digitale Kombinationen perfektioniert. Briefe machen etwas Ähnliches. Die Logik ist einfach: Es gibt kein Geburtsjahr 9999 und ebenso keinen indischen Namen mit „AAAA“ am Anfang. Aber wie werden alle geeigneten Kombinationen ermittelt?

Ich habe indische Namen von der Katalogseite gesammelt, Photon hat mir dabei sehr geholfen. Das Ergebnis sind 3.283 eindeutige Namen. Es bleiben die ersten vier Buchstaben zu kürzen und Duplikate zu entfernen:
grep -oP ”^\w{4}” custom.txt | sort | uniq | dd conv=ucase

Es stellte sich heraus, 1.598 Präfixe! Es gab einige Duplikate, da die ersten vier Buchstaben in Namen wie „Sanjeev“ und „Sanjit“ gleich sind.
1.598 Präfixe - nicht genug für eineinhalb Milliarden Menschen? Ich stimme zu. Vergessen Sie jedoch nicht, dass dies Präfixe und keine Namen sind. Ich habe die resultierende Liste auf Gist gepostet. In der Tat sollte es mehr geben. Sie können verwirrt sein, 10.000 Namen von anderen Websites sammeln und 3.000 eindeutige Präfixe erhalten, aber ich hatte keine Zeit dafür. Wir starten also ab 1.598.
Berechnen wir, wie viel Zeit jetzt benötigt wird:
Oder 2 Minuten und 39,8 Sekunden.
2 Minuten → 2 Sekunden. Wikipedia zur Rettung
2 Minuten 40 Sekunden ist die Zeit, die benötigt wird, um alle Kombinationen zu sortieren. Aber was ist, wenn die elfte Kombination richtig ist? Oder der letzte? Oder der erste?
Jetzt ist die Liste der Kombinationen alphabetisch sortiert. Aber das ist sinnlos - wer hat gesagt, dass die Namen auf „A“ häufiger sind als auf „B“ oder dass es mehr einjährige Kinder als siebzigjährige gibt?
Es ist notwendig, die Wahrscheinlichkeit jeder Kombination zu berücksichtigen. Auf Wikipedia schreiben sie:
In Indien sind mehr als 50% der Bevölkerung unter 25 und mehr als 65% unter 35 Jahre alt.
Auf dieser Grundlage können Sie anstelle der Liste 1–100 Folgendes versuchen:
25–01 ( , , ) 25–35 36–100
Dann stellt sich heraus, dass die Wahrscheinlichkeit der ersten Kombinationen steigen auf 50%. Wir haben die Hälfte der Passwörter für geknackt Sekunden! Im Folgenden Sekunden werden wir weitere 15% der Passwörter abholen. Insgesamt - 65% der Passwörter in 55,9 Sekunden.
Nun zu den Namen.
In Google ist es einfach, die TOP-100-Namen eines Landes zu finden. Basierend auf Daten aus Indien habe ich die entsprechenden Kombinationen an den Anfang der Liste verschoben. Wir gehen davon aus, dass 15% der indischen Bevölkerung populäre Namen tragen. So können 15% der Passwörter fast sofort geknackt werden.
Hindus - 80% der indischen Bevölkerung. Wenn Sie also die oben genannten hinduistischen Namen in die Liste aufnehmen, werden 80% der Versuche beschleunigt. Nach dem vorherigen Schritt sind wir gegangen Versuche. Wenn 80% von ihnen hinduistische Namen sind, dann werden 79% (wir überlassen 1% populären, aber nicht hinduistischen Namen) in den nächsten 65% der Versuche knacken.
Lassen Sie uns alles zusammen zählen und dabei die Altersstatistik berücksichtigen. In Gruppen einteilen:
100: { 50: 00 25 { 7: , 43: { 34: , 9: } } 15: 26 35 { 3: , 13*: { 10: , 3: } } 45: 36 100 { 7: , 38: { 30: , 8: } } }
Lassen Sie uns nun einen effizienten Algorithmus zum Knacken von Passwörtern erstellen:
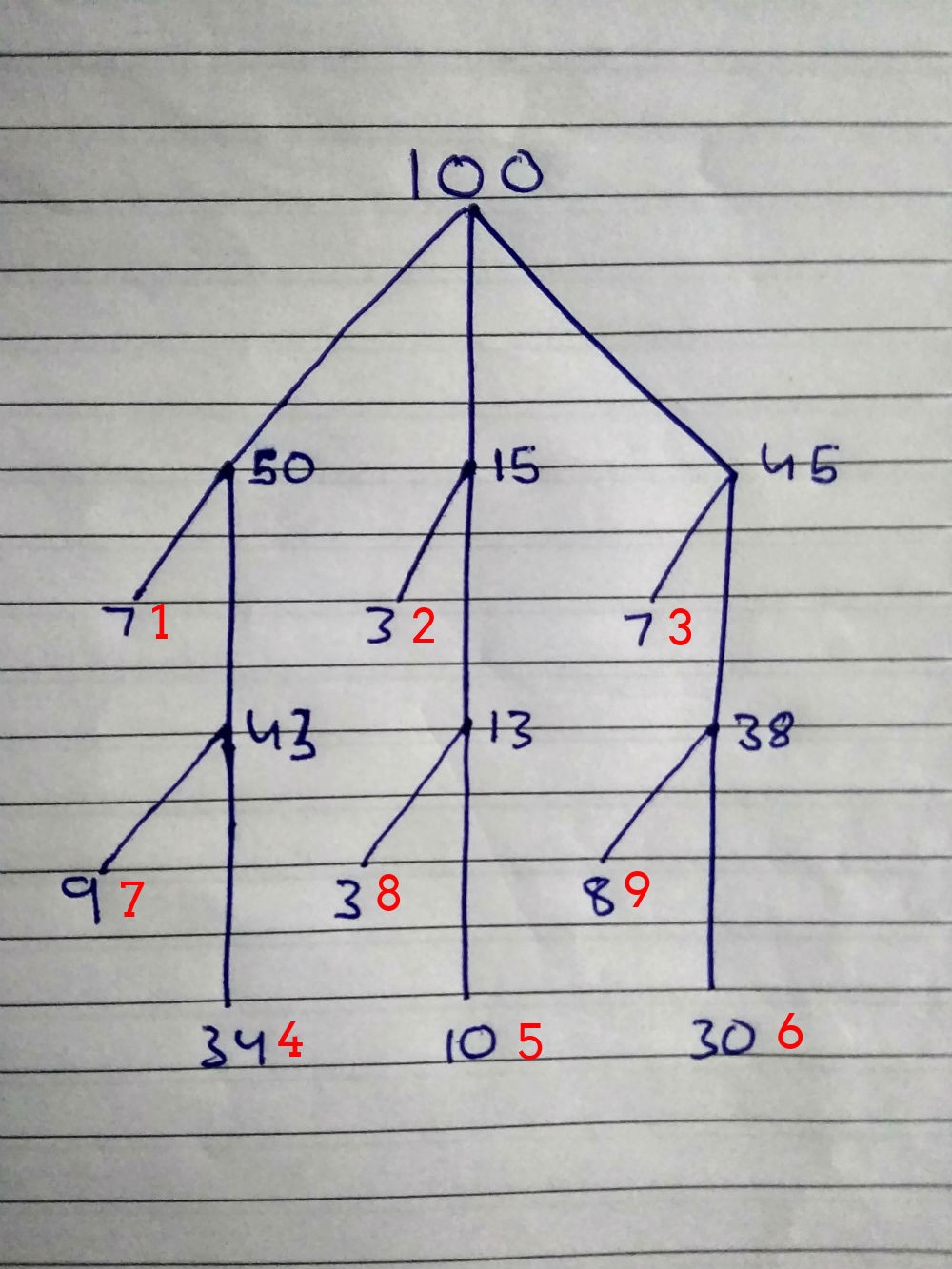
Rote Zahlen sind eine Suchpriorität. Kombinationen für Personen der ersten Gruppe werden zuerst, dann zweitens, dann drittens usw. getestet.
Wie viel Zeit braucht es jetzt, um zu hacken?
Phase 1
1 = 11 Sekunden, um 7 Passwörter zu knacken
2 = 3 Sekunden, um 3 Passwörter zu knacken
3 = 11 Sekunden, um 7 Passwörter zu knacken
Wir haben die Passwörter von 17 Personen geknackt, 83 sind geblieben. Wir werden die vorherigen Kombinationen aus der Liste entfernen und die folgenden Sätze ausprobieren - 4, 5, 6.
Phase 2
4 = 54 Sekunden, um 34 Passwörter zu knacken
5 = 16 Sekunden, um 10 Passwörter zu knacken
6 = 47 Sekunden, um 30 Passwörter zu knacken
Löschen Sie erneut die Kombinationen der vorherigen Phasen.
Phase 3
7 = 14 Sekunden, um 9 Passwörter zu knacken
8 = 5 Sekunden, um 3 Passwörter zu knacken
9 = 12 Sekunden, um 8 Passwörter zu knacken
Gesamtzeit : Sekunden oder 2 Minuten und 13 Sekunden.
Passwörter geknackt : 100
Durchschnittliche Zeit für ein Passwort : Sekunden.
92 Jahre → 1,73 Sekunden. Nitsche also, richtig?