Eine universelle Methode zum Sortieren komplexer Informationen wurde entdeckt

Wenn Sie Ihr Café öffnen, möchten Sie die Antwort auf die folgende Frage wissen: "Wo ist das andere Café diesem Punkt am nächsten?" Diese Informationen würden Ihnen helfen, Ihre Konkurrenten besser zu verstehen.

Dies ist ein Beispiel für das Suchproblem „ nächster Nachbar “, das in der Informatik umfassend untersucht wird. Wenn Sie eine Reihe von Informationen und einen neuen Punkt haben, müssen Sie herausfinden, an welchem ​​Punkt der vorhandenen der nächste ist? Eine solche Frage stellt sich in vielen alltäglichen Situationen in Bereichen wie Genomforschung, Bildsuche und Spotify-Empfehlungen.

Im Gegensatz zum Beispiel eines Cafés sind Fragen zum nächsten Nachbarn jedoch oft sehr kompliziert. In den letzten Jahrzehnten haben sich die größten Köpfe der Informatiker daran gemacht, die besten Wege zu finden, um dieses Problem zu lösen. Insbesondere versuchten sie, die Komplikationen zu bewältigen, die sich aus der Tatsache ergeben, dass es in verschiedenen Datensätzen sehr unterschiedliche Definitionen der "Nähe" von Punkten zueinander geben kann.

Und jetzt hat ein Team von Informatikern einen völlig neuen Weg gefunden, um das Problem der Suche nach dem nächsten Nachbarn zu lösen. In zwei Arbeiten haben fünf Wissenschaftler die erste verallgemeinerte Methode zur Lösung des Problems der Suche nach dem nächsten Nachbarn für komplexe Daten ausführlich beschrieben.

"Dies ist das erste Ergebnis, das mit einer einzigen algorithmischen Technik eine Vielzahl von Bereichen abdeckt ", sagte Peter Indik , IT-Spezialist am Massachusetts Institute of Technology, einer einflussreichen Persönlichkeit auf dem Gebiet der Entwicklungen im Zusammenhang mit dieser Aufgabe.

Abstandsunterschied

Wir sind so an den einzigen Weg gebunden, um die Entfernung zu bestimmen, dass es leicht ist, die Möglichkeit anderer Wege aus den Augen zu verlieren. Normalerweise messen wir den Abstand als euklidisch - als gerade Linie zwischen zwei Punkten. Es gibt jedoch Situationen, in denen andere Definitionen sinnvoller sind. Durch die Entfernung von Manhattan können Sie sich beispielsweise um 90 Grad drehen, als würden Sie sich entlang eines rechteckigen Straßennetzes bewegen. Um eine Entfernung zu messen, die 5 Kilometer in einer geraden Linie betragen kann, müssen Sie möglicherweise die Stadt 3 km in eine Richtung und dann 4 weitere in die andere Richtung durchqueren.

Es ist auch möglich, über Entfernungen zu sprechen, die nicht geografisch sind. Wie groß ist der Abstand zwischen zwei Personen in einem sozialen Netzwerk oder zwei Filmen oder zwei Genomen? In diesen Beispielen gibt der Abstand den Ähnlichkeitsgrad an.

Es gibt Dutzende von Entfernungsmetriken, von denen jede für eine bestimmte Aufgabe geeignet ist. Nehmen Sie zum Beispiel zwei Genome. Biologen vergleichen sie mit dem " Levenshtein-Abstand " oder dem Bearbeitungsabstand. Der Bearbeitungsabstand zwischen zwei Genomsequenzen ist die Anzahl der Additionen, Deletionen, Insertionen und Substitutionen, die erforderlich sind, um eine von ihnen in eine andere umzuwandeln.

Das Bearbeiten der Distanz und die euklidische Distanz sind zwei verschiedene Konzepte der Distanz, und es ist unmöglich, eine auf die andere zu reduzieren. Diese Inkompatibilität besteht für viele Paare von Entfernungsmetriken und ist ein Hindernis für Informatiker, die versuchen, Algorithmen zum Auffinden des nächsten Nachbarn zu entwickeln. Dies bedeutet, dass ein Algorithmus, der für eine Art von Entfernung funktioniert, für eine andere nicht funktioniert - genauer gesagt, bis eine neue Art von Suche erschien.


Alexander Andoni

Kreis im Quadrat

Der Standardansatz zum Finden des nächsten Nachbarn besteht darin, vorhandene Daten in Untergruppen aufzuteilen. Wenn Ihre Daten beispielsweise den Standort der Kühe auf der Weide beschreiben, können Sie sie jeweils in einen Kreis einschließen. Dann stellen wir eine neue Kuh auf die Wiese und stellen die Frage: In welchen Kreis fällt sie? Es ist praktisch garantiert, dass sich der nächste Nachbar der neuen Kuh im selben Kreis befindet.

Dann wiederholen Sie den Vorgang. Teilen Sie die Kreise in Unterkreise, teilen Sie diese Zellen weiter und so weiter. Infolgedessen gibt es eine Zelle mit nur zwei Punkten: dem vorhandenen und dem neuen. Dieser vorhandene Punkt wird Ihr nächster Nachbar sein.


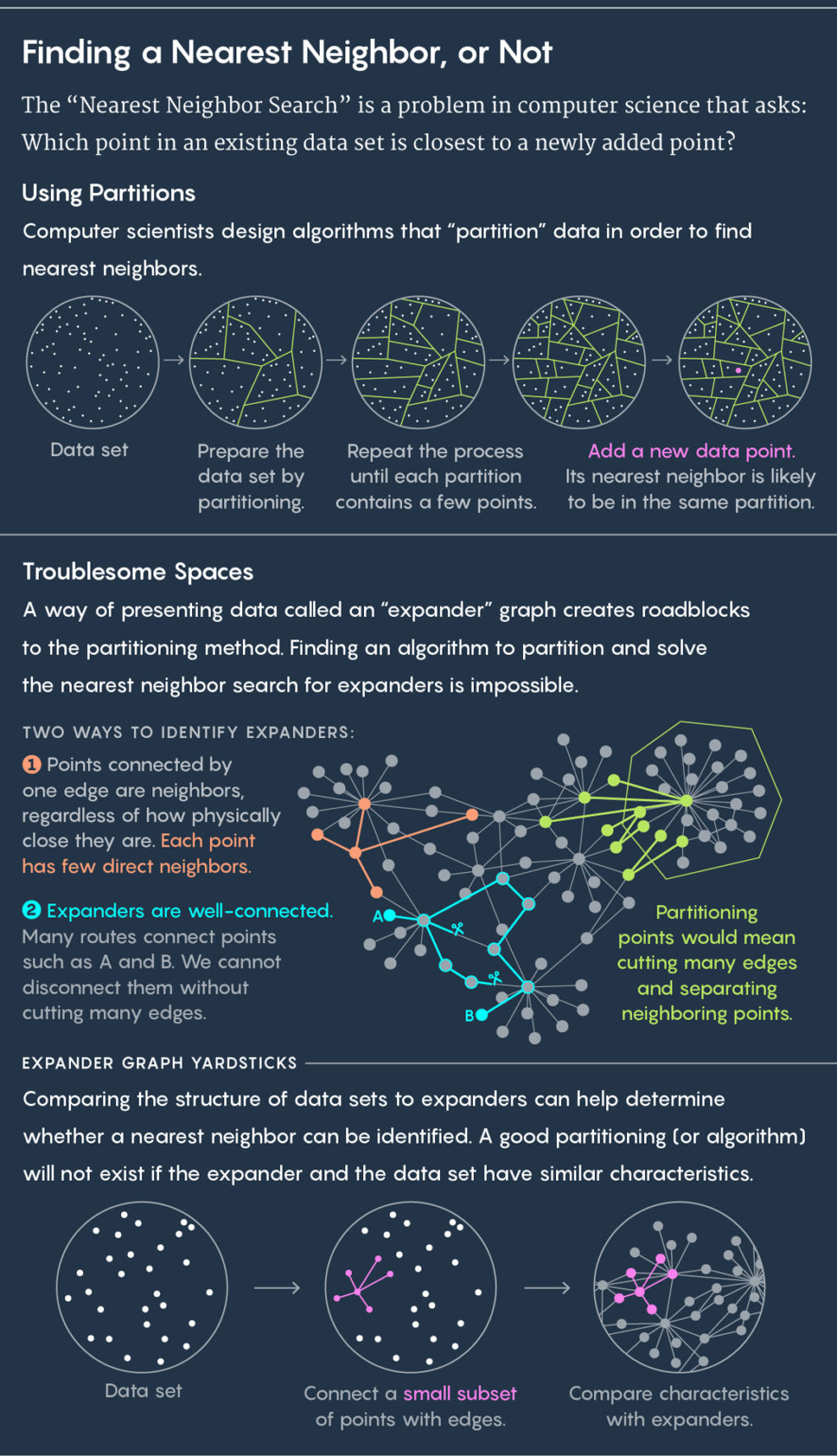Oben ist die Aufteilung der Daten in Zellen. Nachfolgend finden Sie die Verwendung des Erweiterungsdiagramms.

Algorithmen zeichnen Zellen, gute Algorithmen zeichnen sie schnell und gut - das heißt, es gibt keine Situation, in der eine neue Kuh in einen Kreis fällt und ihr nächster Nachbar in einem anderen Kreis landet. "Wir möchten, dass die Nahpunkte in diesen Zellen häufiger im selben Laufwerk miteinander auftreten und die entfernten selten sind", sagte Ilya Razenshtein , Informatikspezialistin bei Microsoft Research, Mitautorin der neuen Arbeit, an der auch Alexander Andoni von der Columbia University beteiligt war , Assaf Naor aus Princeton, Alexander Nikolov von der University of Toronto und Eric Weingarten von der Columbia University.

Seit vielen Jahren haben Informatiker verschiedene Algorithmen zum Zeichnen solcher Zellen entwickelt. Für kleine Daten - wie zum Beispiel, wo ein Punkt durch eine kleine Anzahl von Werten bestimmt wird, zum Beispiel die Position einer Kuh auf einer Weide - erzeugen Algorithmen die sogenannten „ Voronoi-Diagramme “, die die Frage nach dem nächsten Nachbarn genau beantworten.

Für mehrdimensionale Daten, bei denen ein Punkt durch Hunderte oder Tausende von Werten bestimmt werden kann, erfordern Voronoi-Diagramme zu viel Rechenleistung. Stattdessen zeichnen Programmierer Zellen mit „ lokal sensitivem Hashing “, das erstmals 1998 von Indik und Rajiv Motwani beschrieben wurde. LF-Algorithmen zeichnen Zellen zufällig. Daher arbeiten sie schneller, aber weniger genau - anstatt den genauen nächsten Nachbarn zu finden, garantieren sie, dass sich ein Punkt nicht weiter als eine bestimmte Entfernung vom tatsächlichen nächsten Nachbarn befindet. Dies kann man sich als Netflix-Filmempfehlung vorstellen, die nicht perfekt, aber gut genug ist.

Seit Ende der neunziger Jahre haben Informatiker LF-Algorithmen entwickelt, die ungefähre Lösungen für die Aufgabe bieten, den nächsten Nachbarn für bestimmte Entfernungsmetriken zu finden. Die Algorithmen waren sehr spezialisiert, und der für eine Entfernungsmetrik entwickelte Algorithmus konnte nicht für eine andere verwendet werden.

„In bestimmten Fällen kann man einen sehr effektiven Algorithmus für die euklidische oder Manhattan-Distanz entwickeln. Wir hatten jedoch keinen Algorithmus, der für eine große Klasse von Entfernungen geeignet war “, sagte Indik.

Da Algorithmen, die mit einer Metrik arbeiten, nicht für eine andere verwendet werden konnten, entwickelten Programmierer eine Problemumgehungsstrategie. Durch einen Prozess namens "Einbetten" haben sie der Metrik, für die sie war, eine Metrik auferlegt, für die sie keinen guten Algorithmus hatten. Die Übereinstimmung der Metriken war jedoch normalerweise ungenau - so etwas wie ein quadratischer Stift in einem runden Loch. In einigen Fällen funktionierte das Einbetten überhaupt nicht. Es war notwendig, einen universellen Weg zu finden, um die Frage nach dem nächsten Nachbarn zu beantworten.


Ilya Razenshtein

Unerwartetes Ergebnis

In einer neuen Arbeit gaben Wissenschaftler die Suche nach speziellen Algorithmen auf. Stattdessen stellten sie eine breitere Frage: Was verhindert die Entwicklung eines Algorithmus für eine bestimmte Entfernungsmetrik?

Sie entschieden, dass die unangenehme Situation, die mit dem expandierenden Graphen oder Expander verbunden war, schuld war. Ein Expander ist eine spezielle Art von Grafik, eine Reihe von Punkten, die durch Kanten verbunden sind. Diagramme haben ihre eigene Entfernungsmetrik. Der Abstand zwischen zwei Punkten des Diagramms ist die Mindestanzahl von Linien, die erforderlich sind, um von einem Punkt zum anderen zu gelangen. Sie können sich ein Diagramm vorstellen, das die Verbindungen zwischen Personen in sozialen Netzwerken darstellt. Der Abstand zwischen Personen entspricht dann der Anzahl der Verbindungen, die sie trennen. Wenn Julian Moore zum Beispiel einen Freund hat, der einen Freund hat, der Kevin Bacon als Freund hat, dann beträgt die Entfernung von Moore nach Bacon drei.

Ein Expander ist ein spezieller Diagrammtyp, der auf den ersten Blick zwei widersprüchliche Eigenschaften aufweist. Es verfügt über eine hohe Konnektivität, dh zwei Punkte können nicht getrennt werden, ohne mehrere Kanten zu schneiden. Gleichzeitig sind die meisten Punkte mit einer sehr kleinen Anzahl anderer verbunden. Aus diesem Grund sind die meisten Punkte weit voneinander entfernt.

Eine einzigartige Kombination dieser Eigenschaften - gute Konnektivität und eine geringe Anzahl von Kanten - führt dazu, dass es bei Expandern unmöglich ist, schnell nach dem nächsten Nachbarn zu suchen. Jeder Versuch, es in Zellen zu teilen, trennt Punkte, die nahe beieinander liegen.

„Um den Expander in zwei Teile zu schneiden, müssen mehrere Rippen geschnitten werden, wodurch viele eng beieinander liegende Eckpunkte geteilt werden“, sagte Weingarten, Mitautor der Arbeit.

Im Sommer 2016 wussten Andoni, Nyokolov, Rasenstein und Vanguarten, dass man für Expander keinen guten Algorithmus finden konnte, um den nächsten Nachbarn zu finden. Sie wollten jedoch beweisen, dass es unmöglich ist, solche Algorithmen für viele andere Entfernungsmetriken zu konstruieren - Metriken, wenn nach guten Algorithmen gesucht wird, für die Informatiker zum Stillstand gekommen sind.

Um Beweise für die Unmöglichkeit solcher Algorithmen zu finden, mussten sie einen Weg finden, die Expander-Metrik in andere Entfernungsmetriken einzubetten. Mit dieser Methode könnten sie feststellen, dass andere Metriken ähnliche Eigenschaften wie Expander-Eigenschaften haben, was sie daran hindert, gute Algorithmen zu erstellen.


Eric Weingarten

Vier Informatiker gingen zu Assaf Naoru, einem Mathematiker der Princeton University, dessen frühere Arbeit gut zum Thema Expander passte. Sie baten ihn zu helfen, zu beweisen, dass Expander in verschiedene Arten von Metriken eingebettet werden können. Naor kehrte schnell mit einer Antwort zurück - aber nicht die, die sie von ihm erwartet hatten.

"Wir haben Assaf gebeten, uns bei dieser Aussage zu helfen, und er hat das Gegenteil bewiesen", sagte Andoni.

Naor hat bewiesen, dass Expander nicht in eine große Klasse von Entfernungsmetriken passen, die als „ normierte Räume “ bezeichnet werden (zu denen auch Metriken wie euklidische und Manhattan-Räume gehören). Basierend auf Naors Beweisen folgten die Wissenschaftler der folgenden logischen Kette: Wenn Expander nicht in die Entfernungsmetrik passen, sollte es eine gute Möglichkeit geben, sie in Zellen zu zerlegen (da, wie sie bewiesen haben, die Eigenschaften von Expandern das einzige Hindernis dafür sind). Daher muss es einen guten Algorithmus geben, um den nächsten Nachbarn zu finden - auch wenn noch niemand ihn gefunden hat.

Fünf Forscher veröffentlichten ihre Ergebnisse in einem Artikel , den sie im November fertiggestellt und im April hochgeladen hatten. Es folgte eine zweite Arbeit, die sie in diesem Jahr fertigstellten und im August veröffentlichten. Darin verwendeten sie die Informationen, die sie beim Schreiben der ersten Arbeit erhalten hatten, um einen schnellen Algorithmus zum Finden des nächsten Nachbarn für normierte Räume zu finden.

"Die erste Arbeit hat gezeigt, dass es eine Möglichkeit gibt, die Metrik in zwei Teile zu teilen, aber es gab kein Rezept dafür, wie man es schnell macht", sagte Weingarten. "In der zweiten Arbeit argumentieren wir, dass es eine Möglichkeit gibt, die Punkte zu trennen, und dass diese Trennung außerdem mit schnellen Algorithmen erfolgen kann."

Infolgedessen verallgemeinern neue Arbeiten zum ersten Mal die Suche nach dem nächsten Nachbarn in mehrdimensionalen Daten. Anstatt spezielle Algorithmen für bestimmte Metriken zu entwickeln, haben Programmierer einen universellen Ansatz zum Auffinden von Algorithmen.

"Dies ist eine geordnete Methode zur Entwicklung von Algorithmen zum Finden des nächsten Nachbarn in einer der von Ihnen benötigten Entfernungsmetriken", sagte Weingarten.