
Jetzt reden alle viel über künstliche Intelligenz und ihre Anwendung in allen Bereichen des Unternehmens. Es gibt jedoch einige Bereiche, in denen seit der Antike ein Modelltyp dominiert hat, die sogenannte „White Box“ - die logistische Regression. Ein solcher Bereich ist die Bewertung von Bankkrediten.
Dafür gibt es mehrere Gründe:
- Regressionskoeffizienten können im Gegensatz zu „Black Boxes“ wie Boosting, die mehr als 500 Variablen enthalten können, leicht erklärt werden
- Maschinelles Lernen wird vom Management aufgrund der Schwierigkeit bei der Interpretation von Modellen immer noch nicht als vertrauenswürdig eingestuft
- Es gibt ungeschriebene Anforderungen der Regulierungsbehörde an die Interpretierbarkeit von Modellen: Beispielsweise kann die Zentralbank jederzeit um eine Erklärung bitten - warum ein Darlehen an den Kreditnehmer abgelehnt wurde
- Unternehmen verwenden externe Data Mining-Programme (z. B. Rapid Miner, SAS Enterprise Miner, STATISTICA oder ein anderes Paket), mit denen Sie schnell lernen können, wie Sie Modelle ohne Programmierkenntnisse erstellen
Diese Gründe machen es in einigen Bereichen fast unmöglich, komplexe Modelle des maschinellen Lernens zu verwenden. Daher ist es wichtig, das Maximum aus einer einfachen logistischen Regression herauszuholen, die leicht zu erklären und zu interpretieren ist.
In diesem Beitrag werden wir darüber sprechen, wie wir beim Erstellen von Scoring externe Data Mining-Pakete zugunsten von Open Source-Lösungen in Form von Python aufgegeben, die Entwicklungsgeschwindigkeit um ein Vielfaches erhöht und auch die Qualität aller Modelle verbessert haben.
Bewertungsprozess
Der klassische Prozess der Erstellung von Bewertungsmodellen für die Regression sieht folgendermaßen aus:
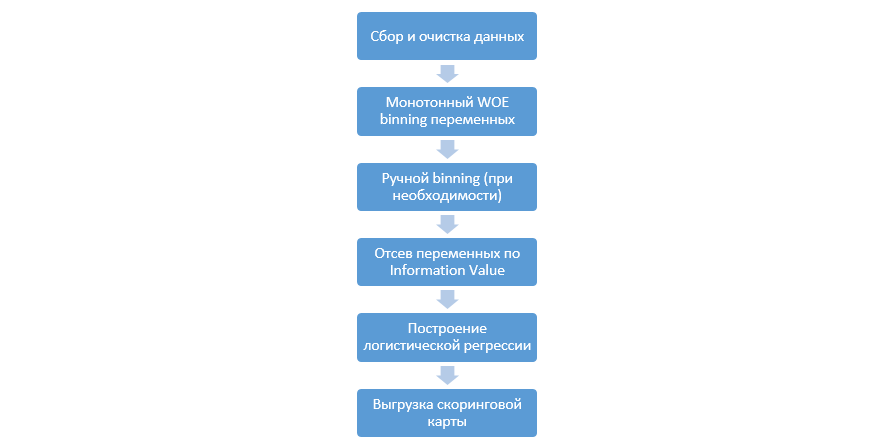
Es kann von Unternehmen zu Unternehmen unterschiedlich sein, aber die Hauptphasen bleiben konstant. Wir müssen immer eine Gruppierung von Variablen durchführen (im Gegensatz zum Paradigma des maschinellen Lernens, bei dem in den meisten Fällen nur eine kategoriale Codierung erforderlich ist), deren Überprüfung anhand des Informationswerts (IV) und das manuelle Hochladen aller Koeffizienten und Klassen für die spätere Integration in DSL.
Dieser Ansatz zum Erstellen von Scoring-Karten hat in den 90er Jahren gut funktioniert, aber die Technologien klassischer Data Mining-Pakete sind sehr veraltet und erlauben nicht die Verwendung neuer Techniken, wie beispielsweise die L2-Regularisierung bei der Regression, die die Qualität von Modellen erheblich verbessern kann.
Als Studie haben wir uns einmal entschlossen, alle Schritte, die Analysten beim Erstellen von Scores ausführen, zu reproduzieren, sie mit dem Wissen von Data Scientists zu ergänzen und den gesamten Prozess so weit wie möglich zu automatisieren.
Python-Verbesserung
Als Entwicklungswerkzeug haben wir Python wegen seiner Einfachheit und guten Bibliotheken ausgewählt und begonnen, alle Schritte der Reihe nach zu spielen.
Der erste Schritt besteht darin, Daten zu sammeln und Variablen zu generieren - diese Phase ist ein wesentlicher Bestandteil der Arbeit von Analysten.
In Python können Sie gesammelte Daten mit pymysql aus der Datenbank laden.
Code zum Herunterladen aus der Datenbankdef con(): conn = pymysql.connect( host='10.100.10.100', port=3306, user='******* ', password='*****', db='mysql') return conn; df = pd.read_sql(''' SELECT * FROM idf_ru.data_for_scoring ''', con=con())
Als nächstes ersetzen wir die seltenen und fehlenden Werte durch eine separate Kategorie, um eine Überanpassung zu verhindern, wählen das Ziel aus, löschen die zusätzlichen Spalten und teilen sie nach Zug und Test.
Datenaufbereitung def filling(df): cat_vars = df.select_dtypes(include=[object]).columns num_vars = df.select_dtypes(include=[np.number]).columns df[cat_vars] = df[cat_vars].fillna('_MISSING_') df[num_vars] = df[num_vars].fillna(np.nan) return df def replace_not_frequent(df, cols, perc_min=5, value_to_replace = "_ELSE_"): else_df = pd.DataFrame(columns=['var', 'list']) for i in cols: if i != 'date_requested' and i != 'credit_id': t = df[i].value_counts(normalize=True) q = list(t[t.values < perc_min/100].index) if q: else_df = else_df.append(pd.DataFrame([[i, q]], columns=['var', 'list'])) df.loc[df[i].value_counts(normalize=True)[df[i]].values < perc_min/100, i] =value_to_replace else_df = else_df.set_index('var') return df, else_df cat_vars = df.select_dtypes(include=[object]).columns df = filling(df) df, else_df = replace_not_frequent_2(df, cat_vars) df.drop(['credit_id', 'target_value', 'bor_credit_id', 'bchg_credit_id', 'last_credit_id', 'bcacr_credit_id', 'bor_bonuses_got' ], axis=1, inplace=True) df_train, df_test, y_train, y_test = train_test_split(df, y, test_size=0.33, stratify=df.y, random_state=42)
Jetzt beginnt die wichtigste Phase bei der Bewertung der Regression - Sie müssen WOE-Binning für numerische und kategoriale Variablen schreiben. Im öffentlichen Bereich fanden wir keine guten und geeigneten Optionen für uns und beschlossen, selbst zu schreiben.
Dieser Artikel von 2017 wurde als Grundlage für das numerische Binning verwendet, ebenso wie
dieser kategorische Artikel, den sie selbst von Grund auf neu geschrieben haben. Die Ergebnisse waren beeindruckend (Gini im Test stieg im Vergleich zu den Binning-Algorithmen externer Data Mining-Programme um 3-5).
Danach können Sie sich die Grafiken oder Tabellen ansehen (die wir dann in Excel schreiben), wie die Variablen in Gruppen unterteilt sind, und die Monotonie überprüfen:
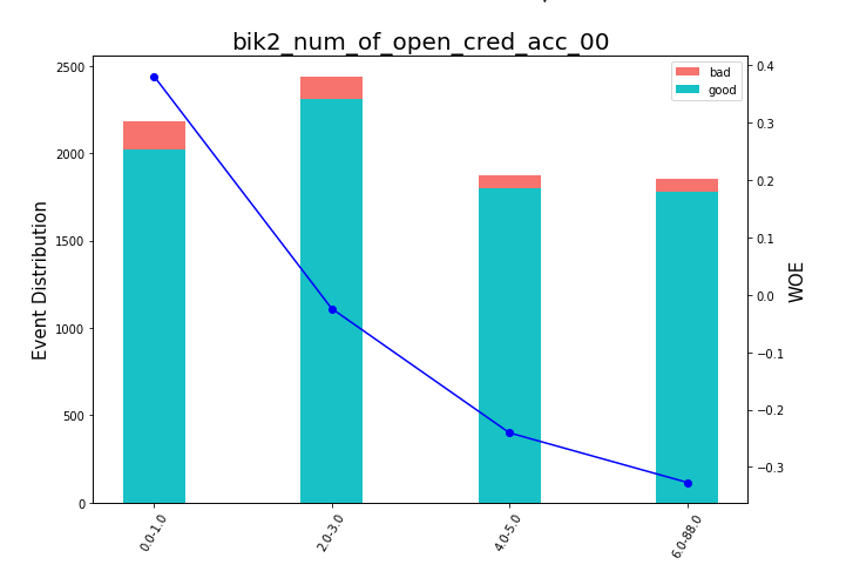
Bean Charts rendern def plot_bin(ev, for_excel=False): ind = np.arange(len(ev.index)) width = 0.35 fig, ax1 = plt.subplots(figsize=(10, 7)) ax2 = ax1.twinx() p1 = ax1.bar(ind, ev['NONEVENT'], width, color=(24/254, 192/254, 196/254)) p2 = ax1.bar(ind, ev['EVENT'], width, bottom=ev['NONEVENT'], color=(246/254, 115/254, 109/254)) ax1.set_ylabel('Event Distribution', fontsize=15) ax2.set_ylabel('WOE', fontsize=15) plt.title(list(ev.VAR_NAME)[0], fontsize=20) ax2.plot(ind, ev['WOE'], marker='o', color='blue')
Eine Funktion zum manuellen Binning wurde separat geschrieben, was beispielsweise bei der Variablen „OS-Version“ nützlich ist, bei der alle Android- und iOS-Telefone manuell gruppiert wurden.
Manuelle Binning-Funktion def adjust_binning(df, bins_dict): for i in range(len(bins_dict)): key = list(bins_dict.keys())[i] if type(list(bins_dict.values())[i])==dict: df[key] = df[key].map(list(bins_dict.values())[i]) else:
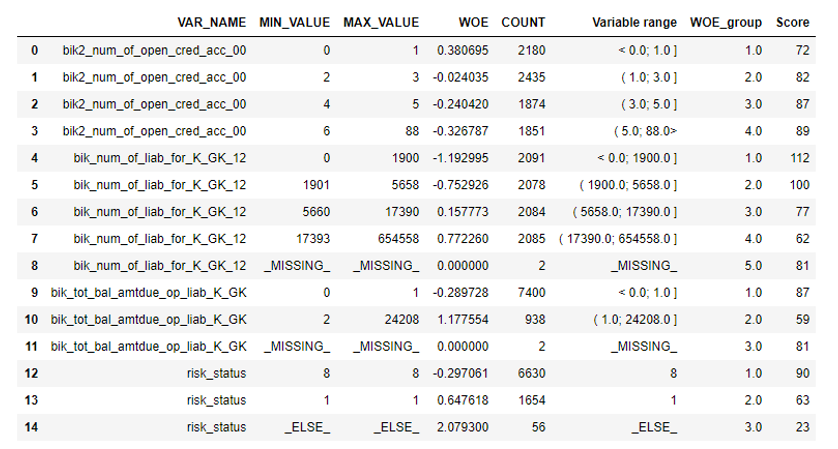
Der nächste Schritt ist die Auswahl der Variablen nach Informationswert. Der Standardwert ist 0,1 (alle unten aufgeführten Variablen haben keine gute Vorhersagekraft).
Nach der Überprüfung auf Korrelation wurde durchgeführt. Von den beiden korrelierenden Variablen müssen Sie die mit weniger IV entfernen. Die abgeschnittene Entfernung wurde 0,75 genommen.
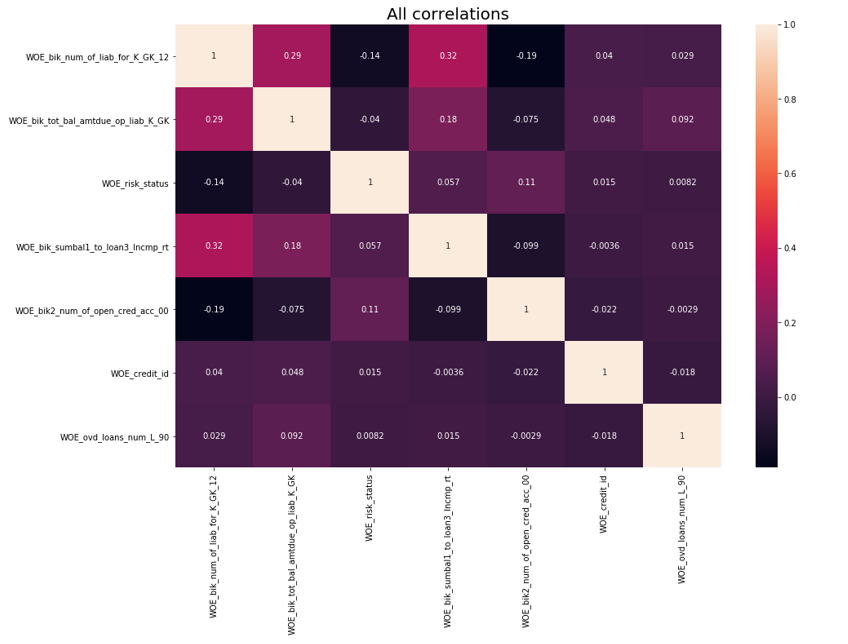
Korrelationsentfernung def delete_correlated_features(df, cut_off=0.75, exclude = []):
Zusätzlich zur Auswahl nach IV haben wir eine rekursive Suche nach der optimalen Anzahl von Variablen nach der
RFE- Methode von sklearn hinzugefügt.
Wie wir in der Grafik sehen, ändert sich die Qualität nach 13 Variablen nicht, was bedeutet, dass die zusätzlichen gelöscht werden können. Bei der Regression werden mehr als 15 Variablen in der Bewertung als schlechte Form angesehen, die in den meisten Fällen mithilfe von RFE korrigiert wird.
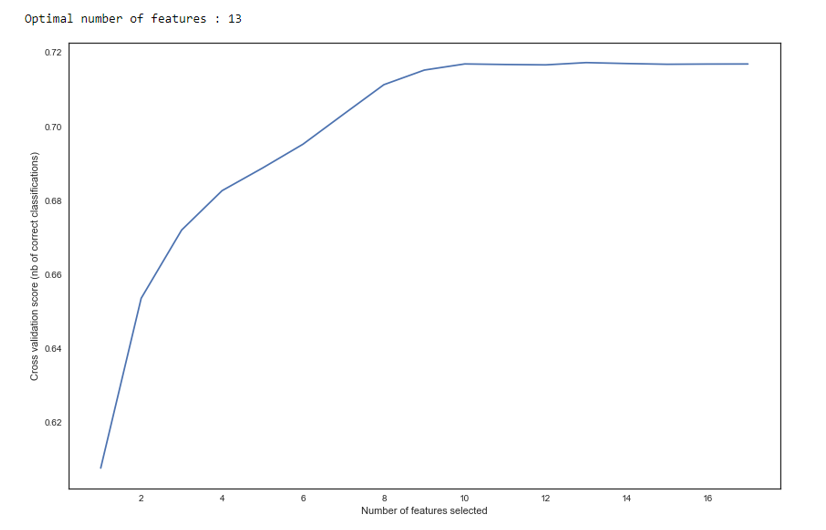
RFE def RFE_feature_selection(clf_lr, X, y): rfecv = RFECV(estimator=clf_lr, step=1, cv=StratifiedKFold(5), verbose=0, scoring='roc_auc') rfecv.fit(X, y) print("Optimal number of features : %d" % rfecv.n_features_)
Als nächstes wurde eine Regression erstellt und ihre Metriken wurden anhand von Kreuzvalidierung und Teststichproben bewertet. Normalerweise schaut sich jeder den Gini-Koeffizienten an (ein guter Artikel über ihn
hier ).
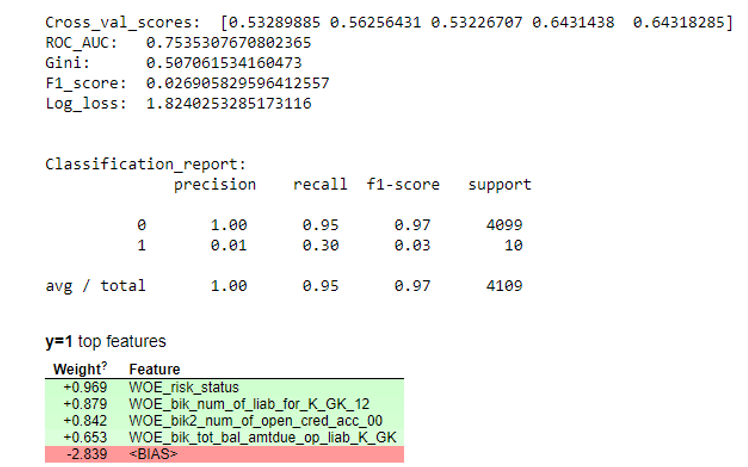
Simulationsergebnisse def plot_score(clf, X_test, y_test, feat_to_show=30, is_normalize=False, cut_off=0.5):
Wenn wir sicherstellen, dass die Modellqualität zu uns passt, müssen alle Ergebnisse (Regressionskoeffizienten, Bin-Gruppen, Gini-Stabilitätsdiagramme und -Variablen usw.) in Excel geschrieben werden. Zu diesem Zweck ist es zweckmäßig, xlsxwriter zu verwenden, der sowohl mit Daten als auch mit Bildern arbeiten kann.
Beispiele für Excel-Tabellen:
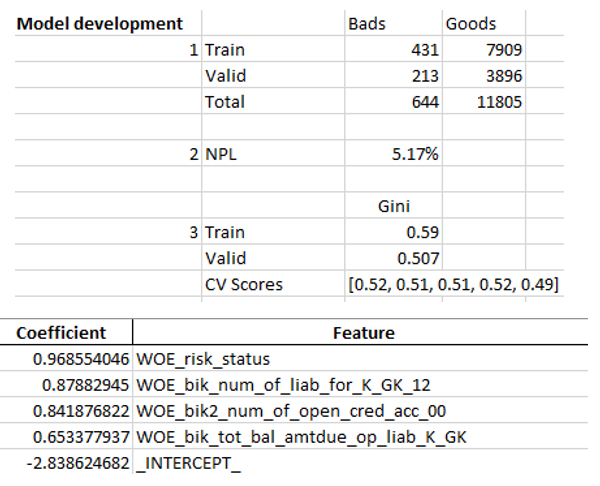
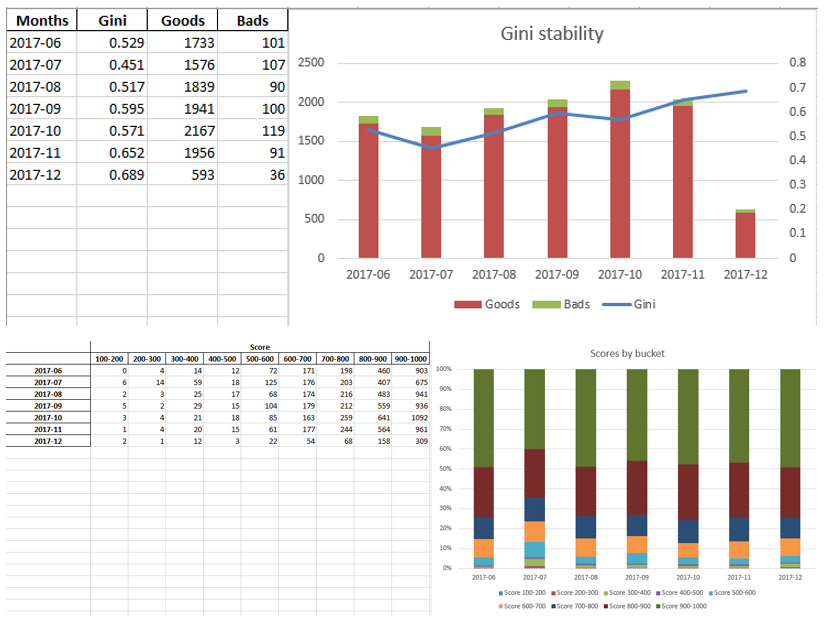
Am Ende wird das endgültige Excel erneut vom Management geprüft. Anschließend wird es der IT zur Einbettung des Modells in die Produktion übergeben.
Zusammenfassung
Wie wir gesehen haben, können fast alle Phasen des Scorings automatisiert werden, sodass Analysten keine Programmierkenntnisse benötigen, um Modelle zu erstellen. In unserem Fall muss der Analyst nach dem Erstellen dieses Frameworks nur Daten erfassen und mehrere Parameter angeben (geben Sie die Zielvariable an, welche Spalten entfernt werden sollen, die Mindestanzahl von Bins, den Grenzkoeffizienten für die Korrelation von Variablen usw.). Danach können Sie das Skript in Python ausführen. Dadurch wird das Modell erstellt und Excel mit den gewünschten Ergebnissen erstellt.
Natürlich ist es manchmal erforderlich, den Code für die Anforderungen eines bestimmten Projekts zu korrigieren, und Sie können das Skript während der Modellierung nicht mit einer einzigen Schaltfläche ausführen, aber selbst jetzt sehen wir dank Techniken wie optimalem und monotonem Binning und Korrelationsprüfung eine bessere Qualität als die auf dem Markt verwendeten Data Mining-Pakete , RFE, regulierte Version der Regression usw.
Dank der Verwendung von Python konnten wir die Entwicklungszeit für das Scoring von Karten erheblich reduzieren und die Arbeitskosten für Analysten senken.