Wie der geometrische 3D-Kern bei der Entwicklung von CAD-Anwendungen verwendet wird, sagt Valery Golovanev, Analyst, Ingenieur und Programmierer, Anwendungsentwickler für KOMPAS-3D. Mit einer lyrischen Einführung und einem tiefen Eintauchen in die Welt der mechanischen Zahnräder.



Mein Ururgroßvater Efim Stepanovich (ein Pflüger, ein Küfer und ein Zimmermann), mein Urgroßvater Trifon Efimovich (ein Pflüger und ein Zimmermann) und mein Großvater Mikhail Trifonovich (ein Schmied, ein Zimmermann, ein Zimmermann, ein Küfer) waren Handwerker. Und ich bin ein erfahrener Mensch. Ingenieur und Hobbyschreiner.

Es ist schwierig für jeden Meister ... Es ist schwierig ohne interessante Aufgaben, es ist schwierig, wenn es nicht genügend Möglichkeiten für ihre Implementierung gibt. Im Charakter eines echten Handwerkers, vor sich zu stellen, manchmal wenig machbar, Aufgaben zu übernehmen und umzusetzen.

Als ich vor sechs Jahren, im Sommer 2012, zu meiner Idee zurückkehrte - der Bibliothek zum Entwerfen von Revolutionskörpern KOMPAS-Shaft (jetzt die Anwendung „Wellen und mechanische 3D-Zahnräder“ für KOMPAS-3D)), stellte ich auf dem Ausdruck meiner IP ein paar Tricks mit einem kreisförmigen Zahn dar . In diesem Moment träumte ich nur davon, dass ich sie eines Tages in 3D machen könnte - es war eher eine Art Symbol. Mit zunehmendem Alter werden die Zeichen und Symbole des Schicksals sorgfältiger aufgenommen ... Das Ziel wurde verwirklicht!

Vom Schneckenrad zur Hypoidübertragung in KOMPAS-3D

Wie hat alles angefangen? Mit Verlangen! Ich wollte dem Designer unbedingt echte 3D-Modelle mechanischer Zahnräder und keine „Ähnlichkeiten“ geben, damit Sie:

1. Um ein Zahnrad oder ein Schneckenrad oder ein Sternchen gemäß dem 3D-Modell herzustellen. Oder ein kleiner Kegel mit einem kreisförmigen Zahn oder (über Träume ...) ein Hypoidpaar.
2. In der 3D-Baugruppe sind keine bedingten „Krokodile“ zu sehen, sondern echte Modelle.
3. Und weiter ... Und warum ist es eigentlich notwendig, sich bei mechanischen Getrieben auf die Möglichkeiten (Grenzen) konventioneller Technologie zu konzentrieren? Es ist falsch, das Design mit Technologie zu verletzen. Aus betrieblicher Sicht ist es notwendig, die richtigen Zahnräder mit der optimalen 3D-Geometrie der aktiven Arbeitsflächen herzustellen, und die Technologie sollte deren Herstellung sicherstellen. Und eine solche Technologie, Additiv genannt, gibt es bereits! Moderne industrielle 3D-Drucker ermöglichen es, vollständig beladene Produkte mit Metall zu bedrucken, und Experimente gehen weit: Teile, die mit der additiven Methode hergestellt wurden, werden in einem Maschinenbauprodukt bald alltäglich sein, wenn nicht in Massen, dann in kleinem Maßstab - ganz sicher.

Es hat ungefähr drei Jahre gedauert und im Frühjahr 2015 habe ich beschlossen, ein echtes Schneckenrad mit der COMPASS-API herzustellen. Das Implementierungsprinzip bei dieser Aufgabe war mir lange klar: Es ist notwendig, den Werkstückkörper mit einem Werkzeug zu fegen, dh die Bearbeitung in KOMPAS-3D zu simulieren. Um nicht zu sagen, dass es einfach war. Das Erstellen eines Ausschnitts mit einer Reihe zahlreicher Werkzeugpositionen ist falsch und lang. Es ist notwendig, eine Reihe von Flächen der Werkzeugpositionen zu bilden und eine Hüllfläche des Schnitts entlang dieser zu erstellen. Was im Grunde passiert ist, aber es hat sehr langsam funktioniert.

Zusätzlich war es notwendig, dem Prozess Realismus hinzuzufügen, d. H. Die Toleranzen bei der Bildung der 3D-Geometrie zu berücksichtigen. Nachdem ich ein Problem gelöst hatte, wollte ich im Allgemeinen mehr - mehr Genauigkeit, Messungen des Schneckenradzahns und die Bildung von Führungslinien in den Zeichnungen mit dem Profil dieses Zahns (was ist, wenn die Werkzeugtechnologen Messschablonen erstellen möchten?). Übrigens wurden im selben Jahr im Werk Kazzinkmash zwei Paar Schneckenräder nach meinen Vorbildern hergestellt, die erfolgreich in Arbeitseinheiten eingebaut wurden und positive Rückmeldungen erhielten.





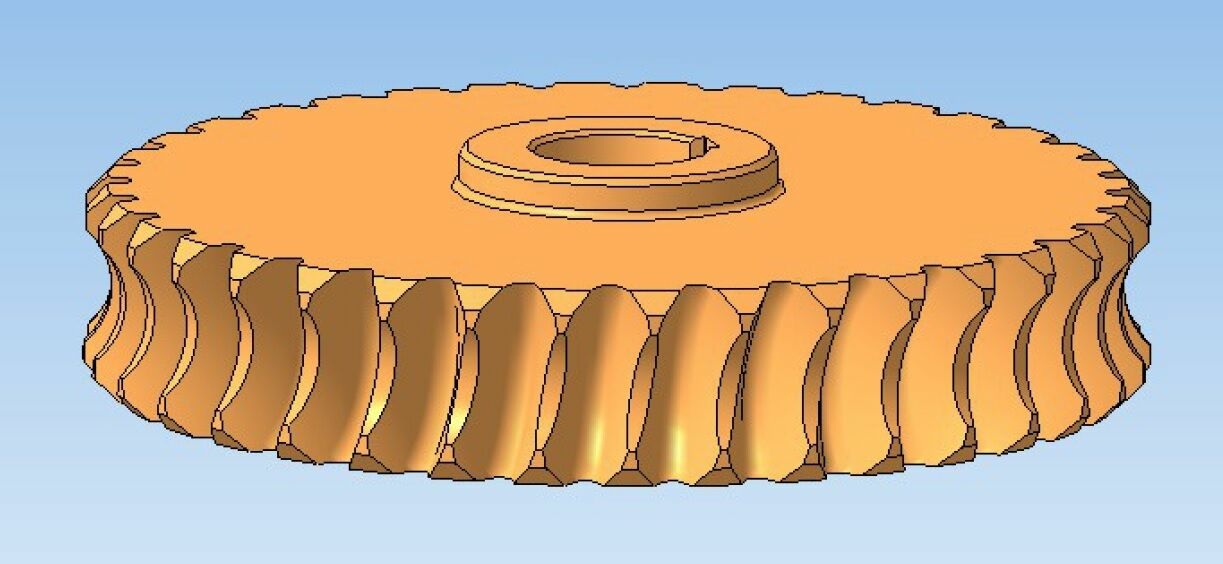
Mach weiter! Im Herbst 2015 begann ich mit der Einreichung (oder dem Kick) von Vladimir Panchenko, Leiter der Abteilung KOMPAS-3D-Anwendung, und unter der Anleitung von Alexei Sultanov, Programmierung auf dem C3D-Kern zu studieren, auf dessen Mathematik KOMPAS-3D aufgebaut ist. Das Ziel ist es, Freiheit zu bekommen! Und ich habe es verstanden. Ich war nicht länger durch die Anzahl der durchgeführten Operationen und Verfahren eingeschränkt. Alles ging schnell genug. Am Ausgang hatte ich eine Karosserie - eine Reihe von Ausschnitten aus dem Werkstück des Schneckenrads. Nun, dann ist alles einfach: Die Boolesche Operation und das Schneckenrad sind fertig.


Nikolay Golovanov, Leiter Entwicklung, C3D Labs

Einige Anwendungen des KOMPAS-3D-Systems, einschließlich der Anwendung „Wellen und mechanische Getriebe 3D“, arbeiten direkt mit dem geometrischen Kern C3D. Dies ermöglicht Anwendungsentwicklern einen flexibleren Ansatz zur Lösung ihrer Probleme, indem die Funktionalität (Arbeiten mit Funktionen auf niedriger Ebene) und Techniken zum Erstellen geometrischer Objekte erweitert werden.

Wenn Sie eine Anwendung für KOMPAS-3D schreiben und die Funktionen von C3D direkt nutzen möchten, ist es sinnvoll, auf den in KOMPAS-3D selbst integrierten Kernel zu verweisen. Diese Methode hat eine Einschränkung: Sie müssen nur C ++ verwenden, da COMPASS selbst in dieser Sprache geschrieben ist. Wenn Sie sich entscheiden, mit einer separaten Kopie des Kernels in Ihrer eigenen Anwendung zu arbeiten, stehen Ihnen C # und in einigen Fällen JavaScript zur Verfügung.

Es folgten Zylinder mit Außengetriebe. Es scheint einfach zu sein, aber im Fall eines Schrägverzahnungsgetriebes und eines Schraubenschnittvorgangs in KOMPAS-3D hat die Erstellung der API auch lange gedauert. Jetzt können diese Zahnräder mit einem echten Untergrund geformt werden.

Nun, Ende 2015 begann der Prozess der Arbeit an konischen Zähnen mit einem kreisförmigen Zahn.
Zu diesem Zeitpunkt wurde der Algorithmus auf der COMPASS-API ausgearbeitet. Die ersten Modelle mit nicht sehr guter Geometrie wurden vor einem Tag der reinen Zeit gebildet. Hier reichte eine Note der Oberflächen nicht aus. Es wurden Einlaufkegelräder hergestellt, und es war notwendig, ein Rad zu bilden, indem es mit einem Prototyp eines Zahnradschneidkopfes behandelt wurde. Formen und speichern Sie dann gemäß der erhaltenen 3D-Geometrie den Prototyp des Werkzeugs für das Zahnrad, entfernen Sie die kontrollierten Abmessungen von all dem und übertragen Sie ihn auf die Zeichnung. Ferner war es bereits am Zahnrad erforderlich, den Kontakt zu lokalisieren, d. H. Die richtige Position und Größe des Kontaktpunkts im Zahnrad sicherzustellen, da sich herausstellte, dass es perfekt eingefahren war.

Eine schwierige und sehr interessante Aufgabe. Gelegentlich haben Nikolai Golovanov und sein Team nach meinen Ausführungen die Funktionalität von C3D festgelegt. Somit waren meine kleinen Zapfen auch ein guter Test für den Kernel.


Nikolay Golovanov, Leiter Entwicklung, C3D Labs

In jüngster Zeit wurden im geometrischen Kern von C3D über Abschnitten aufgebaute Loft-Oberflächen einer erheblichen Verarbeitung unterzogen. Sie wurden verwendet, um die Kontaktpunkte der Zahnräder zu simulieren.

Konichki nach meinen Vorbildern wurden wiederholt in verschiedenen Unternehmen hergestellt und arbeiten in realen Knoten. Der Lokalisierungsalgorithmus wurde ausgearbeitet.



Aber es war schwierig, darüber nachzudenken. Eine solche Lokalisierung passte nicht zu mir. Es war zu schwierig zu liefern. Und im Frühjahr 2018 kam die Idee einer „einfacheren“ Lokalisierung. Eigentlich ist die Idee nicht meine, ich habe sie in den Materialien der Firma Klingelnberg ausspioniert - sie haben sie Profil und Längskrönung genannt .



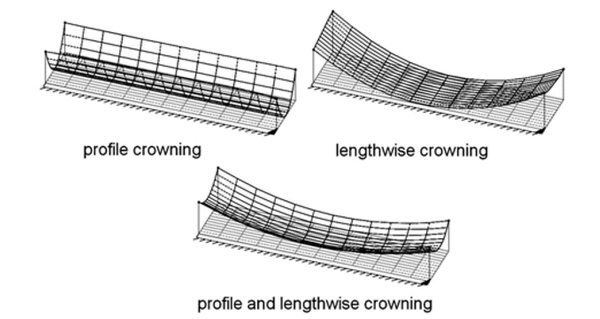
Ich nannte es "einen Zahn mit einem Hügel machen", was passierte. In jedem Abschnitt des Profils des Ausschnitts wurde seine Nachzählung durchgeführt, und der Hügel war ein Erfolg. Die Lokalisierungskoeffizienten sind einfacher und verständlicher geworden.



Kurz zum Ergebnis: Der Kontaktpunkt, und dies ist eine Reihe von Sofortkontaktflächen auf dem Zahnradzahn pro Zyklus seiner Drehung = 360 / Anzahl der Zahnradzähne, befindet sich JETZT IMMER in der Mitte der aktiven Oberfläche des Zahns (oben auf dem „Hügel“), seine Größe beträgt mehr als 60% die gesamte Oberfläche.

Was gibt es:

• Zahnräder werden langlebiger und zuverlässiger
• Das Übertragungsrauschen nimmt ab
• Das Getriebe reagiert weniger empfindlich auf Montagefehler.

Zwar wird es bisher möglich sein, sie nur auf CNC herzustellen, aber auch in Zukunft werden additive Technologien eingesetzt.

Nun, am Ende ... Dieses Jahr wurde die Traumübertragung verwirklicht, mein schwierigster Traum heute ist die Hypoidübertragung. Dafür musste viel getan werden ... Sechs Jahre nach der Rückkehr zur CAD-Entwicklung. Obwohl der Weg in der Realität bereits 1991 mit einem benutzerdefinierten Projekt zur Erstellung einer Software zur Berechnung von Kegelrädern mit einem kreisförmigen Zahn begann.



Natürlich ist der Zahnhügel in ihnen implementiert.




Vladimir Panchenko, Leiter der Anwendungsabteilung KOMPAS-3D, ASCON

Die Verwendung des Kerns in der Anwendung „Wellen und mechanische Getriebe“ wurde durch die Überprüfung von „Kazzinkmash“ veranlasst. Mir war klar, dass man schneller bauen kann. Alles, was übrig blieb, war, Valery davon zu überzeugen. Ein erschwerender Umstand war, dass Valery C ++ nicht mochte und Sie die C3D-Funktionen im Kontext von KOMPAS-3D nur in dieser Programmiersprache verwenden können. Dank Alexei Sultanov musste ich ein Layout erstellen.

Eine einfache Übersetzung des Codes in die Stirn führte sofort zu einem spürbaren Geschwindigkeitsgewinn: Das genaue Modell des Schneckenradzahns wurde in 10 Sekunden erstellt. Das Schneckenrad wurde ungefähr eine Stunde lang auf der API aufgebaut.

Nun, dann erlaubte Valerys Meisterschaft, einen Kegel mit einem kreisförmigen Zahn zu erzeugen.
Auf diese Weise haben wir das Projekt Wellen und mechanische Getriebe auf ein ganz neues Niveau gebracht.

Wie der 3D-Kern bei der Simulation mechanischer Zahnräder funktioniert

Die gebräuchlichsten Operationen werden aus der Kernelfunktionalität verwendet: Erstellen einer Ebene, Erstellen einer Skizze / Oberfläche / Schnittmenge von Oberflächen usw.

Betrachten Sie als Beispiel die Abfolge von Vorgängen, die erforderlich sind, um ein 3D-Modell eines Ausschnitts eines Kegelrads mit kreisförmigen Zähnen (nämlich Rädern, nicht Zahnrädern) zu erstellen:

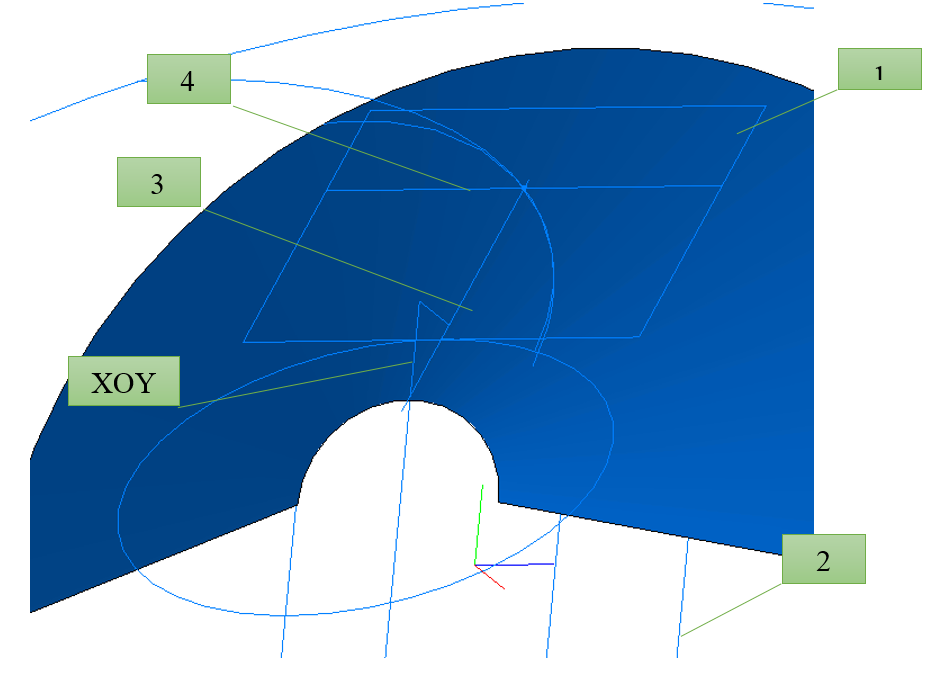
1. Wir bilden die Oberfläche der Kegel - den Teilungskegel, den Kegel der Gipfel und den Kegel der Tröge. Dazu werden Ebenen mit den entsprechenden berechneten Abständen erstellt und darauf Skizzen von Kreisen mit berechneten Durchmessern erstellt, auf denen bereits Kegel basieren.
2. Wir zeichnen die Punkte der Zentren des Trennkegels und des Kegels der Tröge.
3. Als nächstes werden eine Tangentialebene zum Kegel der Vertiefungen (1) und eine Ebene entlang des Mittelpunkts des Rades in der Vertiefung (2) gebildet. Am Schnittpunkt der Ebene (1) und der XOY-Ebene wird die Schnittachse (3) gebildet, und am Schnittpunkt der Ebene (2) und der Ebene (1) wird die Schnittachse (4) gebildet.
4. Am Schnittpunkt dieser Achsen befindet sich ein Punkt, durch den die Oberseite des Zahnradschneidkopfs verläuft.
   
   
   
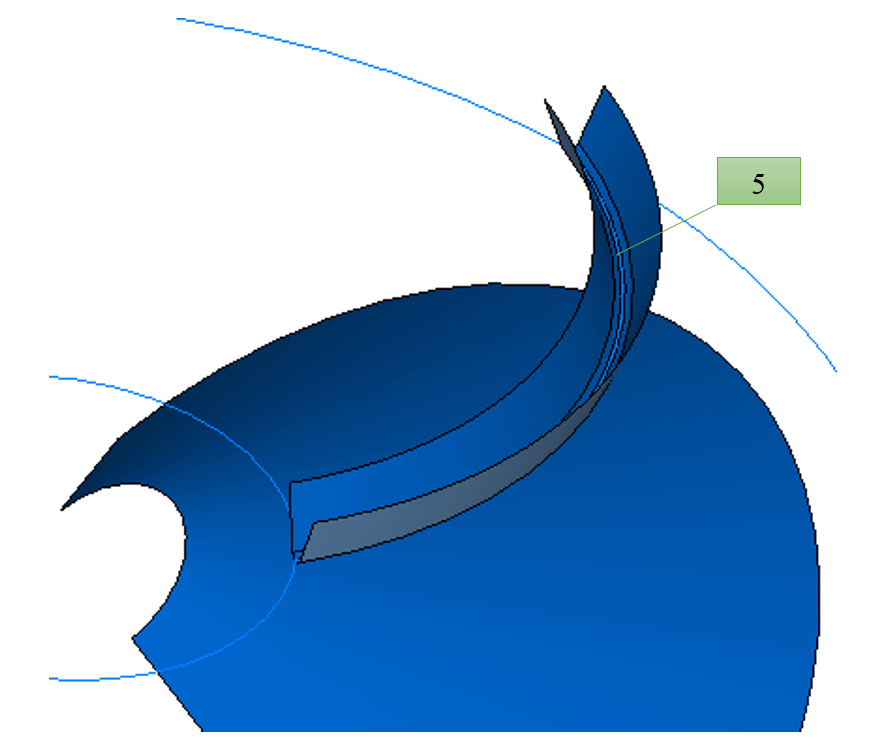
5. Ab diesem Punkt berechnen wir unter Kenntnis des durchschnittlichen Neigungswinkels der Zähne (genau an diesem Punkt) die Mitte des Zahnradschneidkopfs.
6. Die Vorsprünge des Halbbogens des Zahnradschneidkopfes auf die Kegel der Mulden (5) und den Trennkegel sind unsere Leitfäden. Auf dieser Führung (5) wird die Grundfläche der Aussparung aufgebaut (ein Dachboden in drei Abschnitten mit dem berechneten Profil des Zahnradschneidkopfes).
   
   
   
7. Wenn wir ein Verfahren zum Durchführen eines ähnlichen Vorgangs bei verschiedenen Drehwinkeln des Zahnradschneidkopfes bei der Bearbeitung des Rades haben, erhalten wir ferner eine Anordnung von Ausschnittflächen (6).
   
   
   
8. Danach werden in einer ausreichenden Anzahl von Abschnitten (mindestens 20) in normalen Ebenen zur Führung (der Projektion des Halbbogens des Zahnradschneidkopfes auf den Trennkegel) Sätze von Schnittlinien der Oberflächenanordnung erhalten.
   
   
   
9. Durch die mathematische Verarbeitung des resultierenden Satzes von Schnittlinien können Sie deren Hüllkurve erhalten, die einer der Abschnitte des tatsächlichen Ausschnitts des Zahns des Rads ist.
   
   
   
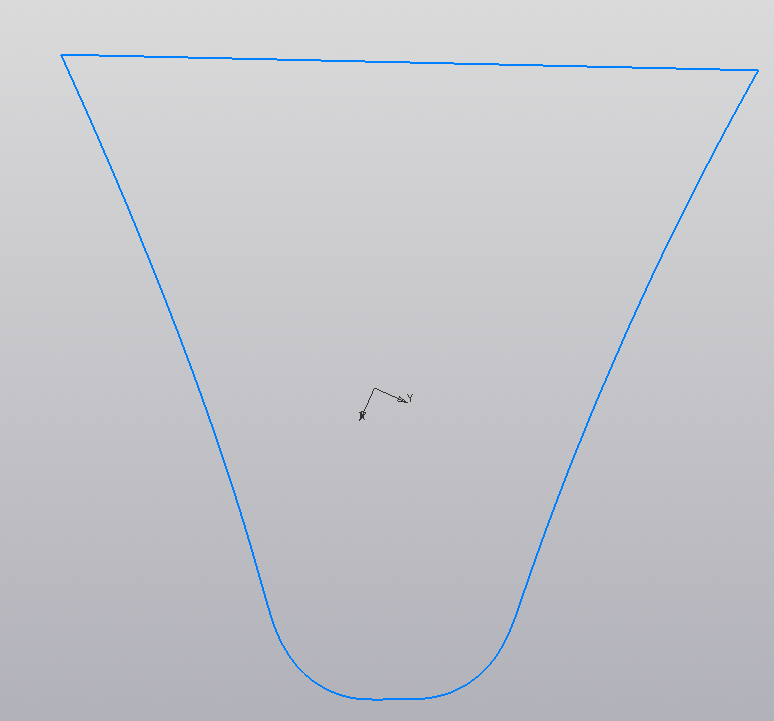
10. Basierend auf der Gesamtheit dieser Abschnitte der Ausschnitte wird der endgültige Dachboden gebaut - der Ausschnitt des Zahns des Rades.
    
    
    
    
    
    
    
11. Die Kontrollabmessungen, das Zahnprofil selbst und all dies, was in die Zeichnung übertragen wird, werden automatisch aus der erhaltenen Geometrie übernommen (ein Zahn wird gebaut, ein Abschnitt wird erstellt und ein Abschnitt wird entsprechend erstellt und berechnet).
    
    
    
    
    
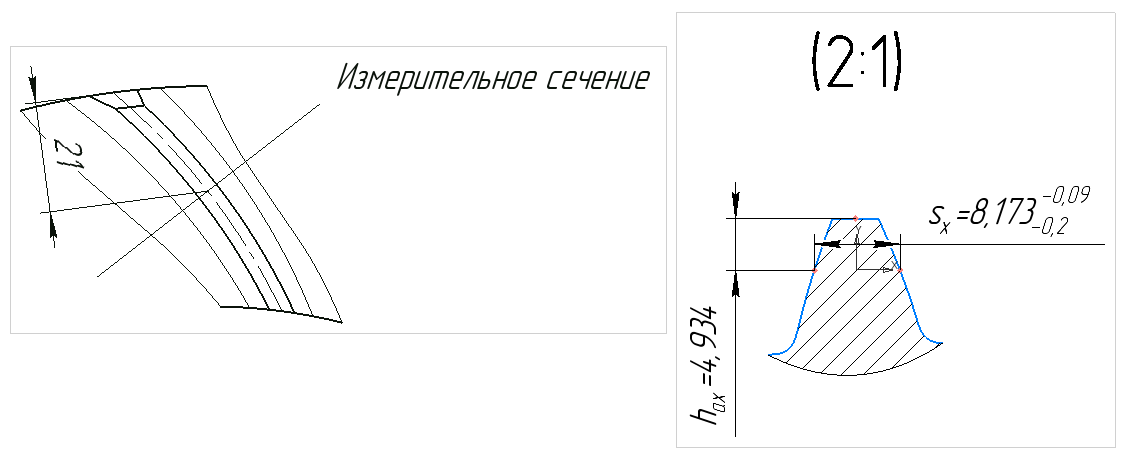
12. In diesem speziellen Fall ist jedoch alles recht einfach, ohne die „kleinen“ Nuancen mathematischer Berechnungen zu berücksichtigen, die den Lesern verborgen bleiben.

Was wird in diesem Fall noch für den Master benötigt? Raumphantasie, Fantasie und die Fähigkeit, am Ende zu träumen!


Vladimir Panchenko, Leiter der Anwendungsabteilung KOMPAS-3D, ASCON

Was ist schneller KOMPAS-3D oder C3D API? Die Frage klingt paradox. C3D ist der geometrische Kern von KOMPAS-3D! Wie der Kernel funktioniert, funktioniert auch COMPASS-3D. Bei näherer Betrachtung, insbesondere im Kontext des Anwendungsentwicklers, passt jedoch alles zusammen.

Das Standardschema für den Entwickler sieht so aus. Der Aufruf der KOMPAS-3D-API-Funktion führt zum Hinzufügen eines Objekts zum Dokumentmodell. Um dann die Geometrie zu erstellen, gehen wir zu C3D. Dann werden die Daten entlang der Kette in umgekehrter Reihenfolge an die API zurückgegeben und nun in den Händen des Entwicklers die Schnittstelle des erstellten Objekts.

Gleichzeitig passiert bei jedem Schritt etwas mit den Daten: In der API werden sie in COM gepackt, im Dokumentmodell auf Richtigkeit im aktuellen Kontext überprüft, Attribute und Zeichnungsdaten hinzugefügt. Natürlich sind alle diese Aktionen optimiert und nehmen sehr wenig Zeit in Anspruch. Wenn ein Entwickler eine zylindrische Wellenstufe benötigt, erstellt er in KOMPAS-3D eine Skizze und eine Extrusionsoperation - nur zwei Objekte und zwei Aufrufe entlang der Kette. Bei der Geometrie eines Kegelrads mit kreisförmigem Zahn ändert sich die Situation jedoch grundlegend. Dazu müssen Sie viele Hilfskurven, Flächen (und all dies sind keine analytischen Zylinder und Kegel, sondern NURBSs), deren Schnittpunkte, erstellen. Das Pumpen von Daten nimmt eine beträchtliche Zeit in Anspruch. Der Kern wird größtenteils im Leerlauf sein. Um Zeitverluste zu vermeiden, wird die Interaktion mit der API und dem Dokumentmodell minimiert. Fügen Sie eine Operation mit dem Body hinzu und nehmen Sie den Body, der in C3D modelliert ist. Wir erhalten einen Eintrag in C3D und erstellen optimalerweise auf dem Stapel die gesamte Hilfsgeometrie, schneiden die benötigten Elemente und erhalten das Ergebnis. Nur der Kernel funktioniert und arbeitet sehr schnell.

Valery Golovanev , Analyst und Programmierer, Kurgan, pos. Warmer Stan.