Ich hatte mit der Versuchung zu kämpfen, den Artikel so etwas wie "Die schreckliche Ineffizienz von STL-Algorithmen" zu nennen - wissen Sie, nur um die Kunst des Erstellens auffälliger Schlagzeilen zu trainieren. Trotzdem beschloss er, im Rahmen des Anstands zu bleiben - es ist besser, Kommentare von Lesern zum Inhalt des Artikels zu erhalten, als sich über seinen großen Namen zu empören.
An dieser Stelle gehe ich davon aus, dass Sie ein wenig mit C ++ und STL vertraut sind und sich auch um die in Ihrem Code verwendeten Algorithmen, deren Komplexität und Relevanz für die Aufgaben kümmern.
Algorithmen
Einer der bekannten Tipps, die Sie von der modernen C ++ - Entwicklergemeinde hören können, ist, keine Fahrräder zu entwickeln, sondern Algorithmen aus der Standardbibliothek zu verwenden. Das ist ein guter Rat. Diese Algorithmen sind sicher, schnell und wurden über die Jahre getestet. Ich gebe auch oft Ratschläge zur Anwendung.
Jedes Mal, wenn Sie ein anderes schreiben möchten, sollten Sie sich zuerst daran erinnern, ob die STL (oder der Boost) etwas enthält, das dieses Problem bereits in einer Zeile löst. Wenn ja, ist es oft besser, dies zu verwenden. In diesem Fall sollten wir jedoch auch verstehen, welche Art von Algorithmus hinter dem Aufruf der Standardfunktion steckt, welche Eigenschaften und Einschränkungen sie hat.
Wenn unser Problem genau mit der Beschreibung des Algorithmus von STL übereinstimmt, ist es normalerweise eine gute Idee, es zu nehmen und es „Stirn“ anzuwenden. Das einzige Problem ist, dass die Daten nicht immer in der Form gespeichert werden, in der der in der Standardbibliothek implementierte Algorithmus sie empfangen möchte. Dann haben wir vielleicht die Idee, zuerst die Daten zu konvertieren und dann immer noch denselben Algorithmus anzuwenden. Weißt du, wie in diesem Mathe-Witz: „Lösche das Feuer aus dem Kessel. Die Aufgabe ist auf die vorherige reduziert. “
Schnittmenge von Mengen
Stellen Sie sich vor, wir versuchen, ein Tool für C ++ - Programmierer zu schreiben, das alle Lambdas im Code mit der Erfassung aller Standardvariablen ([=] und [&]) findet und Tipps zur Konvertierung in Lambdas mit einer bestimmten Liste erfasster Variablen anzeigt. So etwas wie das:
std::partition(begin(elements), end(elements), [=] (auto element) {
Beim Parsen der Datei mit dem Code müssen wir die Sammlung von Variablen irgendwo im aktuellen und umgebenden Bereich speichern. Wenn bei der Erfassung aller Variablen ein Lambda erkannt wird, vergleichen Sie diese beiden Sammlungen und geben Sie Hinweise zu ihrer Konvertierung.
Ein Satz mit Variablen im übergeordneten Bereich und ein anderer mit Variablen im Lambda. Um Ratschläge zu erhalten, muss der Entwickler nur die Schnittstelle finden. Und dies ist der Fall, wenn die Beschreibung des Algorithmus von STL genau für die Aufgabe perfekt ist:
std :: set_intersection nimmt zwei Mengen und gibt ihre Schnittmenge zurück. Der Algorithmus ist in seiner Einfachheit schön. Es werden zwei sortierte Sammlungen verwendet und parallel durchlaufen:
- Wenn das aktuelle Element in der ersten Sammlung mit dem aktuellen Element in der zweiten identisch ist, fügen Sie es dem Ergebnis hinzu und fahren Sie mit den nächsten Elementen in beiden Sammlungen fort
- Wenn der aktuelle Artikel in der ersten Sammlung kleiner als der aktuelle Artikel in der zweiten Sammlung ist, fahren Sie mit dem nächsten Artikel in der ersten Sammlung fort
- Wenn das aktuelle Element in der ersten Sammlung größer als das aktuelle Element in der zweiten Sammlung ist, fahren Sie mit dem nächsten Element in der zweiten Sammlung fort
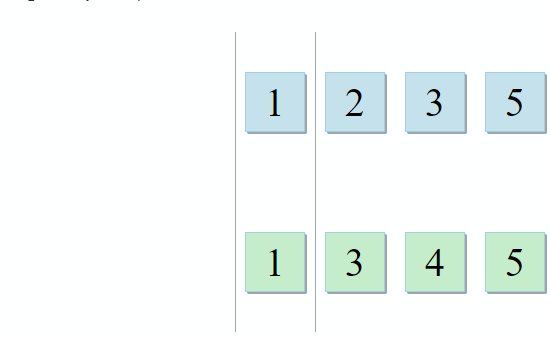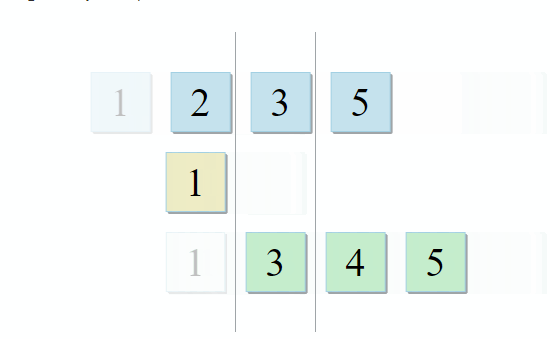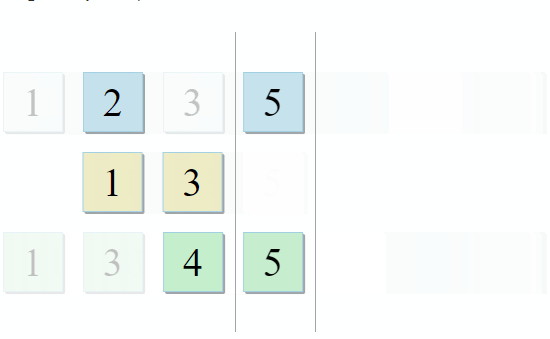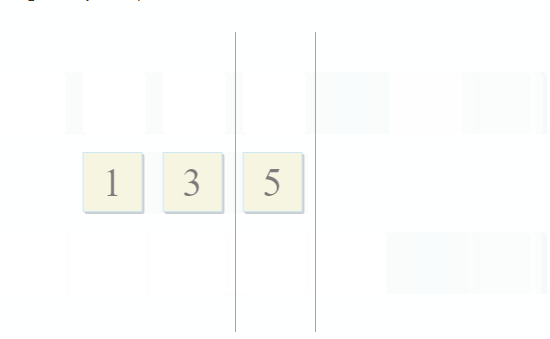
Mit jedem Schritt des Algorithmus bewegen wir uns entlang der ersten, zweiten oder beiden Sammlungen, was bedeutet, dass die Komplexität dieses Algorithmus linear ist - O (m + n), wobei n und m die Größen der Sammlungen sind.
Einfach und effektiv. Dies ist jedoch nur so weit, dass die Eingabesammlungen sortiert sind.
Sortieren
Das Problem ist, dass Sammlungen im Allgemeinen nicht sortiert sind. In unserem speziellen Fall ist es zweckmäßig, Variablen in einer Art stapelähnlicher Datenstruktur zu speichern, Variablen zur nächsten Stapelebene hinzuzufügen, wenn Sie einen verschachtelten Bereich betreten, und sie aus dem Stapel zu entfernen, wenn Sie diesen Bereich verlassen.
Dies bedeutet, dass die Variablen nicht nach Namen sortiert werden und wir std :: set_intersection nicht direkt für ihre Sammlungen verwenden können. Da std :: set_intersection genau sortierte Sammlungen an der Eingabe erfordert, kann die Idee entstehen (und ich habe diesen Ansatz in realen Projekten oft gesehen), Sammlungen zu sortieren, bevor die Bibliotheksfunktion aufgerufen wird.
Das Sortieren in diesem Fall wird die ganze Idee zunichte machen, einen Stapel zum Speichern von Variablen entsprechend ihrem Umfang zu verwenden, aber dennoch ist dies möglich:
template <typename InputIt1, typename InputIt2, typename OutputIt> auto unordered_intersection_1(InputIt1 first1, InputIt1 last1, InputIt2 first2, InputIt2 last2, OutputIt dest) { std::sort(first1, last1); std::sort(first2, last2); return std::set_intersection(first1, last1, first2, last2, dest); }
Was ist die Komplexität des resultierenden Algorithmus? So etwas wie O (n log n + m log m + n + m) ist quasilineare Komplexität.
Weniger sortieren
Können wir nicht sortieren? Wir können, warum nicht. Wir werden nur nach jedem Element aus der ersten Sammlung in der zweiten linearen Suche suchen. Wir erhalten die Komplexität O (n * m). Und diesen Ansatz habe ich auch in realen Projekten ziemlich oft gesehen.
Anstelle der Optionen "Alles sortieren" und "Nichts sortieren" können wir versuchen, Zen zu finden und den dritten Weg zu gehen - nur eine der Sammlungen sortieren. Wenn eine der Sammlungen sortiert ist, die zweite jedoch nicht, können wir die Elemente der unsortierten Sammlung einzeln durchlaufen und in der sortierten binären Suche nach ihnen suchen.
Die Komplexität dieses Algorithmus ist O (n log n) zum Sortieren der ersten Sammlung und O (m log n) zum Suchen und Überprüfen. Insgesamt erhalten wir die Komplexität O ((n + m) log n).
Wenn wir uns entscheiden, eine andere der Sammlungen zu sortieren, erhalten wir die Komplexität O ((n + m) log m). Wie Sie verstehen, wäre es logisch, hier eine kleinere Sammlung zu sortieren, um die endgültige Komplexität O ((m + n) log (min (m, n)) zu erhalten.
Die Implementierung sieht folgendermaßen aus:
template <typename InputIt1, typename InputIt2, typename OutputIt> auto unordered_intersection_2(InputIt1 first1, InputIt1 last1, InputIt2 first2, InputIt2 last2, OutputIt dest) { const auto size1 = std::distance(first1, last1); const auto size2 = std::distance(first2, last2); if (size1 > size2) { unordered_intersection_2(first2, last2, first1, last1, dest); return; } std::sort(first1, last1); return std::copy_if(first2, last2, dest, [&] (auto&& value) { return std::binary_search(first1, last1, FWD(value)); }); }
In unserem Beispiel mit Lambda-Funktionen und Erfassungsvariablen ist die Sammlung, die wir sortieren, normalerweise die Sammlung von Variablen, die im Code der Lambda-Funktion verwendet werden, da wahrscheinlich weniger Variablen als die Variablen im umgebenden Lambda-Bereich vorhanden sind.
Hashing
Die letzte in diesem Artikel beschriebene Option besteht darin, Hashing für eine kleinere Sammlung zu verwenden, anstatt sie zu sortieren. Dies gibt uns die Möglichkeit, darin nach O (1) zu suchen, obwohl die Konstruktion des Hash natürlich einige Zeit in Anspruch nehmen wird (von O (n) bis O (n * n), was zu einem Problem werden kann):
template <typename InputIt1, typename InputIt2, typename OutputIt> void unordered_intersection_3(InputIt1 first1, InputIt1 last1, InputIt2 first2, InputIt2 last2, OutputIt dest) { const auto size1 = std::distance(first1, last1); const auto size2 = std::distance(first2, last2); if (size1 > size2) { unordered_intersection_3(first2, last2, first1, last1, dest); return; } std::unordered_set<int> test_set(first1, last1); return std::copy_if(first2, last2, dest, [&] (auto&& value) { return test_set.count(FWD(value)); }); }
Der Hashing-Ansatz wird ein absoluter Gewinner sein, wenn unsere Aufgabe darin besteht, eine kleine Menge A konsistent mit einer Menge anderer (großer) Mengen B₁, B₂, B ... zu vergleichen. In diesem Fall müssen wir einen Hash für A nur einmal erstellen, und wir können seine sofortige Suche verwenden, um ihn mit den Elementen aller betrachteten Mengen B zu vergleichen.
Leistungstest
Es ist immer nützlich, die Theorie mit der Praxis zu bestätigen (insbesondere in Fällen wie dem letzteren, in denen nicht klar ist, ob sich die anfänglichen Kosten für das Hashing mit einem Gewinn an Suchleistung auszahlen).
In meinen Tests zeigte die erste Option (mit Sortierung beider Sammlungen) immer die schlechtesten Ergebnisse. Das Sortieren nur einer kleineren Sammlung funktionierte bei Sammlungen derselben Größe etwas besser, aber nicht zu viel. Der zweite und dritte Algorithmus zeigten jedoch eine sehr signifikante Produktivitätssteigerung (etwa sechsmal) in Fällen, in denen eine der Sammlungen 1000-mal größer war als die andere.