Wir setzen unseren Zyklus auf dem Monero-Blockchain-Gerät fort. Der heutige Artikel widmet sich dem RingCT-Protokoll (Ring Confidential Transactions), das vertrauliche Transaktionen und neue Ringsignaturen enthält. Leider gibt es im Internet nur wenige Informationen darüber, wie es funktioniert, und wir haben versucht, diese Lücke zu schließen.

Wir werden darüber sprechen, wie das Netzwerk die Anzahl der Übertragungen mithilfe dieses Protokolls verbirgt, warum wir die klassischen Ringsignaturen für Kryptonote abgelehnt haben und wie sich diese Technologie weiterentwickeln wird.
Da dieses Protokoll eine der komplexesten Technologien in Monero ist, benötigt der Leser Grundkenntnisse über das Gerät dieser Blockchain und oberflächliche Kenntnisse in der Kryptographie auf elliptischen Kurven (um dieses Wissen aufzufrischen, können Sie die ersten Kapitel unseres vorherigen Artikels über
Mehrfachsignaturen lesen).
RingCT-Protokoll
Einer der möglichen Angriffe auf Kryptonotenwährungen ist die Blockchain-Analyse, die auf der Kenntnis des Betrags und der Zeit der gesendeten Transaktion basiert. Es erlaubt
Die Suche nach den für den Angreifer interessanten Ergebnissen erheblich eingrenzen. Zum Schutz vor einer solchen Analyse hat Monero ein anonymes Transaktionsprotokoll eingeführt, das die Anzahl der Übertragungen im Netzwerk vollständig verbirgt.
Es ist erwähnenswert, dass die Idee, Beträge zu verstecken, nicht neu ist. Einer der ersten, der dies beschrieb, war der Bitcoin Core-Entwickler Greg Maxwell in seinem
Artikel über vertrauliche Transaktionen . Die aktuelle Implementierung von RingCT ist die Modifikation mit der Möglichkeit, Ringsignaturen (ohne diese) zu verwenden, und erhielt daher den Namen "Ring Confidential Transactions".
Unter anderem hilft das Protokoll dabei, Probleme beim Mischen von Staubausgaben zu beseitigen - Ausgaben für eine kleine Menge (normalerweise in Form von Änderungen aus Transaktionen), die mehr Probleme verursachten, als sie selbst kosten.
Im Januar 2017 fand das Monero Hard Fork-Netzwerk statt, das die optionale Verwendung vertraulicher Transaktionen ermöglichte. Und im September dieses Jahres wurden solche Transaktionen mit der Hardgabel der Version 6 die einzigen, die im Netzwerk zulässig waren.
RingCT verwendet mehrere Mechanismen gleichzeitig: mehrschichtige verknüpfbare spontane anonyme Gruppensignaturen (im Folgenden als MLSAG bezeichnet), Pedersen-Verpflichtungen und Bereichsnachweise (dieser Begriff hat keine etablierte Übersetzung ins Russische).
Das RingCT-Protokoll führt zwei Arten anonymer Transaktionen ein: einfache und vollständige. Die erste Brieftasche wird generiert, wenn eine Transaktion mehr als eine Eingabe verwendet, die zweite - in der entgegengesetzten Situation. Sie unterscheiden sich in der Validierung der Transaktionsbeträge und der von der MLSAG-Signatur signierten Daten (mehr dazu weiter unten). Darüber hinaus können Transaktionen des vollständigen Typs mit einer beliebigen Anzahl von Eingaben generiert werden, es gibt keinen grundsätzlichen Unterschied. Das Buch
„Zero to Monero“ zu diesem Thema besagt, dass die Entscheidung, vollständige Transaktionen auf eine Eingabe zu beschränken, in Eile getroffen wurde und sich in Zukunft möglicherweise ändern wird.
MLSAG-Unterschrift
Erinnern Sie sich an die signierten Eingaben einer Transaktion. Jede Transaktion gibt etwas Geld aus und generiert. Geldmittel werden durch die Erstellung von Transaktionsausgaben generiert (eine direkte Analogie sind Banknoten), und die Ausgabe, die eine Transaktion ausgibt (schließlich geben wir im wirklichen Leben Banknoten aus), wird zu einer Eingabe (sorgfältig ist es hier sehr leicht, verwirrt zu werden).
Der Eingang bezieht sich auf mehrere Ausgänge, gibt jedoch nur einen aus, wodurch ein "Rauchschutz" entsteht, der die Analyse der Übersetzungsgeschichte erschwert. Wenn eine Transaktion mehr als eine Eingabe hat, kann eine solche Struktur in Form einer Matrix dargestellt werden, in der Zeilen Eingaben und Spalten Knetausgaben sind. Um dem Netzwerk zu beweisen, dass die Transaktion ihre Ausgaben ausgibt (kennt ihre geheimen Schlüssel), werden die Eingaben mit einer Ringsignatur signiert. Eine solche Signatur gibt eine Garantie dafür, dass der Unterzeichner die geheimen Schlüssel aus allen Elementen einer der Spalten kannte.
Bei vertraulichen Transaktionen werden die klassischen Kryptonoten-Ringsignaturen nicht mehr verwendet. Sie wurden durch MLSAG ersetzt, eine Version der ähnlichen einschichtigen Ringsignaturen (LSAG) mit mehreren
Eingängen .
Sie werden als mehrschichtig bezeichnet, da sie mehrere Eingaben gleichzeitig signieren, von denen jede mit mehreren anderen gemischt ist, dh eine Matrix wird signiert, nicht eine Zeile. Wie wir später sehen werden, hilft dies, die Größe der Signatur zu sparen.
Schauen wir uns an, wie eine Ringsignatur gebildet wird, am Beispiel einer Transaktion, die 2 reale Ausgaben ausgibt und m - 1 zufällige aus der Blockchain zum Kneten verwendet. Bezeichnen Sie die öffentlichen Schlüssel der Ausgaben, als die wir ausgeben
und Schlüsselbilder für sie jeweils:
Somit erhalten wir eine
2 x m Matrix. Zunächst müssen wir die sogenannten Herausforderungen für jedes Ausgangspaar berechnen:
Wir beginnen die Berechnungen mit den Ausgaben, die wir mit ihren öffentlichen Schlüsseln ausgeben:
und Zufallszahlen
Als Ergebnis erhalten wir die Werte:
mit denen wir die Herausforderung berechnen
Das nächste Paar von Ausgängen (um leichter zu verstehen, wo wir ersetzen, haben wir diese Werte in verschiedenen Farben hervorgehoben). Alle folgenden Werte werden in einem Kreis gemäß den in der ersten Abbildung angegebenen Formeln berechnet. Die Herausforderung für ein Paar realer Ausgaben wird zuletzt berechnet.
Wie wir sehen können, werden in allen Spalten mit Ausnahme derjenigen, die die realen Ausgaben enthält, zufällig generierte Zahlen verwendet
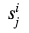
. Für die πte Spalte brauchen wir sie auch. Konvertieren
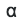
in s:
Die Signatur selbst ist ein Tupel all dieser Werte:
Ferner werden diese Daten in die Transaktion geschrieben.
Wie wir sehen können, enthält MLSAG nur eine Herausforderung
c 0 , wodurch die Größe der Signatur eingespart wird (die bereits viel Platz benötigt). Als nächstes jeder Prüfer, der die Daten verwendet
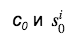
, stellt die Werte c
1 , ..., c
m wieder her und überprüft dies

. Somit wurde unser Ring geschlossen und die Unterschrift bestanden.
Bei RingCT-Transaktionen vom Typ full wird der Matrix eine weitere Zeile mit gemischten Ausgaben hinzugefügt. Wir werden jedoch weiter unten darauf eingehen.
Pedersen Verpflichtungen
Commitment-Schemata (häufig wird der englische Begriff verwendet - Commitments) werden verwendet, damit eine Seite nachweisen kann, dass sie ein bestimmtes Geheimnis (eine bestimmte Nummer) kennt, ohne es tatsächlich preiszugeben. Zum Beispiel werfen Sie eine bestimmte Zahl auf die Knochen, erwägen eine Verpflichtung und geben sie an die vertrauende Partei weiter. Zum Zeitpunkt der Enthüllung der Geheimnummer prüft der Inspektor die Verpflichtung unabhängig und stellt so sicher, dass Sie ihn nicht getäuscht haben.
Monero-Verpflichtungen werden verwendet, um die Anzahl der Überweisungen zu verbergen und die häufigste Option zu verwenden - Pedersen-Verpflichtungen. Übrigens eine merkwürdige Tatsache - zuerst schlugen die Entwickler vor, die Beträge mit dem üblichen Kneten zu verbergen, dh Ausgaben zu beliebigen Beträgen hinzuzufügen, um Unsicherheit zu verursachen, aber dann zu Verpflichtungen überzugehen (es ist keine Tatsache, dass sie bei der Größe der Transaktion gespart haben, wie wir weiter unten sehen werden).
Im Allgemeinen lautet das Engagement wie folgt:
Dabei ist
C der Wert der Verpflichtung selbst,
a der auszublendende Betrag,
H der feste Punkt auf der elliptischen Kurve (zusätzlicher Generator) und
x eine beliebige Maske, die den zufällig generierten Faktor verbirgt. Die Maske wird hier benötigt, damit der Dritte den Wert des Engagements nicht mit einer einfachen rohen Gewalt auswählen kann.
Beim Generieren eines neuen Exits berechnet die Brieftasche eine Verpflichtung dafür, und wenn sie ausgegeben wird, nimmt sie je nach Art der Transaktion entweder den während der Generierung berechneten Wert oder zählt ihn erneut.
Ringct einfach
Bei einfachen RingCT-Transaktionen sollten die Verpflichtungen der ersten und zweiten Transaktion gleich sein, um sicherzustellen, dass die Transaktion Outputs erzeugt, die der Summe der Inputs entsprechen (kein Geld aus der Luft verdient), dh:
Verpflichtungskommissionen betrachten etwas anders - ohne Maske:
Wenn
a die Höhe der Provision ist, ist sie öffentlich verfügbar.
Dieser Ansatz ermöglicht es uns, der vertrauenden Partei zu beweisen, dass wir dieselben Beträge verwenden, ohne sie preiszugeben.
Schauen wir uns zur Verdeutlichung ein Beispiel an. Angenommen, eine Transaktion gibt zwei Ausgaben (dh sie werden zu Eingaben) für 10 und 5 XMRs aus und generiert drei Ausgaben mit insgesamt 12 XMRs: 3, 4 und 5 XMRs. Gleichzeitig zahlt eine Provision von 3 XMR. Somit beträgt der ausgegebene Geldbetrag zuzüglich des generierten Betrags und der Provision 15 XMR. Versuchen wir, die Verpflichtungen zu berechnen und die Differenz in ihren Beträgen zu betrachten (denken Sie an die Mathematik):
Hier sehen wir, dass die Gleichung konvergiert - die Summen der Masken der Ein- und Ausgänge, die wir benötigen, sind gleich. Zu diesem Zweck generiert die Brieftasche zufällig
x 1 , y 1 , y 2 und y 3 , und das verbleibende
x 2 berechnet Folgendes:
Mit diesen Masken können wir jedem beweisen, der prüft, dass wir nicht mehr Geld generieren, als wir ausgeben, ohne den Betrag preiszugeben. Original, richtig?
RingCT voll
Bei vollständigen RingCT-Transaktionen ist die Überprüfung der Anzahl der Überweisungen etwas komplizierter. Bei diesen Transaktionen werden in der Brieftasche keine Verpflichtungen für Einträge nachgezählt, sondern diejenigen verwendet, die bei der Generierung berechnet wurden. In diesem Fall müssen wir davon ausgehen, dass die Differenz der Beträge nicht mehr gleich Null ist, sondern:
Hier ist
z der Unterschied zwischen den Masken der Ein- und Ausgänge. Wenn wir
zG als öffentlichen Schlüssel betrachten (was de facto der
Fall ist), dann ist
z ein privater Schlüssel. Somit kennen wir die öffentlichen und entsprechenden privaten Schlüssel. Mit diesen Daten können wir sie in der MLSAG-Ringsignatur zusammen mit den öffentlichen Schlüsseln der Knetausgaben verwenden:
Eine gültige Ringsignatur garantiert somit, dass wir alle privaten Schlüssel einer der Spalten kennen, und wir können den privaten Schlüssel in der letzten Zeile nur kennen, wenn die Transaktion nicht mehr Geld generiert, als sie ausgibt. Übrigens, hier ist die Antwort auf die Frage „Warum führt der Unterschied in der Höhe der Verpflichtungen nicht zu Null
? “ - wenn
zG = 0 ist , öffnen wir die Spalte mit den tatsächlichen Ergebnissen.
Aber woher weiß der Empfänger, wie viel Geld er ihm geschickt hat? Hier ist alles einfach - der Absender der Transaktion und der Empfänger tauschen Schlüssel mithilfe des Diffie-Hellman-Protokolls aus, verwenden den Transaktionsschlüssel und den Ansichtsschlüssel des Empfängers und berechnen das gemeinsame Geheimnis. Der Absender schreibt in die speziellen Felder der Transaktionsdaten die Summen der mit diesem gemeinsamen Schlüssel verschlüsselten Ausgaben.
Entfernungsnachweise
Aber was passiert, wenn Sie eine negative Zahl als Betrag für Verpflichtungen verwenden? Dies kann zur Erzeugung zusätzlicher Münzen führen! Ein solches Ergebnis ist inakzeptabel. Daher benötigen wir eine Garantie dafür, dass die von uns verwendeten Beträge nicht negativ sind (natürlich ohne Offenlegung dieser Beträge, sonst ist es so viel Arbeit und alles umsonst). Mit anderen Worten müssen wir beweisen, dass die Summe im Intervall
[0, 2 n - 1] liegt .
Hierzu wird die Summe jeder Ausgabe in Binärziffern unterteilt und die Verpflichtung für jede Ziffer separat betrachtet. Wie dies geschieht, ist es besser, ein Beispiel zu betrachten.
Angenommen, wir haben kleine Mengen und passen in 4 Bit (in der Praxis sind dies 64 Bit), und wir erstellen eine Ausgabe für die Menge von 5 XMR. Wir betrachten Verpflichtungen für jede Kategorie und eine allgemeine Verpflichtung für den gesamten Betrag:
Außerdem wird jede Verpflichtung mit einem Ersatz
(C i -2 i H) gemischt und paarweise mit der von Greg Maxwell im Jahr 2015 vorgeschlagenen Borromeo-Ringsignatur (eine weitere Ringsignatur) signiert (mehr dazu
hier ):
Zusammen wird dies als Bereichsnachweis bezeichnet und stellt sicher, dass Verpflichtungen Beträge im Intervall
[0, 2 n - 1] verwenden .
Was weiter?
In der aktuellen Implementierung nehmen Bereichsprüfungen viel Platz ein - 6176 Bytes pro Ausgabe. Dies führt zu großen Transaktionen und entsprechend höheren Provisionen. Um die Transaktionsgröße von Monero zu reduzieren, führen Entwickler anstelle von Borromeo-Signaturen Bulletproofs ein - einen entfernungssicheren Mechanismus ohne bitweise Verpflichtungen.
Nach einigen Schätzungen können sie die Reichweite der Proofgröße auf 94% reduzieren. Übrigens wurde die Technologie Mitte Juli von Kudelski Security
geprüft , wobei keine wesentlichen Mängel in der Technologie selbst oder in ihrer Implementierung festgestellt wurden. Die Technologie wird bereits im Testnetzwerk verwendet und kann mit der neuen harten Gabel wahrscheinlich in das Hauptnetzwerk verschoben werden.
Stellen Sie Ihre Fragen, schlagen Sie Themen für neue Artikel über Kryptowährungstechnologien vor und abonnieren Sie unsere Gruppe auf
Facebook , um über unsere Veranstaltungen und Veröffentlichungen auf dem Laufenden zu bleiben.