Geekly articles weekly

Nach Auswahl sortieren



Was ist die Idee, nach Wahl zu sortieren?

  1. In einem unsortierten Subarray wird ein lokales Maximum (Minimum) gesucht.
  2. Das gefundene Maximum (Minimum) ändert die Stellen mit dem letzten (ersten) Element im Subarray.
  3. Wenn unsortierte Subarrays im Array verbleiben, siehe Punkt 1.

Ein leichter lyrischer Exkurs. Zunächst wollte ich in meiner Artikelserie konsequent Material zu Sortierklassen in strenger Reihenfolge präsentieren. Nach der Sortierung der Bibliothek wurden Artikel über andere Einfügealgorithmen geplant: Solitairesortierung, Sortierung nach einer Young-Tabelle, Sortierung nach Inversion usw.

Jetzt ist der Trend jedoch Nichtlinearität. Daher werde ich heute, ohne alle Veröffentlichungen zum Sortieren nach Beilagen zu schreiben, einen parallelen Zweig zum Sortieren nach Auswahl starten. Dann mache ich dasselbe für andere algorithmische Klassen: Zusammenführungssortierungen, Verteilungssortierungen usw. Auf diese Weise können im Allgemeinen Veröffentlichungen zu einem Thema und dann zu einem anderen verfasst werden. Mit einer solchen thematischen Rotation wird es mehr Spaß machen.

Auswahl sortieren




Einfach und unprätentiös - wir gehen das Array auf der Suche nach dem maximalen Element durch. Das gefundene Maximum wird mit dem letzten Element ausgetauscht. Der unsortierte Teil des Arrays wurde um ein Element verringert (enthält nicht das letzte Element, in dem wir das gefundene Maximum neu angeordnet haben). Wir wenden die gleichen Aktionen auf diesen unsortierten Teil an - wir finden das Maximum und platzieren es an letzter Stelle im unsortierten Teil des Arrays. Und so fahren wir fort, bis der unsortierte Teil des Arrays auf ein Element reduziert ist.

def selection(data): for i, e in enumerate(data): mn = min(range(i, len(data)), key=data.__getitem__) data[i], data[mn] = data[mn], e return data


Das Sortieren mit einer einfachen Auswahl ist eine grobe Doppelsuche. Kann es verbessert werden? Schauen wir uns einige Modifikationen an.

Doppelte Auswahlsortierung :: Doppelte Auswahlsortierung




Eine ähnliche Idee wird bei der Shaker-Sortierung verwendet , bei der es sich um eine Variante der Blasensortierung handelt. Beim Durchlaufen des unsortierten Teils des Arrays finden wir neben dem Maximum auch gleichzeitig das Minimum. Wir setzen das Minimum an erster Stelle, das Maximum an letzter Stelle. Somit wird der unsortierte Teil bei jeder Iteration um zwei Elemente gleichzeitig reduziert.

Auf den ersten Blick scheint dies den Algorithmus um das Zweifache zu beschleunigen - nach jedem Durchgang wird das unsortierte Subarray nicht von einer, sondern von zwei Seiten gleichzeitig reduziert. Gleichzeitig stieg die Anzahl der Vergleiche um das Zweifache und die Anzahl der Swaps blieb unverändert. Die doppelte Auswahl erhöht die Geschwindigkeit des Algorithmus nur geringfügig und funktioniert in einigen Sprachen aus irgendeinem Grund sogar langsamer.

Der Unterschied zwischen der Sortierung nach Wahl und der Sortierung nach Einfügungen


Es scheint, dass das Sortieren nach Auswahl und das Sortieren nach Einfügungen ein und dasselbe ist, eine übliche Klasse von Algorithmen. Nun, oder das Sortieren nach Beilagen ist eine Art Sortieren nach Wahl. Oder das Sortieren nach Wahl ist ein Sonderfall beim Sortieren nach Beilagen. Und da und da wechseln wir uns vom unsortierten Teil des Arrays ab, um die Elemente zu extrahieren und in den sortierten Bereich umzuleiten.

Der Hauptunterschied: Beim Sortieren nach Einfügungen extrahieren wir jedes Element aus dem unsortierten Teil des Arrays und fügen es an seiner Stelle im sortierten Teil ein. Bei der Auswahlsortierung suchen wir gezielt nach dem maximalen Element (oder Minimum), mit dem wir den sortierten Teil des Arrays ergänzen. In den Einschüben suchen wir, wo das nächste Element eingefügt werden soll, und in der Auswahl - wir wissen bereits im Voraus, welchen Ort wir setzen werden, aber gleichzeitig müssen wir das Element finden, das diesem Ort entspricht.

Dies unterscheidet beide Klassen von Algorithmen in ihrem Wesen und den verwendeten Methoden völlig voneinander.

Bingo sort :: Bingo sort


Ein interessantes Merkmal der Sortierauswahl ist die Geschwindigkeitsunabhängigkeit der Art der zu sortierenden Daten.

Wenn das Array beispielsweise fast sortiert ist, wird es, wie Sie wissen, beim Sortieren nach Einfügungen viel schneller verarbeitet (sogar schneller als beim schnellen Sortieren). Ein Array in umgekehrter Reihenfolge zum Sortieren nach Einfügungen ist ein entarteter Fall. Es wird so lange wie möglich sortiert.

Und für die Sortierung nach Auswahl spielt die teilweise oder umgekehrte Reihenfolge des Arrays keine Rolle - es verarbeitet es ungefähr mit der gleichen Geschwindigkeit wie eine normale zufällige. Bei der klassischen Sortierung spielt es keine Rolle, ob das Array aus eindeutigen oder sich wiederholenden Elementen besteht - dies hat praktisch keinen Einfluss auf die Geschwindigkeit.

Im Prinzip können Sie den Algorithmus jedoch so konstruieren und modifizieren, dass er mit einigen Datensätzen schneller funktioniert. Bei der Bingo-Sortierung wird beispielsweise berücksichtigt, ob das Array aus sich wiederholenden Elementen besteht.



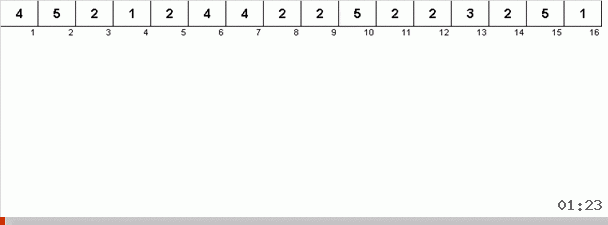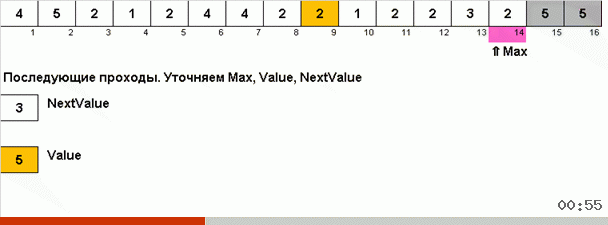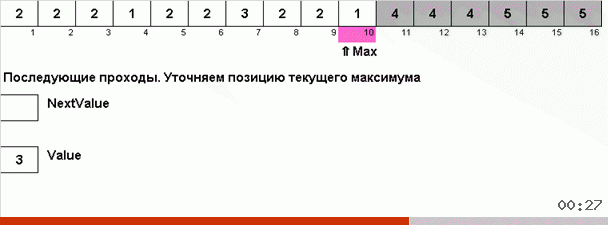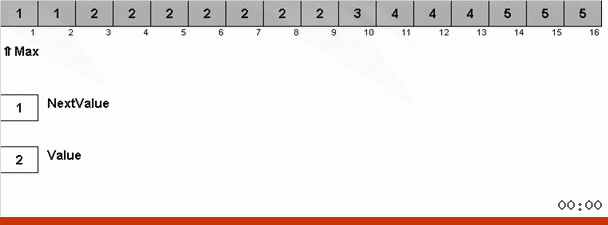
Der Trick dabei ist, dass nicht nur das maximale Element im ungeordneten Teil gespeichert wird, sondern auch das Maximum für die nächste Iteration bestimmt wird. Dies ermöglicht wiederholten Maxima, nicht jedes Mal erneut nach ihnen zu suchen, sondern sie an ihre Stelle zu setzen, sobald dieses Maximum erneut im Array angetroffen wird.

Die algorithmische Komplexität blieb gleich. Wenn das Array jedoch aus sich wiederholenden Zahlen besteht, ist die Bingo-Sortierung zehnmal schneller als die reguläre Sortierung nach Wahl.

 # - def bingo(data): #  . max = len(data) - 1 nextValue = data[max] for i in range(max - 1, -1, -1): if data[i] > nextValue: nextValue = data[i] while max and data[max] == nextValue: max -= 1 #  . while max: value = nextValue nextValue = data[max] for i in range(max - 1, -1, -1): if data[i] == value: data[i], data[max] = data[max], data[i] max -= 1 elif data[i] > nextValue: nextValue = data[i] while max and data[max] == nextValue: max -= 1 return data


Cycle sort :: Cycle sort


Die Schleifensortierung ist insofern interessant (und aus praktischer Sicht wertvoll), als Änderungen zwischen Array-Elementen genau dann auftreten, wenn das Element an seiner endgültigen Stelle platziert wird. Dies kann nützlich sein, wenn das Umschreiben in einem Array zu teuer ist und die Pflege des physischen Speichers die Minimierung der Anzahl der Änderungen an den Elementen des Arrays erfordert.



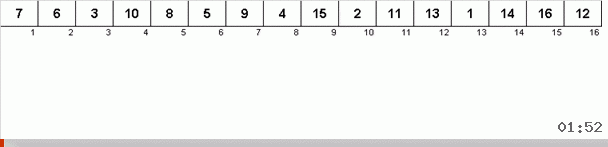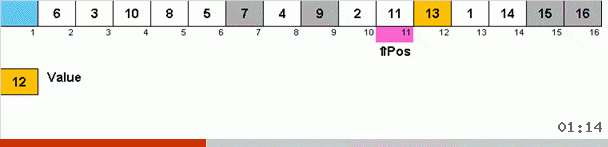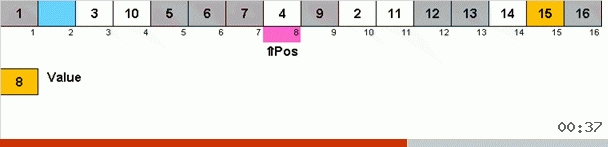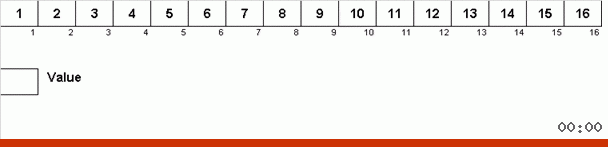
Es funktioniert so. Wir sortieren das Array und nennen X die nächste Zelle in dieser äußeren Schleife. Und wir schauen uns an, an welcher Stelle im Array wir das nächste Element aus dieser Zelle einfügen müssen. An der Stelle, an der Sie ein anderes Element einfügen möchten, senden wir es an die Zwischenablage. Für dieses Element im Puffer suchen wir auch nach seiner Position im Array (und fügen es an dieser Stelle ein und senden das an dieser Stelle angezeigte Element an den Puffer). Und für die neue Nummer im Puffer führen wir die gleichen Aktionen aus. Wie lange sollte dieser Prozess fortgesetzt werden? Bis sich herausstellt, dass das nächste Element in der Zwischenablage das Element ist, das genau in Zelle X eingefügt werden muss (die aktuelle Stelle im Array in der Hauptschleife des Algorithmus). Früher oder später wird dieser Moment eintreten und dann können Sie in der äußeren Schleife zur nächsten Zelle gehen und das gleiche Verfahren dafür wiederholen.

Bei anderen Arten suchen wir nach Wahl nach Maximum / Minimum, um sie an die letzte / erste Stelle zu setzen. Bei der Zyklus-Sortierung stellt sich heraus, dass sich mindestens der erste Platz im Subarray sozusagen in dem Prozess befindet, in dem mehrere andere Elemente irgendwo in der Mitte des Arrays an ihren richtigen Stellen platziert werden.

Und hier bleibt die algorithmische Komplexität auch innerhalb von O ( n 2 ). In der Praxis funktioniert die zyklische Sortierung sogar um ein Vielfaches langsamer als die reguläre Sortierung nach Wahl, da Sie das Array häufiger durchlaufen und häufiger vergleichen müssen. Dies ist der Preis für die kleinstmögliche Anzahl von Umschreibungen.

 #   def cycle(data): #        for cycleStart in range(0, len(data) - 1): value = data[cycleStart] # ,    pos = cycleStart for i in range(cycleStart + 1, len(data)): if data[i] < value: pos += 1 #      ,   #      if pos == cycleStart: continue #   ,     #        while value == data[pos]: pos += 1 data[pos], value = value, data[pos] #      , #         while pos != cycleStart: # ,    pos = cycleStart for i in range(cycleStart + 1, len(data)): if data[i] < value: pos += 1 #      #      while value == data[pos]: pos += 1 data[pos], value = value, data[pos] return data


Pfannkuchensortierung


Ein Algorithmus, der alle Ebenen des Lebens beherrscht - von Bakterien bis zu Bill Gates .



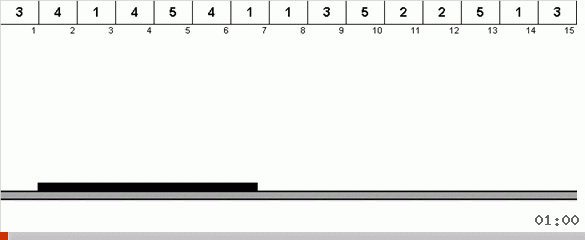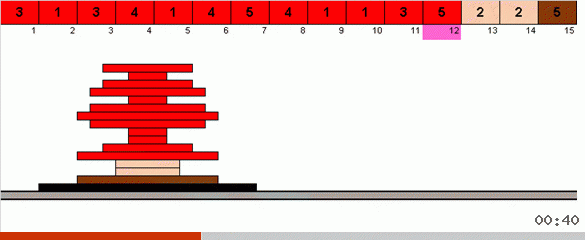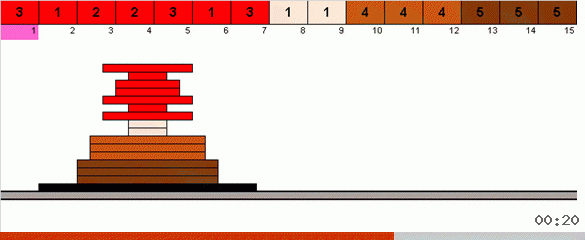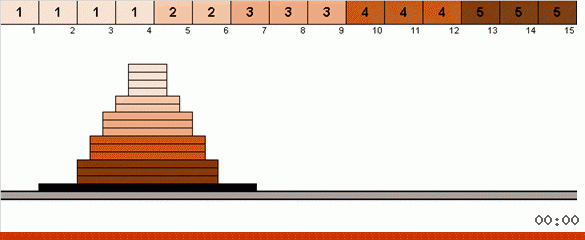
Im einfachsten Fall suchen wir nach dem maximalen Element im nicht sortierten Teil des Arrays. Wenn das Maximum gefunden ist, machen wir zwei scharfe Kurven. Zuerst drehen wir die Elementkette so, dass das Maximum am entgegengesetzten Ende liegt. Dann drehen wir das gesamte unsortierte Subarray um, wodurch das Maximum an seinen Platz fällt.

Solche Cordillets führen im Allgemeinen zu einer algorithmischen Komplexität in O ( n 3 ). Diese trainierten Ciliaten fallen auf einen Schlag (daher ist die Komplexität bei ihrer Ausführung O ( n 2 )), und beim Programmieren ist die Umkehrung eines Teils des Arrays ein zusätzlicher Zyklus.

Das Sortieren von Pfannkuchen ist aus mathematischer Sicht sehr interessant (die besten Köpfe haben darüber nachgedacht, die minimale Anzahl von Flips zu bewerten, die zum Sortieren ausreichen). Es gibt komplexere Formulierungen des Problems (wobei die sogenannte eine Seite ausgebrannt ist). Das Thema Pfannkuchen ist äußerst interessant. Vielleicht schreibe ich eine umfassendere Monographie zu diesen Themen.

 #   def pancake(data): if len(data) > 1: for size in range(len(data), 1, -1): #      maxindex = max(range(size), key = data.__getitem__) if maxindex + 1 != size: #    ,    if maxindex != 0: #  , #     data[:maxindex+1] = reversed(data[:maxindex+1]) #    , #      data[:size] = reversed(data[:size]) return data



Die Auswahlsortierung ist genauso effektiv wie die Suche nach dem minimalen / maximalen Element im unsortierten Teil des Arrays. Bei allen heute analysierten Algorithmen erfolgt die Suche in Form einer Doppelsuche. Und bei der Doppelsuche ist die algorithmische Komplexität, wie auch immer man sagen mag, immer nicht besser als O ( n 2 ). Bedeutet dies, dass alle Sortierungen nach Wahl dazu verdammt sind, quadratische Komplexität zu bedeuten? Überhaupt nicht, wenn der Suchprozess grundlegend anders organisiert ist. Betrachten Sie beispielsweise ein Dataset als Heap und suchen Sie auf dem Heap. Das Thema Haufen ist jedoch nicht einmal ein Artikel, sondern eine ganze Saga. Wir werden definitiv über Haufen sprechen, aber ein anderes Mal.

Referenzen


Auswahl / Zyklus , Pfannkuchen / Pfannkuchen

Serienartikel:



Das heutige Bingo, Fahrrad und Pfannkuchen wurden der AlgoLab-App hinzugefügt. In letzterem Fall wurde im Zusammenhang mit dem Zeichnen von Pfannkuchen eine Einschränkung festgelegt - die Werte der Elemente im Array sollten zwischen 1 und 5 liegen. Sie können natürlich mehr eingeben, aber die Makros nehmen zufällig Zahlen aus diesem Bereich.

Source: https://habr.com/ru/post/de422085/

More articles:


All Articles