Inwieweit ähneln die Daten für das Modelltraining (nicht) einer Testprobe?

Stellen Sie sich ein Szenario vor, in dem Ihr maschinelles Lernmodell möglicherweise wertlos ist.

Es gibt ein Sprichwort: "Vergleichen Sie Äpfel nicht mit Orangen . " Aber was ist, wenn Sie einen Satz Äpfel mit Orangen mit einem anderen vergleichen müssen, die Verteilung der Früchte in beiden Sätzen jedoch unterschiedlich ist? Können Sie mit Daten arbeiten? Und wie wirst du es machen?


In realen Fällen ist diese Situation häufig. Bei der Entwicklung von Modellen für maschinelles Lernen sehen wir uns mit einer Situation konfrontiert, in der unser Modell mit einem Trainingssatz gut funktioniert, die Qualität des Modells jedoch bei Testdaten stark abnimmt.

Und hier geht es nicht um Umschulung. Nehmen wir an, wir haben ein Modell erstellt, das bei der Kreuzvalidierung ein hervorragendes Ergebnis liefert, beim Test jedoch ein schlechtes Ergebnis zeigt. Im Testmuster gibt es also Informationen, die wir nicht berücksichtigen.

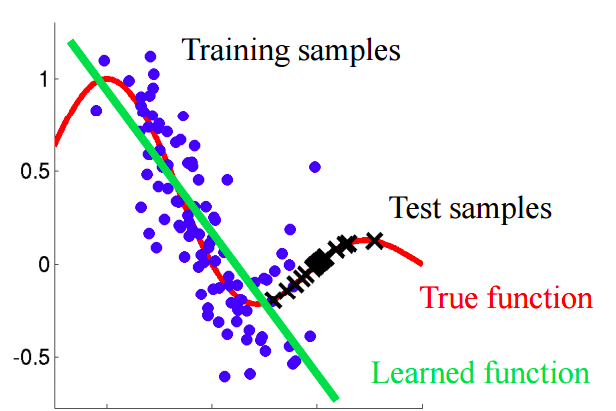
Stellen Sie sich eine Situation vor, in der wir das Kundenverhalten in einem Geschäft vorhersagen. Wenn die Trainings- und Testmuster wie im Bild unten aussehen, ist dies ein klares Problem:


In diesem Beispiel wird das Modell anhand von Daten trainiert, deren Durchschnittswert des Attributs "Kundenalter" niedriger ist als der Durchschnittswert eines ähnlichen Attributs im Test. Während des Lernprozesses hat das Modell die größeren Werte des Attributs "Alter" nie "gesehen". Wenn das Alter ein wichtiges Merkmal für das Modell ist, sollte man keine guten Ergebnisse für die Testprobe erwarten.

In diesem Text werden wir über „naive“ Ansätze sprechen, mit denen wir solche Phänomene identifizieren und versuchen können, sie zu beseitigen.

Kovariante Verschiebung

Lassen Sie uns dieses Konzept genauer definieren. Kovarianz bezieht sich auf die Werte der Merkmale, und Kovarianzverschiebung bezieht sich auf eine Situation, in der die Verteilung der Werte der Merkmale in den Trainings- und Testproben unterschiedliche Merkmale (Parameter) aufweist.

Bei realen Problemen mit einer großen Anzahl von Variablen ist die kovariante Verschiebung schwer zu erkennen. Der Artikel beschreibt die Methode zur Identifizierung sowie zur Berücksichtigung der kovarianten Verschiebung der Daten.

Hauptidee

Wenn sich die Daten verschieben, können wir beim Mischen der beiden Stichproben einen Klassifizierer erstellen, der bestimmen kann, ob das Objekt zu einer Trainings- oder Teststichprobe gehört.


Lassen Sie uns verstehen, warum dies so ist. Kehren wir zu dem Beispiel mit Kunden zurück, bei dem das Alter ein „verschobenes“ Zeichen für die Schulungs- und Testmuster war. Wenn wir einen Klassifikator (zum Beispiel basierend auf einem zufälligen Wald) nehmen und versuchen, die gemischte Stichprobe in Training und Test zu unterteilen, ist das Alter ein sehr wichtiges Zeichen für eine solche Klassifizierung.

Implementierung

Versuchen wir, die beschriebene Idee auf einen realen Datensatz anzuwenden. Verwenden Sie den Datensatz des Kaggle-Wettbewerbs.

Schritt 1: Datenaufbereitung

Zunächst folgen wir einer Reihe von Standardschritten: Reinigen, Lücken ausfüllen, Etikettencodierung für kategoriale Zeichen durchführen. Für das betreffende Dataset war kein Schritt erforderlich. Überspringen Sie daher die Beschreibung.

import pandas as pd #  train  test train = pd.read_csv('train.csv',low_memory=True) test = pd.read_csv('test.csv',low_memory=True) 

Schritt 2: Hinzufügen eines Datenquellenindikators

Es ist notwendig, beiden Teilen des Datensatzes einen neuen Indikator hinzuzufügen - Training und Test. Für das Trainingsmuster mit dem Wert "1" bzw. für den Test "0".

 #    ,   test,   train test['is_train'] = 0 train['is_train'] = 1 

Schritt 3: Kombinieren der Lern- und Testbeispiele

Jetzt müssen Sie die beiden Datensätze kombinieren. Da der Trainingsdatensatz eine Spalte mit den Zielwerten 'Ziel' enthält, die nicht im Testdatensatz enthalten ist, muss diese Spalte gelöscht werden.

 #  train, test df_combine = pd.concat([train, test], axis=0, ignore_index=True) #  target df_combine = df_combine.drop('target', axis =1) y = df_combine['is_train'].values #  x = df_combine.drop('is_train', axis=1).values #  tst, trn = test.values, train.values 

Schritt 4: Erstellen und Testen des Klassifikators

Für Klassifizierungszwecke verwenden wir den Random Forest Classifier, den wir konfigurieren, um die Beschriftungen der Datenquelle im kombinierten Datensatz vorherzusagen. Sie können jeden anderen Klassifikator verwenden.

 from sklearn.ensemble import RandomForestClassifier import numpy as np rfc = RandomForestClassifier(n_jobs=-1, max_depth=5, min_samples_leaf = 5) predictions = np.zeros(y.shape) #     

Wir verwenden eine geschichtete randomisierte Aufteilung von 4 Falten. Auf diese Weise behalten wir das Verhältnis der 'is_train'-Labels in jeder Falte wie in der ursprünglichen kombinierten Stichprobe bei. Für jede Partition trainieren wir den Klassifikator für den Großteil der Partition und sagen die Klassenbezeichnung für den kleineren zurückgestellten Teil voraus.

 from sklearn.model_selection import StratifiedKFold, cross_val_score skf = StratifiedKFold(n_splits=4, shuffle=True, random_state=100) for fold, (train_idx, test_idx) in enumerate(skf.split(x, y)): X_train, X_test = x[train_idx], x[test_idx] y_train, y_test = y[train_idx], y[test_idx] rfc.fit(X_train, y_train) probs = rfc.predict_proba(X_test)[:, 1] #   predictions[test_idx] = probs 

Schritt 5: Interpretieren Sie die Ergebnisse

Wir berechnen den Wert der ROC AUC-Metrik für unseren Klassifikator. Basierend auf diesem Wert schließen wir, wie gut unser Klassifikator eine kovariante Verschiebung der Daten zeigt.

Wenn der Klassifikator c die Objekte gut in die Trainings- und Testdatensätze unterteilt, sollte der Wert der ROC-AUC-Metrik deutlich größer als 0,5 sein, idealerweise nahe bei 1. Dieses Bild zeigt eine starke kovariante Verschiebung der Daten.

Finden Sie den Wert von ROC AUC:

 from sklearn.metrics import roc_auc_score print('ROC-AUC:', roc_auc_score(y_true=y, y_score=predictions)) # ROC-AUC: 0.49974692698385287 

Der resultierende Wert liegt nahe bei 0,5. Dies bedeutet, dass unser Qualitätsklassifizierer mit einem Zufallstag-Prädiktor identisch ist. Es gibt keine Hinweise auf eine kovariante Verschiebung der Daten.

Da der Datensatz von Kaggle stammt, ist das Ergebnis ziemlich vorhersehbar. Wie bei anderen Wettbewerben für maschinelles Lernen werden die Daten sorgfältig überprüft, um sicherzustellen, dass es keine Verschiebungen gibt.

Dieser Ansatz kann jedoch auch auf andere datenwissenschaftliche Probleme angewendet werden, um das Vorhandensein einer kovarianten Verschiebung kurz vor Beginn der Lösung zu überprüfen.

Weitere Schritte

Entweder beobachten wir eine kovariante Verschiebung oder nicht. Was tun, um die Qualität des Modells im Test zu verbessern?

1. Entfernen Sie voreingenommene Funktionen
2. Verwenden Sie Objektbedeutungsgewichte basierend auf Dichtekoeffizientenschätzungen

Entfernen voreingenommener Funktionen:

Hinweis: Die Methode ist anwendbar, wenn die Daten kovariant verschoben sind.

• Extrahieren Sie die Wichtigkeit von Attributen aus dem Random Forest Classifier, den wir zuvor erstellt und trainiert haben.
• Die wichtigsten Anzeichen sind genau diejenigen, die voreingenommen sind und eine Verschiebung der Daten verursachen.
• Beginnen Sie mit dem Wichtigsten, löschen Sie auf einer Basis, erstellen Sie das Zielmodell und überprüfen Sie dessen Qualität. Sammeln Sie alle Zeichen, bei denen die Qualität des Modells nicht abnimmt.
• Verwerfen Sie die gesammelten Merkmale aus den Daten und erstellen Sie das endgültige Modell.

Mit diesem Algorithmus können Sie Zeichen aus dem roten Korb im Diagramm entfernen.

Verwenden von Objektbedeutungsgewichten basierend auf Dichtekoeffizientenschätzungen

Hinweis: Die Methode ist unabhängig davon anwendbar, ob die Daten kovariant verschoben sind.

Schauen wir uns die Vorhersagen an, die wir im vorherigen Abschnitt erhalten haben. Für jedes Objekt enthält die Vorhersage die Wahrscheinlichkeit, dass dieses Objekt zum Trainingssatz für unseren Klassifikator gehört.

 predictions[:10] #array([0.39743827 ... 

Zum Beispiel glaubt unser Random Forest Classifier für das erste Objekt, dass es mit einer Wahrscheinlichkeit von 0,397 zum Trainingssatz gehört. Nennen Sie diesen Wert $$$P (Zug)$. Oder wir können sagen, dass die Wahrscheinlichkeit der Zugehörigkeit zu Testdaten 0,603 beträgt. Ebenso nennen wir Wahrscheinlichkeit $$$P (Test)$.

Nun ein kleiner Trick: Für jedes Objekt des Trainingsdatensatzes berechnen wir den Koeffizienten $$$w = \ frac {P (Test)} {P (Zug)}$.

Koeffizient $$$w$Gibt an, wie nahe ein Objekt aus dem Trainingssatz daran liegt, Daten zu testen. Die Hauptidee:

Wir können verwenden $$$w$wie Gewichte in einem der Modelle, um das Gewicht der Beobachtungen zu erhöhen, die der Testprobe ähnlich sehen. Intuitiv ist dies sinnvoll, da unser Modell datenorientierter sein wird als in einer Testsuite.

Diese Gewichte können mit dem Code berechnet werden:

 import seaborn as sns import matplotlib.pyplot as plt plt.figure(figsize=(20,10)) predictions_train = predictions[:len(trn)] weights = (1./predictions_train) - 1. weights /= np.mean(weights) #  plt.xlabel('  w') plt.ylabel(' ') sns.distplot(weights, kde=False) 

Die erhaltenen Koeffizienten können beispielsweise wie folgt auf das Modell übertragen werden:

 rfc = RandomForestClassifier(n_jobs=-1,max_depth=5) m.fit(X_train, y_train, sample_weight=weights) 

Ein paar Worte zum resultierenden Histogramm:

• Größere Gewichtswerte entsprechen Beobachtungen, die der Testprobe ähnlicher sind.
• Fast 70% der Objekte aus dem Trainingssatz haben ein Gewicht nahe 1 und befinden sich daher in einem Unterraum, der dem Trainingssatz und dem Testsatz gleichermaßen ähnlich ist. Dies entspricht dem zuvor berechneten AUC-Wert.

Fazit

Wir hoffen, dass dieser Beitrag Ihnen dabei hilft, die „kovariante Verschiebung“ der Daten zu identifizieren und zu bekämpfen.

Referenzen

[1] Shimodaira, H. (2000). Verbesserung der prädiktiven Inferenz unter kovariater Verschiebung durch Gewichtung der Log-Likelihood-Funktion. Journal of Statistical Planning and Inference, 90, 227-244.
[2] Bickel, S. et al. (2009). Diskriminatives Lernen unter Covariate Shift. Journal of Machine Learning Research, 10, 2137–2155
[3] github.com/erlendd/covariate-shift-adaption
[4] Link zum verwendeten Datensatz

PS Der Laptop mit dem Code aus dem Artikel kann hier angesehen werden .