Richard Hamming: Kapitel 13. Informationstheorie

Wir haben es geschafft!

"Ziel dieses Kurses ist es, Sie auf Ihre technische Zukunft vorzubereiten."

Hallo Habr. Erinnern Sie sich an den großartigen Artikel „Sie und Ihre Arbeit“ (+219, 2588 Lesezeichen, 429.000 Lesungen)?

Hamming (ja, ja, selbstüberprüfende und selbstkorrigierende Hamming-Codes ) hat ein ganzes Buch geschrieben, das auf seinen Vorlesungen basiert. Wir übersetzen es, weil der Mann geschäftlich spricht.

In diesem Buch geht es nicht nur um IT, sondern auch um den Denkstil unglaublich cooler Leute. „Dies ist nicht nur eine Anklage für positives Denken. Es beschreibt Bedingungen, die die Chancen erhöhen, gute Arbeit zu leisten. “

Vielen Dank für die Übersetzung an Andrei Pakhomov.

Die Informationstheorie wurde Ende der 1940er Jahre von C. E. Shannon entwickelt. Das Management von Bell Labs bestand darauf, dass er es "Kommunikationstheorie" nannte, weil Dies ist ein viel genauerer Name. Aus offensichtlichen Gründen hat der Name "Informationstheorie" einen wesentlich größeren Einfluss auf die Öffentlichkeit, daher hat Shannon ihn gewählt, und das wissen wir bis heute. Der Name selbst legt nahe, dass sich die Theorie mit Informationen befasst, was sie wichtig macht, da wir tiefer in das Informationszeitalter eindringen. In diesem Kapitel werde ich einige grundlegende Schlussfolgerungen aus dieser Theorie ansprechen. Ich werde einige der einzelnen Bestimmungen dieser Theorie nicht streng, sondern intuitiv belegen, damit Sie verstehen, was die "Informationstheorie" tatsächlich ist, wo Sie sie anwenden können und wo nicht .

Was ist „Information“? Shannon identifiziert Informationen mit Unsicherheit. Er wählte den negativen Logarithmus der Wahrscheinlichkeit eines Ereignisses als quantitatives Maß für die Informationen, die Sie erhalten, wenn ein Ereignis mit der Wahrscheinlichkeit p eintritt. Wenn ich Ihnen zum Beispiel sage, dass das Wetter in Los Angeles neblig ist, liegt p nahe bei 1, was uns im Großen und Ganzen nicht viele Informationen gibt. Aber wenn ich sage, dass es im Juni in Monterey regnet, dann wird diese Nachricht unsicher sein und mehr Informationen enthalten. Ein zuverlässiges Ereignis enthält keine Informationen, da log 1 = 0 ist.

Lassen Sie uns näher darauf eingehen. Shannon war der Ansicht, dass ein quantitatives Informationsmaß eine kontinuierliche Funktion der Wahrscheinlichkeit eines Ereignisses p sein sollte und für unabhängige Ereignisse additiv sein sollte - die Informationsmenge, die als Ergebnis zweier unabhängiger Ereignisse erhalten wird, sollte gleich der Informationsmenge sein, die als Ergebnis eines gemeinsamen Ereignisses erhalten wird. Beispielsweise wird das Ergebnis eines Würfel- und Münzwurfs normalerweise als eigenständiges Ereignis angesehen. Lassen Sie uns das Obige in die Sprache der Mathematik übersetzen. Wenn I (p) die Informationsmenge ist, die in dem Ereignis mit der Wahrscheinlichkeit p enthalten ist, dann erhalten wir für ein gemeinsames Ereignis, das aus zwei unabhängigen Ereignissen x mit der Wahrscheinlichkeit p ₁ und y mit der Wahrscheinlichkeit p _{2 besteht}


(x und y unabhängige Ereignisse)

Dies ist die funktionale Cauchy-Gleichung, die für alle p ₁ und p _{2 gilt} . Nehmen wir an, um diese Funktionsgleichung zu lösen

p ₁ = p ₂ = p,

es gibt



Wenn p ₁ = p ² und p ₂ = p, dann



usw. Wenn Sie diesen Prozess mit der Standardmethode für Exponentiale für alle rationalen Zahlen m / n erweitern, gilt Folgendes



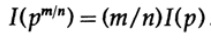
Aus der angenommenen Kontinuität des Informationsmaßes folgt, dass die logarithmische Funktion die einzige kontinuierliche Lösung für die funktionale Cauchy-Gleichung ist.

In der Informationstheorie ist es üblich, die Basis des Logarithmus von 2 zu verwenden, sodass die binäre Auswahl genau 1 Bit Information enthält. Daher werden Informationen durch die Formel gemessen



Lassen Sie uns innehalten und sehen, was oben passiert ist. Zunächst haben wir das Konzept der „Information“ nicht definiert, sondern lediglich eine Formel für das quantitative Maß definiert.

Zweitens hängt diese Maßnahme von der Unsicherheit ab, und obwohl sie für Maschinen - beispielsweise Telefonsysteme, Radio, Fernsehen, Computer usw. - ausreichend geeignet ist, spiegelt sie keine normale menschliche Einstellung zu Informationen wider.

Drittens ist dies ein relatives Maß, das vom aktuellen Wissensstand abhängt. Wenn Sie sich den Strom von „Zufallszahlen“ aus dem Zufallszahlengenerator ansehen, nehmen Sie an, dass jede nächste Zahl unbestimmt ist. Wenn Sie jedoch die Formel zur Berechnung von „Zufallszahlen“ kennen, ist die nächste Zahl bekannt und enthält dementsprechend keine Informationen.

Daher ist die von Shannon für Informationen gegebene Definition in vielen Fällen für Maschinen geeignet, scheint jedoch nicht dem menschlichen Verständnis des Wortes zu entsprechen. Aus diesem Grund sollte die „Informationstheorie“ als „Kommunikationstheorie“ bezeichnet werden. Es ist jedoch zu spät, um die Definitionen zu ändern (dank derer die Theorie ihre anfängliche Popularität erlangt hat und die Leute immer noch denken lassen, dass diese Theorie sich mit „Informationen“ befasst), also müssen wir uns mit ihnen abfinden, aber Sie müssen klar verstehen, inwieweit die von Shannon gegebene Definition von Informationen weit vom gesunden Menschenverstand entfernt ist. In Shannons Informationen geht es um etwas völlig anderes, nämlich um Unsicherheit.

Dies ist, woran Sie denken müssen, wenn Sie eine Terminologie anbieten. Wie konsistent ist die vorgeschlagene Definition, zum Beispiel die von Shannon gegebene Definition, mit Ihrer ursprünglichen Idee und wie unterschiedlich ist sie? Es gibt fast keinen Begriff, der Ihre frühere Vision des Konzepts genau widerspiegeln würde, aber letztendlich ist es die verwendete Terminologie, die die Bedeutung des Konzepts widerspiegelt, sodass die Formalisierung von etwas durch klare Definitionen immer etwas Lärm macht.

Stellen Sie sich ein System vor, dessen Alphabet aus Symbolen q mit den Wahrscheinlichkeiten pi besteht. In diesem Fall beträgt die durchschnittliche Informationsmenge im System (der erwartete Wert):



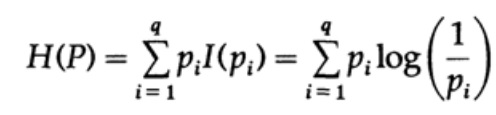
Dies nennt man die Entropie des Wahrscheinlichkeitsverteilungssystems {pi}. Wir verwenden den Begriff „Entropie“, weil in der Thermodynamik und der statistischen Mechanik dieselbe mathematische Form auftritt. Deshalb schafft der Begriff "Entropie" um sich herum eine Aura von Bedeutung, die letztendlich nicht gerechtfertigt ist. Dieselbe mathematische Form der Notation impliziert nicht dieselbe Interpretation von Zeichen!

Die Entropie der Wahrscheinlichkeitsverteilung spielt eine wichtige Rolle in der Codierungstheorie. Die Gibbs-Ungleichung für zwei verschiedene Wahrscheinlichkeitsverteilungen pi und qi ist eine der wichtigen Konsequenzen dieser Theorie. Das müssen wir also beweisen



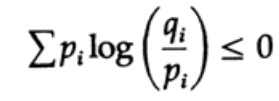
Der Beweis basiert auf einer offensichtlichen Grafik, Abb. 13.I, was das zeigt



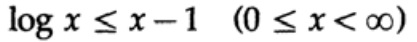
und Gleichheit wird nur für x = 1 erreicht. Wir wenden die Ungleichung auf jeden Summanden der Summe von der linken Seite an:



Wenn das Alphabet des Kommunikationssystems aus q Zeichen besteht, dann erhalten wir aus der Gibbs-Ungleichung die Wahrscheinlichkeit der Übertragung jedes Zeichens qi = 1 / q und ersetzen q





Abbildung 13.I.

Dies legt nahe, dass, wenn die Wahrscheinlichkeit der Übertragung aller q Zeichen gleich und gleich - 1 / q ist, die maximale Entropie ln q ist, andernfalls gilt die Ungleichung.

Im Fall eines eindeutig decodierten Codes haben wir die Kraft-Ungleichung



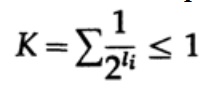
Nun definieren wir Pseudowahrscheinlichkeiten



wo natürlich = 1, was sich aus der Gibbs-Ungleichung ergibt,



und wenden Sie etwas Algebra an (denken Sie daran, dass K ≤ 1 ist, damit wir den logarithmischen Term weglassen und möglicherweise die Ungleichung später verstärken können)



Dabei ist L die durchschnittliche Länge des Codes.

Somit ist Entropie die minimale Grenze für jeden Zeichencode mit einem durchschnittlichen Codewort L. Dies ist Shannons Theorem für einen Kanal ohne Interferenz.

Wir betrachten nun den Hauptsatz zu den Einschränkungen von Kommunikationssystemen, in denen Informationen in Form eines Stroms unabhängiger Bits übertragen werden und Rauschen vorhanden ist. Es wird impliziert, dass die Wahrscheinlichkeit der korrekten Übertragung eines Bits P> 1/2 ist und die Wahrscheinlichkeit, dass der Bitwert während der Übertragung invertiert wird (ein Fehler tritt auf), Q = 1 - P ist. Der Einfachheit halber nehmen wir an, dass die Fehler unabhängig sind und die Fehlerwahrscheinlichkeit für jedes gesendete gleich ist Bits - das heißt, es gibt "weißes Rauschen" im Kommunikationskanal.

Die Art und Weise, wie ein langer Strom von n Bits in einer einzelnen Nachricht codiert ist, ist eine n-dimensionale Erweiterung eines Ein-Bit-Codes. Wir werden den Wert von n später bestimmen. Betrachten Sie eine Nachricht, die aus n-Bits besteht, als einen Punkt im n-dimensionalen Raum. Da wir einen n-dimensionalen Raum haben - und der Einfachheit halber nehmen wir an, dass jede Nachricht die gleiche Wahrscheinlichkeit des Auftretens hat - gibt es M mögliche Nachrichten (M wird auch später bestimmt), daher ist die Wahrscheinlichkeit einer gesendeten Nachricht gleich




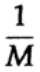
(Absender)
Grafik 13.II.

Betrachten Sie als nächstes die Idee der Kanalbandbreite. Ohne auf Details einzugehen, wird die Kanalkapazität als die maximale Informationsmenge definiert, die unter Berücksichtigung der Verwendung der effizientesten Codierung zuverlässig über den Kommunikationskanal übertragen werden kann. Es gibt kein Argument dafür, dass mehr Informationen über den Kommunikationskanal übertragen werden können als seine Kapazität. Dies kann für einen binären symmetrischen Kanal (den wir in unserem Fall verwenden) bewiesen werden. Die Kanalkapazität für das bitweise Senden ist auf eingestellt



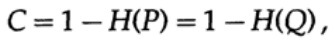
Dabei ist P wie zuvor die Wahrscheinlichkeit, dass in keinem gesendeten Bit ein Fehler auftritt. Beim Senden von n unabhängigen Bits wird die Kanalkapazität als bestimmt



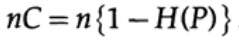
Wenn wir nahe an der Bandbreite des Kanals sind, sollten wir für jedes der Zeichen ai, i = 1, ..., M fast ein solches Informationsvolumen senden. Wenn die Wahrscheinlichkeit des Auftretens jedes Zeichens ai 1 / M beträgt, erhalten wir



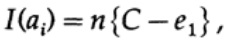
Wenn wir eine von M gleichwahrscheinlichen Nachrichten ai senden, haben wir



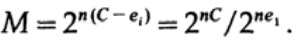
Beim Senden von n Bits erwarten wir, dass nQ-Fehler auftreten. In der Praxis haben wir für eine Nachricht, die aus n Bits besteht, ungefähr nQ Fehler in der empfangenen Nachricht. Für großes n relative Variation (Variation = Verteilungsbreite,)
Die Verteilung der Anzahl der Fehler wird mit zunehmendem n enger.

Von der Seite des Senders nehme ich die ai-Nachricht, um eine Kugel mit einem Radius um ihn herum zu senden und zu zeichnen



Dies ist um einen Betrag gleich e2 etwas größer als die erwartete Anzahl von Fehlern Q (Abbildung 13.II). Wenn n groß genug ist, besteht eine beliebig kleine Wahrscheinlichkeit für das Auftreten des Nachrichtenpunkts bj auf der Empfängerseite, die über diese Sphäre hinausgeht. Wir werden die Situation, wie ich sie aus Sicht des Senders sehe, zeichnen: Wir haben beliebige Radien von der gesendeten Nachricht ai zur empfangenen Nachricht bj mit einer Fehlerwahrscheinlichkeit, die gleich (oder fast gleich) der Normalverteilung ist und ein Maximum in nQ erreicht. Für jedes gegebene e2 ist n so groß, dass die Wahrscheinlichkeit, dass der resultierende Punkt bj, der über meine Sphäre hinausgeht, so klein ist, wie Sie möchten.

Betrachten Sie nun die gleiche Situation von Ihrer Seite (Abb. 13.III). Auf der Empfängerseite befindet sich eine Kugel S (r) mit dem gleichen Radius r um den empfangenen Punkt bj im n-dimensionalen Raum. Wenn sich die empfangene Nachricht bj in meiner Kugel befindet, befindet sich die von mir gesendete Nachricht ai in Ihrer Kugel.

Wie kann ein Fehler auftreten? In den in der folgenden Tabelle beschriebenen Fällen kann ein Fehler auftreten:



Abbildung 13.III



Hier sehen wir, dass, wenn in der Kugel, die um den empfangenen Punkt herum aufgebaut ist, mindestens ein weiterer Punkt vorhanden ist, der einer möglicherweise gesendeten nicht codierten Nachricht entspricht, während der Übertragung ein Fehler aufgetreten ist, da Sie nicht bestimmen können, welche dieser Nachrichten gesendet wurde. Die gesendete Nachricht enthält nur dann keine Fehler, wenn sich der entsprechende Punkt in der Kugel befindet und in diesem Code keine anderen Punkte möglich sind, die sich in derselben Kugel befinden.

Wir haben eine mathematische Gleichung für die Wahrscheinlichkeit eines Re-Fehlers, wenn ai gesendet wurde



Wir können den ersten Faktor im zweiten Term wegwerfen und ihn als 1 annehmen. So erhalten wir die Ungleichung



Offensichtlich



deshalb



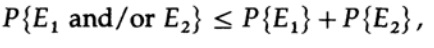
Wenden Sie sich erneut an das letzte Mitglied auf der rechten Seite



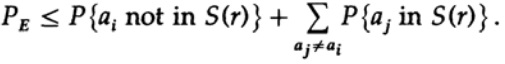
Wenn n groß genug genommen wird, kann der erste Term beliebig klein genommen werden, beispielsweise kleiner als eine bestimmte Zahl d. Deshalb haben wir



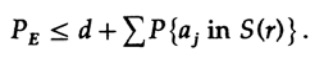
Nun wollen wir sehen, wie Sie einen einfachen Ersatzcode für die Codierung von M Nachrichten erstellen können, die aus n Bits bestehen. Da Shannon keine Ahnung hatte, wie der Code erstellt werden soll (Fehlerkorrekturcodes wurden noch nicht erfunden), entschied er sich für eine zufällige Codierung. Wirf eine Münze für jedes der n Bits in der Nachricht und wiederhole den Vorgang für M Nachrichten. Alles, was Sie tun müssen, ist daher nM Münzwurf



Code-Wörterbücher mit der gleichen Wahrscheinlichkeit von ½nM. Natürlich bedeutet der zufällige Prozess des Erstellens eines Codebuchs, dass die Wahrscheinlichkeit von Duplikaten sowie von Codepunkten besteht, die nahe beieinander liegen und daher eine Quelle für wahrscheinliche Fehler darstellen. Es muss bewiesen werden, dass das gegebene n groß genug ist, wenn dies nicht mit einer Wahrscheinlichkeit geschieht, die höher als eine kleine ausgewählte Fehlerstufe ist.
Der entscheidende Punkt ist, dass Shannon alle möglichen Codebücher gemittelt hat, um den durchschnittlichen Fehler zu finden! Wir werden das Av [.] Symbol verwenden, um den Durchschnitt über die Menge aller möglichen Zufallscode-Wörterbücher zu bezeichnen. Die Mittelung über die Konstante d ergibt natürlich eine Konstante, da zur Mittelung jeder Term mit jedem anderen Term in der Summe zusammenfällt



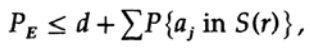
was erhöht werden kann (M - 1 geht an M)



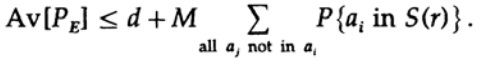
Bei einer bestimmten Nachricht durchläuft die Codierung bei der Mittelung aller Codebücher alle möglichen Werte. Die durchschnittliche Wahrscheinlichkeit, dass sich ein Punkt in einer Kugel befindet, ist also das Verhältnis des Volumens der Kugel zum Gesamtvolumen des Raums. Der Umfang der Kugel



Dabei ist s = Q + e2 <1/2 und ns muss eine ganze Zahl sein.

Der letzte Term rechts ist der größte in dieser Summe. Zunächst schätzen wir seinen Wert nach der Stirling-Formel für Fakultäten. Dann betrachten wir den Reduktionskoeffizienten des Termes davor, stellen fest, dass dieser Koeffizient zunimmt, wenn wir uns nach links bewegen, und daher können wir: (1) den Wert der Summe auf die Summe der geometrischen Progression mit diesem Anfangskoeffizienten begrenzen, (2) die geometrische Progression von ns Mitgliedern auf erweitern unendlich viele Terme, (3) berechne die Summe der unendlichen geometrischen Progression (Standardalgebra, nichts signifikantes) und erhalte schließlich den Grenzwert (für ein ausreichend großes n):



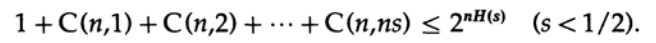
Beachten Sie, wie die Entropie H (s) in der Binomialidentität erschien. Es ist zu beachten, dass die Erweiterung in der Taylor-Reihe H (s) = H (Q + e2) eine Schätzung ergibt, die erhalten wird, indem nur die erste Ableitung berücksichtigt wird und alle anderen ignoriert werden. Sammeln wir nun den letzten Ausdruck:



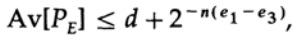
wo



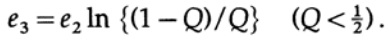
Alles was wir tun müssen, ist e2 so zu wählen, dass e3 <e1 ist, und dann wird der letzte Term beliebig klein sein, für n ausreichend groß. Daher kann der durchschnittliche PE-Fehler beliebig klein mit einer Kanalkapazität erhalten werden, die beliebig nahe bei C liegt.
Wenn der Durchschnitt aller Codes einen ausreichend kleinen Fehler aufweist, muss mindestens ein Code geeignet sein, daher existiert mindestens ein geeignetes Codierungssystem. Dies ist ein wichtiges Ergebnis von Shannon - „Shannons Theorem für einen Kanal mit Interferenz“, obwohl anzumerken ist, dass er es für einen viel allgemeineren Fall bewiesen hat als für einen einfachen binären symmetrischen Kanal, den ich verwendet habe. Für den allgemeinen Fall sind mathematische Berechnungen viel komplizierter, aber die Ideen sind nicht so unterschiedlich, so dass man sehr oft am Beispiel eines Sonderfalls die wahre Bedeutung des Satzes offenbaren kann.

Lassen Sie uns das Ergebnis kritisieren. Wir wiederholten wiederholt: "Für ausreichend große n." Aber wie groß ist n? Sehr, sehr groß, wenn Sie wirklich gleichzeitig nahe an der Bandbreite des Kanals sein und auf die richtige Datenübertragung achten möchten! So groß, dass Sie tatsächlich sehr lange warten müssen, um eine Nachricht aus so vielen Bits zu akkumulieren, um sie später zu codieren. In diesem Fall ist die Größe des Zufallscode-Wörterbuchs sehr groß (schließlich kann ein solches Wörterbuch nicht in einer kürzeren Form als die vollständige Liste aller Mn-Bits dargestellt werden, während n und M sehr groß sind)!

Fehlerkorrekturcodes vermeiden das Warten auf eine sehr lange Nachricht mit anschließender Codierung und Decodierung durch sehr große Codebücher, da sie Codebücher an sich vermeiden und stattdessen herkömmliche Berechnungen verwenden. In einer einfachen Theorie verlieren solche Codes in der Regel ihre Fähigkeit, sich der Kanalkapazität anzunähern und gleichzeitig eine relativ niedrige Fehlerrate beizubehalten. Wenn der Code jedoch eine große Anzahl von Fehlern korrigiert, zeigen sie gute Ergebnisse. Mit anderen Worten, wenn Sie eine Art Kanalkapazität für die Fehlerkorrektur festlegen, sollten Sie die Fehlerkorrekturoption die meiste Zeit verwenden, dh in jeder gesendeten Nachricht muss eine große Anzahl von Fehlern behoben werden, andernfalls verlieren Sie diese Kapazität vergeblich.

Darüber hinaus ist der oben bewiesene Satz immer noch nicht bedeutungslos! Es zeigt, dass effiziente Übertragungssysteme ausgefeilte Codierungsschemata für sehr lange Bitfolgen verwenden sollten. Ein Beispiel sind Satelliten, die außerhalb des äußeren Planeten geflogen sind. Wenn sie sich von der Erde und der Sonne entfernen, müssen sie immer mehr Fehler im Datenblock korrigieren: Einige Satelliten verwenden Solarbatterien, die ungefähr 5 Watt liefern, andere verwenden Atomstromquellen, die ungefähr die gleiche Leistung liefern.Die schwache Leistung der Stromquelle, die geringe Größe der Senderplatten und die begrenzte Größe der Empfängerplatten auf der Erde, die große Entfernung, die das Signal zurücklegen muss - all dies erfordert die Verwendung von Codes mit einem hohen Maß an Fehlerkorrektur, um ein effektives Kommunikationssystem aufzubauen.

Wir kehren zu dem n-dimensionalen Raum zurück, den wir im obigen Beweis verwendet haben. Als wir darüber diskutierten, zeigten wir, dass fast das gesamte Volumen der Kugel in der Nähe der Außenfläche konzentriert ist - daher befindet sich das gesendete Signal mit ziemlicher Sicherheit an der Oberfläche der Kugel, die um das empfangene Signal herum aufgebaut ist, selbst bei einem relativ kleinen Radius einer solchen Kugel. Daher ist es nicht überraschend, dass sich herausstellt, dass das empfangene Signal nach Korrektur einer beliebig großen Anzahl von Fehlern nQ dem Signal ohne Fehler beliebig nahe kommt. Die Kapazität des Kommunikationskanals, die wir zuvor untersucht haben, ist der Schlüssel zum Verständnis dieses Phänomens. Bitte beachten Sie, dass sich solche Kugeln, die für Hamming-Fehlerkorrekturcodes konstruiert wurden, nicht überlappen. Eine große Anzahl von praktisch orthogonalen Messungen im n-dimensionalen Raum zeigenWarum können wir M Kugeln in einen Raum mit einer leichten Überlappung einpassen? Wenn Sie eine kleine, willkürlich kleine Überlappung zulassen, die beim Decodieren nur zu einer geringen Anzahl von Fehlern führen kann, können Sie eine dichte Anordnung von Kugeln im Raum erhalten. Hamming garantierte ein gewisses Maß an Fehlerkorrektur, Shannon - eine geringe Fehlerwahrscheinlichkeit, hielt aber gleichzeitig die tatsächliche Bandbreite willkürlich nahe an der Kapazität des Kommunikationskanals, was Hamming-Codes nicht können.Gleichzeitig liegt die Aufrechterhaltung des tatsächlichen Durchsatzes willkürlich nahe an der Kapazität des Kommunikationskanals, was Hamming-Codes nicht können.Gleichzeitig liegt die Aufrechterhaltung des tatsächlichen Durchsatzes willkürlich nahe an der Kapazität des Kommunikationskanals, was Hamming-Codes nicht können.

Die Informationstheorie spricht nicht darüber, wie ein effektives System entworfen werden kann, sondern gibt die Bewegungsrichtung zu effektiven Kommunikationssystemen an. Dies ist ein wertvolles Werkzeug zum Aufbau von Kommunikationssystemen zwischen Maschinen, hat jedoch, wie bereits erwähnt, nicht viel damit zu tun, wie Menschen Informationen miteinander austauschen. Inwieweit die biologische Vererbung technischen Kommunikationssystemen ähnelt, ist einfach unbekannt. Daher ist derzeit nicht klar, wie die Informationstheorie auf Gene angewendet wird. Wir haben keine andere Wahl, als es zu versuchen, und wenn der Erfolg uns die maschinenähnliche Natur dieses Phänomens zeigt, wird das Scheitern auf andere wichtige Aspekte der Natur von Informationen hinweisen.

Lassen wir uns nicht viel ablenken. Wir haben gesehen, dass alle anfänglichen Definitionen mehr oder weniger das Wesen unserer anfänglichen Überzeugungen ausdrücken sollten, aber sie sind durch ein gewisses Maß an Verzerrung gekennzeichnet und daher nicht anwendbar. Es wird traditionell akzeptiert, dass letztendlich die Definition, die wir verwenden, tatsächlich das Wesen definiert; Aber es sagt uns nur, wie wir Dinge verarbeiten sollen und macht in keiner Weise Sinn. Der in mathematischen Kreisen so hoch gelobte postulative Ansatz lässt in der Praxis zu wünschen übrig.

Jetzt sehen wir uns ein Beispiel für IQ-Tests an, bei denen die Definition so zyklisch ist, wie Sie möchten, und Sie dadurch in die Irre führt. Es wird ein Test erstellt, der die Intelligenz messen soll. Danach wird überprüft, ob es so konsistent wie möglich ist, und dann wird es auf einfache Weise veröffentlicht und kalibriert, so dass die gemessene "Intelligenz" normal verteilt ist (natürlich entlang der Kalibrierungskurve). Alle Definitionen sollten überprüft werden, nicht nur wenn sie zum ersten Mal vorgeschlagen werden, sondern viel später, wenn sie in den Schlussfolgerungen verwendet werden. Inwieweit sind die Definitionsgrenzen für die jeweilige Aufgabe geeignet? Wie oft werden die unter denselben Bedingungen angegebenen Definitionen unter ganz unterschiedlichen Bedingungen angewendet? Das ist häufig genug!In den Geisteswissenschaften, denen Sie in Ihrem Leben unweigerlich begegnen werden, geschieht dies häufiger.

Daher bestand eines der Ziele dieser Präsentation der Informationstheorie neben dem Nachweis ihrer Nützlichkeit darin, Sie vor dieser Gefahr zu warnen oder zu demonstrieren, wie Sie sie verwenden können, um das gewünschte Ergebnis zu erzielen. Es ist seit langem bekannt, dass die anfänglichen Definitionen in viel größerem Maße bestimmen, was Sie am Ende finden, als es scheint. Erste Definitionen erfordern, dass Sie nicht nur in jeder neuen Situation, sondern auch in Bereichen, mit denen Sie lange gearbeitet haben, große Aufmerksamkeit schenken. Auf diese Weise können Sie nachvollziehen, inwieweit es sich bei den erzielten Ergebnissen um eine Tautologie handelt und nicht um etwas Nützliches.

, . , , , ! , .

...

, — magisterludi2016@yandex.ru

, — «The Dream Machine: » )

, , . ( 10 , 20 )