Verstecke dich ohne dich zu verstecken. Noch einmal über LSB-Steganographie, Chi-Quadrat und ... Singularität?

Heute werden wir wieder das alte Nest aufschlagen und darüber sprechen, wie man mit der Katze ein paar Teile im Bild versteckt, verschiedene verfügbare Werkzeuge ansieht und die beliebtesten Angriffe analysiert. Und es scheint, was hat die Singularität damit zu tun?

Wie sie sagen, wenn Sie etwas herausfinden wollen, dann schreiben Sie einen Artikel darüber auf Habr! (Achtung, viel Text und Bilder)



Steganographie (wörtlich aus der griechischen "Kryptographie") ist die Wissenschaft der Übertragung versteckter Daten (Stego-Nachrichten) in andere offene Daten (Stegocontainer), während die Tatsache der Datenübertragung verborgen bleibt. Seien Sie nicht beunruhigt, in der Tat ist nicht alles so kompliziert.

Wo im Bild können Sie die Nachricht verstecken, damit niemand es bemerkt?

Und es gibt nur zwei Stellen: Metadaten und das Bild selbst. Letzteres ist ganz einfach, geben Sie einfach "exif" bei Google ein. Beginnen wir also gleich mit dem zweiten.

Am wenigsten bedeutendes Stück

Das beliebteste Farbmodell ist RGB, bei dem die Farbe in Form von drei Komponenten dargestellt wird: Rot, Grün und Blau . Jede Komponente wird in der klassischen Version mit 8 Bit codiert, dh sie kann einen Wert von 0 annehmen
Hier verbirgt sich das niedrigstwertige Bit. Es ist wichtig zu verstehen, dass eine solche RGB-Farbe drei solcher Bits ausmacht.

Um sie klarer darzustellen, werden wir einige kleine Manipulationen vornehmen.

Machen Sie wie versprochen ein Foto von einer Katze im PNG-Format.



Wir teilen es in drei Kanäle auf und nehmen in jedem Kanal das niedrigstwertige Bit. Erstellen Sie drei neue Bilder, wobei jedes Pixel für NZB steht. Null - das Pixel ist weiß, die Einheit ist jeweils schwarz.

Wir bekommen das.




In der Regel befindet sich das Bild jedoch in der "zusammengesetzten Form". Um die NZB von drei Komponenten in einem Bild darzustellen, reicht es aus, die Komponente in einem Pixel zu ersetzen, in dem die NZB Eins ist, sie durch 255 zu ersetzen und sie ansonsten durch 0 zu ersetzen.

Aber nicht weniger bedeutsam

Stellen Sie sich vor, alles, was wir auf dem letzten Bild gesehen haben, gehört uns und wir haben das Recht, alles damit zu tun. Dann nehmen wir es als einen Strom von Bits, von wo aus wir lesen und wo wir schreiben können.

Wir nehmen die Daten, die wir in das Bild einstreuen möchten, präsentieren sie in Form von Bits und schreiben sie anstelle der vorhandenen auf.

Um diese Daten zu extrahieren, lesen wir die NZB als Bitstrom und bringen sie in die gewünschte Form. Um herauszufinden, wie viele Bits gezählt werden müssen, wird in der Regel die Nachrichtengröße an den Anfang geschrieben. Dies sind jedoch Implementierungsdetails.

Es ist zu beachten, dass in etwa 50% der Fälle das Bit, das wir schreiben möchten, und das Bit im Bild zusammenfallen und wir nichts ändern müssen.

Das ist alles, die Methode endet hier.

Warum funktioniert es?

Schauen Sie sich die Bilder unten an.

Dies ist ein leerer Stegocontainer:



Und das ist zu 95% voll:



Sehen Sie den Unterschied? Aber sie ist es. Warum so?

Schauen wir uns zwei Farben an: (0, 0, 0) und (1, 1, 1), dh Farben, die sich nur durch die NZB in jeder Komponente unterscheiden.



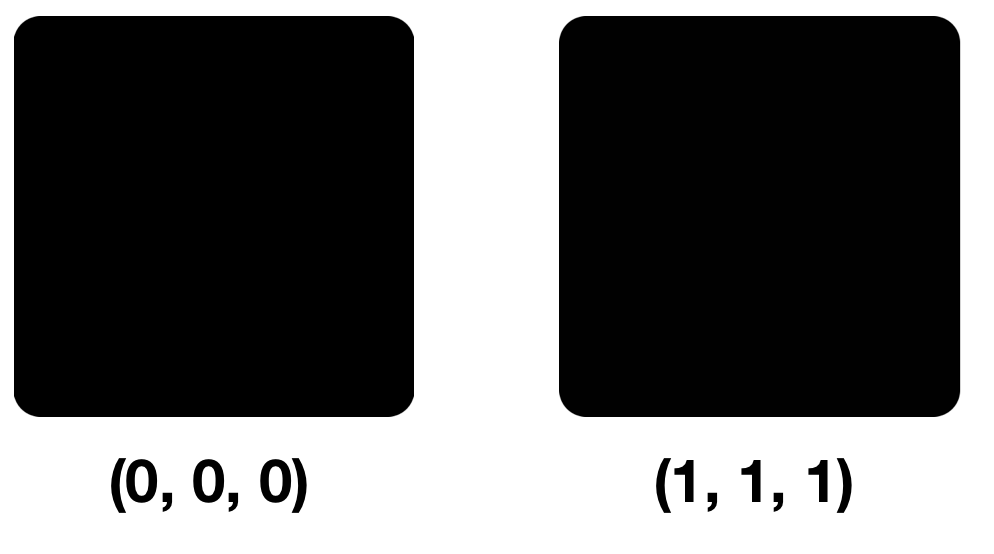
Geringe Pixelunterschiede auf den ersten, zweiten und dritten Blick sind nicht erkennbar. Tatsache ist, dass unser Auge ungefähr 10 Millionen Farben unterscheiden kann und das Gehirn nur ungefähr 150. Das RGB-Modell enthält auch 16.777.216 Farben. Sie können versuchen, sie alle hier zu unterscheiden .

Über die Befehlszeile

Es sind nicht viele Open Source-Befehlszeilentools verfügbar, die die LSB-Steganographie darstellen.

Die beliebtesten finden Sie in der folgenden Tabelle.

Wo ist die Katze?

Und der erste in der Liste der Angriffe auf die LSB-Steganographie ist ein visueller Angriff. Klingt komisch, nicht wahr? Immerhin hat sich die Katze mit dem Geheimnis auf den ersten Blick nicht als gefüllter Stegocontainer verraten. Hmmm ... Sie müssen nur wissen, wo Sie suchen müssen. Es ist leicht zu erraten, dass nur die NZB unsere Aufmerksamkeit verdient.

Für einen gefüllten Stegocontainer sieht das Bild mit NZB folgendermaßen aus:



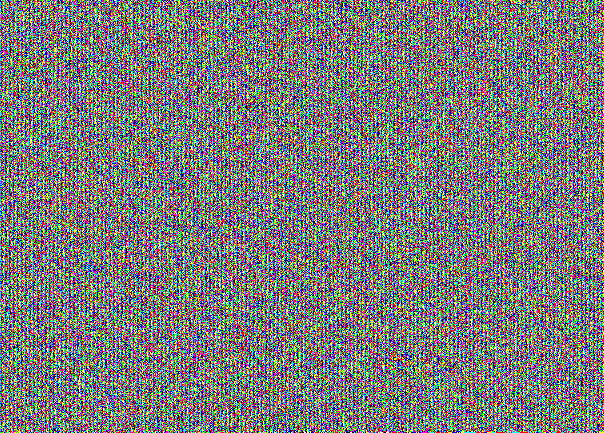
Glaubst du nicht? Hier haben Sie NZB von allen drei Kanälen getrennt:




Dies ist eine "Zeichnung", die speziell zum Ausblenden der Nachricht in der NZB dient. Auf den ersten Blick scheint dies ein einfaches Geräusch zu sein. Aber wenn man bedenkt, ist die Struktur sichtbar. Hier sehen Sie, dass der Stegocontainer voll ist. Wenn wir eine Nachricht mit 30% der Kapazität einer armen Katze aufnehmen würden, würden wir folgendes Bild erhalten:


Sein NZB:



~ 70% der Katze bleiben unverändert.

Hier lohnt es sich, einen kleinen Exkurs zu machen und über Größen zu sprechen. Was ist eine 30% Katze? Die Größe der Katze beträgt 603x433 Pixel. 30% dieser Größe sind 78459 Pixel. Jedes Pixel enthält 3 Informationsbits. Insgesamt 78459 3 = 235377 Bits oder etwas weniger als 30 Kilobyte passen in 30% der Dichtung. Und in die ganze Katze passen etwa 100 Kilobyte. Solche Dinge.

Aber wir sind aus einem bestimmten Grund für Sie da. Wie kann man dann die Augen täuschen?
Erster Gedanke: Stecke die Nachricht in den Lärm. Aber es war nicht da. Als nächstes folgt ein Fragment des gefüllten Stegocontainers und seines LSB.



Mit ein wenig Aufwand können wir immer noch eine vertraute Struktur erkennen. Verlieren Sie nicht die Hoffnung, meine Herren!

Hee hee hee

Viele Dinge brechen die Statistik, wissen Sie.

Wenn wir etwas im Bild ändern, ändern wir seine statistischen Eigenschaften. Es reicht für den Analysten aus, einen Weg zu finden, um diese Änderungen zu beheben.

Der gute alte Chi-Platz wurde von Andreas Wesfield und Andreas Pfitzmann von der Universität Dresden in ihrer Arbeit „Attacks on Steganographic Systems“ ins Leben gerufen, die hier zu finden ist.

Im Folgenden werden wir über Angriffe innerhalb derselben Farbebene oder im Kontext von RGB über Angriffe auf einen Kanal sprechen. Die Ergebnisse jedes Angriffs können auf den Durchschnitt reduziert werden und das Ergebnis für das „zusammengesetzte“ Bild erhalten.

Der Chi-Quadrat-Angriff basiert also auf der Annahme, dass die Wahrscheinlichkeit des gleichzeitigen Auftretens benachbarter (durch das niedrigstwertiges Bit unterschiedlicher) Farben (Wertepaare) in einem leeren Stegocontainer äußerst gering ist. Es ist wirklich so, man kann es glauben. Mit anderen Worten, die Anzahl der Pixel zweier benachbarter Farben unterscheidet sich für einen leeren Behälter erheblich. Wir müssen lediglich die Anzahl der Pixel jeder Farbe berechnen und einige Formeln anwenden. Tatsächlich ist dies eine einfache Aufgabe, um eine Hypothese unter Verwendung des Chi-Quadrat-Tests zu testen.

Ein bisschen Mathe?

Sei h ein Array an der i-ten Stelle, das die Anzahl der Pixel der i-ten Farbe in dem untersuchten Bild enthält.

Dann:

1. Gemessene Farbfrequenz $$$i = 2k$ ::
   

   $$

   $$n_k = h [2k], ~ k \ in [0, 127];$$
   
   
2. Theoretisch erwartete Farbfrequenz $$$i = 2k$ ::
   

   $$

   $$n_k ^ * = \ frac {h [2k] + h [2k + 1]} {2}, ~ k \ in [0,127];$$
   
   

Wenn Sie dies in Python übersetzen, erhalten Sie ungefähr Folgendes:

for k in range(0, len(histogram) // 2): expected.append(((histogram[2 * k] + histogram[2 * k + 1]) / 2)) observed.append(histogram[2 * k]) 

Wobei das Histogramm die Anzahl der Pixel der Farbe i im Bild ist, $$$i \ in [0, 255]$

Das Chi-Quadrat-Kriterium für die Anzahl der Freiheitsgrade k-1 wird wie folgt berechnet (k ist die Anzahl verschiedener Farben, d. H. 256):

$$

$$\ chi_ {k-1} ^ 2 = \ sum_ {i = 1} ^ {k} \ frac {(n_k - n_k ^ *) ^ 2} {n_k ^ *};$$

Und schließlich ist P die Wahrscheinlichkeit, dass die Verteilungen $$$n_i$ und $$$n_i ^ *$ Unter diesen Bedingungen sind sie gleich (die Wahrscheinlichkeit, dass wir einen gefüllten Stegocontainer haben). Sie wird durch Integration der Glättungsfunktion berechnet:

$$

$$P = 1 - \ frac {1} {2 ^ {\ frac {k-1} {2}} \ Gamma (\ frac {k-1} {2})} \ int_0 ^ {\ chi_ {k-1 } ^ 2} e ^ {- \ frac {x} {2}} x ^ {\ frac {k-1} {2} -1} dx;$$

Am effektivsten ist es, ein Chi-Quadrat nicht auf das gesamte Bild anzuwenden, sondern nur auf seine Teile, beispielsweise auf die Linien. Wenn die berechnete Wahrscheinlichkeit für die Linie größer als 0,5 ist, füllen Sie die Linie im Originalbild mit Rot. Wenn weniger, dann grün. Bei einer Katze mit 30% Fülle sieht das Bild wie folgt aus:



Ganz richtig, nicht wahr?

Nun, wir haben einen mathematisch fundierten Angriff, Sie können die Mathematik nicht täuschen! Oder ... ??

Mische Tanz

Die Idee ist ganz einfach: Schreiben Sie die Bits nicht in der richtigen Reihenfolge, sondern an zufälligen Stellen. Dazu müssen Sie das PRSP nehmen und so konfigurieren, dass es denselben zufälligen Stream mit derselben Seite (auch als Passwort bezeichnet) ausgibt. Ohne Kenntnis des Passworts können wir das PRNG nicht konfigurieren und die Pixel finden, in denen die Nachricht versteckt ist. Wir werden es an einer Katze testen.

Kätzchen (32% Abschluss):



Sein LSB:



Das Bild sieht laut aus, ist aber für einen unerfahrenen Analysten nicht verdächtig. Was sagt Chi-Quadrat?


Es scheint, der schwarze Hut hat gewonnen !? Egal wie ...

Regelmäßigkeit-Singularität

Eine weitere statistische Methode war 2001 Jessica Friedrich, Miroslav Golyan und Andreas Pfitzman. Es wurde als RS-Methode bezeichnet. Der Originalartikel kann hier genommen werden.

Das Verfahren enthält mehrere vorbereitende Schritte.

Das Bild ist in Gruppen von n Pixeln unterteilt. Zum Beispiel 4 aufeinanderfolgende Pixel in einer Reihe. Solche Gruppen enthalten in der Regel benachbarte Pixel.
Für unsere Katze mit sequentieller Füllung im roten Kanal sind die ersten fünf Gruppen:

• [78, 78, 79, 78]
  
• [78, 78, 78, 78]
  
• [78, 79, 78, 79]
  
• [79, 76, 79, 76]
  
• [76, 76, 76, 77]
  

(Alle Messungen sind in der klassischen Version von RGB)

Dann definieren wir die sogenannte Diskriminanzfunktion oder Glättungsfunktion, die jede Pixelgruppe einer reellen Zahl zuordnet. Der Zweck dieser Funktion besteht darin, die Glätte oder "Regelmäßigkeit" der Pixelgruppe G zu erfassen. Je lauter die Pixelgruppe ist $$$G = (x_1, ..., x_n)$ desto wichtiger wird die Diskriminanzfunktion sein. Am häufigsten wird eine "Variation" einer Gruppe von Pixeln gewählt, oder einfacher die Summe der Unterschiede benachbarter Pixel in einer Gruppe. Es können aber auch statistische Annahmen über das Bild berücksichtigt werden.

$$

$$f (x_1, x_2, ..., x_n) = \ sum_ {i = 1} ^ {n-1} | x_ {i + 1} - x_i |$$

Die Werte der Glättungsfunktion für eine Gruppe von Pixeln aus unserem Beispiel:

• f (78, 78, 79, 78) = 2
• f (78, 78, 78, 78) = 0
• f (78, 79, 78, 79) = 3
• f (79, 76, 79, 76) = 9
• f (76, 76, 76, 77) = 1

Als nächstes wird die Klasse der Flip-Funktionen von einem Pixel bestimmt.

Sie müssen einige Eigenschaften haben.

$$

$$1. ~~~ \ forall x \ in P: ~ F (F (x)) = x, ~~ P = \ {0, ~ 255 \};$$

$$

$$2. ~~~ F_1: 0 \ leftrightarrow 1, ~ 2 \ leftrightarrow 3, ~ ..., 254 \ leftrightarrow 255;$$

$$

$$3 ~~~ \ forall x \ in P: ~ F _ {- 1} (x) = F_1 (x + 1) -1;$$

Wo $$$F$ - jede Funktion aus einer Klasse, $$$F_1$ Ist eine direkte Flip-Funktion und $$$F _ {- 1}$ - umkehren. Außerdem wird üblicherweise die identische Flip-Funktion bezeichnet $$$F_0$ das ändert das Pixel nicht.

Die Python-Flip-Funktionen könnten ungefähr so ​​aussehen:

 def flip(val): if val & 1: return val - 1 return val + 1 def invert_flip(val): if val & 1: return val + 1 return val - 1 def null_flip(val): return val 

Für jede Pixelgruppe wenden wir eine der Flip-Funktionen an und bestimmen basierend auf dem Wert der Diskriminanzfunktion vor und nach dem Flip den Typ der Pixelgruppe: normal (regelmäßig), einzeln / ungewöhnlich (singulär) und unbrauchbar unbrauchbar. Da der letztere Typ nicht weiter verwendet wird, wurde die Methode nach den ersten Buchstaben der Schlüsseltypen benannt. Das ist das ganze Geheimnis des Namens, die Singularität hat nichts damit zu tun :)



Möglicherweise möchten wir unterschiedliche Pixel auf verschiedene Pixel anwenden. Dazu definieren wir eine Maske M mit n Werten von -1, 0 oder 1.

$$

$$F_M (G) = (F_ {M (1)} (x_1), F_ {M (2)} (x_2), ..., F_ {M (n)} (x_n))$$

Die Maske für unser Beispiel sei klassisch - [1, 0, 0, 1]. Es wurde experimentell festgestellt, dass symmetrische Masken, die nicht enthalten $$$F _ {- 1}$ . Ebenfalls erfolgreiche Optionen wären: [0, 1, 0, 1], [0, 1, 1, 0], [1, 0, 1, 0]. Wir wenden das Spiegeln für die Gruppen aus dem Beispiel an, berechnen den Glättungswert und bestimmen den Typ der Pixelgruppe:

• $$$F_m$ (78, 78, 79, 78) = [79, 78, 79, 79];
  f (79, 78, 79, 79) = 2 = 2 = f (78, 78, 79, 78)
  Nicht verwendbare Gruppe
  
  
• $$$F_m$ (78, 78, 78, 78) = [79, 78, 78, 79];
  f (79, 78, 78, 79) = 2> 0 = f (78, 78, 78, 78)
  Regelmäßige Gruppe
  
  
• $$$F_m$ (78, 79, 78, 79) = [79, 79, 78, 78];
  f (79, 79, 78, 78) = 1 <3 = f (78, 79, 78, 79) Singuläre Gruppe
  
  
• $$$F_m$ (79, 76, 79, 76) = [78, 76, 79, 77];
  f (78, 76, 79, 77) = 7 <9 = f (79, 76, 79, 76) Singuläre Gruppe
  
  
• $$$F_m$ (76, 76, 76, 77) = [77, 76, 76, 76];
  f (77, 76, 76, 76) = 1 = 1 = f (76, 76, 76, 77)
  Nicht verwendbare Gruppe
  
  

Wir bezeichnen die Anzahl der regulären Gruppen für die Maske M als $$$R_M$ (in Prozent aller Gruppen) und $$$S_M$ für einzelne Gruppen.

Dann $$$R_M + S_M \ leq 1$ und $$$R _ {- M} + S _ {- M} \ leq 1$ für eine negative Maske (alle Maskenkomponenten werden mit -1 multipliziert), weil $$$R_M + S_M + U_M = 1$ , dabei $$$U_M$ kann leer sein. Ähnliches gilt für eine negative Maske.

Die wichtigste statistische Hypothese ist, dass in einem typischen Bild der erwartete Wert $$$R_M$ gleich $$$R _ {- M}$ und das gleiche gilt für $$$S_M$ und $$$S _ {- M}$ . Dies wird durch experimentelle Daten und einige Tänze mit einem Tamburin um die letzte Eigenschaft der Flip-Funktion bewiesen.

$$

$$R_M \ cong S_M ~~~~ R _ {- M} \ cong S _ {- M}$$

Schauen wir uns unser kleines Beispiel an. Angesichts der geringen Stichprobengröße können wir diese Hypothese möglicherweise nicht bestätigen. Mal sehen, was mit der invertierten Maske passiert: [-1, 0, 0, -1].

• F_M (78, 78, 79, 78) = [77, 78, 79, 77];
  f (77, 78, 79, 77) = 4> 2 = f (77, 78, 79, 77)
  Regelmäßige Gruppe
  
  
• F_M (78, 78, 78, 78) = [77, 78, 78, 77];
  f (77, 78, 78, 77) = 2> 0 = f (78, 78, 78, 78)
  Regelmäßige Gruppe
  
  
• F_M (78, 79, 78, 79) = [77, 79, 78, 80];
  f (77, 79, 78, 80) = 5> 3 = f (78, 79, 78, 79)
  Regelmäßige Gruppe
  
  
• F_M (79, 76, 79, 76) = [80, 76, 79, 75];
  f (80, 76, 79, 75) = 11> 9 = f (79, 76, 79, 76)
  Regelmäßige Gruppe
  
  
• F_M (76, 76, 76, 77) = [75, 76, 76, 78];
  f (75, 76, 76, 78) = 3> 1 = f (76, 76, 76, 77)
  Regelmäßige Gruppe
  
  

Nun, alles ist offensichtlich.

Allerdings ist der Unterschied zwischen $$$R_M$ und $$$S_M$ neigen zu Null, wenn die Länge m der eingebetteten Nachricht zunimmt und wir das bekommen $$$R_M \ cong S_M$ .

Es ist lustig, dass die Randomisierung der LSB-Ebene den gegenteiligen Effekt hat $$$R _ {- M}$ und $$$S _ {- M}$ . Ihre Differenz nimmt mit der Länge m der eingebetteten Nachricht zu. Eine Erklärung dieses Phänomens finden Sie im Originalartikel.

Hier ist der Zeitplan $$$R_M$ , $$$S_M$ , $$$R _ {- M}$ und $$$S _ {- M}$ Abhängig von der Anzahl der Pixel mit invertierten LSBs wird es als RS-Diagramm bezeichnet. Die x-Achse ist der Prozentsatz der Pixel mit invertierten LSBs, die y-Achse ist die relative Anzahl der regulären und singulären Gruppen mit den Masken M und -M. $$$M = [0 ~ 1 ~ 1 ~ 0]$ .



Die RS-Steganalyse besteht im Wesentlichen darin, die vier Kurven des RS-Diagramms auszuwerten und ihren Schnittpunkt mithilfe von Extrapolation zu berechnen. Angenommen, wir haben einen Stegocontainer mit einer Nachricht unbekannter Länge p (als Prozentsatz der Pixel), die in die unteren Bits zufällig ausgewählter Pixel eingebettet ist (d. H. Unter Verwendung von RandomLSB). Unsere ersten Messungen der Anzahl der Gruppen R und S entsprechen Punkten $$$R_M (p / 2)$ , $$$S_M (p / 2)$ , $$$R _ {- M} (p / 2)$ und $$$S _ {- M} (p / 2)$ . Wir nehmen Punkte von genau der halben Länge der Nachricht, da die Nachricht ein zufälliger Bitstrom ist und im Durchschnitt, wie bereits erwähnt, nur die Hälfte der Pixel durch Einbetten der Nachricht geändert wird.

Wenn wir das LSB aller Pixel im Bild invertieren und die Anzahl der R- und S-Gruppen berechnen, erhalten wir vier Punkte $$$R_M (1-p / 2)$ , $$$S_M (1-p / 2)$ , $$$R _ {- M} (1-p / 2)$ und $$$S _ {- M} (1-p / 2)$ . Da diese beiden Punkte von der spezifischen Randomisierung des LSB abhängen, müssen wir diesen Vorgang viele Male wiederholen und bewerten $$$R_M (1/2)$ und $$$S_M (1/2)$ aus statistischen Stichproben.

Wir können bedingt Linien durch Punkte ziehen $$$R _ {- M} (p / 2)$ , $$$R _ {- M} (1-p / 2)$ und $$$S _ {- M} (p / 2)$ , $$$S _ {- M} (1-p / 2)$ .

Punkte $$$R_M (p / 2)$ , $$$R_M (1/2)$ , $$$R_M (1-p / 2)$ und $$$S_M (p / 2)$ , $$$S_M (1/2)$ , $$$S_M (1-p / 2)$ Definieren Sie zwei Parabeln. Jede Parabel und die entsprechende Linie schneiden sich links. Das arithmetische Mittel der x-Koordinaten beider Schnittpunkte ermöglicht es uns, die unbekannte Nachrichtenlänge p abzuschätzen.

Um eine lange statistische Schätzung der Mittelpunkte RM (1/2) und SM (1/2) zu vermeiden, können einige weitere Überlegungen angestellt werden:

1. Kurvenschnittpunkt $$$R_M$ und $$$R _ {- M}$ hat die gleiche x-Koordinate wie der Schnittpunkt für die Kurven $$$S_M$ und $$$S _ {- M}$ . Dies ist im Wesentlichen eine strengere Version unserer statistischen Hypothese. (siehe oben)
2. Die RM- und SM-Kurven schneiden sich bei m = 50% oder $$$R_M (1/2) = S_M (1/2)$ .

Diese beiden Annahmen liefern eine einfache Formel für die Länge der geheimen Nachricht p. Nachdem die x-Achse so skaliert wurde, dass p / 2 zu 0 und 1 - p / 2 zu 1 wird, ist die x-Koordinate des Schnittpunkts die Wurzel der folgenden quadratischen Gleichung



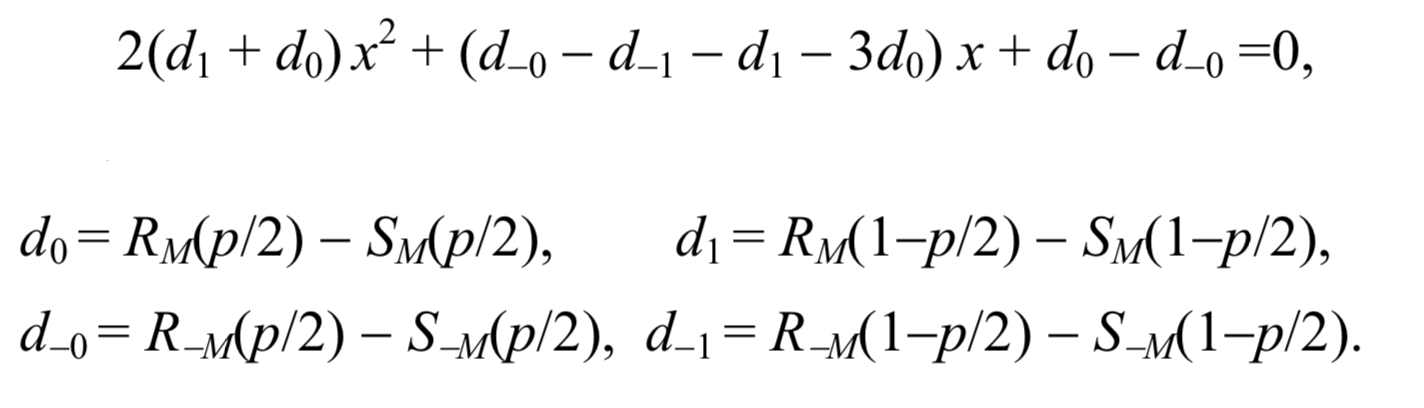
Dann kann die Nachrichtenlänge durch die Formel berechnet werden:

$$

$$p = \ frac {x} {x- \ frac {1} {2}}$$

Hier betritt unsere Katze die Szene. (Ist es nicht Zeit, ihm einen Namen zu geben?)

Also haben wir:

• Regelmäßige RM-Gruppen (p / 2): 23121 Stk.
• Singuläre SM-Gruppen (p / 2): 14124 Stk.
• Regelmäßige Gruppen mit umgekehrter Maske RM (p / 2): 37191 Stk.
• Einzelgruppen mit umgekehrter Maske SM (p / 2): 8440 Stk.
• Regelmäßige Gruppen mit invertiertem LSB RM (1-p / 2): 20298 Stk.
• Einzelgruppen mit invertiertem LSB SM (1-p / 2): 16206 Stk.
• Regelmäßige Gruppen mit invertiertem LSB und invertierter Maske RM (1-p / 2): 40603 Stk.
• Einzelne Gruppen mit invertiertem LSB und mit invertierter Maske SM (1-p / 2): 6947 Stk.

(Wenn Sie viel Freizeit haben, können Sie diese selbst berechnen, aber ich schlage vor, Sie glauben meinen Berechnungen.)

Auf der Tagesordnung haben wir eine bloße Mathematik gelassen. Erinnern Sie sich noch daran, wie man quadratische Gleichungen löst?

$$

$$d_0 = 8997$$

$$

$$d _ {- 0} = $ 2875$$

$$

$$d_1 = 4092$$

$$

$$d _ {- 1} = 33656$$

Wenn wir alle d in der obigen Formel einsetzen, erhalten wir eine quadratische Gleichung, die wir wie in der Schule gelehrt lösen.

$$

$$26178x ^ 2-35988x - 19754 = 0$$

$$

$$D = (-35988) ^ 2 - 426178 * (- 19754) = $ 336361699$$

$$

$$x_1 = 1.7951 ~~~~~~~~ x_2 = -0.4204$$

Nehmen Sie eine Wurzel mit kleinerem Modul, d.h. $$$x_2$ . Dann ist die ungefähre Schätzung für die in die Katze eingebaute Nachricht folgende:

$$

$$p = \ frac {-0,4204} {- 0,4204 - 0,5} = 0,4567$$

Ja, diese Methode hat ein großes Plus und ein großes Minus. Der Vorteil ist, dass die Methode sowohl mit der gewöhnlichen LSB-Steganographie als auch mit der RandomLSB-Steganographie funktioniert. Ein Chi-Quadrat kann sich einer solchen Gelegenheit nicht rühmen. Die Methode erkannte unsere zufällig aussehende Katze genau und schätzte die Nachrichtenlänge auf 0,3256, was sehr, sehr genau ist.

Das Minus liegt im großen (sehr großen) Fehler dieser Methode, der mit der langen Nachricht mit sequentieller Einbettung wächst. Zum Beispiel ergibt meine Implementierung der Methode für eine Katze mit einer Belegung von 30% eine ungefähre durchschnittliche Schätzung für drei Kanäle von 0,4633 oder 46% der Gesamtkapazität bei einer Belegung von mehr als 95% - 0,8597. Aber für eine leere Katze bis zu 0,0054. Und dies ist ein allgemeiner Trend, der unabhängig von der Umsetzung ist. Die genauesten Ergebnisse mit der normalen LSB-Methode ergeben eine integrierte Nachrichtenlänge von 10% + - 5%.

Plus oder Minus

Um nicht erwischt zu werden, muss man unerwartet sein und ± 1 Codierung verwenden. Anstatt das niedrigstwertige Bit im Farbbyte zu ändern, erhöhen oder verringern wir das gesamte Byte um eins. Es gibt nur zwei Ausnahmen:

• wir können Null nicht reduzieren, deshalb werden wir sie erhöhen,
  
• Wir können 255 auch nicht erhöhen, daher werden wir diesen Wert immer verringern.
  

Für alle anderen Bytewerte wählen wir entweder zufällig eine Erhöhung um eins oder eine Verringerung aus. Zusätzlich zu dieser Manipulation ändert sich das LSB wie zuvor. Für eine höhere Zuverlässigkeit ist es besser, zufällige Bytes zum Aufzeichnen einer Nachricht zu verwenden.

Hier ist unsere Freundin Katze:



Äußerlich ist die Einleitung aus demselben Grund unmerklich genau, warum die Unterschiede zwischen (0, 0, 0) und (1, 1, 1) nicht sichtbar waren.



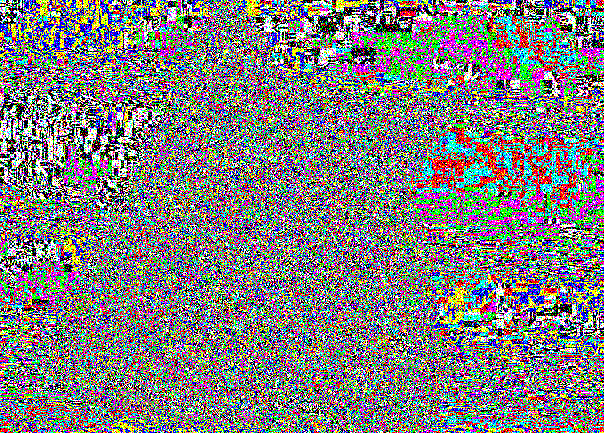
Das LSB-Slice bleibt aufgrund der Aufnahme an zufälligen Stellen einfach verrauscht.



Das Chi-Quadrat ist immer noch blind und die RS-Methode ergibt eine grobe Schätzung von 0,0036 .

Um nicht sehr glücklich zu sein, lesen Sie diesen Artikel hier.

Die aufmerksamsten fragen sich möglicherweise, wie wir eine Nachricht erhalten können, wenn ganze Bytes zufällig geändert werden, und wir haben kein Passwort zum Festlegen des PRNG (es ist besser, verschiedene Seeds, auch bekannt als den Status des Generators oder Passwörter, für die Arbeit mit RandomLSB und ± 1-Codierung zu verwenden). Die Antwort ist so einfach wie möglich. Wir erhalten die Nachricht genauso wie ohne ± 1 Codierung. Wir wissen möglicherweise nicht einmal über seine Verwendung. Ich wiederhole, wir verwenden diesen Trick nur, um automatische Erkennungswerkzeuge zu umgehen . Beim Einbetten / Abrufen einer Nachricht arbeiten wir nur mit ihrem LSB und nicht mehr. Bei der Erkennung müssen wir jedoch den Implementierungskontext berücksichtigen, dh alle Bytes des Bildes, um statistische Schätzungen zu erstellen. Dies ist genau der gesamte Erfolg der ± 1-Codierung.

Anstelle einer Schlussfolgerung

Ein weiterer sehr guter Versuch, Statistiken gegen die LSB-Steganographie zu verwenden, wurde mit einer Methode namens Sample Pairs unternommen. Sie finden es hier. Seine Anwesenheit hier würde den Artikel zu akademisch machen, deshalb lasse ich ihn für das außerschulische Lesen interessiert. Aber im Vorgriff auf die Fragen des Publikums werde ich sofort antworten: Nein, er fängt keine ± 1-Codierung ab.

Und natürlich maschinelles Lernen. Moderne Methoden, die auf ML basieren, liefern sehr gute Ergebnisse. Sie können hier und hier darüber lesen.

Basierend auf diesem Artikel wurde (vorerst) ein kleines Tool geschrieben. Es kann Daten generieren, einen visuellen Angriff separat auf die Kanäle ausführen, die RS-, SPA-Bewertung berechnen und die Ergebnisse des Chi-Quadrats visualisieren. Und sie wird dort nicht aufhören.

Zusammenfassend möchte ich ein paar Tipps geben:

• Betten Sie die Nachricht in zufällige Bytes ein.
• Reduzieren Sie die Menge der eingebetteten Informationen so weit wie möglich (denken Sie an Onkel Hamming).
• Verwenden Sie ± 1 Codierung.
• Wählen Sie Bilder mit verrauschtem LSB.
• Remdalps UPD: Verwenden Sie Bilder, die nirgendwo erscheinen.
• Sei nett!

Ich freue mich über Ihre Vorschläge, Ergänzungen, Korrekturen und sonstigen Rückmeldungen!

PS Ich möchte mich ganz besonders bei PavelMSTU für die Beratungen und Motivationskicks bedanken .