Eine einfache Einführung in ALU für neuronale Netze: Erklärung, physikalische Bedeutung und Implementierung

Kürzlich veröffentlichten Forscher von Google DeepMind, darunter ein bekannter Wissenschaftler für künstliche Intelligenz, Autor des Buches " Understanding Deep Learning ", Andrew Trask, einen beeindruckenden Artikel, der ein neuronales Netzwerkmodell zur Extrapolation der Werte einfacher und komplexer numerischer Funktionen mit hoher Genauigkeit beschreibt.

In diesem Beitrag werde ich die Architektur von NALU (Neural Arithmetic Logic Devices , NALU), ihre Komponenten und signifikante Unterschiede zu herkömmlichen neuronalen Netzen erläutern. Das Hauptziel dieses Artikels ist es, NALU (sowohl Implementierung als auch Idee) für Wissenschaftler, Programmierer und Studenten, die mit neuronalen Netzen und tiefem Lernen noch nicht vertraut sind, einfach und intuitiv zu erklären.

Anmerkung des Autors : Ich empfehle außerdem dringend, den Originalartikel zu lesen, um das Thema genauer zu studieren.

Wann sind neuronale Netze falsch?

Bild aus diesem Artikel.

Theoretisch sollten neuronale Netze Funktionen gut approximieren. Sie sind fast immer in der Lage, signifikante Übereinstimmungen zwischen Eingabedaten (Faktoren oder Merkmale) und Ausgaben (Beschriftungen oder Ziele) zu identifizieren. Aus diesem Grund werden neuronale Netze in vielen Bereichen eingesetzt, von der Objekterkennung und ihrer Klassifizierung über die Übersetzung von Sprache in Text bis hin zur Implementierung von Spielalgorithmen, die Weltmeister schlagen können. Es wurden bereits viele verschiedene Modelle erstellt: Faltungs- und wiederkehrende neuronale Netze, Autocodierer usw. Der Erfolg bei der Erstellung neuer Modelle für neuronale Netze und Deep Learning ist ein großes Thema für sich.

Laut den Autoren des Artikels bewältigen neuronale Netze jedoch nicht immer Aufgaben, die für Menschen und sogar Bienen offensichtlich erscheinen! Dies ist beispielsweise ein mündlicher Bericht oder eine Operation mit Zahlen sowie die Fähigkeit, die Abhängigkeit von Beziehungen zu identifizieren. Der Artikel zeigte, dass Standardmodelle neuronaler Netze nicht einmal mit der identischen Zuordnung fertig werden können (eine Funktion, die ein Argument in sich selbst übersetzt). $$$f (x) = x$) Ist die offensichtlichste numerische Beziehung. Die folgende Abbildung zeigt die MSE verschiedener Modelle neuronaler Netze beim Lernen der Werte dieser Funktion.


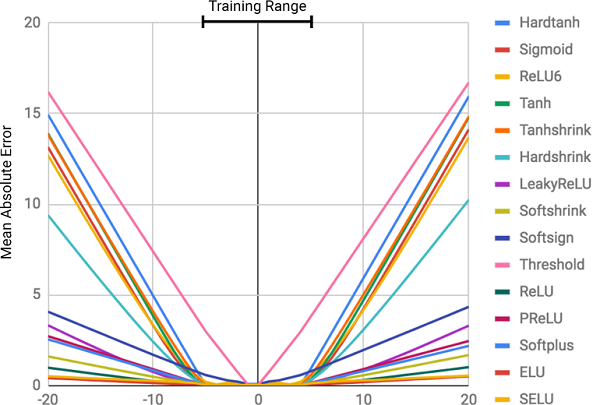Die Abbildung zeigt den mittleren quadratischen Fehler für neuronale Standardnetzwerke, die dieselbe Architektur und unterschiedliche (nichtlineare) Aktivierungsfunktionen in den inneren Schichten verwenden

Warum sind neuronale Netze falsch?

Wie aus der Figur ersichtlich ist, ist der Hauptgrund für Fehlschläge die Nichtlinearität der Aktivierungsfunktionen auf den inneren Schichten des neuronalen Netzwerks. Dieser Ansatz eignet sich hervorragend zum Bestimmen nichtlinearer Beziehungen zwischen Eingabedaten und Antworten, aber es ist schrecklich falsch, über die Daten hinauszugehen, auf denen das Netzwerk gelernt hat. Neuronale Netze können sich also hervorragend an eine numerische Abhängigkeit von Trainingsdaten erinnern , können diese jedoch nicht extrapolieren.

Dies ist so, als würde man eine Antwort oder ein Thema vor einer Prüfung stopfen, ohne das Thema zu verstehen. Es ist leicht, den Test zu bestehen, wenn die Fragen den Hausaufgaben ähnlich sind, aber wenn es das Verständnis des zu testenden Themas ist und nicht die Fähigkeit, sich zu erinnern, werden wir scheitern.


Dies war nicht im Kursprogramm!

Der Fehlergrad steht in direktem Zusammenhang mit dem Grad der Nichtlinearität der ausgewählten Aktivierungsfunktion. Das vorige Diagramm zeigt deutlich, dass nichtlineare Funktionen mit harten Einschränkungen wie einem Sigmoid oder einer hyperbolischen Tangente ( Tanh ) die Aufgabe bewältigen können, die Abhängigkeiten viel schlimmer zu verallgemeinern als Funktionen mit weichen Einschränkungen, wie z. B. eine abgeschnittene lineare Transformation ( ELU , PReLU ).

Lösung: Neuronale Batterie (NAC)

Eine neuronale Batterie ( NAC ) ist das Herzstück des NALU- Modells. Dies ist ein einfacher, aber effektiver Teil eines neuronalen Netzwerks, das mit Addition und Subtraktion fertig wird , was für die effiziente Berechnung linearer Beziehungen erforderlich ist.

NAC ist eine spezielle lineare Schicht eines neuronalen Netzwerks, für deren Gewicht eine einfache Bedingung auferlegt wird: Sie können nur 3 Werte annehmen - 1, 0 oder -1 . Aufgrund solcher Einschränkungen kann die Batterie den Bereich der Eingabedaten nicht ändern und bleibt auf allen Ebenen des Netzwerks unabhängig von Anzahl und Verbindungen konstant. Somit ist die Ausgabe eine lineare Kombination der Werte des Eingabevektors, was leicht eine Additions- und Subtraktionsoperation sein kann.

Laute Gedanken : Zum besseren Verständnis dieser Aussage betrachten wir ein Beispiel für den Aufbau von Schichten eines neuronalen Netzwerks, die lineare arithmetische Operationen an Eingabedaten ausführen.


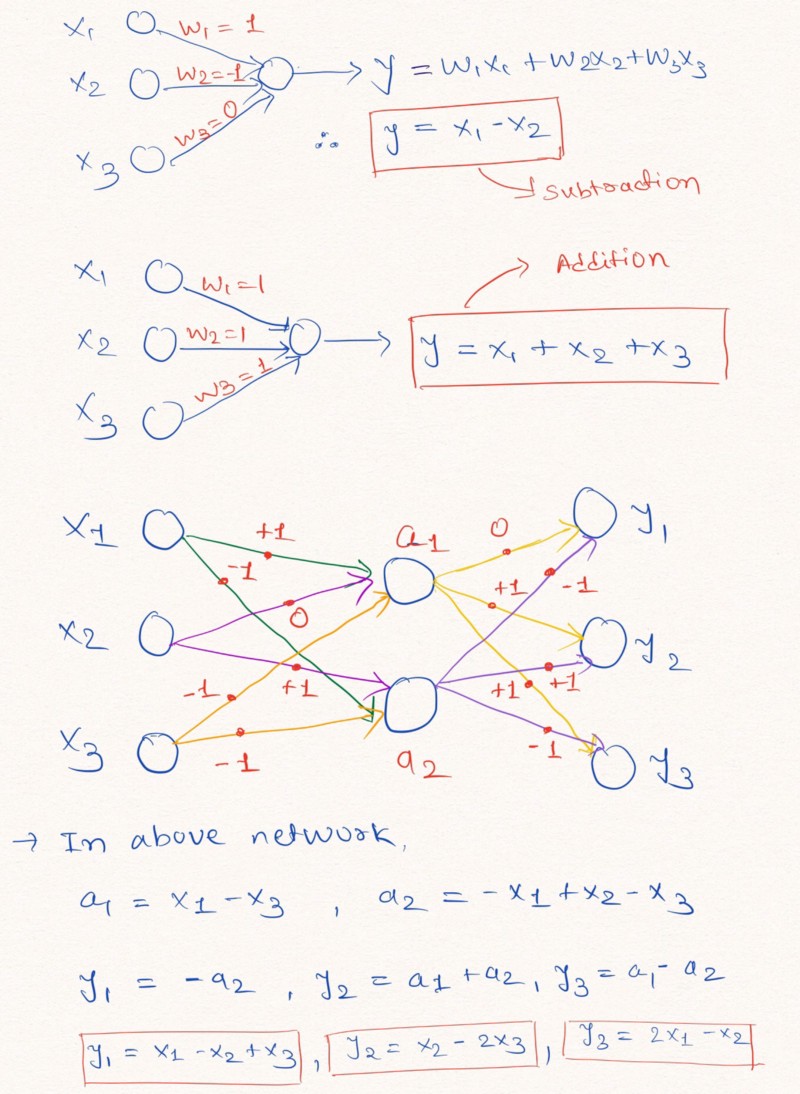Die Abbildung zeigt, wie Schichten eines neuronalen Netzwerks ohne Hinzufügen einer Konstanten und mit möglichen Werten der Gewichte -1, 0 oder 1 eine lineare Extrapolation durchführen können

Wie oben im Bild der Schichten gezeigt, kann das neuronale Netzwerk lernen, die Werte solcher einfachen arithmetischen Funktionen wie Addition und Subtraktion zu extrapolieren ( $$$y = x_1 + x_2$und $$$y = x_1 - x_2$) unter Verwendung der Beschränkungen der Gewichte mit möglichen Werten von 1, 0 und -1.

Hinweis: Die NAC-Schicht enthält in diesem Fall keinen freien Term (Konstante) und wendet keine nichtlinearen Transformationen auf die Daten an.

Da Standard-Neuronale Netze die Lösung des Problems unter ähnlichen Einschränkungen nicht bewältigen können, bieten die Autoren des Artikels eine sehr nützliche Formel zur Berechnung solcher Parameter durch klassische (unbegrenzte) Parameter $$$\ hat {W}$und $$$\ hat {M}$. Gewichtsdaten können wie alle Parameter neuronaler Netze zufällig initialisiert und während des Trainings des Netzes ausgewählt werden. Formel zur Berechnung des Vektors $$$W$durch $$$\ hat {W}$und $$$\ hat {M}$sieht so aus:

$$

$$W = tanh (\ hat {W}) \ odot \ sigma (\ hat {M})$$

Die Formel verwendet das elementweise Matrixprodukt

Die Verwendung dieser Formel stellt sicher, dass der Bereich der W-Werte auf das Intervall [-1, 1] begrenzt ist, das näher an der Menge -1, 0, 1 liegt. Außerdem können Funktionen aus dieser Gleichung durch Gewichtsparameter unterschieden werden. Somit wird es für unsere NAC- Schicht einfacher sein, Werte zu lernen $$$W$unter Verwendung von Gradientenabstieg und Rückausbreitung von Fehlern . Das Folgende ist ein Diagramm der Architektur der NAC- Schicht.


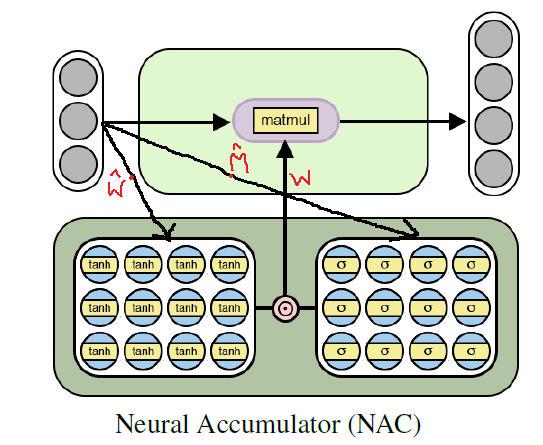Die Architektur einer neuronalen Batterie für das Training elementarer (linearer) arithmetischer Funktionen

Python NAC-Implementierung mit Tensorflow

Wie wir bereits verstanden haben, ist NAC ein ziemlich einfaches neuronales Netzwerk (Netzwerkschicht) mit kleinen Merkmalen. Das Folgende ist eine Implementierung einer NAC- Schicht in Python unter Verwendung der Bibliotheken Tensoflow und NumPy.


Im obigen Code $$$\ hat {W}$und $$$\ hat {M}$werden unter Verwendung einer gleichmäßigen Verteilung initialisiert, Sie können jedoch jede empfohlene Methode zum Generieren einer anfänglichen Näherung für diese Parameter verwenden. Sie können die Vollversion des Codes in meinem GitHub-Repository sehen (der Link wird am Ende des Beitrags dupliziert).

Weiter geht's: Von Addition und Subtraktion zu NAC für komplexe arithmetische Ausdrücke

Obwohl das oben beschriebene Modell eines einfachen neuronalen Netzwerks mit den einfachsten Operationen wie Addition und Subtraktion zurechtkommt, müssen wir aus den vielen Bedeutungen komplexerer Funktionen wie Multiplikation, Division und Exponentiation lernen können.

Im Folgenden finden Sie die modifizierte NAC- Architektur, die für die Auswahl komplexerer arithmetischer Operationen durch Logarithmus und die Aufnahme des Exponenten in das Modell angepasst ist. Beachten Sie die Unterschiede zwischen dieser NAC- Implementierung und der bereits oben diskutierten.


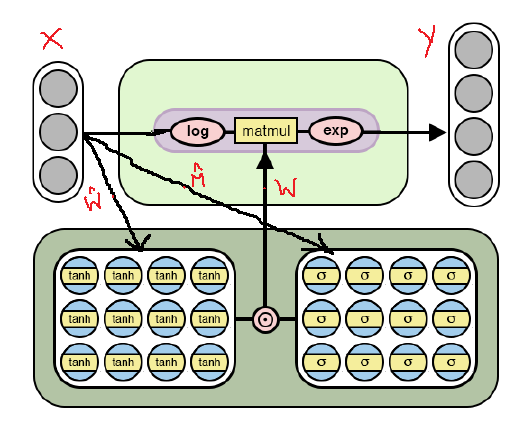NAC- Architektur für komplexere arithmetische Operationen

Wie aus der Abbildung ersichtlich ist, logarithmieren wir die Eingabedaten, bevor wir sie mit der Gewichtungsmatrix multiplizieren, und berechnen dann den Exponenten des Ergebnisses. Die Formel für die Berechnungen lautet wie folgt:

$$

$$Y = exp (W \ bullet (log (| x | + \ epsilon)))$$

Die Ausgabeformel für die zweite Version von NAC . $$$\ epsilon$Hier ist eine sehr kleine Zahl, um Situationen wie log (0) während des Trainings zu vermeiden

Somit gilt für beide NAC- Modelle das Funktionsprinzip, einschließlich der Berechnung der Gewichtsmatrix mit Einschränkungen $$$W$durch $$$\ hat {W}$und $$$\ hat {M}$ändert sich nicht. Der einzige Unterschied ist die Verwendung logarithmischer Operationen für die Eingabe und Ausgabe im zweiten Fall.

Zweite NAC-Version in Python mit Tensorflow

Der Code wird sich wie die Architektur kaum ändern, mit Ausnahme der angegebenen Verbesserungen bei der Berechnung des Tensors der Ausgabewerte.



Ich erinnere Sie noch einmal daran, dass sich die Vollversion des Codes in meinem GitHub-Repository befindet (der Link wird am Ende des Beitrags dupliziert).

Alles zusammen: eine neuronale arithmetische Logikeinheit (NALU)

Wie viele bereits vermutet haben, können wir aus fast jeder arithmetischen Operation lernen, indem wir die beiden oben diskutierten Modelle kombinieren. Dies ist die Hauptidee von NALU , die eine gewichtete Kombination aus elementarem und komplexem NAC umfasst , die über ein Trainingssignal gesteuert wird. Daher sind NACs die Bausteine ​​für die Erstellung von NALUs . Wenn Sie deren Design verstehen, ist die Erstellung von NALUs einfach. Wenn Sie noch Fragen haben, lesen Sie die Erklärungen für beide NAC- Modelle erneut. Unten sehen Sie ein Diagramm mit der NALU- Architektur.


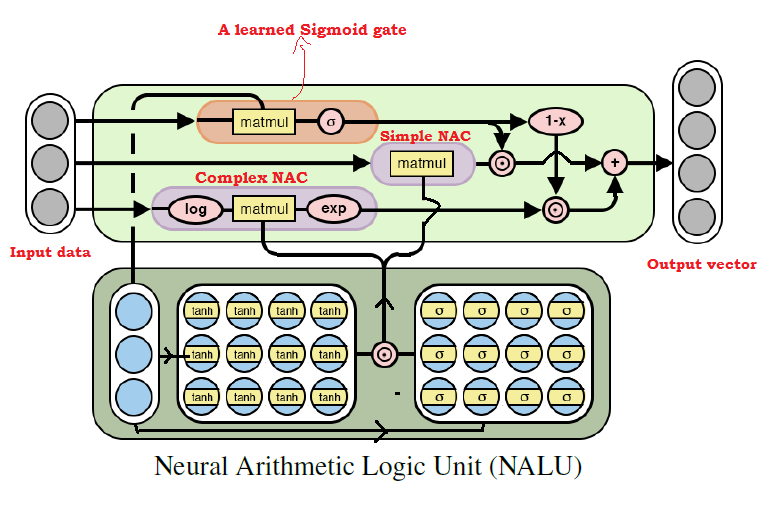NALU- Architekturdiagramm mit Erläuterungen

Wie aus der obigen Abbildung ersichtlich ist, werden beide NAC- Einheiten (lila Blöcke) innerhalb der NALU durch das Trainingssignal-Sigmoid (orangefarbener Block) interpoliert (kombiniert). Auf diese Weise können Sie die Ausgabe von jedem von ihnen abhängig von der arithmetischen Funktion, deren Werte wir zu finden versuchen, (de) aktivieren.

Wie oben erwähnt, ist die NAC- Elementareinheit eine Akkumulationsfunktion, die es der NALU ermöglicht, elementare lineare Operationen (Addition und Subtraktion) auszuführen, während die komplexe NAC-Einheit für Multiplikation, Division und Exponentiation verantwortlich ist. Die Ausgabe in NALU kann als Formel dargestellt werden:


Aus der obigen NALU- Formel können wir das mit schließen $$$g = 0$Das neuronale Netzwerk wählt nur Werte für komplexe arithmetische Operationen aus, nicht jedoch für elementare. und umgekehrt - im Fall von $$$g = 1$. Somit kann NALU im Allgemeinen jede arithmetische Operation lernen, die aus Addition, Subtraktion, Multiplikation, Division und Erhöhen zu einer Potenz besteht, und das Ergebnis erfolgreich über die Grenzen der Intervalle der Werte der Quelldaten hinaus extrapolieren.

Python NALU-Implementierung mit Tensorflow

Bei der Implementierung von NALU werden wir das elementare und komplexe NAC verwenden , das wir bereits definiert haben.


Ich stelle erneut fest, dass ich im obigen Code die Parametermatrix erneut initialisiert habe $$$G$Verwenden Sie eine gleichmäßige Verteilung, aber Sie können jede empfohlene Methode verwenden, um eine anfängliche Annäherung zu generieren.

---

Zusammenfassung

Für mich persönlich ist die Idee von NALU ein großer Durchbruch auf dem Gebiet der KI, insbesondere in neuronalen Netzen, und sie sieht vielversprechend aus. Dieser Ansatz kann die Tür zu den Anwendungsbereichen öffnen, in denen Standard-Neuronale Netze nicht zurechtkommen könnten.

Die Autoren des Artikels sprechen über verschiedene Experimente mit NALU : von der Auswahl der Werte elementarer arithmetischer Funktionen bis zur Zählung der Anzahl handgeschriebener Ziffern in einer bestimmten Reihe von MNIST- Bildern, mit denen neuronale Netze Computerprogramme überprüfen können!

Die Ergebnisse machen einen beeindruckenden Eindruck und beweisen, dass NALU fast alle Aufgaben im Zusammenhang mit der numerischen Darstellung besser bewältigt als Standardmodelle neuronaler Netze. Ich ermutige die Leser, sich mit den Ergebnissen von Experimenten vertraut zu machen, um besser zu verstehen, wie und wo das NALU- Modell nützlich sein kann.

Es muss jedoch beachtet werden, dass weder NAC noch NALU die ideale Lösung für eine Aufgabe sind. Sie repräsentieren vielmehr die allgemeine Idee, wie Modelle für eine bestimmte Klasse von arithmetischen Operationen erstellt werden können.

---

Unten finden Sie einen Link zu meinem GitHub-Repository, das die vollständige Implementierung des Codes aus dem Artikel enthält.
github.com/faizan2786/nalu_implementation

Sie können die Funktionsweise meines Modells für verschiedene Funktionen unabhängig überprüfen, indem Sie Hyperparameter für ein neuronales Netzwerk auswählen. Bitte stellen Sie Fragen und teilen Sie Ihre Gedanken in den Kommentaren unter diesem Beitrag, und ich werde mein Bestes tun, um Ihnen zu antworten.

PS (vom Autor): Dies ist mein erster schriftlicher Beitrag. Wenn Sie also Tipps, Vorschläge und Empfehlungen für die Zukunft haben (sowohl technische als auch allgemeine), schreiben Sie mir bitte.

PPS (vom Übersetzer): Wenn Sie Kommentare zur Übersetzung oder zum Text haben, schreiben Sie mir bitte eine persönliche Nachricht. Ich interessiere mich besonders für den Wortlaut des gelernten Gate-Signals - ich bin mir nicht sicher, ob ich diesen Begriff genau übersetzen kann.