Bestimmung der Anzahl der Stockwerke eines Hauses aus seinem Foto ohne maschinelles Lernen

In diesem Artikel werde ich meiner Meinung nach eine interessante Lösung für das Problem der Computererkennung von Objekten in einem Bild ohne Schulung geben.

Aufgabe: Wenn Sie ein Foto eines mehrstöckigen Gebäudes haben, versuchen Sie, die Anzahl der Stockwerke zu bestimmen.

Eine gute Schätzung für die Anzahl der Stockwerke kann die Anzahl der Fenster in der Vertikalen des Hauses angeben. Fenster, Balkone und andere Gegenstände sind gute Eigenschaften von Fußböden (insbesondere in Wohngebäuden). Ich werde Wohngebäude betrachten, deren Bilder im Netzwerk leicht zu finden sind. Eine wichtige Einschränkung sollte im Voraus beachtet werden: Das Haus im Bild muss vollständig vertikal dargestellt werden, damit alle Stockwerke visuell erfasst werden können.

Die Aufgabe ist rational in zwei Phasen unterteilt:

1. Suchen Sie nach dem vertikalen „Streifen“ der zu zählenden Fenster. Zwei Unteraufgaben: Erstens müssen Sie im Bildbereich des Hauses nach Fenstern suchen, und zweitens gibt es viele Fenster in Wohngebäuden. Es macht keinen Sinn, alle zu analysieren. Es ist notwendig, unter ihnen die vertikale Sequenz hervorzuheben, die für die nachfolgende Analyse am besten geeignet ist.
2. Bestimmung der Anzahl der Stockwerke (Fenster oder andere charakteristische Objekte) durch den ausgewählten Bereich des Hauses.

Dieser Artikel ist hauptsächlich dem ersten Schritt der Lösung gewidmet. Der zweite Schritt befindet sich noch in der Entwicklung, aber ich werde auch einige Ergebnisse seiner Lösung nennen.

Schritt 1. Suchen Sie nach dem Bereich mit Fenstern

Die Grundidee ist, dass eine Reihe identischer Objekte (wie Fenster), die in einem Haus in einer Reihe identischer Objekte gut unterscheidbar sind, eine periodische Folge von Pixelhelligkeit erzeugen. Dies ist genau die Reihenfolge, die gefunden werden muss. Nachfolgend sind die Hauptstufen des Algorithmus aufgeführt.

Zuerst übersetzen wir das Bild in Graustufen und skalieren es (ich habe Bilder mit einer Größe von 400 x 600 Pixel verwendet).

Abb. 1 Original s / w-Bild

Weiter in der Schleife:

1. Auswahl auf dem Bild eines relativ schmalen (40px) Streifens auf die gesamte Höhe (Abb. 2, unteres Bild ohne Punkte)
2. Mittelung der Helligkeit über die Breite des Streifens. Es zeigt sich die Linie w der Verteilung der gemittelten Helligkeit über die Höhe des Hauses (Abb. 2, obere Grafik). Es hat eine deutlich sichtbare periodische Struktur, die für den Bereich charakteristisch ist, in dem sich Fenster befinden. Fenster im Schatten sind weniger unterscheidbar, aber das tut nicht weh.
3. Die Differenz dw der um den Abstand sh verschobenen Werte von w und w wird berechnet. Das Suchverfahren verwendet einen solchen Verschiebungswert sh, um die maximale Verringerung des Medians der Differenzen dw zu erreichen (Fig. 2, untere Grafik).
   
   
   Abb.2 "Fensterstreifen"

Es reicht jedoch nicht aus, das Bildband zu finden, auf dem der Median am stärksten reduziert wurde. Tatsache ist, dass Bereiche mit viel Grün oder Himmel mit kleinen Scherwerten eine größere Abnahme bewirken können als Fenster. Wenn wir jedoch die Abhängigkeit des Medianwerts vom Verschiebungswert für Streifen mit und ohne Fenster darstellen, können wir einen wesentlichen Unterschied feststellen: Bei Verschiebungswerten nahe der Höhe der Böden weist das Diagramm mit Fenstern deutlich sichtbare Extrema auf. Daher ist es nicht erforderlich, das absolut erreichbare Niveau des Medians zu messen, sondern dessen maximale Abnahme vom Maximum während der Schichtzunahme für jedes Fenster. Dies ist ein wichtiger Punkt.

ohne Fenster	mit Fenstern

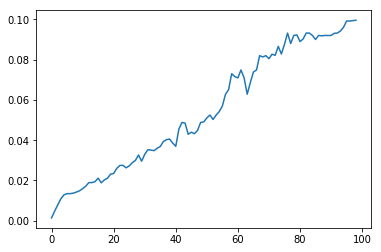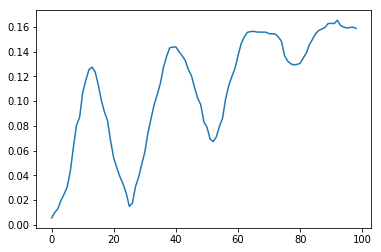Abb. 3 Änderung des Medians der gemittelten Helligkeit mit zunehmender Verschiebung

Unten ist Python3-Code mit Kommentaren.

image = Image.open("raf_data/32.jpg").resize((600,400)) # . img = np.array(image.convert("L"), dtype=float)/255 SEARCH_WIDTH = 40 #    x_opt = [0, 1] #    :      sh_range = range(1,100) #    kmax = 0 #       for x in range(0, img.shape[1]-SEARCH_WIDTH, int(SEARCH_WIDTH/2)): amax = 0 amin = 1 #      for sh in sh_range: #    w = img[:,x:x+SEARCH_WIDTH].mean(axis=1) aim = (pd.DataFrame(w)-pd.DataFrame(w).shift(sh))[sh:].abs().median().values[0] #    aim    sh if aim>amax: amax = aim amin = amax if aim<amin: amin = aim aim_k = amax/amin if aim_k>kmax: x_opt = [x, sh, w] kmax = aim_k print(' : {0},  : {1}'.format(x_opt[0], x_opt[1])) 

Fig. 2 markiert die Punkte, die im Abstand der gefundenen Verschiebung eingestellt sind. Wie Sie sehen können, markieren sie jedes Fenster gut. Das heißt, Wir kennen bereits die Höhe des Bodens!
Der betrachtete Algorithmus findet gute regelmäßige Zonen an den Fassaden verschiedener Wohngebäude (Abb. 4).



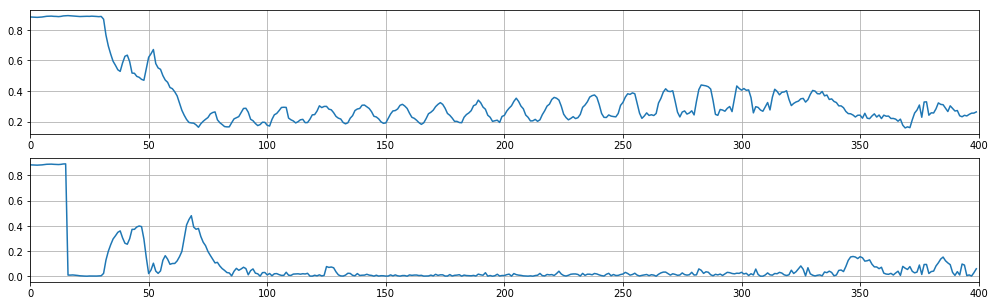
Abb. 4 Beispiel

Schritt 2. Zählen der Anzahl der Stockwerke

In diesem Schritt beginnen die Hauptschwierigkeiten. Weitere Aktionen können wie folgt sein:

1. Schätzen Sie die Höhe des Hauses, indem Sie die Kurve der Unterschiede der durchschnittlichen Helligkeit analysieren oder maschinelles Lernen anwenden. Teilen Sie die Höhe des Hauses durch die Höhe des Bodens und erhalten Sie die Anzahl der Stockwerke.
2. Suchen Sie im Fenster des ersten Schritts nach Objekten, die Fenstern ähnlich sind, und zählen Sie sie direkt, z. B. an bestimmten Punkten.

Es erscheint natürlich, zuerst die erste Methode auszuprobieren: Sobald die Höhe der Böden bekannt ist, muss die Höhe des Hauses bestimmt werden. Schemata, die den in Schritt 1 gezeigten ähnlich sind, erweisen sich jedoch unter Berücksichtigung aller möglichen Grenzen und Übergänge als schlecht geeignet, um die Höhe des Hauses zu bestimmen. In einigen Fällen ist es möglich, gute Arbeitsbeispiele zu erhalten, aber für ein konstant gutes Ergebnis sind Ansätze mit maschinellem Lernen erforderlich.

Abb. 5 Bestimmen der Höhe des Hauses anhand eines zufälligen Waldes