Eines der Hightech-Elemente der modernen Luft- und Raumfahrt sowie der Militärindustrie sind hochpräzise Trägheitsnavigationssysteme (ANNs). Die Aufgabe solcher Systeme, die auf Beschleunigungsmessern und optischen Gyroskopen basieren, besteht darin, die Winkelgeschwindigkeiten, Beschleunigungen eines sich bewegenden Objekts und die Gesamtorientierung des Objekts im dreidimensionalen Raum zu bestimmen.

Die Besonderheiten der ANN-Modellierung bestehen darin, dass im Bereich der Modellierung häufig sowohl geradlinige als auch rotatorische Bewegungen auftreten, die den Betrieb dieser Systeme stark beeinflussen und dementsprechend berücksichtigt werden müssen. In unserem Artikel werden wir kurz darauf eingehen, was der Sagnac-Effekt ist und wie darauf basierende Geräte im COMSOL Multiphysics ^® -Paket numerisch untersucht werden können.

Zur bequemen Navigation geben wir zu Beginn einen kurzen Überblick über den Artikel:

1. Was sind optische Gyroskope?
2. Die Besonderheiten der Berücksichtigung der Rotation in der Simulation
3. Sagnac-Effekt: theoretische Grundlage
4. Sagnac-Interferometermodell in COMSOL Multiphysics ^®
5. Fazit

Optische Gyroskope und der Sagnac-Effekt

Vielleicht ist es das klassische Sagnac-Interferometer, das die Notwendigkeit einer hochpräzisen Registrierung der nicht trägen Bewegung der Simulationsdomäne am besten demonstriert.

Das einfachste Sagnac-Interferometer besteht aus folgenden Komponenten:

• Lichtquelle
• Ein Strahlteiler, der das Licht einer Quelle auf zwei verschiedenen Wegen lenkt und diese dann kombiniert
• Eine Reihe von Spiegeln (normalerweise mit zwei oder drei Spiegeln)

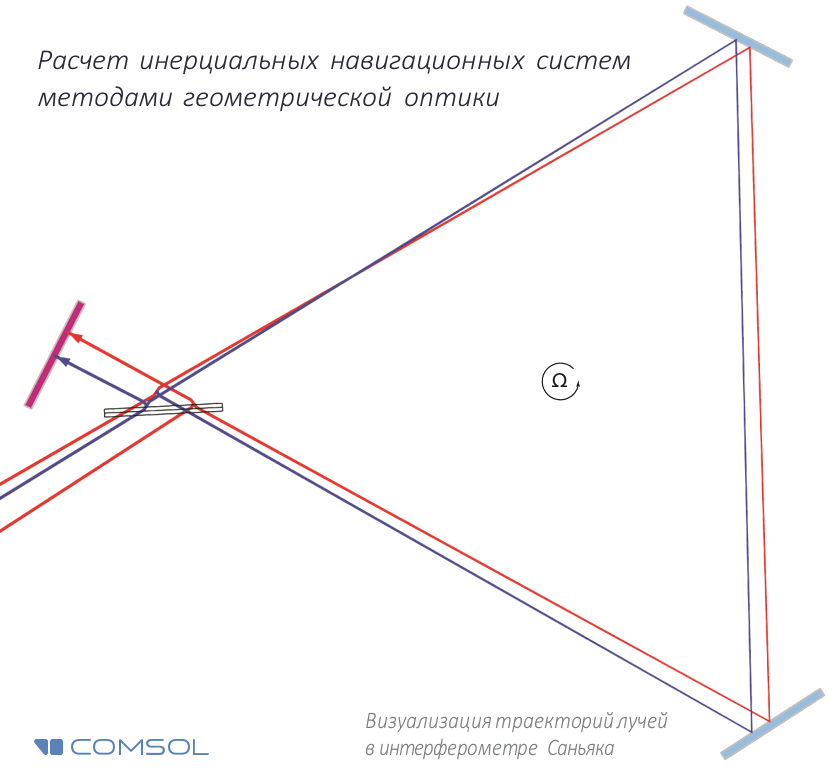
Der Strahlteiler und die Spiegel bilden eine dreieckige oder rechteckige Flugbahn, entlang der sich Licht in beide Richtungen ausbreitet. Zu diesem Zeitpunkt dreht sich auch das Navigationssystem selbst (sowie das Flugzeug oder Raumfahrzeug, in dem es installiert ist) mit einer bestimmten Winkelgeschwindigkeit. Durch Beobachtung der Interferenz von Lichtstrahlen (aufgrund des Sagnac-Effekts), die sich entlang dieser Trajektorien ausbreiten, ist es möglich, die Winkelgeschwindigkeit des Systems mit sehr hoher Genauigkeit zu bestimmen.

Die Messung kleiner Rotationen ist entscheidend für die Bestimmung und Steuerung der Ausrichtung von Objekten in der modernen Verteidigungs- und Raumfahrtindustrie. Derzeit werden am häufigsten Ringlaser und faseroptische Gyroskope verwendet, deren Prinzip auch auf dem Sagnac-Effekt basiert. Beachten Sie, dass ein Ringlasergyroskop sehr genau, billig und leicht zu warten ist, da es im Gegensatz zu mechanischen Gyroskopen keine rotierenden Teile enthält.

Modellierung der Lichtausbreitung in rotierenden optischen Bauteilen

Wie berechnet man den Weg der Lichtausbreitung in einem rotierenden System aus Spiegeln, Prismen und Strahlteilern? Um nicht in die Relativitätstheorie einzutauchen, nehmen wir an, dass die Rotationsgeschwindigkeit viel geringer ist als die Lichtgeschwindigkeit, aber groß genug, dass wir die Rotation berücksichtigen müssen. Es gibt mindestens zwei Ansätze zur Lösung dieses Problems:

1. Schreiben Sie Gleichungen für die Ausbreitung von Licht in einem nicht trägen Referenzrahmen um
2. Drehen Sie die Struktur in Echtzeit, wenn Sie Strahlen ausbreiten

Der Unterschied zwischen diesen Ansätzen besteht darin, dass sich das Modell in einem Fall in einem nicht trägen Referenzrahmen befindet, der mit einem sich bewegenden Interferometer verbunden ist (Option Nr. 1), oder in einem im Raum fixierten „Labor“ -Referenzsystem (Option Nr. 2). Da die zweite Option viel einfacher zu implementieren ist, werden wir diesen Ansatz verwenden, um das Sagnac-Interferometer zu simulieren.

Das COMSOL Multiphysics ^® -Paket ist sehr effektiv für die Modellierung von Geräten mit einer sich bewegenden oder deformierenden Struktur (einschließlich des Sagnac-Interferometers und eines Ringlasergyroskops) und ermöglicht die Integration und Simulation verschiedener interdisziplinärer physikalischer Prozesse in einem einzigen Rechenmodell.

Die Analyse verformbarer und sich bewegender Strukturen wird traditionell mit besonderer Sorgfalt durchgeführt, da sie in verschiedenen Bereichen eingesetzt wird: bei der Analyse der thermischen Beanspruchung, der Wechselwirkung eines Fluids mit einer Struktur, bei Mehrphasenströmungen sowie beim Galvanisieren, bei piezoelektrischen Bauelementen usw. Tatsächlich reicht es für eine genaue Strahlverfolgung in einer sich bewegenden Struktur aus, die Winkelgeschwindigkeit des Systems anzuzeigen und dann eine Standardberechnung auf der Grundlage geometrischer Optiktechnologien zu starten.

Sagnac-Effekt: theoretische Grundlage

Bevor wir mit der Beschreibung des im Paket implementierten Modells fortfahren, wollen wir kurz untersuchen, was der Sagnac-Effekt ist.

Stellen Sie sich vor, das Licht bewegt sich streng um einen Kreis (z. B. entlang eines Glasfaserkabels) in zwei entgegengesetzten Richtungen, wie in Abb. 2 dargestellt. 1. Strahltriggerpunkt - $$$P_0$. Die gestrichelte Linie zeigt die Richtung im Uhrzeigersinn an, und die dicke durchgezogene Linie zeigt die Richtung gegen den Uhrzeigersinn an. Lichtstrahlen in dieser Einstellung sind gegenläufig zueinander, da sie sich in entgegengesetzten Richtungen über den Umfang ausbreiten.

Wenn der Ring bewegungslos wäre, würden sich die Strahlengänge zweimal schneiden: zuerst am gegenüberliegenden Punkt des Kreises und dann am Startpunkt $$$P_0$. Stellen Sie sich nun vor, der Ring dreht sich mit einer bestimmten Winkelgeschwindigkeit gegen den Uhrzeigersinn um seine Mitte. Wenn wir der Bewegung des Punktes folgen $$$P_0$Während der Ausbreitung des Lichts werden wir sehen, dass ein Strahl, der sich im Uhrzeigersinn ausbreitet, zu ihm zurückkehrt, wenn er sich bereits in einer neuen Position befindet. $$$P_1$. Wann auf den Punkt $$$P_0$Ein Strahl, der sich gegen den Uhrzeigersinn ausbreitet, kehrt zurück, bewegt sich weiter und ist in Position $$$P_2$. $$$P_2$in größerer Entfernung von $$$P_0$als $$$P_1$weil sich der Kreis auch gegen den Uhrzeigersinn dreht.

Abb. 1. Lichtausbreitung im Uhrzeigersinn und gegen den Uhrzeigersinn entlang der Kante eines rotierenden Kreises.

Offensichtlich ist die Darstellung in Fig. 1 zur Klarheit deutlich skaliert, und in Wirklichkeit ist der Abstand zwischen den Punkten 10 Milliarden Mal kleiner. Selbst in diesem Fall führt die Differenz des zurückgelegten optischen Weges jedoch zu einer Phasenverschiebung und dementsprechend zu Interferenzen.

Ohne auf theoretische Berechnungen einzugehen (aber wenn sie interessant sind, empfehlen wir die folgende klassische Arbeit von Post, Evert J. "Sagnac-Effekt", Reviews of Modern Physics, 39, Nr. 2, S. 475, 1967 ), die endgültige Beziehung zwischen der Winkelgeschwindigkeit $$$\ Omega$und der Unterschied im optischen Weg $$$\ Delta L$kann ausgedrückt werden als:

$$

$$\ Delta L = {{4 \ Omega A} \ über {c_0}}$$

Wo $$$A$Ist die Fläche des betrachteten Kreises und $$$c_0$Ist die Lichtgeschwindigkeit.

Im Allgemeinen ist der Sagnac-Effekt noch allgemeiner als das oben beschriebene Beispiel. Der Ausbreitungsweg zweier entgegenkommender Strahlen kann eine beliebige Form haben, aber die Verzögerung zwischen ihnen ist immer proportional zur Größe des Bereichs, der durch die Kontur begrenzt ist, in der sich die Strahlen ausbreiten. Darüber hinaus wird dieser Effekt auch in Fällen beobachtet, in denen das Rotationszentrum nicht mit dem Zentrum der Kontur übereinstimmt.

Testmodell eines Sagnac-Interferometers basierend auf optischer Strahlverfolgung

Um zu überprüfen, wie COMSOL Multiphysics ^® berechnet wird $$$\ Delta L$und daher betrachten wir die Empfindlichkeit des Geräts als Testdesign des Sagnac-Interferometers, bei dem sich das Licht nicht um den Umfang, sondern entlang des Umfangs des Dreiecks ausbreitet, an dessen Oberseite sich zwei Spiegel und ein Strahlteiler befinden (Abb. 2).

Abb. 2. Schema des Sagnac-Interferometers.

Der Anfangsstrahl durchläuft einen Strahlteiler, wodurch zwei Strahlen gleicher Intensität gebildet werden. Zum Zeitpunkt des Austritts aus dem Strahlteiler befinden sie sich am gleichen Punkt und haben die gleiche Phase. Da sich das Spiegelsystem dreht, unterscheiden sich ihre optischen Wege (und daher Phasen) voneinander, wenn die Strahlen zum Strahlteiler zurückkehren.

In der Praxis statt kleiner Mengen $$$\ Delta L$Systeme erkennen häufig eine Frequenzverschiebung (oder Schwebungsfrequenz) $$$\ Delta \ nu$::

$$

$${{\ \ Delta \ nu} \ over {\ nu}} = {{\ Delta L} \ over {L}}$$

Hier $$$L$Ist die effektive Länge der Kontur, entlang der sich die Strahlen ausbreiten, und $$$\ nu$- ihre Häufigkeit. Bitte beachten Sie das $$$\ Delta L$direkt in der Berechnung ermittelt.

Der Prozess der numerischen Strahlverfolgung kann leicht automatisiert werden, beispielsweise zur Durchführung einer parametrischen Analyse. In Abb. Abbildung 3 zeigt die Ergebnisse der parametrischen Analyse in einem weiten Bereich von Winkelgeschwindigkeitswerten von relativ klein bis sehr groß.

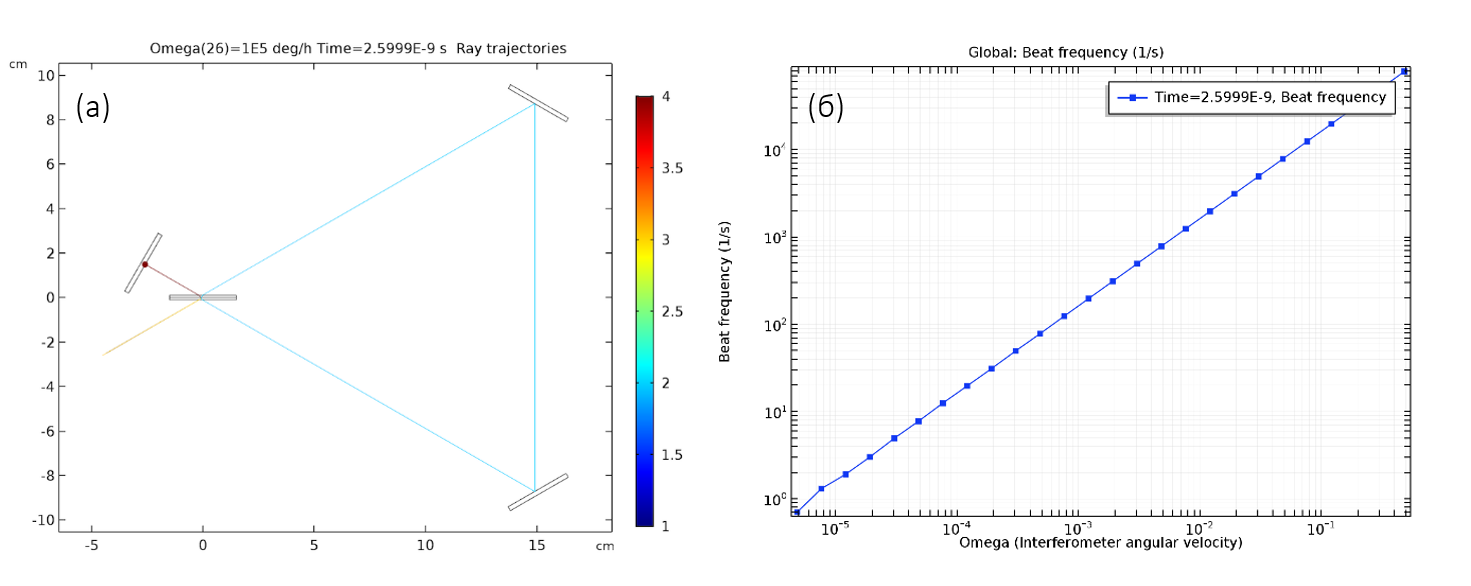
Abb. 3. (a) Strahlengänge in einem Testinterferometer. Die Abweichungen in der Flugbahn der beiden Strahlen sind so unbedeutend, dass sie selbst in Nahaufnahme nicht erkennbar sind. (B) Die Abhängigkeit der Schwebungsfrequenz von der Winkelfrequenz der Rotation des Systems.

Die entsprechende Schwebungsfrequenz stimmt hervorragend mit den theoretischen Werten überein. Durch Ändern des Abstands zwischen den Spiegeln kann gezeigt werden, dass die Steigung dieser Linie proportional zur Fläche des dreieckigen Bereichs ist, der zwischen den einfallenden Strahlen eingeschlossen ist.

Ein Blick in die Zukunft oder die praktische Anwendung der numerischen Modellierung optischer Gyroskope

Die obigen Ergebnisse zeigen, dass es durch Verfolgen von Strahlen in einer rotierenden Geometrie (Rahmen) unter Verwendung des beschriebenen Verfahrens möglich ist, die Empfindlichkeit von Vorrichtungen basierend auf dem Sagnac-Effekt mit hoher Genauigkeit zu berechnen, wenn die Rotationsgeschwindigkeit im Vergleich zur Lichtgeschwindigkeit niedrig ist (d. H. Ohne relativistische Effekte). Dank dieses neuen Modells verfügen Modellierungsspezialisten und Ingenieure, die mit Winkelorientierungssystemen arbeiten, nun über eine vorgefertigte Arbeitsvorlage zur Untersuchung des Sagnac-Effekts, der dem Betrieb von Ringlasergyroskopen zugrunde liegt.

Ein aufmerksamer Leser wird wahrscheinlich nach der Notwendigkeit einer solchen numerischen Simulation fragen, da der Sagnac-Effekt durch die obige Formel genau beschrieben wird. Es ist zu bedenken, dass echte ANNs viel komplizierter sind als der einfachste Aufbau mit einem Strahlteiler und zwei Spiegeln, der oben diskutiert wurde. Solche Systeme werden zusammen mit anderen empfindlichen Geräten auf engstem Raum installiert, ein zusätzlicher Rahmen ist erforderlich, der die Unbeweglichkeit der optischen Komponenten relativ zueinander gewährleistet. Darüber hinaus arbeiten ANNs häufig in aggressiven Umgebungen und werden durch mechanische Beanspruchung, Temperatur und elektromagnetische Felder beeinflusst. Diese Faktoren beeinflussen das Verhalten und die Empfindlichkeit des Gyroskops, was eine detailliertere und gründlichere Betrachtung erfordert und nicht mit derselben einfachen Formel beschrieben werden kann.

Daher ist die im Sagnac-Interferometer oder in einem Ringlasergyroskop dargestellte Strahlverfolgung nur der erste Schritt in einer hochpräzisen und umfassenden multiphysikalischen Analyse großer optischer Systeme. COMSOL Multiphysics ^® ermöglicht die Strahlverfolgung unter realistischsten Bedingungen, insbesondere unter Berücksichtigung der Erwärmung und der thermischen Verformung optischer Komponenten, was neue Möglichkeiten für ein besseres Verständnis und eine bessere Bewertung der Empfindlichkeit und Genauigkeit komplexer Trägheitsnavigationssysteme eröffnet.

Weitere Informationen

Dieses Material basiert auf folgenden Artikeln:

• C. Boucher. Verständnis des Sagnac-Effekts durch Strahloptiksimulation , Laser Focus World, August 2018
• Simulation eines Sagnac-Interferometers und eines Ringlaserkreisels mit geometrischen Optikmethoden, Unternehmensblog COMSOL

Für eine detailliertere Kenntnis der beschriebenen Methoden und Beispiele können Sie in den Kommentaren oder über den Link eine kostenlose, voll funktionsfähige Demoversion von COMSOL Multiphysics ^® anfordern.

Wir laden auch alle am 1. November zum Hauptereignis für aktuelle und zukünftige COMSOL-Benutzer ein - dem COMSOL-Tag in Moskau .