Kompromiss bestanden - Sie können heiraten!

Einführung

Die Finite-Elemente-Methode (FEM oder FEM, die sie im Ausland haben) ist fest in der Praxis technischer Berechnungen beim Entwurf komplexer Systeme verankert. Dies betrifft weitgehend Festigkeitsberechnungen der Mechanik. Die Anwendung dieser Methode, die von der entsprechenden Software implementiert wird, verkürzt den Entwicklungszyklus des Endgeräts erheblich und eliminiert die Masse an experimentellen Überprüfungen, die bei Verwendung klassischer Berechnungen auf der Grundlage der Methoden des Sopromat und der Strukturmechanik erforderlich sind. Bis heute wurde eine Menge Anwendungssoftware entwickelt, die FEM implementiert. An vorderster Front steht das leistungsstarke ANSYS an den Seiten und in ehrenamtlicher Entfernung - CAD-Systeme mit integriertem FEM-Modul (SolidWorks, Siemens NX, Creo Parametric, Compass 3D).

CalculiX ist stark, aber schwierig und unverständlich. Werden wir das beheben?



Natürlich ist die FEM in den Bildungsbereich eingedrungen - um sie für reale Aufgaben einsetzen zu können, müssen relevante Fachkräfte geschult werden. In Hauptstädten, an großen technischen Universitäten, ist die Situation in diesem Bereich mehr oder weniger normal, und in unserer Region wird das gleiche ANSYS beispielsweise am Department of Elasticity Theory der Southern Federal University verwendet. Aber an der Peripherie, an eng spezialisierten und nicht reichen Universitäten, ist die Situation bedauerlich. Und es ist ganz einfach: ANSYS kostet ungefähr 2 Millionen Rubel für einen Arbeitsplatz, und es ist mehr als ein Platz erforderlich. Leider können es sich nicht alle Universitäten leisten, 30 bis 40 Millionen für die Organisation eines Computerkurses für den Unterricht in FEM zu zahlen.

Eine der Alternativen ist die Verwendung von freier Software im Bildungsprozess. Glücklicherweise ist eine solche Software verfügbar. Es gibt jedoch praktisch keine russischsprachigen Materialien zu seiner Verwendung. Um diese Situation zu korrigieren, werde ich diesen Artikel der Einführung von CalculiX widmen - einem offenen, kostenlosen Softwarepaket zur Lösung linearer und nichtlinearer dreidimensionaler Probleme der Mechanik eines festen verformbaren Körpers sowie der Fluid- und Gasmechanik mithilfe der Finite-Elemente-Methode.

1. Was ist CalculiX und wo kann man es bekommen? Windows-Installation

Das CalculiX-Paket besteht aus einer Reihe von Konsolendienstprogrammen, darunter ein Präprozessor zum Aufbereiten von Quelldaten, ein FEM-Solver und ein Postprozessor zum Verarbeiten der Ergebnisse. CalculiX wird sowohl unabhängig als auch als Teil anderer Produkte verwendet, unter denen FreeCAD an Dynamik gewinnt. Eine andere Frage ist, dass CalculiX in unserem Land noch wenig bekannt ist, was direkt durch den einzigen Artikel über diese Ressource angegeben wird .

Ich werde speziell das folgende Material in Bezug auf die Arbeit in Windows als das am häufigsten verwendete und verwendete Material einschließlich Bildungseinrichtungen angeben. Darüber hinaus ist die Verwendung vieler kostenloser Programme ein offener Schmerz.

Wenn Sie das Windows-Paket von der offiziellen CalculiX-Website übernehmen, wird völlig unklar, was als Nächstes zu tun ist. In Verbindung mit der englischsprachigen Dokumentation macht es diesem Produkt für viele ein Ende und führt dann zu giftigen Kommentaren über die Unmöglichkeit seiner Verwendung. Und zum Teil ist dies wahr - die Eintrittsschwelle ist wirklich hoch. Aber wir werden es trotzdem versuchen.

Es gibt eine Reihe inoffizieller, relativ unerfahrener Builds dieses Wunders für Windows, darunter bConverged CalculiX für Windows . Wir laden das Distributionskit von hier herunter, entpacken es und installieren es mit der Standardmethode "weiter, weiter ...". Die Installation stellt daher kein besonderes Rätsel dar und ist für einen unerfahrenen Benutzer durchaus zugänglich. Als Hauptarbeitsumgebung verwendet dieses Paket den SciTE-Texteditor, der Aufrufe von CalculiX-Komponenten sowie die Möglichkeit der interaktiven Eingabe von Befehlen integriert, und es sieht ungefähr so ​​aus (anklickbar).

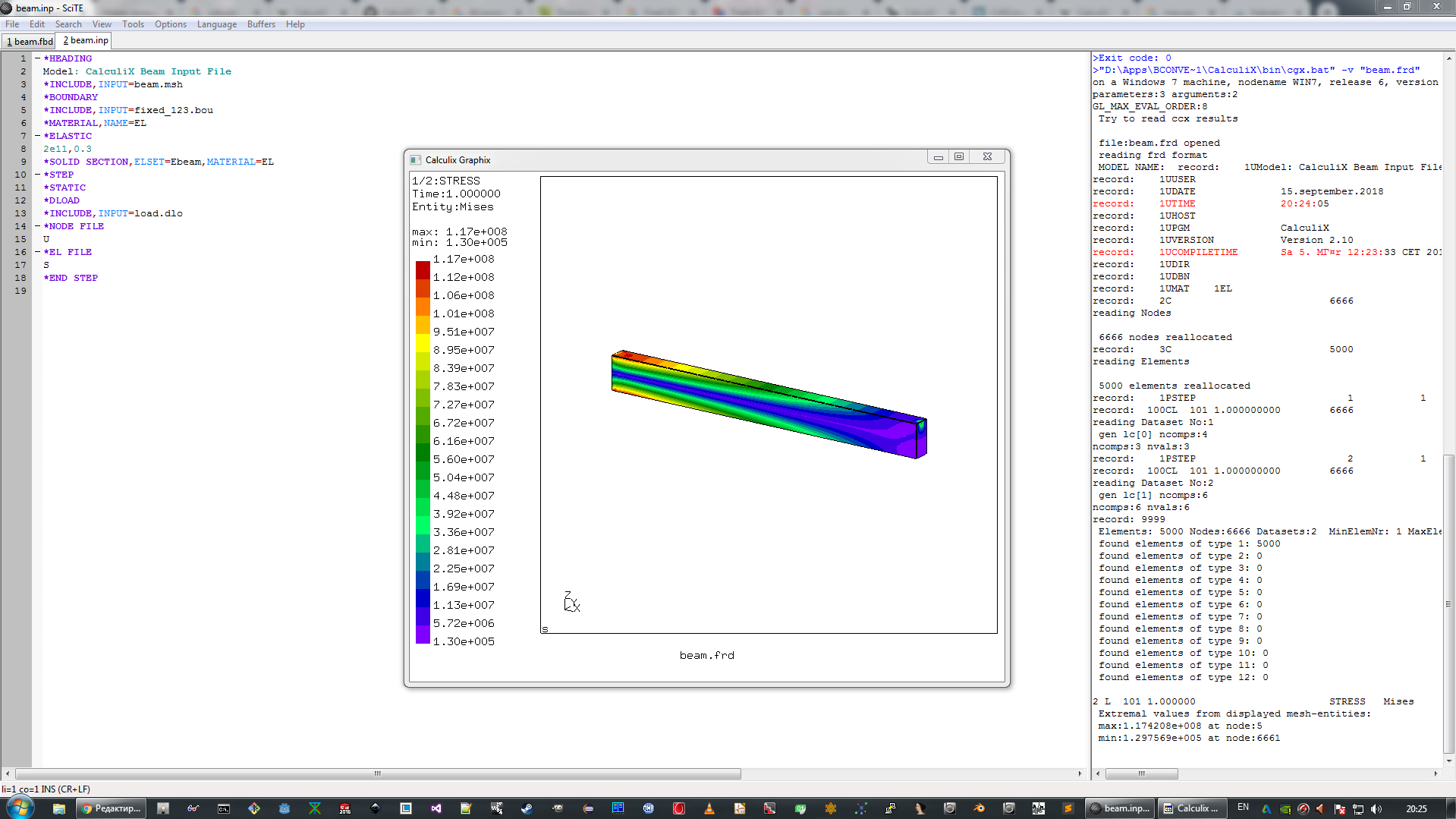
2. Das Problem der Balkenbiegung und ihre analytische Lösung mit Sopromat-Methoden

Nehmen Sie ein einfaches Schülerproblem - das Biegen eines Stahlträgers, dessen eines Ende eingeklemmt ist, und die vertikale Kraft F, die auf das andere ausgeübt wird .



Die Parameter des Problems sind wie folgt: F = 10 kN; l = 1 m ist die Länge des Strahls; h = 0,1 m und b = 0,05 m sind die Abmessungen des Querschnitts. Der Einfachheit halber wird das Eigengewicht des Trägers nicht berücksichtigt, da es mit einem Trägergewicht von 39 kg deutlich geringer ist als die aufgebrachte Last. Wir finden die maximale Normalspannung im Balkenabschnitt und berechnen auch die Balkenauslenkung aufgrund von Biegeverformungen.

Jeder Schüler, der keinen Kompromiss übersprungen hat, kann ein solches Problem leicht lösen. Um die edlen Dons nicht in Verlegenheit zu bringen, werde ich alle Details der Entscheidung in einen Spoiler packen


Für diejenigen, die zu faul sind, um unter den Spoiler zu schauen, gebe ich sofort die Antwort auf das Problem: die maximale normale Spannung im Strahlabschnitt $$$\ sigma_x = 119$MPa und die maximale Auslenkung beträgt 3,97 mm. Diese Zahlen werden zum späteren Vergleich mit dem Verfahren zur Lösung dieses Problems in CalculiX angegeben.

3. Vorbereitung der Geometrie und des Rechengitters

Zunächst müssen Sie geometrische Daten zu dem betreffenden Teil in CalculiX eingeben. Ja, es ist möglich, Geometrie aus CADs zu exportieren, wie dies in demselben ANSYS der Fall ist, aber wir werden die Folter durchlaufen und die Geometrie manuell eingeben. Öffnen Sie den SciTE-Editor aus dem bConverged-Kit und geben Sie den folgenden Text ein

pnt p1 0 0 0
pnt p2 0.25 0 0
pnt p3 0.5 0 0
pnt p4 0.75 0 0
pnt p5 1.0 0 0

Speichern Sie die Datei unter dem Namen Beam.fbd und drücken Sie F10, um die Vorverarbeitung zu starten. Wir werden so etwas wie das Folgende sehen



Der Befehl pnt erstellt einen Punkt im Raum mit den angegebenen Koordinaten und hat folgende Syntax

pnt [ ] [x] [y] [z]

Verbinden Sie diese Punkte nun mit Linien und fügen Sie der Datei den folgenden Text hinzu

line l1 p1 p2 25
line l2 p2 p3 25
line l3 p3 p4 25
line l4 p4 p5 25

nachdem Sie nach Drücken von F10 das folgende Bild erhalten haben



Das Team

line [ ] [ 1] [ 2] [ ]

Erstellt eine Linie, die die darin angegebenen Punkte verbindet, und fügt Zwischenpunkte hinzu, die die Linie in eine bestimmte Anzahl von Segmenten unterteilen (in unserem Fall 25 für jede Linie). Dies wird später für die Netzgenerierung nützlich sein. Jetzt mach die Finte mit unseren Ohren

seta lines l l1 l2 l3 l4
swep lines sweeplines tra 0 0 0.1 10

Erstes Team

seta [ ] [ 1] ... [ N]

kombiniert mehrere Objekte zu einem Set mit dem angegebenen Namen. In der Tat ist dies ein Analogon zur Gruppierung von Objekten. Nächster Befehl

swep [ ] [ ] [ ] [, ] []

Verschiebt den ausgewählten Satz von Objekten, um einen neuen Satz zu bilden. Bewegliche Objekte werden kopiert. In diesem Fall bildet die Bewegung von Punkten Linien, die Bewegung von Linien - Flächen, die Bewegung von Flächen - kontinuierliche Volumina. In unserem Fall verschieben wir den Satz von Linienlinien entlang der Z-Achse um 0,1 Meter, während die resultierenden Linien in 10 Segmente unterteilt sind. Wir drücken F10 ... ähm, und was ist das?



Ghm, ein leerer Bildschirm ... Es ist einfach zu beheben, fügen Sie einfach Zeilen am Ende des Skripts hinzu

plot pa all
plus la all

Diese Befehle weisen Sie an, alle Punkte (pa) zu zeichnen und alle Linien (la) zur Anzeige hinzuzufügen. Danach erhalten wir dieses Ergebnis



Erstellen wir nun Oberflächen basierend auf den von uns erstellten Linien

seta surfaces s A001 A002 A003 A004

Hinzufügen der Anzeige dieser Oberflächen ganz am Ende des Skripts

plus sa all




Jetzt werden wir eine weitere Verschiebung durchführen, jetzt entlang der Y-Achse um 0,05 Meter, wobei alle Linien entwickelt werden, die durch die Verschiebung um 5 Segmente gebildet werden.

swep surfaces swepsurface tra 0.0 0.05 0.0 5

Holen Sie sich etwas im Geist



Das resultierende Bild kann gedreht werden, indem Sie die linke Maustaste gedrückt halten und die Anzeige von Punkten und Linien entfernen. Wir werden etwas Verständliches sehen



Ja ... CalculiX ist weit entfernt von den üblichen visuellen Konzepten, die dem Massenbenutzer vertraut sind, aber wir haben trotzdem die Geometrie unseres Strahls erstellt.

Geometrie, Geometrie, aber für die Netzgenerierung machen wir den nächsten Schritt - entfernen Sie alle Plot- und Plus-Befehle und wickeln Sie den Code für die Geometriegenerierung wie folgt in seto- und setc-Befehle ein

seto beam
pnt p1 0 0 0
pnt p2 0.25 0 0
pnt p3 0.5 0 0
pnt p4 0.75 0 0
pnt p5 1.0 0 0
line l1 p1 p2 25
line l2 p2 p3 25
line l3 p3 p4 25
line l4 p4 p5 25
seta lines l l1 l2 l3 l4
swep lines sweeplines tra 0 0 0.1 10
seta surfaces s A001 A002 A003 A004
swep surfaces swepsurface tra 0 0.05 0 5
setc beam

Dieses Befehlspaar kombiniert die gesamte erstellte Geometrie zu einem bestimmten Geometrieblock mit dem Namensstrahl. Jetzt kann diese geometrische Gruppe durch die Netzgenerierung übersprungen werden, wobei der obige Befehlscode angegeben wird

elty beam he8
mesh beam

- Erzeugt ein Gitter aus Parallelepipeds (he8) basierend auf einer Geometrie namens Strahl. Drucken Sie nun das generierte Netz in eine Datei

send beam abq

- Mesh-Ausgabe in eine Datei mit dem Namenbeam.msh im Format des ABAQUS FEM-Pakets (es gibt ein solches proprietäres Paket von FEM-Berechnungen und CalculiX versteht sein Format).



Wenn das Raster generiert wird, können Sie in die Datei Beam.msh schauen und dort so etwas sehen

*NODE, NSET=Nbeam
1,0.000000000000e+000,0.000000000000e+000,1.000000000000e-001
2,0.000000000000e+000,0.000000000000e+000,9.000000000000e-002
3,0.000000000000e+000,1.000000000000e-002,9.000000000000e-002
4,0.000000000000e+000,1.000000000000e-002,1.000000000000e-001
5,1.000000000000e-002,0.000000000000e+000,1.000000000000e-001
6,1.000000000000e-002,0.000000000000e+000,9.000000000000e-002
7,1.000000000000e-002,1.000000000000e-002,9.000000000000e-002
8,1.000000000000e-002,1.000000000000e-002,1.000000000000e-001
9,0.000000000000e+000,2.000000000000e-002,9.000000000000e-002
10,0.000000000000e+000,2.000000000000e-002,1.000000000000e-001
11,1.000000000000e-002,2.000000000000e-002,9.000000000000e-002
.
.
.
.
*ELEMENT, TYPE=C3D8, ELSET=Ebeam
1, 1, 2, 3, 4, 5, 6, 7, 8
2, 4, 3, 9, 10, 8, 7, 11, 12
3, 10, 9, 13, 14, 12, 11, 15, 16
4, 14, 13, 17, 18, 16, 15, 19, 20
5, 18, 17, 21, 22, 20, 19, 23, 24
6, 5, 6, 7, 8, 25, 26, 27, 28
7, 8, 7, 11, 12, 28, 27, 29, 30
8, 12, 11, 15, 16, 30, 29, 31, 32
9, 16, 15, 19, 20, 32, 31, 33, 34

Anscheinend ist dies eine Liste von Eckpunkten der Gitterelemente mit ihren Koordinaten, gefolgt von einer Liste von Flächen. Um das Ganze schöner aussehen zu lassen, verwenden wir den interaktiven Modus CalculiX. Geben Sie dazu die folgenden Befehle nacheinander ein, und lassen Sie das Grafikfenster aktiv

plot f beam

- Alle Flächen der Geometrie anzeigen

view edge off

- Schalten Sie die Kantenanzeige aus

view elem

- Schalten Sie die Anzeige der Rasterelemente ein. Wir vervollständigen die Eingabe jedes Befehls durch Drücken der Eingabetaste. Die eingegebenen Befehle werden wie folgt im SciTE-Fenster unten rechts angezeigt



Ja, Sie können es nicht als sehr praktisch bezeichnen, aber wir erhalten trotzdem ein Bild des generierten Netzes.



Ich stelle fest, dass alle Zwischenpunkte, die beim Erstellen der Geometrie erstellt wurden, zu Netzknoten wurden. So haben wir ein hexagonales Gitter mit 100 x 10 x 5 Knoten und einer Elementkantengröße von 10 mm erhalten. Die von uns erstellte Dateibeam.fbd beschreibt die Geometrie des Problems und den Prozess der Erstellung des Netzes.

4. Grenzen setzen

Ein wichtiger Schritt bei der Anwendung der FEM besteht darin, Beschränkungen für die Bewegung von Strukturpunkten festzulegen, dh die ihr auferlegten Beschränkungen zu berücksichtigen. In unserem Fall ist eines der Enden des Trägers eingeklemmt, und es kann angenommen werden, dass eines seiner Enden vollständig stationär ist. Wir müssen dem Löser mitteilen, welche Knoten des FE-Netzes bewegungslos sind. Wir drücken F10, wenn die Datei Beam.fbd geöffnet ist, und warten, bis das Fenster mit dem Bild des Strahls angezeigt wird



Geben Sie im interaktiven Modus den Befehl ein
rot -y
plot n beam

Das erste Team setzt das Modell so ein, dass die Y-Achse von uns wegschaut, das zweite - enthält Zeichnungsknoten (n) des FE-Netzes. Wenn Sie das Modell bewegen (die rechte Maustaste gedrückt halten) und das Bild skalieren (das Mausrad gedrückt halten), erhalten Sie dieses Bild



Jetzt müssen wir alle Knoten auswählen, die wir als fest definieren möchten. Dazu verwenden wir wieder den interaktiven Dateneingabemodus. Wir rekrutieren ein Team

qadd fixed

Dadurch wird eine Reihe von Knoten erstellt, die als fest bezeichnet werden. Der Cursor im Grafikfenster wechselt in den Elementauswahlmodus - er wird in Form eines Pfeils mit einem kleinen Quadrat angezeigt. Setzen Sie den Cursor so



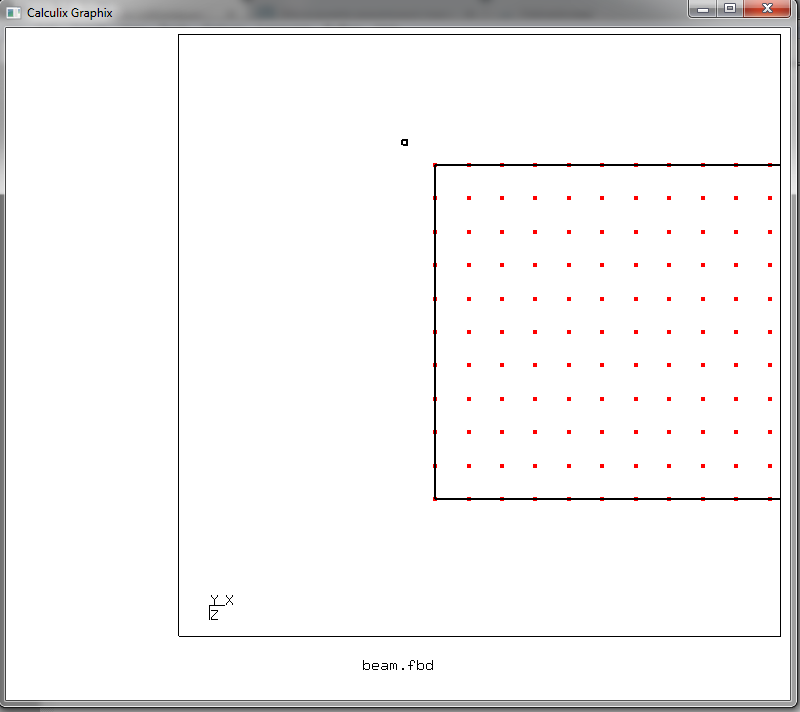
und drücken Sie die Taste r. Und dann setzen wir den Cursor so



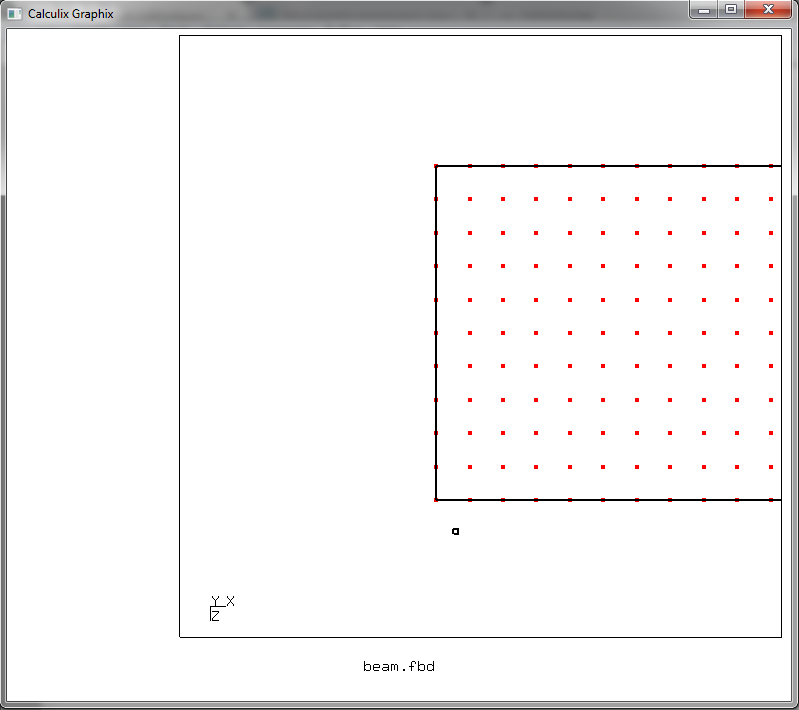
und drücken Sie erneut r. So haben wir einen Auswahlbereich mit rechteckiger Form gebildet, dessen Diagonale durch die Cursorpositionen festgelegt wird, die durch Drücken von r markiert sind. Mit diesem Rechteck wählen wir die Knoten aus, die am Ende des Balkens liegen müssen



Drücken Sie a und dann n, um die markierten Knoten hervorzuheben. Im Konsolenfenster wird ein Fußtuch mit einer Liste ausgewählter Knoten angezeigt (das Bild kann angeklickt werden).



Geben Sie q ein, um den Auswahlmodus und den Befehl zu verlassen

plus n fixed g

um die Knoten der festen Gruppe in grün (g) anzuzeigen. Jetzt können wir sehen, welche Knoten in der Pinning-Bedingung enthalten sind.



Jetzt müssen wir diese Knoten als Einschränkungsdatei entladen, die anschließend der Eingabe des Lösers zugeführt wird. Geben Sie dazu den Befehl ein

send fixed abq spc 123

- Entladen einer Gruppe fester Knoten in Form einer Einschränkungsdatei im ABAQUS-Format (abq), wodurch die Bewegung aller Gruppenknoten in allen drei Freiheitsgraden (1-X-Achse, 2-Y-Achse, 3-Z-Achse) eingeschränkt wird. Als Ergebnis wird die Datei fixed_123.bou mit dem folgenden Inhalt gebildet

** BOUNDARY based on fixed
1, 1, ,
2, 1, ,
3, 1, ,
4, 1, ,
9, 1, ,
10, 1, ,
13, 1, ,
14, 1, ,
17, 1, ,
.
.
.


- Tatsächlich ist dies eine Aufzählung aller Knoten und der Freiheitsgradzahl, um die die Bewegung eines bestimmten Knotens begrenzt ist.

5. Lastverteilung

Nachdem wir unseren Balken gesichert haben, werden wir versuchen, ihn zu laden. Schalten Sie die Anzeige von Gesichtern und Elementen wieder ein

plot f beam
view edge off
view elem

Richten Sie das Bild so aus, dass wir den oberen Teil des losen Strahlendes sehen können



Wechseln wir in den Objektauswahlmodus

qadd load

Platzieren Sie den Cursor auf der gewünschten Fläche und drücken Sie f



Das Gesicht wird lila hervorgehoben, und im Konsolenfenster wird eine Beschreibung angezeigt, die dem Lastsatz hinzugefügt wird.

qadd load
2541 e:3873 s:6 n= 5298 5310 5312 5300

Drücken Sie a, um die Bildung des Sets zu beenden, und q, um den Auswahlmodus zu verlassen. Wir üben einen Druck auf die ausgewählte Fläche aus, der eine resultierende Kraft von 10.000 N ergibt. Es ist leicht zu berechnen, dass die Fläche der ausgewählten Fläche 1 cm ² beträgt, was bedeutet, dass der gewünschte Druck 10 ⁸ Pa beträgt. Stellen Sie diese Last mit dem Befehl ein

send load abq pres 1e8

- Zeigt die Last in der Datei load.dlo im ABAQUS-Format an. Die Datei sieht so aus

** Pressure based on load
3873, P6, 100000000.000000

Die Nummer des Netzelements, seine Fläche und der Druckwert auf dieser Fläche werden angezeigt. Somit kann die Aufbereitung der Anfangsdaten als abgeschlossen betrachtet werden.

6. Beschreibung der Eingabedaten und Start des Solvers

Alle diese Daten - das Raster, die Einschränkungen und die Lasten - sollten jetzt auf die Eingabe des FEM-Lösers gezogen werden, für den wir eine Eingabedatei dieser Art bilden

beam.inp
*HEADING
Model: CalculiX Beam Input File for Habrahabr article
*INCLUDE,INPUT=beam.msh
*BOUNDARY
*INCLUDE,INPUT=fixed_123.bou
*MATERIAL,NAME=EL
*ELASTIC
2e11,0.3
*SOLID SECTION,ELSET=Ebeam,MATERIAL=EL
*STEP
*STATIC
*DLOAD
*INCLUDE,INPUT=load.dlo
*NODE FILE
U
*EL FILE
S
*END STEP


Ich werde genauer erklären, was was ist. Erster Abschnitt der Datei

*HEADING
Model: CalculiX Beam Input File for Habrahabr article
*INCLUDE,INPUT=beam.msh

Legt die Beschreibung der Aufgabe fest und enthält eine Datei mit dem CE-Mesh Beam.msh. Der nächste Abschnitt bildet die Randbedingungen - die Beziehungen, die wir in der Datei fixed_123.bou definiert haben

*BOUNDARY
*INCLUDE,INPUT=fixed_123.bou


Wir sollten nicht vergessen, welches Material wir als elastisch eingestellt haben, um den Elastizitätsmodul und das Poisson-Verhältnis zu bestimmen. Wir nehmen die Durchschnittswerte für Baustähle

*MATERIAL,NAME=EL
*ELASTIC
2e11,0.3
*SOLID SECTION,ELSET=Ebeam,MATERIAL=EL

Im letzten Abschnitt wird der Aufgabentyp festgelegt - die Berechnung der statischen Belastung und der Belastungen aus der Datei load.dlo

*STEP
*STATIC
*DLOAD
*INCLUDE,INPUT=load.dlo
*NODE FILE
U
*EL FILE
S
*END STEP


Nachdem Sie überprüft haben, ob in SciTE eine Registerkarte mit der Datei Beam.inp vorhanden ist, drücken Sie Strg + F10, um den Solver zu starten. Wir bekommen einen Auspuff, der uns sagt, dass CalculiX dort etwas für uns berechnet hat. Auspuff, um den Text, den ich unter den Spoiler bringe, nicht zu überladen

7. Nachbearbeitung und Entscheidungsanalyse

Die vom Löser erhaltenen Ergebnisse müssen vom Postprozessor verarbeitet werden. Um es aufzurufen, drücken Sie Umschalt + F10 und Sie erhalten ein Grafikfenster mit dem Bild des Strahls. Klicken Sie auf die linke Seite dieses Fensters außerhalb des Rahmens mit dem Bild des Strahls und rufen Sie das Menü auf



Was interessiert uns? Spannungen in Balkenabschnitten - wählen Sie Datensätze -> STRESS. Das Menü wird ausgeblendet, aber wir rufen es erneut auf und wählen Datensätze -> Entitäten -> Mises. Infolgedessen wird der von Mises-Äquivalentspannungsmodus eingeschaltet.



Also - der Moment der Wahrheit! Die maximale äquivalente Spannung im Trägerabschnitt beträgt 117 MPa, was sich geringfügig vom Ergebnis des Kompromisses unterscheidet. Aber! Bei der Lösung des Sopromatproblems haben wir die Tangentialspannungen beim Biegen und Scheren nicht berücksichtigt, sondern nur die Normalspannungen aus dem Biegen berechnet. Was passiert mit der Auslenkung? Gehen Sie zum Menü: Datensätze -> DISP und Datensätze -> Entitäten -> D3



Wir beobachten, dass die maximale Verschiebung dem belasteten Ende des Trägers entspricht und 3,96 Millimeter beträgt! Großartig und korreliert mit unserer Berechnung unter Verwendung des Mohr-Integrals.

Durch einfache Manipulationen, über die hier gelesen werden kann , wird auch eine Animation von Strahlverformungen erzeugt.

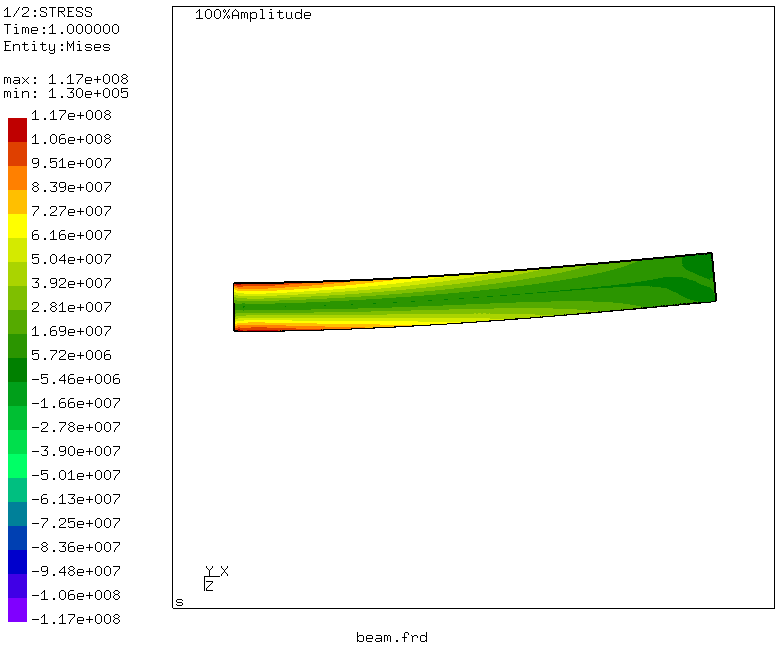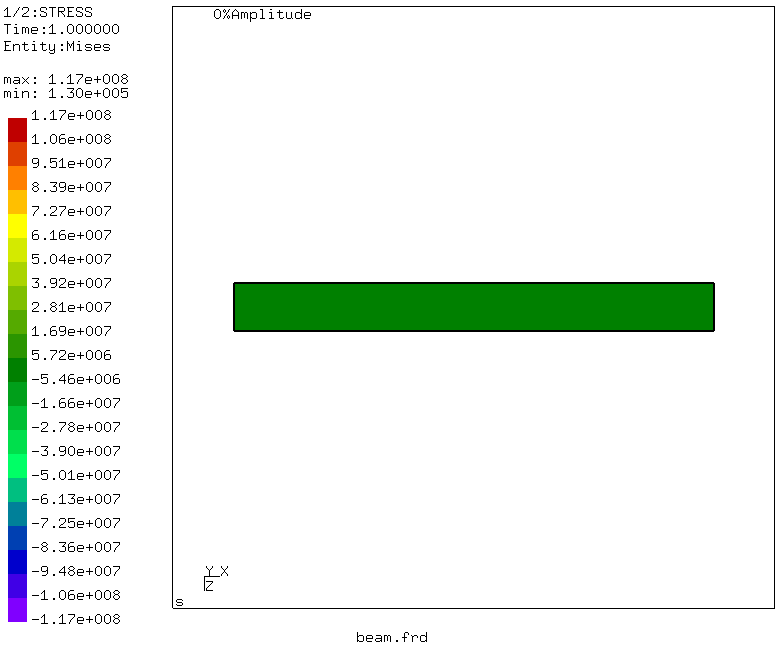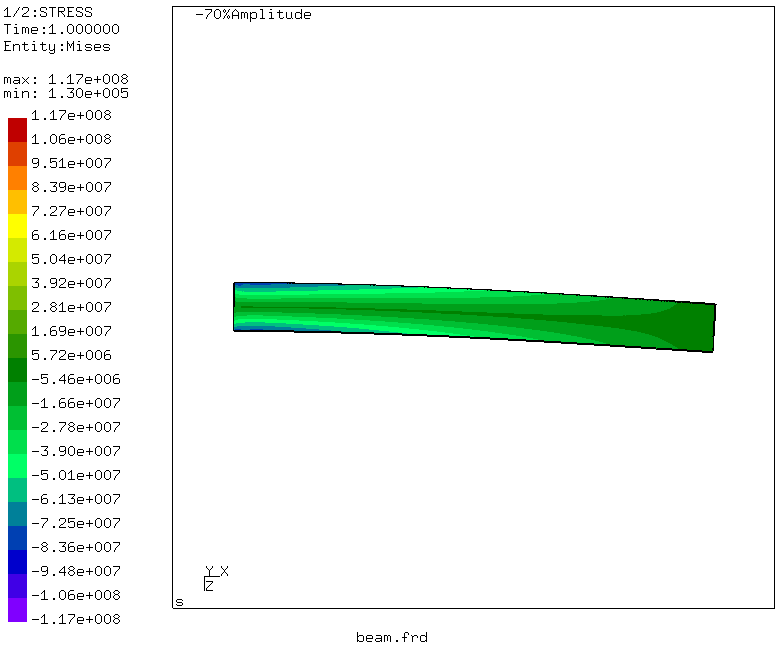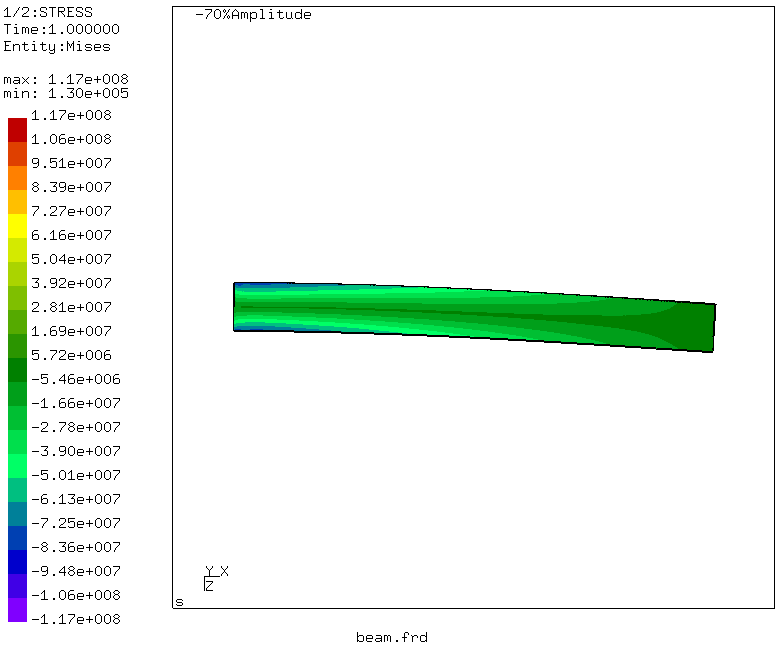
Schlussfolgerungen ziehen

"Äh, Alter, warte eine Minute, was kommt als nächstes ?!" Hmm, der Mensch kann nicht in einen Artikel die ganze Vielfalt der Probleme einpassen, die auftreten, wenn die FEM im Allgemeinen und CalculiX im Besonderen erwähnt werden. Der Artikel erwies sich als umfangreich und ziemlich langweilig. Und sein Zweck ist es, zwei Dinge in einer verständlichen Sprache zu erklären:

1. Open Source wurde von der FEM-Analysesoftware nicht bestanden
2. Das Studium und die Verwendung dieser Software ist nicht so schwierig, wie es auf den ersten Blick erscheinen mag

Genug für einen Übersichtsartikel? Ich denke ja. Bei der Erstellung des Artikels wurden folgende Quellen verwendet:

1. Calculix FEA Beam - diente als Grundlage für das gesamte vorgestellte Material. Da die Erfahrungen des Autors hier hinzugefügt werden und der gesamte Code von ihm während des Schreibens des Artikels geschrieben wurde, handelt es sich nicht um eine Übersetzung, sondern um ein Tutorial in russischer Sprache
2. Offizielles CalculiX-Handbuch

Beispielcode ist auf Gitlab verfügbar .

Abschließend stelle ich fest - ich bin nicht stark, ich hatte keinen Kompromiss an der Universität. Wenig später zwang mich das Leben (und die Liebe!), Die Grundlagen zu kennen. Vielleicht sind also Fehler im Text vorhanden, über die ich auf böswillige Kommentare warte, und ich verspreche, alle Kommentare zu berücksichtigen.

Danke für die Aufmerksamkeit!