Schnellste Gleitkommazahlen im Wilden Westen

Bei der Implementierung eines „Lesers“ trat ein Problem mit einer erhöhten Genauigkeit der Berechnungen auf. Der Berechnungsalgorithmus arbeitete schnell mit Standard-Gleitkommazahlen, aber als Bibliotheken für genaue Berechnungen verbunden wurden, begann sich alles wild zu verlangsamen. In diesem Artikel werden Algorithmen zum Erweitern von Gleitkommazahlen unter Verwendung eines Mehrkomponentenansatzes betrachtet, aufgrund dessen eine Beschleunigung erreicht werden konnte, da die Gleitkomma-Arithmetik auf einem CP-Chip implementiert ist. Dieser Ansatz ist nützlich für eine genauere Berechnung der numerischen Ableitung, der Matrixinversion, des Polygontrimmens oder anderer geometrischer Probleme. So ist es möglich, 64-Bit-Float auf Grafikkarten zu emulieren, die diese nicht unterstützen.

Einführung

Da Nikluas Wirth uns hinterlassen hat, die Nummern 0 und 1 zu behalten, speichern wir sie darin. Und leben Menschen im Dezimalsystem, und die scheinbar gewöhnlichen Zahlen 0,1 und 0,3 sind im Binärsystem nicht durch einen endlichen Bruchteil darstellbar? Wir erleben einen kulturellen Schock, wenn wir Berechnungen an ihnen anstellen. Natürlich wird versucht, Bibliotheken für Prozessoren basierend auf dem Dezimalsystem zu erstellen, und IEEE hat sogar standardisierte Formate.

Im Moment berücksichtigen wir jedoch überall den binären Speicher und führen alle Geldberechnungen mit Bibliotheken für genaue Berechnungen durch, z. B. Bignumber, was zu Leistungseinbußen führt. Asiks betrachten Krypto, und in Prozessoren gibt es so wenig Platz für Ihre Dezimalarithmetik, sagen Vermarkter. Daher ist ein Mehrkomponentenansatz, wenn eine Zahl in Form einer nicht transformierten Summe von Zahlen gespeichert wird, ein praktischer Trick und eine sich aktiv entwickelnde Sphäre auf dem Gebiet der theoretischen Informatik. Obwohl Decker 1971 immer noch lernte, ohne Genauigkeitsverlust korrekt zu multiplizieren, erschienen gebrauchsfertige Bibliotheken viel später (MPFR, QD) und nicht in allen Sprachen, anscheinend da nicht alle IEEE-Standards unterstützten, sondern zum Beispiel auch später strenge Beweise für Berechnungsfehler im Jahr 2017 für Doppelwortarithmetik.

Doppelwortarithmetik

Was ist der Punkt? In bärtigen Zeiten, als es keine Standards für schwebende Zahlen gab, kam Møller auf die Idee, um Probleme bei der Implementierung der Rundung zu vermeiden, und Knuth bewies später, dass es eine fehlerfreie Summierung gibt. Laufen auf diese Weise

function quickTwoSum(a, b) { let s = a + b; let z = s - a; let e = b - z; return [s, e]; } 

In diesem Algorithmus wurde angenommen, dass wenn $$$| a | > | b |$dann kann ihre genaue Summe als die Summe zweier Zahlen dargestellt werden $$$s + e$und Sie können sie paarweise für nachfolgende Berechnungen speichern, und die Subtraktion wird auf die Addition mit einer negativen Zahl reduziert.



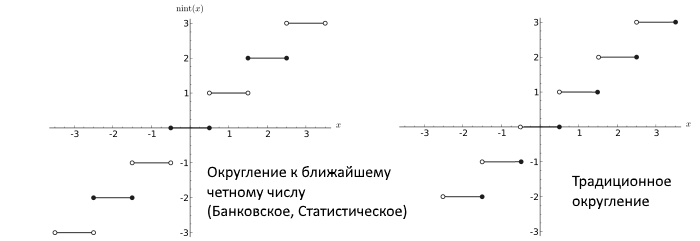
In der Folge zeigte Dekker, dass bei Verwendung von Gleitkommazahlen, bei denen auf die nächste gerade Zahl gerundet wird (Rundung auf die nächste gerade Zahl, was im Allgemeinen ein korrektes Verfahren ist, das bei langen Berechnungen und dem IEEE-Standard nicht zu großen Fehlern führt), dann gibt es einen fehlerfreien Multiplikationsalgorithmus.

 function twoMult(a, b) { let A = split(a); let B = split(b); let r1 = a * b; let t1 = -r1 + A[0] * B[0]; let t2 = t1 + A[0] * B[1]; let t3 = t2 + A[1] * B[0]; return [r1, t3 + A[1] * B[1]]; } 

Dabei ist split () der Algorithmus von Herrn Weltkamp zum Teilen einer Zahl

 let splitter = Math.pow(2, 27) + 1; function split(a) { let t = splitter * a; let d = a - t; let xh = t + d; let xl = a - xh; return [xh, xl]; } 

mit Konstante $$$C = 2 ^ s + 1$Dies entspricht etwas mehr als der Hälfte der Länge der Mantisse, was beim Multiplikationsprozess nicht zu einem Überlaufen von Zahlen führt und die Mantisse in zwei Hälften teilt. Beispielsweise beträgt bei einer Wortlänge von 64 Bit die Länge der Mantisse 53 und dann s = 27.



Auf diese Weise lieferte Dekker den fast vollständigen Satz, der für die Berechnung in Doppelwortarithmetik benötigt wird. Seitdem wurde auch angegeben, wie man zwei Doppelwortzahlen multipliziert, dividiert und quadriert.

Sein quickTwoSum-Algorithmus zum Summieren von zwei Doppelwörtern war überall „inline“, und die Prüfung wurde verwendet $$$| a | > | b |$. Auf modernen Prozessoren, wie in [4] beschrieben, ist es billiger, zusätzliche Operationen mit Zahlen zu verwenden, als den Algorithmus zu verzweigen. Daher ist der folgende Algorithmus jetzt besser geeignet, um zwei Einzelwortnummern hinzuzufügen

 function twoSum(a, b) { let s = a + b; let a1 = s - b; let b1 = s - a1; let da = a - a1; let db = b - b1; return [s, da + db]; } 

Das ist also die Summe und Multiplikation von Doppelwortzahlen.

 function add22(X, Y) { let S = twoSum(X[0], Y[0]); let E = twoSum(X[1], Y[1]); let c = S[1] + E[0]; let V = quickTwoSum(S[0], c); let w = V[1] + E[1]; return quickTwoSum(V[0], w); } function mul22(X, Y) { let S = twoMult(X[0], Y[0]); S[1] += X[0] * Y[1] + X[1] * Y[0]; return quickTwoSum(S[0], S[1]); } 

Im Allgemeinen wird die vollständigste und genaueste Liste von Algorithmen für Doppelwortarithmetik, theoretische Fehlergrenzen und praktische Implementierung im Link [3] von 2017 beschrieben. Bei Interesse empfehle ich daher dringend, direkt dorthin zu fahren. Im Allgemeinen ist in [6] und in [5] ein Algorithmus für Vierfachwörter für eine Mehrkomponentenerweiterung beliebiger Länge angegeben. Nur dort wird nach jeder Operation der Renormierungsprozess verwendet, der für kleine Größen nicht immer optimal ist, und die Genauigkeit der Berechnungen in QD ist nicht genau definiert. Generell lohnt es sich natürlich, über die Grenzen der Anwendbarkeit dieser Ansätze nachzudenken.

Horrorgeschichten Javascript-a. Vergleich von decimal.js vs bignumber.js vs big.js.

So kam es, dass fast alle Bibliotheken für genaue Berechnungen in js von einer Person geschrieben wurden. Die Illusion der Wahl entsteht, obwohl sie fast alle gleich sind. Darüber hinaus wird in der Dokumentation nicht explizit angegeben, dass sich die Größe Ihrer Zahl ständig verdoppelt, wenn Sie Zahlen nach jeder Multiplikations- / Divisionsoperation nicht runden, und die Komplexität des Algorithmus in x3500 zu einer einfachen Größe werden kann. Ein Vergleich der Berechnungszeit könnte beispielsweise so aussehen, wenn Sie die Zahlen nicht gerundet hätten.



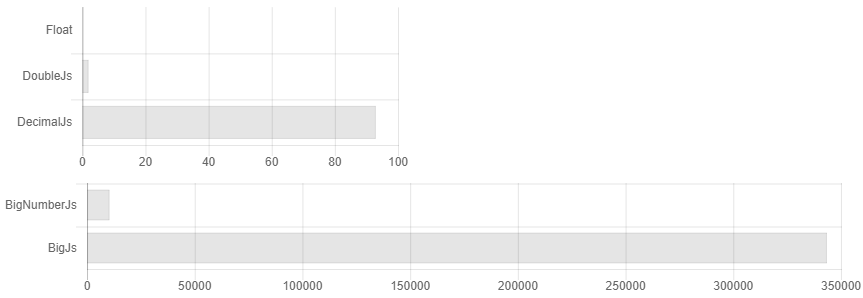
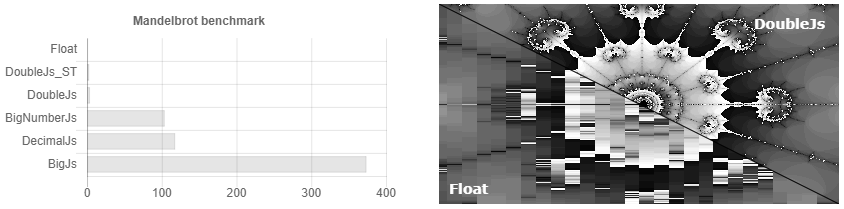
Das heißt, Sie setzen die Genauigkeit auf 32 Dezimalstellen und ... Ups, Sie haben bereits 64 Stellen, 128. Wir denken sehr genau! 256, 512 ... Aber ich habe 32 gesetzt! .. 1024, 2048 ... So etwas erscheint 3.500 Mal über dem Kopf. In der Dokumentation heißt es, dass bei wissenschaftlichen Berechnungen decimal.js wahrscheinlich besser für Sie ist. Wenn Sie jedoch nur regelmäßig abrunden, arbeitet Bignumber.js für wissenschaftliche Berechnungen etwas schneller (siehe Abb. 1). Wer muss die Hundertstel Cent zählen, wenn sie nicht als Wechselgeld ausgegeben werden können? Gibt es einen Fall, in dem ich mehr angegebene Nummern speichern muss und nicht mit ein paar zusätzlichen Zeichen aussteigen kann? Wie nimmt es den Sinus einer solchen Monsternummer, wenn niemand die strenge Genauigkeit der Konvergenz der Taylor-Reihe für beliebige Zahlen kennt? Im Allgemeinen gibt es keinen unbegründeten Verdacht, dass es möglich ist, die Berechnungsgeschwindigkeit dort zu erhöhen, indem beispielsweise Schönhage-Strassen-Multiplikationsalgorithmen verwendet und der Sinus mit Cordic-Berechnungen gefunden wird.

Double.js

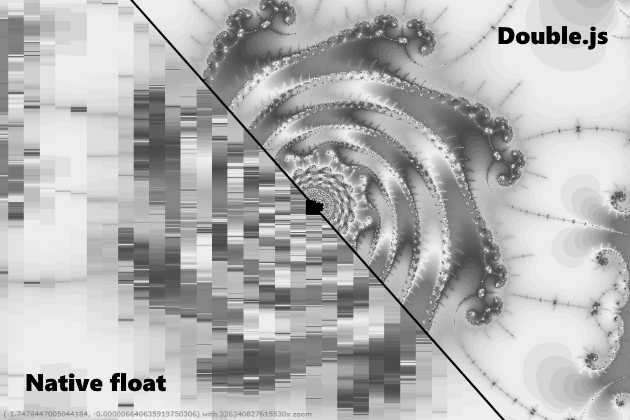
Ich möchte natürlich sagen, dass Double.js schnell und genau zählt. Dies ist jedoch nicht ganz richtig, das heißt, es ist zehnmal schneller, als es berücksichtigt, aber es ist nicht immer genau. Zum Beispiel kann 0.3-0.1 verarbeitet werden, indem es in einen doppelten Speicher übergeht und umgekehrt. Die Pi-Zahl kann jedoch mit einer doppelten Genauigkeit von fast 32 Stellen aufgelöst werden und funktioniert nicht zurück. Am 16. wird ein Fehler generiert, als ob ein Überlauf auftritt. Im Allgemeinen fordere ich die js-Community auf, zusammenzuarbeiten, um das Problem des Parsens zu lösen, da ich nicht weiterkomme. Ich habe versucht, digital zu analysieren und in doppelter Genauigkeit zu teilen, wie in QD, in Chargen von 16 Ziffern zu teilen und in doppelter Genauigkeit zu teilen, die Mantisse mit Big.js wie in einer der Julia-Bibliotheken zu teilen. Jetzt sündige ich an einem Fehler in .parseFloat (), da IEEE-Standards mit Rundung auf die nächste Ganzzahl auch mit ECMAScript 1 unterstützt werden. Natürlich können Sie versuchen, den Binärpuffer zu binden und alle 0 und 1 zu beobachten. Im Allgemeinen, wenn Sie dieses Problem lösen können, dann Es wird dann möglich sein, Berechnungen mit beliebiger Genauigkeit und Beschleunigung in x10-x20 aus bignumber.js durchzuführen. Bei vielen Mandelbrot wird jedoch bereits Qualität wiedergegeben, und Sie können es für geometrische Aufgaben verwenden.

Ein Jahr später kehrte ich hierher zurück und behebt immer noch ein Problem mit dem Parsen. Das Problem bestand nur in unzureichender Genauigkeit, wenn es mit 10 ^ (- n) multipliziert wurde. Alle Algorithmen wurden von Grund auf überarbeitet und laufen jetzt mit erschreckender Genauigkeit und Geschwindigkeit.



Hier ist ein Link zur Bibliothek , es gibt einen interaktiven Benchmark und eine Sandbox, in der Sie damit spielen können.

Verwendete Quellen

1. O. Møller. Quasi doppelte Genauigkeit in der Gleitkomma-Arithmetik. 1965.
2. Theodorus Dekker. Eine Gleitkomma-Technik zur Erweiterung der verfügbaren Präzision , 1971. [ Viewer ]
3. Mioara Joldes, Jean-Michel Müller, Valentina Popescu. Enge und strenge Fehlergrenzen für Grundbausteine ​​der Doppelwortarithmetik , 2017. [ PDF ]
4. Muller, J.-M. Brisebarre, N. de Dinechin usw. Handbuch der Gleitkomma-Arithmetik, Kapitel 14, 2010.
5. Jonathan Shewchuk. Robuste adaptive geometrische Gleitkomma-Prädikate , 1964. [ PDF ]
6. Yozo Hida, Xiaoye Li und David Bailey. Bibliothek für Double-Double- und Quad-Double-Arithmetik , 2000. [ PDF ]