Was zum Zeichnen von Vektorbildern? Für mich wie für viele andere ist die Antwort ziemlich offensichtlich: höchstwahrscheinlich im Illustrator. Gut oder in Inskape. Ich dachte auch, als mir befohlen wurde, achthundert Stücke für ein Physiklehrbuch zu zeichnen. Nichts dergleichen, nur technische Schwarz-Weiß-Illustrationen mit allerlei Blöcken, Kugeln, Federn, Linsen, Autos, Traktoren und dergleichen. Es wurde angenommen, dass das Buch in Latech verfasst sein würde, und ich erhielt Word-Dateien mit eingefügten Bildern - entweder in Bleistiftskizzen oder Scans aus anderen Büchern - und das Manuskript schien in irgendeiner Form zu sein. In diesem Fall erlag der erste Gedanke - Inscape zu zeichnen - Fantasien zum Thema "Wie würde es das alles automatisieren?". Aus irgendeinem Grund schien
MetaPost in diesem Moment die beste Option zu sein.
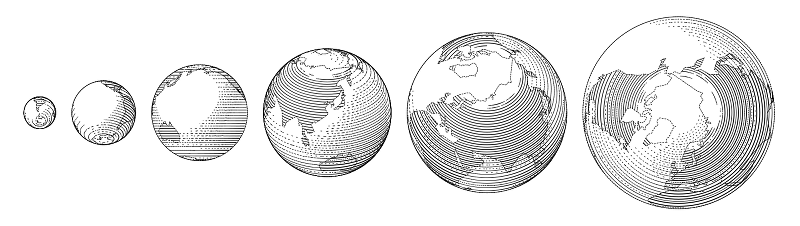
Das wichtigste Plus einer solchen Lösung ist, dass jedes Bild eine kleine Funktion mehrerer Variablen sein kann; Ein solches Bild lässt sich beispielsweise leicht in der Größe ändern und Streifen an bestimmte bisher unbekannte Umstände anpassen, ohne wichtige Proportionen zu verletzen, was mit herkömmlichen Mitteln nur schwer zu erreichen ist. Und die sich wiederholenden Elemente - die gleichen Kugeln und Federn - können so gestaltet werden, dass sie sich viel interessanter verhalten, als es die Mittel "menschlicher" Vektoreditoren erlauben.
Ich wollte Bilder mit Schraffur machen, wie man sie in alten Büchern findet.

Zuerst mussten wir Linien mit variabler Dicke bekommen. Die Hauptschwierigkeit besteht hier darin, eine Kurve zu konstruieren, die mehr oder weniger parallel zu der gegebenen ist, und bei Bedarf den Abstand zu der gegebenen zu ändern. Ich habe mich auf die wahrscheinlich primitivste
Art und
Weise verlassen, wie die Segmente, die die Zwischenpunkte der Bezier-Kurve verbinden, einfach in einem bestimmten Abstand parallel übertragen werden. Mit dem Unterschied, dass dieser Abstand entlang der Kurve variieren kann.
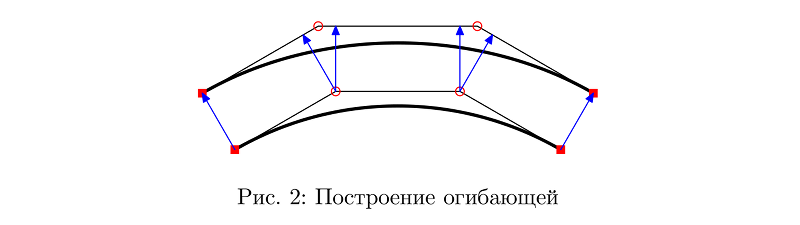
In den meisten Fällen ermöglicht dies ein anständiges Ergebnis.
BeispielcodeIm Folgenden wird davon ausgegangen, dass die Bibliothek
heruntergeladen wurde und sich irgendwo die
input fiziko.mp; befindet
input fiziko.mp; . Der schnellste Weg, um in ConTeXt zu starten und zu suchen (dann werden
beginfig und
endfig nicht benötigt):
\starttext
\startMPcode
input fiziko.mp;
\stopMPcode
\stoptext
oder in LuaLaTeX:
\documentclass{article}
\usepackage{luamplib}
\begin{document}
\begin{mplibcode}
input fiziko.mp;
\end{mplibcode}
\end{document}
beginfig(3);
path p, q; % , , ,
p := (0,-1/4cm){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 1/4cm);
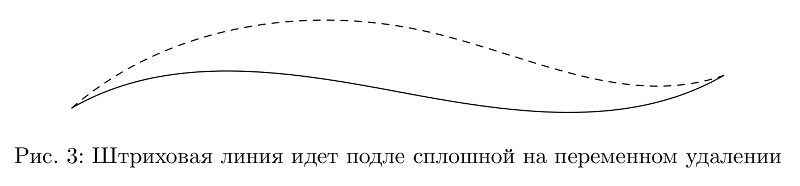
q := offsetPath(p)(1cm*sin(offsetPathLength*pi)); % — , — (offsetPathLength, 0 1), ,
draw p;
draw q dashed evenly;
endfig;
Nun können zwei dieser Kurven verwendet werden, um eine Kontur einer Linie variabler Dicke zu erstellen.

Beispielcodebeginfig(4);
path p, q[];
p := (0,-1/4cm){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 1/4cm);
q1 := offsetPath(p)(1/2pt*(sin(offsetPathLength*pi)**2)); %
q2 := offsetPath(p)(-1/2pt*(sin(offsetPathLength*pi)**2)); %
fill q1--reverse(q2)--cycle;
endfig;
Die Dicke sollte von unten etwas begrenzt sein, da das Raster sonst beim Drucken zu dünne Teile der Linien annimmt, was normalerweise nicht sehr schön ist. Eine Möglichkeit besteht darin, alle Linien, deren Dicke unter einem bestimmten Wert liegt, durch gestrichelte Linien mit derselben Mindestdicke zu zeichnen, sodass die Gesamtmenge an Farbe pro Längeneinheit im Durchschnitt der für die Linie mit der Zieldicke entspricht. Das heißt, anstatt die Farbmenge von den Seiten der Linie zu verringern, beginnen Sie, sie mit Querstreifen zu nagen.

Beispielcodebeginfig(5);
path p;
p := (0,-1/4cm){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 1/4cm);
draw brush(p)(1pt*(sin(offsetPathLength*pi)**2)); % , ,
endfig;
Jetzt können Sie Bälle zeichnen. Es können nur konzentrische Kreise sein, deren Dicke der Linien durch die Funktion der Beleuchtung der Kugel an den Punkten bestimmt wird, durch die die Linien verlaufen.
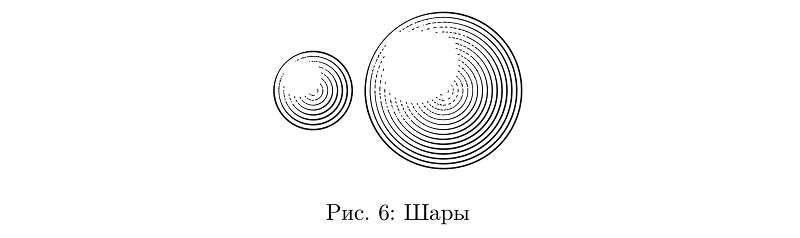
Beispielcodebeginfig(6);
draw sphere.c(1.2cm);
draw sphere.c(2.4cm) shifted (2cm, 0);
endfig;
Ein weiteres praktisches Grundelement sind „Schläuche“: grob gesagt Zylinder, die auf jede Weise gebogen werden können. Solange sie einen konstanten Querschnitt haben, ist bei ihnen alles einfach.
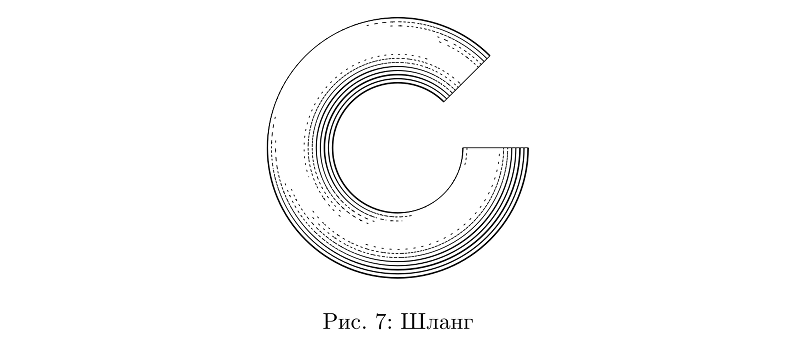
Beispielcodebeginfig(7);
path p;
p := subpath (1,8) of fullcircle scaled 3cm;
draw tube.l(p)(1/2cm); % — ,
endfig;
Wenn sich die Dicke ändert, muss die Anzahl der Striche entsprechend geändert werden, während die durchschnittliche Füllungsdichte unverändert bleibt, und auch Änderungen der Dicke bei der Berechnung der Beleuchtung berücksichtigt werden.
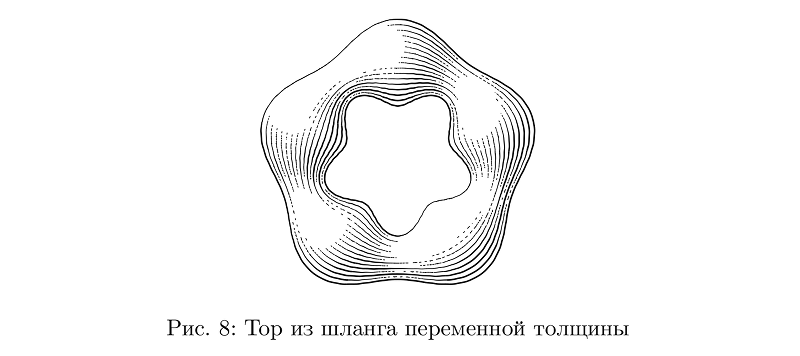
Beispielcodebeginfig(8);
path p;
p := pathSubdivide(fullcircle, 2) scaled 3cm;
draw tube.l(p)(1/2cm + 1/6cm*sin(offsetPathLength*10pi));
endfig;
Es gibt immer noch Schläuche mit Querschraffur, aber für sie war es schwieriger, das Problem der Beibehaltung der durchschnittlichen Füllungsdichte zu lösen, so dass sie in vielen Fällen immer noch nicht sehr gut aussehen.
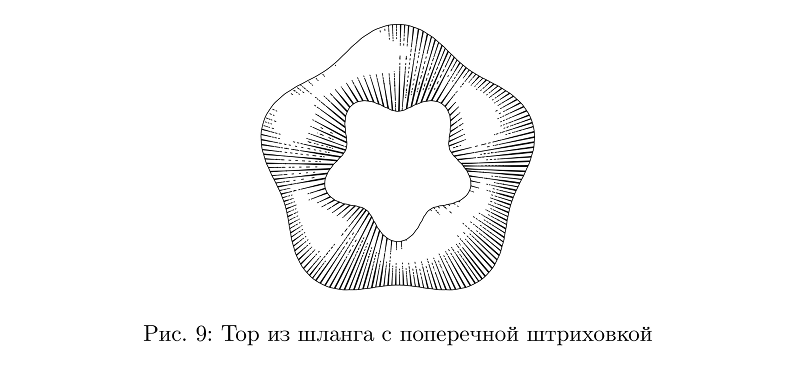
Beispielcodebeginfig(9);
path p;
p := pathSubdivide(fullcircle, 2) scaled 3cm;
draw tube.t(p)(1/2cm + 1/6cm*sin(offsetPathLength*10pi));
endfig;
Grundsätzlich kann vieles allein aus Schläuchen hergestellt werden: von Kegeln und Zylindern bis hin zu Balustern.
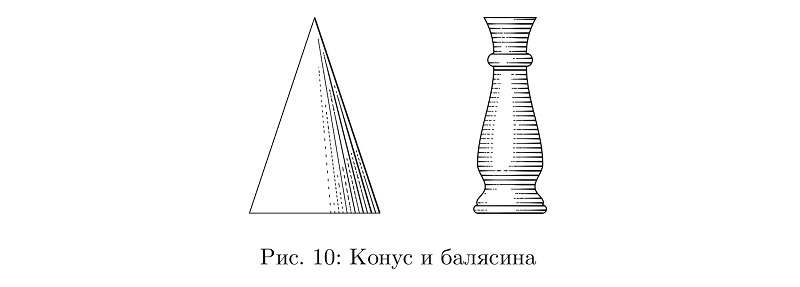
Beispielcodebeginfig(10);
draw tube.l ((0, 0) -- (0, 3cm))((1-offsetPathLength)*1cm) shifted (-3cm, 0); %
path p;
p := (-1/2cm, 0) {dir(175)} .. {dir(5)} (-1/2cm, 1/8cm) {dir(120)} .. (-2/5cm, 1/3cm) .. (-1/2cm, 3/4cm) {dir(90)} .. {dir(90)}(-1/4cm, 9/4cm){dir(175)} .. {dir(5)}(-1/4cm, 9/4cm + 1/5cm){dir(90)} .. (-2/5cm, 3cm); %
p := pathSubdivide(p, 6);
draw p -- reverse(p xscaled -1) -- cycle;
tubeGenerateAlt(p, p xscaled -1, p rotated -90); % , tube.t, — — , — .
endfig;
Einiges von dem, was aus solchen Teilen gebaut werden kann, befindet sich in der Bibliothek. Nehmen wir an, ein Globus ist im Grunde ein Ball.
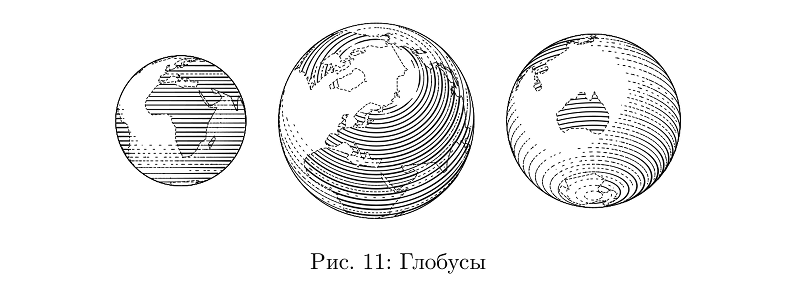
Beispielcodebeginfig(11);
draw globe(1cm, -15, 0) shifted (-6/2cm, 0); % , ,
draw globe(3/2cm, -30.28367, 59.93809);
draw globe(4/3cm, -140, -30) shifted (10/3cm, 0);
endfig;
Obwohl nicht: Hier verläuft die Schraffur parallel, und die Steuerung der Hubdicke zur Aufrechterhaltung der Füllungsdichte ist noch schwieriger als bei der Querschraffur an Schläuchen, sodass es sich um eine separate Art von Kugel handelt.
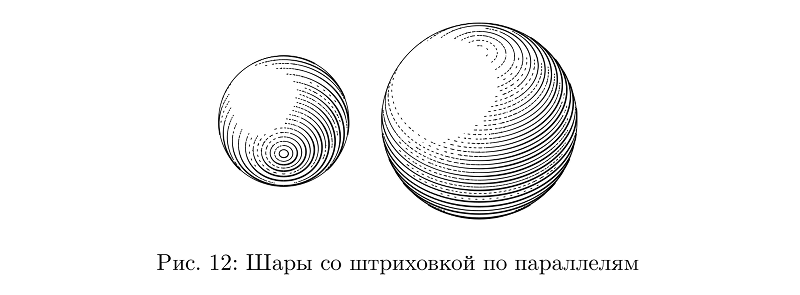
Beispielcodebeginfig(12);
draw sphere.l(2cm, -60); %
draw sphere.l(3cm, 45) shifted (3cm, 0);
endfig;
Und das Gewicht ist eine einfache Konstruktion von zwei Arten von Schläuchen mit variabler Dicke.
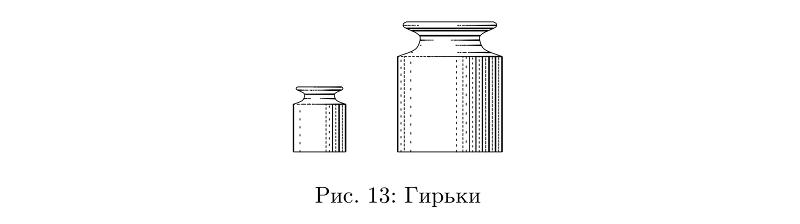
Beispielcodebeginfig(13);
draw weight.s(1cm); %
draw weight.s(2cm) shifted (2cm, 0);
endfig;
Es gibt noch ein Werkzeug, um die Schläuche in Knoten zu binden.
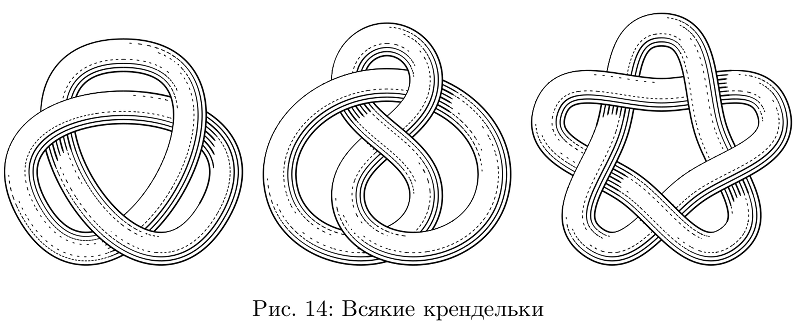
Beispielcode, um nicht zu überladen, nur ein Knotenbeginfig(14);
path p;
p := (dir(90)*4/3cm) {dir(0)} .. tension 3/2 ..(dir(90 + 120)*4/3cm){dir(90 + 30)} .. tension 3/2 ..(dir(90 - 120)*4/3cm){dir(-90 - 30)} .. tension 3/2 .. cycle;
p := p scaled 6/5;
addStrandToKnot (primeOne) (p, 1/4cm, "l", "1, -1, 1"); % primeOne , p 1/4cm, "l" ( tube.l, tube.t ) «» "1, -1, 1" p
draw knotFromStrands (primeOne); % .
endfig;
Die Schatten der Knoten sind einige Komplikationen im Beleuchtungsmodell. Im Prinzip stört es niemanden, sie in anderen Fällen zu verwenden, aber ich habe mir kein Ziel gesetzt, tief in die Lautstärke einzusteigen. Dies ist zwar nicht sehr praktisch, funktioniert aber nicht überall.
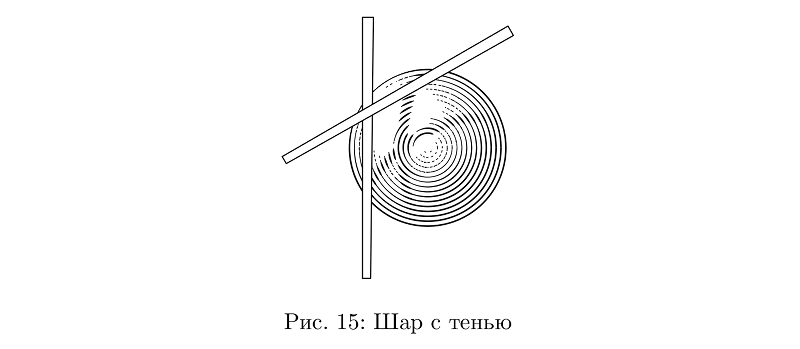
Beispielcodebeginfig(15);
path shadowPath[];
boolean shadowsEnabled;
numeric numberOfShadows;
shadowsEnabled := true; %
numberOfShadows := 1; %
shadowPath0 := (-1cm, -2cm) -- (-1cm, 2cm) -- (-1cm +1/6cm, 2cm) -- (-1cm + 1/8cm, -2cm) -- cycle; % , ,
shadowDepth0 := 4/3cm; % - «» ,
shadowPath1 := shadowPath0 rotated -60;
shadowDepth1 := 4/3cm;
draw sphere.c(2.4cm); % sphere.c tube.l
fill shadowPath0 withcolor white;
draw shadowPath0;
fill shadowPath1 withcolor white;
draw shadowPath1;
endfig;
Und natürlich brauchen Sie eine Holzstruktur. Der Einfluss der Art des Knotenwachstums auf das Muster von Abschnitten von Baumringen ist ein Thema für ernsthafte Forschung. Sehr vereinfacht können wir uns Jahresringe in parallelen Ebenen vorstellen, in die Verzerrungen der Knoten einführen. Es reicht also aus, die Änderung in der Ebene durch eine nicht sehr ausgefeilte Funktion (die Knotenfunktion) zu beschreiben und eine Reihe von Isolinien für die Summe der Menge solcher Funktionen als das gewünschte Muster von Baumringen zu betrachten.
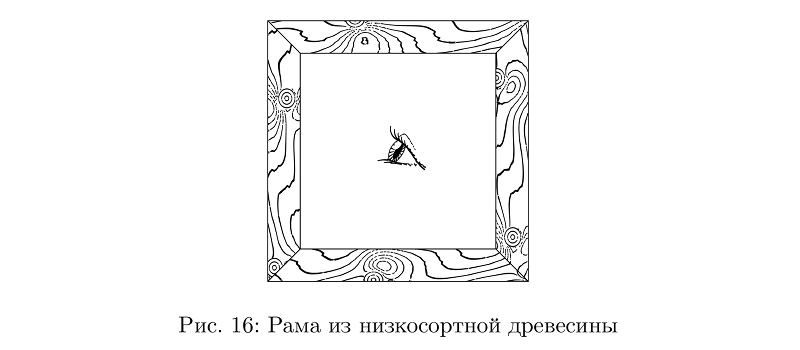
Beispielcodebeginfig(16);
numeric w, b;
pair A, B, C, D, A', B', C', D';
w := 4cm;
b := 1/2cm;
A := (0, 0);
A' := (b, b);
B := (0, w);
B' := (b, wb);
C := (w, w);
C' := (wb, wb);
D := (w, 0);
D' := (wb, b);
draw woodenThing(A--A'--B'--B--cycle, 0); % , A--A'--B'--B--cycle, 0
draw woodenThing(B--B'--C'--C--cycle, 90);
draw woodenThing(C--C'--D'--D--cycle, 0);
draw woodenThing(A--A'--D'--D--cycle, 90);
eyescale := 2/3cm; %
draw eye(150) shifted 1/2[A,C]; % 150
endfig;
Das Auge aus dem obigen Bild kann sich leicht öffnen, dann blinzeln und die Breite der Pupille ändert sich. Dies hat keine besondere Bedeutung, aber es wird lebhafter, als wenn solche Kleinigkeiten mechanisch überall gleich wären.

Beispielcodebeginfig(17);
eyescale := 2/3cm; % 1/2cm
draw eye(0) shifted (0cm, 0);
draw eye(0) shifted (1cm, 0);
draw eye(0) shifted (2cm, 0);
draw eye(0) shifted (3cm, 0);
draw eye(0) shifted (4cm, 0);
endfig;
Meistens waren die Bilder nicht sehr kompliziert, aber wenn Sie die Angelegenheit mit aller Ernsthaftigkeit angehen, müssen viele Aufgaben gelöst werden, um sie sinnvoll zu veranschaulichen. Nehmen wir zum Beispiel Lopitals Aufgabe bezüglich des Blocks an (ich weiß nicht, wie es auf Russisch richtig heißt, es war nicht im Lehrbuch, es ist nur ein Beispiel): Der Block hängt an einem Seil der Länge l, das an Punkt A aufgehängt ist, er ist an einem anderen Seil eingehakt Auf Punkt B in gleicher Höhe aufgehängt, hängt die Ladung C am zweiten Seil. Die Frage ist, wo sich die Ladung befindet, wenn die Seile und der Block schwerelos sind. Überraschenderweise sind sowohl die Lösung des Problems als auch die Konstruktion nicht so elementar, aber wenn Sie mit mehreren Variablen spielen, können Sie auf einfache Weise genau das Bild erstellen, das auf dem Streifen am besten aussieht, während es wahr bleibt.
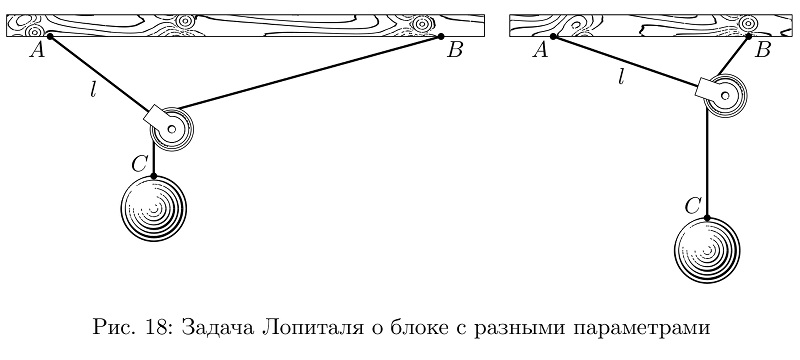
Beispielcodevardef lHopitalPulley (expr AB, l, m) = % AB l, m . ? : , , arithmetic overflow.
save A, B, C, D, E, o, a, x, y, d, w, h, support;
image(
pair A, B, C, D, E, o[];
path support;
numeric a, x[], y[], d[], w, h;
x1 := (l**2 + abs(l)*((sqrt(8)*AB)++l))/4AB; % ,
y1 := l+-+x1; %
y2 := m - ((AB-x1)++y1); %
A := (0, 0);
B := (AB*cm, 0);
D := (x1*cm, -y1*cm);
C := D shifted (0, -y2*cm);
d1 := 2/3cm; d2 := 1cm; d3 := 5/6d1; % ,
w := 2/3cm; h := 1/3cm; % . ,
o1 := (unitvector(CD) rotated 90 scaled 1/2d3);
o2 := (unitvector(DB) rotated 90 scaled 1/2d3);
E := whatever [D shifted o1, C shifted o1]
= whatever [D shifted o2, B shifted o2]; % ,
a := angle(AD);
support := A shifted (-w, 0) -- B shifted (w, 0) -- B shifted (w, h) -- A shifted (-w, h) -- cycle;
draw woodenThing(support, 0); % ,
draw pulley (d1, a - 90) shifted E; %
draw image(
draw A -- D -- B withpen thickpen;
draw D -- C withpen thickpen;
) maskedWith (pulleyOutline shifted E); %
draw sphere.c(d2) shifted C shifted (0, -1/2d2); %
dotlabel.llft(btex $A$ etex, A);
dotlabel.lrt(btex $B$ etex, B);
dotlabel.ulft(btex $C$ etex, C);
label.llft(btex $l$ etex, 1/2[A, D]);
)
enddef;
beginfig(18);
draw lHopitalPulley (6, 2, 11/2); % ,
draw lHopitalPulley (3, 5/2, 3) shifted (8cm, 0);
endfig;
Was ist ein Lehrbuch? Leider und ah, als fast alle Illustrationen und Layouts fertig waren, passierte dort etwas und er kam nie heraus. Daher habe ich wahrscheinlich einige Zeit später alle wichtigen Dinge aus der resultierenden Bibliothek erneut geschrieben und
den Code auf dem Github veröffentlicht . Einige Kunshtyuki sind dort nicht eingetreten: zum Beispiel Stromkreise oder eine Funktion zum Zeichnen von Autos und Traktoren. Einige - hinzugefügt: Knoten zum Beispiel.
Diese ganze Küche funktioniert nicht schnell: Es dauert ungefähr eine Minute, um alle Bilder für diesen Artikel mit LuaLaTeX auf meinem Laptop mit dem i5-4200U 1,6 GHz zu sammeln. Für so viele Dinge wird ein Pseudozufallszahlengenerator verwendet, sodass ähnliche Bilder nicht nur innerhalb eines Laufs (dies ist eine Funktion) etwas anders aussehen, sondern jeder nachfolgende Lauf Bilder ergibt, die sich von den vorherigen unterscheiden. Sie können jedoch immer
randomseed := - in der Präambel setzen, und alle gleichen Läufe erzeugen dieselben Bilder.