Übersetzung eines einfachen neuronalen NetzesWas werden wir tun? Wir werden versuchen, ein einfaches und sehr kleines neuronales Netzwerk zu erstellen, das wir Ihnen
erklären und
beibringen werden , etwas zu unterscheiden. Gleichzeitig werden wir nicht in die Geschichte und den mathematischen Dschungel gehen (solche Informationen sind sehr leicht zu finden) - stattdessen werden wir versuchen, Ihnen und uns selbst das Problem (nicht die Tatsache, dass es möglich sein wird) mit Zeichnungen und Code zu erklären.
Viele der Begriffe in neuronalen Netzen beziehen sich auf die Biologie. Beginnen wir also von vorne:
Das Gehirn ist eine komplizierte Sache, kann aber auch in mehrere Hauptteile und Operationen unterteilt werden:
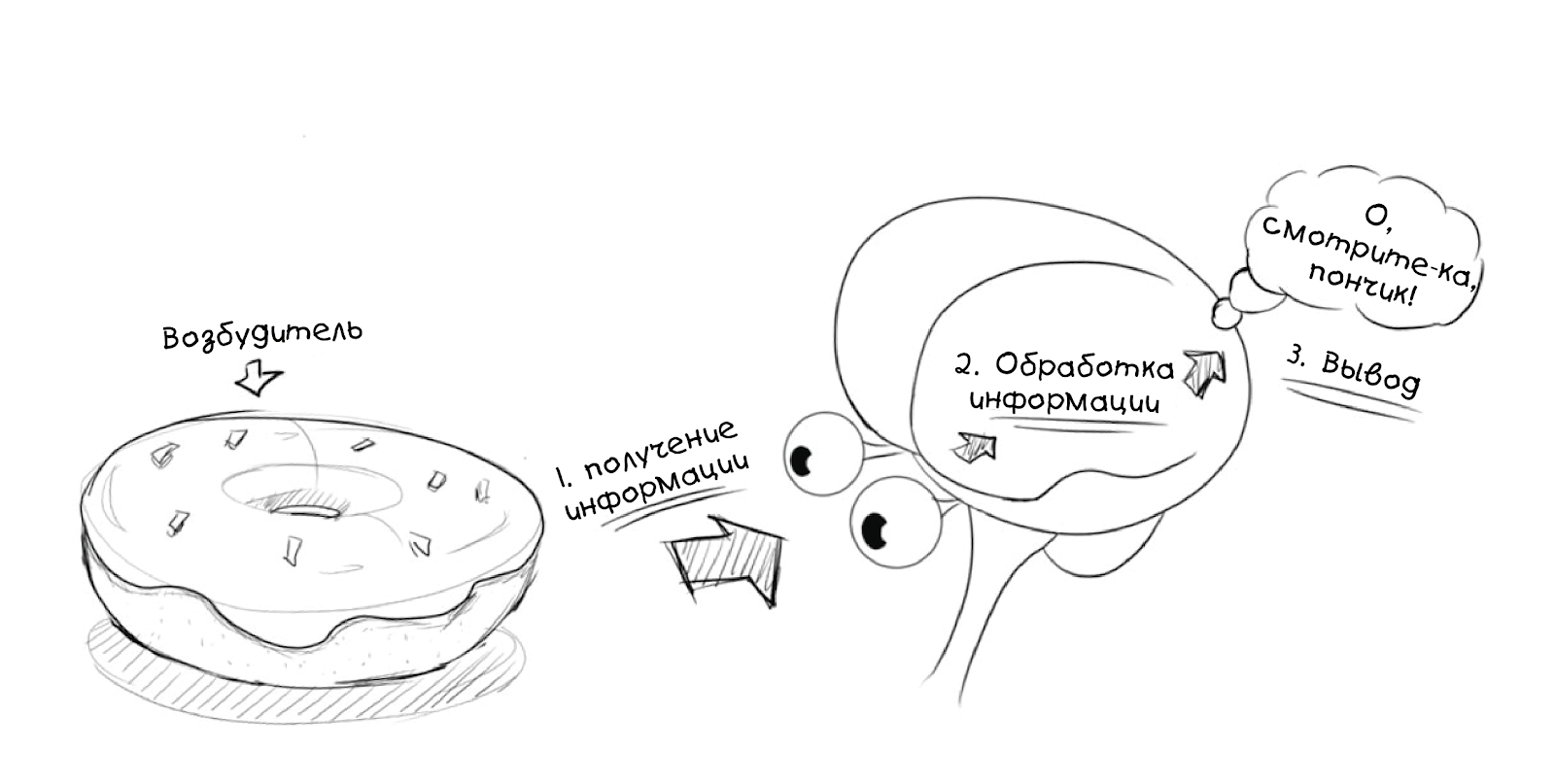
Der Erreger kann auch
intern sein (z. B. ein Bild oder eine Idee):
Schauen wir uns nun die grundlegenden und vereinfachten
Teile des Gehirns an:
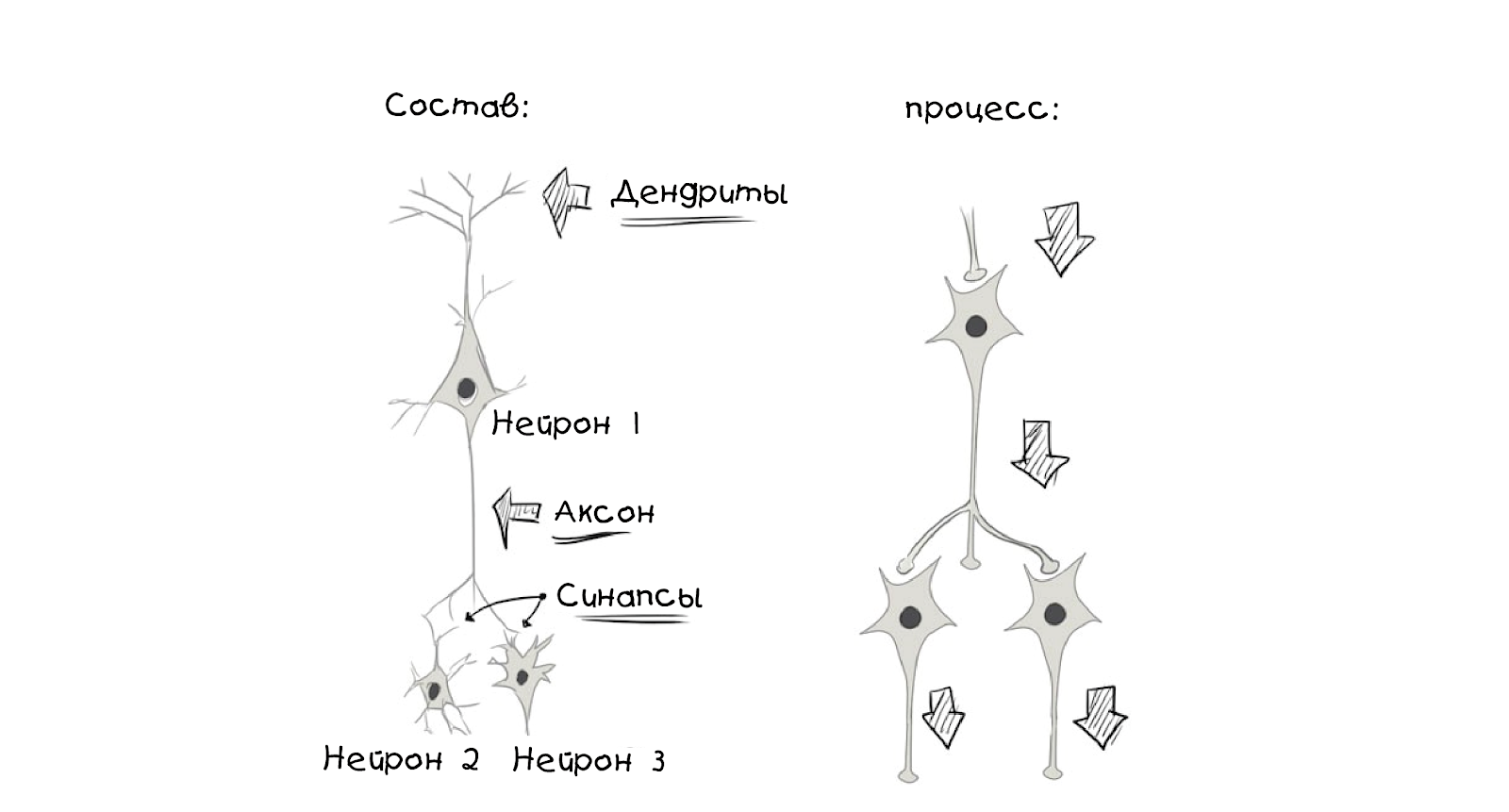
Das Gehirn sieht im Allgemeinen wie ein Kabelnetz aus.Ein Neuron ist die Haupteinheit des Kalküls im Gehirn, es empfängt und verarbeitet die chemischen Signale anderer Neuronen und erzeugt abhängig von einer Reihe von Faktoren entweder nichts oder erzeugt einen elektrischen Impuls oder ein Aktionspotential, das dann über Synapsen Signale an benachbarte
verbundene Neuronen sendet:
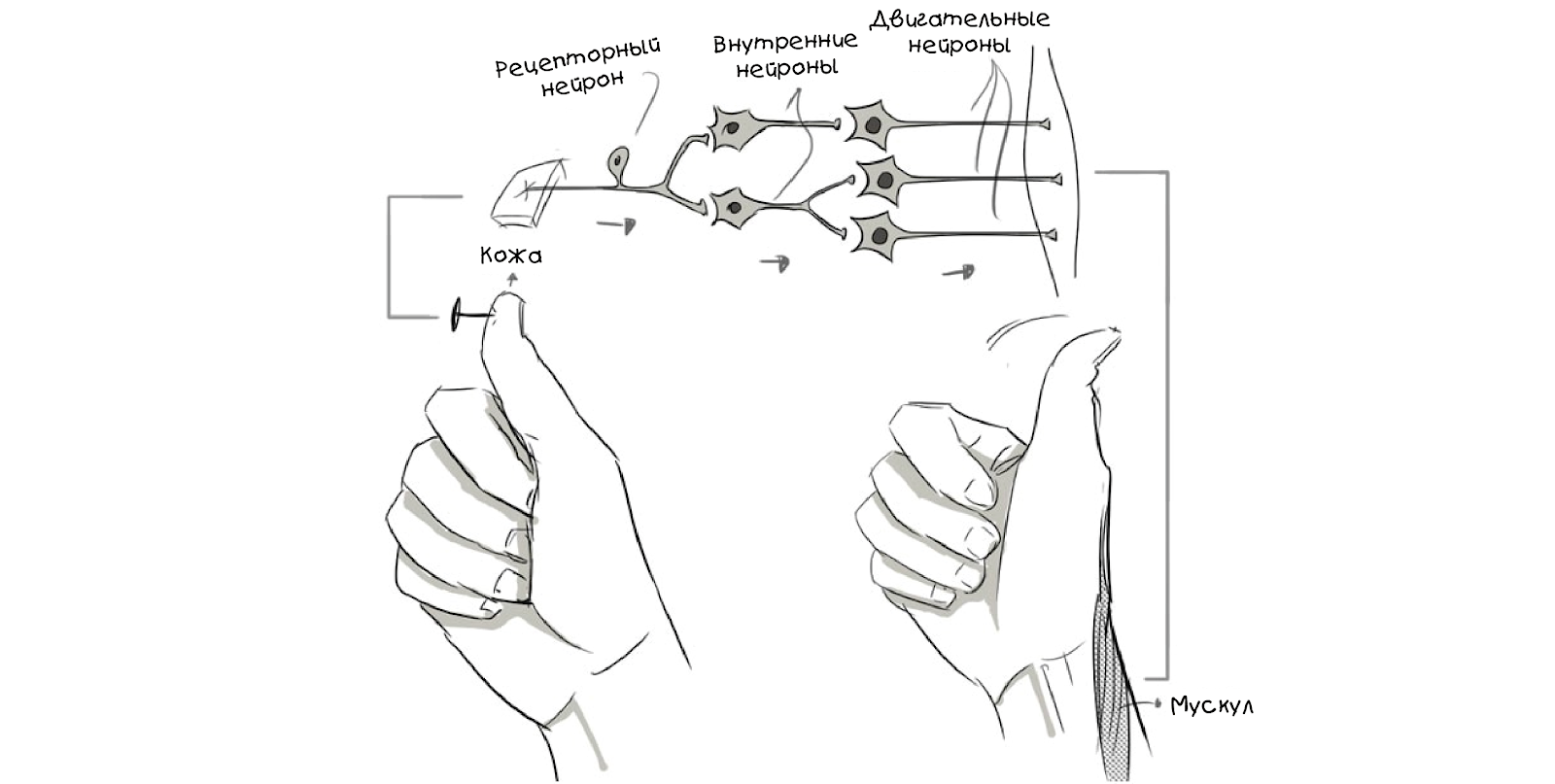
Träume, Erinnerungen, selbstregulierende Bewegungen, Reflexe und alles, was Sie denken oder tun, sind auf diesen Prozess zurückzuführen: Millionen oder sogar Milliarden von Neuronen arbeiten auf verschiedenen Ebenen und stellen Verbindungen her, die verschiedene parallele Subsysteme bilden und ein biologisches neuronales
Netzwerk darstellen .
Natürlich sind dies alles Vereinfachungen und Verallgemeinerungen, aber dank ihnen können wir eine einfache beschreiben
neuronales Netzwerk:
Und beschreiben Sie es formal anhand des Diagramms:
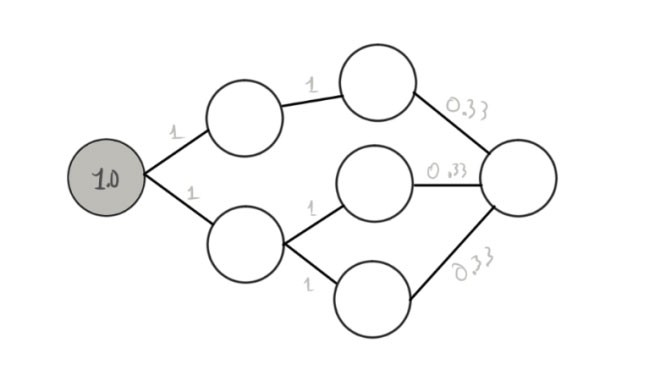
Hier ist eine Klarstellung erforderlich. Kreise sind Neuronen und Linien sind Verbindungen zwischen ihnen,
und um dies in diesem Stadium nicht zu komplizieren, ist die
Beziehung eine direkte Bewegung von Informationen
von links nach rechts . Das erste Neuron ist derzeit aktiv und ausgegraut. Wir haben ihm auch eine Nummer zugewiesen (1 - wenn es funktioniert, 0 - wenn nicht). Die Zahlen zwischen Neuronen geben das
Gewicht der Verbindung an.
Die obigen Grafiken zeigen den Zeitpunkt des Netzwerks. Für eine genauere Anzeige müssen Sie ihn in Zeiträume unterteilen:
Um Ihr eigenes neuronales Netzwerk zu erstellen, müssen Sie verstehen, wie sich Gewichte auf Neuronen auswirken und wie Neuronen trainiert werden. Nehmen Sie als Beispiel ein Kaninchen (Testkaninchen) und setzen Sie es unter die Bedingungen eines klassischen Experiments.
Wenn ein sicherer Luftstrom auf sie gerichtet ist, blinken Kaninchen wie Menschen:
Dieses Verhaltensmodell kann grafisch dargestellt werden:
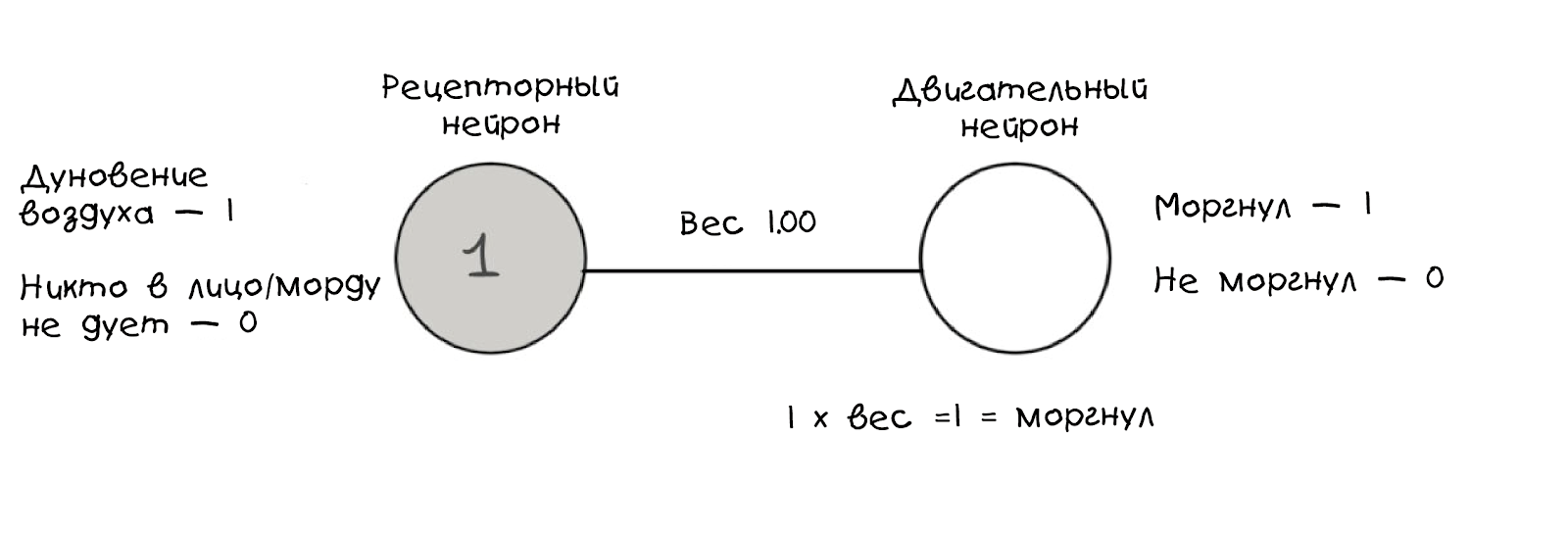
Wie im vorherigen Diagramm zeigen diese Grafiken nur den Moment, in dem das Kaninchen einen Atemzug spürt, und auf diese Weise
codieren wir
den Schlag als logischen Wert. Zusätzlich berechnen wir anhand des Gewichtswerts, ob das zweite Neuron ausgelöst wird. Wenn es 1 ist, dann wird das sensorische Neuron ausgelöst, wir blinken; Wenn das Gewicht weniger als 1 beträgt, blinken wir nicht: Das zweite Neuron hat eine
Grenze von 1.
Wir führen ein weiteres Element ein - ein sicheres Tonsignal:
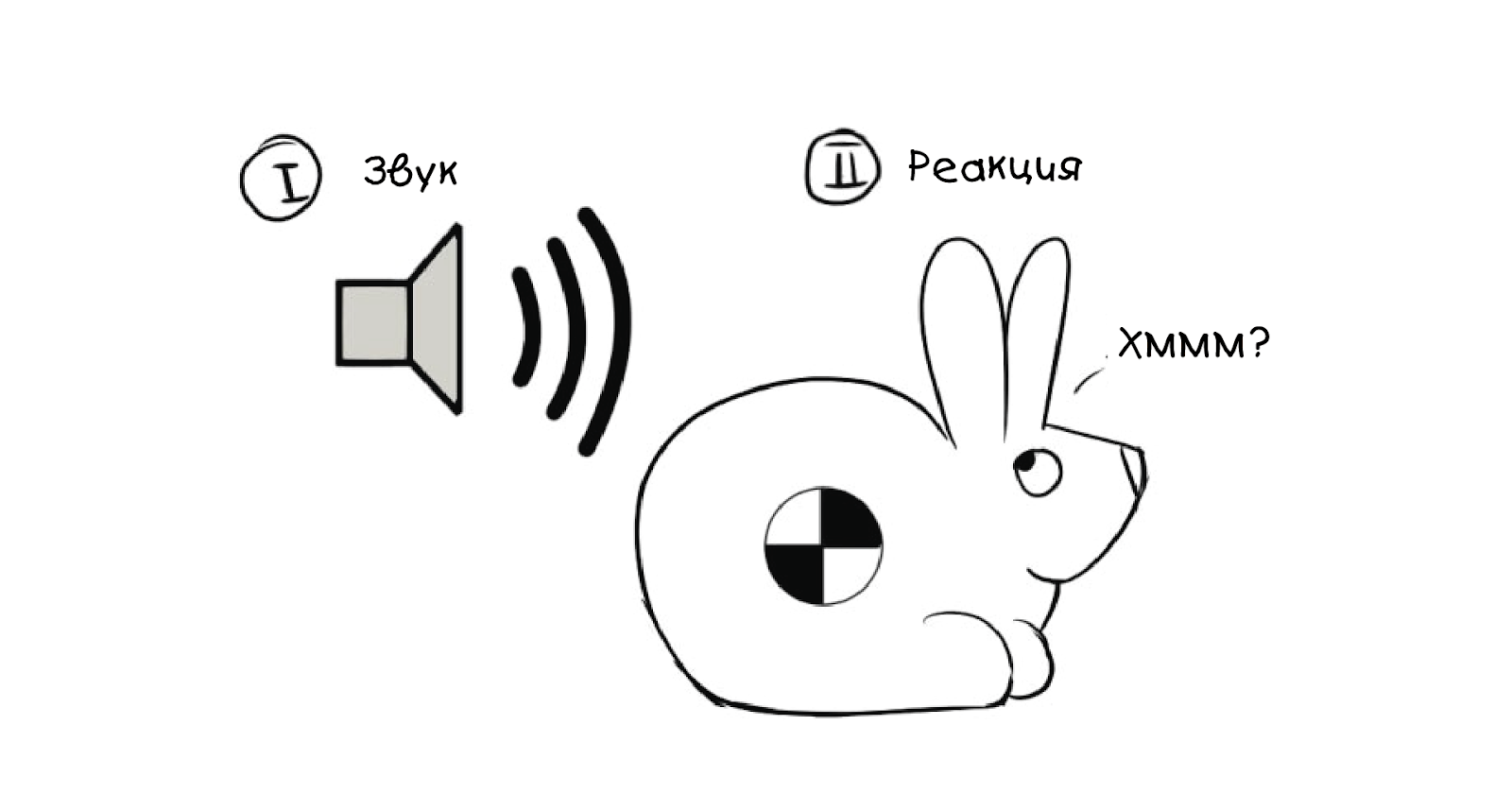
Wir können das Interesse eines Kaninchens wie folgt modellieren:
Der Hauptunterschied besteht darin, dass das Gewicht jetzt
Null ist , so dass wir zumindest vorerst kein blinkendes Kaninchen erhalten haben. Bringen Sie nun dem Kaninchen bei, im Team zu blinken und zu mischen
Reizstoffe (Tonsignal und Atem):
Es ist wichtig, dass diese Ereignisse in unterschiedlichen
Zeiträumen auftreten . In Diagrammen sieht dies folgendermaßen aus:
Der Ton selbst macht nichts, aber der Luftstrom lässt das Kaninchen immer noch blinken, und wir zeigen dies durch Gewichte multipliziert mit den Reizen (rot).
Das Erlernen komplexer Verhaltensweisen kann vereinfacht als allmähliche Gewichtsänderung zwischen verbundenen Neuronen im Laufe der Zeit ausgedrückt werden.
Wiederholen Sie die Schritte, um das Kaninchen zu trainieren:
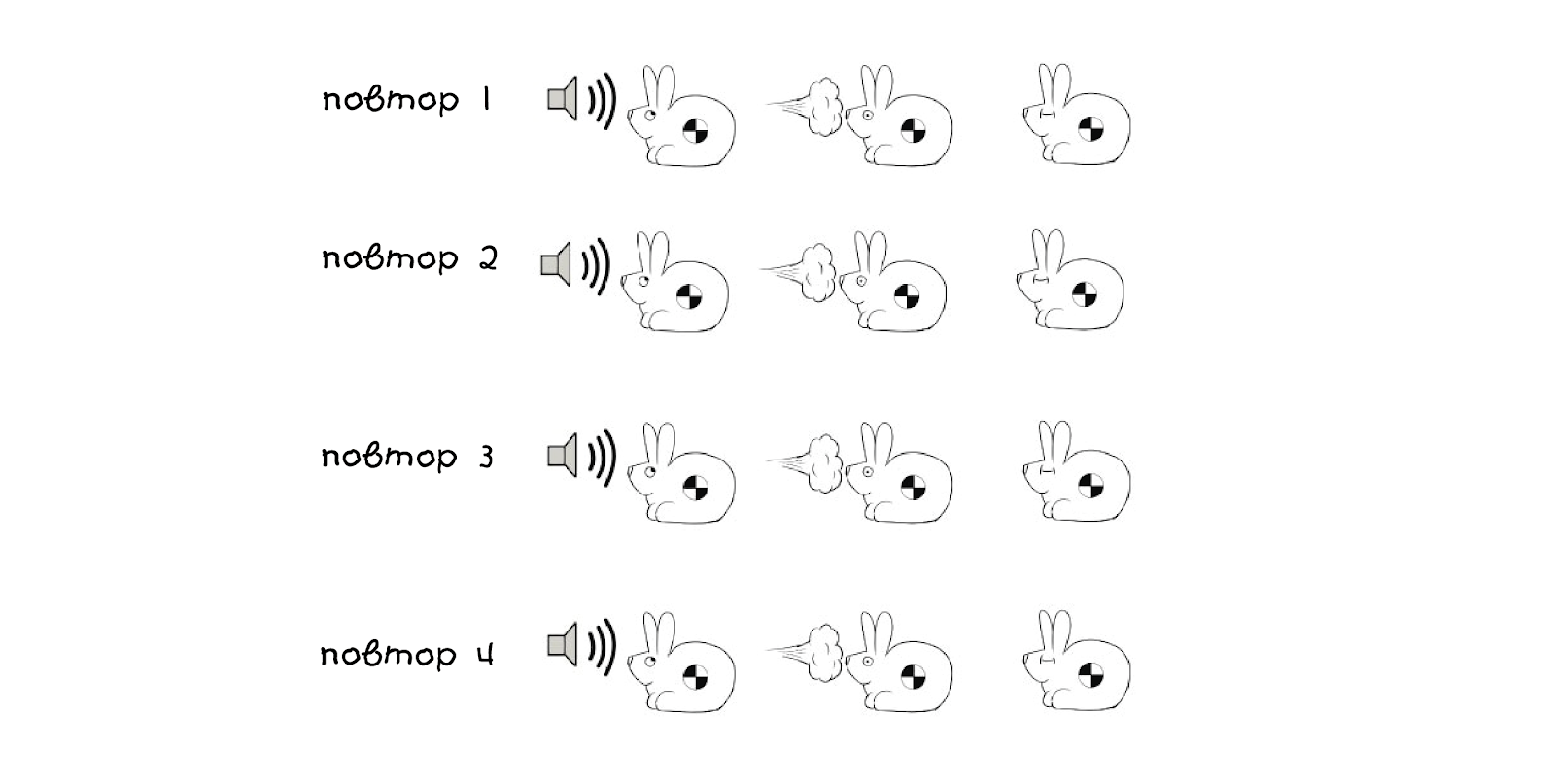
Bei den ersten drei Versuchen sehen die Schemata folgendermaßen aus:
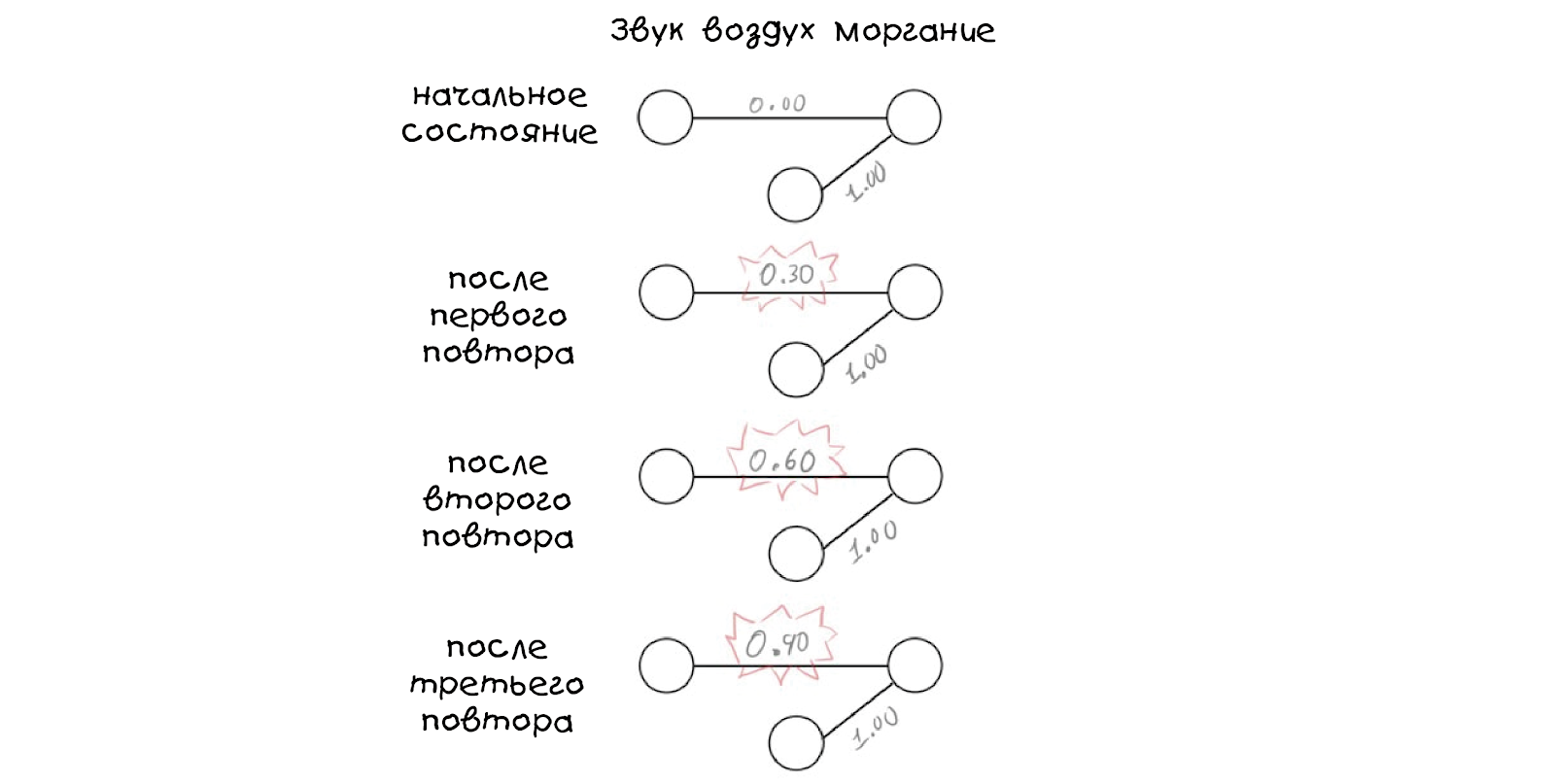
Beachten Sie, dass das Gewicht für den Schallreiz nach jeder Wiederholung zunimmt (rot hervorgehoben). Dieser Wert ist jetzt beliebig - wir haben 0,30 gewählt, aber die Zahl kann beliebig sein, auch negativ. Nach der dritten Wiederholung werden Sie keine Änderung im Verhalten des Kaninchens bemerken, aber nach der vierten Wiederholung wird etwas Überraschendes passieren - das Verhalten wird sich ändern.
Wir haben den Effekt aus der Luft entfernt, aber der Hase blinkt immer noch, als er einen Piepton hörte! Dieses letzte Verhalten kann dieses Verhalten erklären:
Wir haben das Kaninchen trainiert, auf Geräusche durch Blinken zu reagieren.
In einem realen Experiment dieser Art können mehr als 60 Wiederholungen erforderlich sein, um ein Ergebnis zu erzielen.Jetzt werden wir die biologische Welt des Gehirns und der Kaninchen verlassen und versuchen, alles daran anzupassen
lernte ein künstliches neuronales Netzwerk zu schaffen. Versuchen wir zunächst, eine einfache Aufgabe zu erledigen.
Nehmen wir an, wir haben eine Maschine mit vier Knöpfen, die Essen ausgibt, wenn Sie rechts drücken
Tasten (gut, oder Energie, wenn Sie ein Roboter sind). Die Aufgabe besteht darin herauszufinden, welcher Knopf die Belohnung gibt:
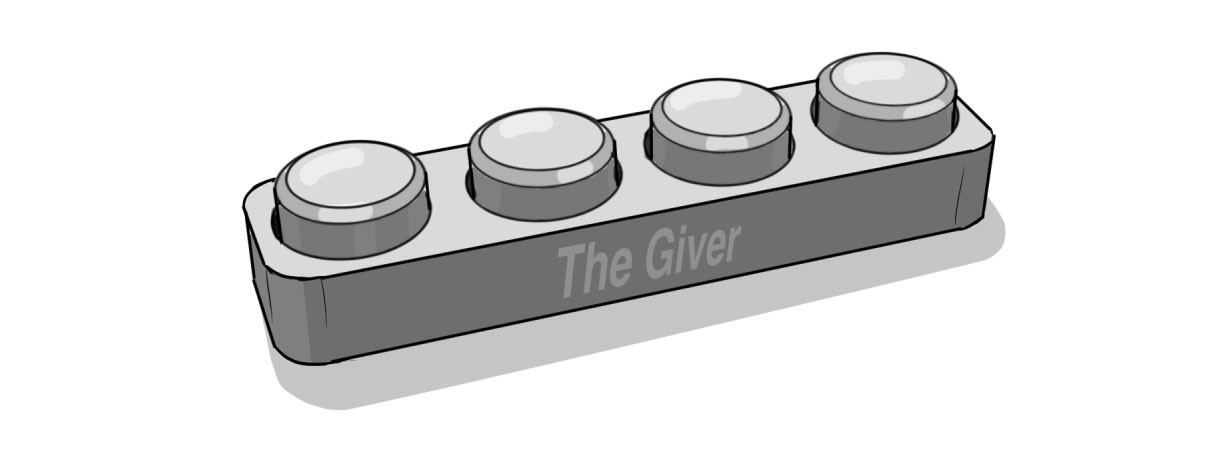
Wir können (schematisch) wie folgt darstellen, was die Schaltfläche beim Klicken bewirkt:
Dieses Problem lässt sich am besten in seiner Gesamtheit lösen. Schauen wir uns also alle möglichen Ergebnisse an, einschließlich der richtigen:
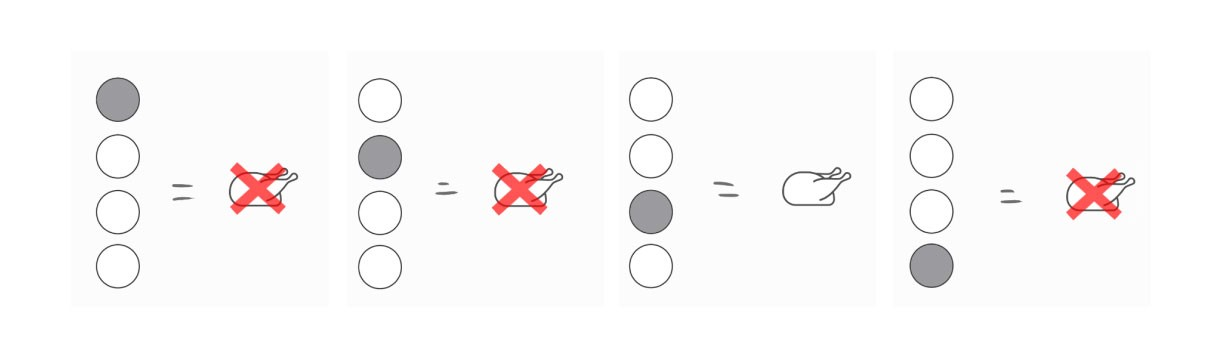Drücken Sie die 3. Taste, um Ihr Abendessen zu erhalten.Um ein neuronales Netzwerk im Code zu reproduzieren, müssen wir zuerst ein Modell oder einen Graphen erstellen, mit dem das Netzwerk verknüpft werden kann. Hier ist ein Diagramm, das für die Aufgabe geeignet ist. Außerdem zeigt es sein biologisches Gegenstück gut an:
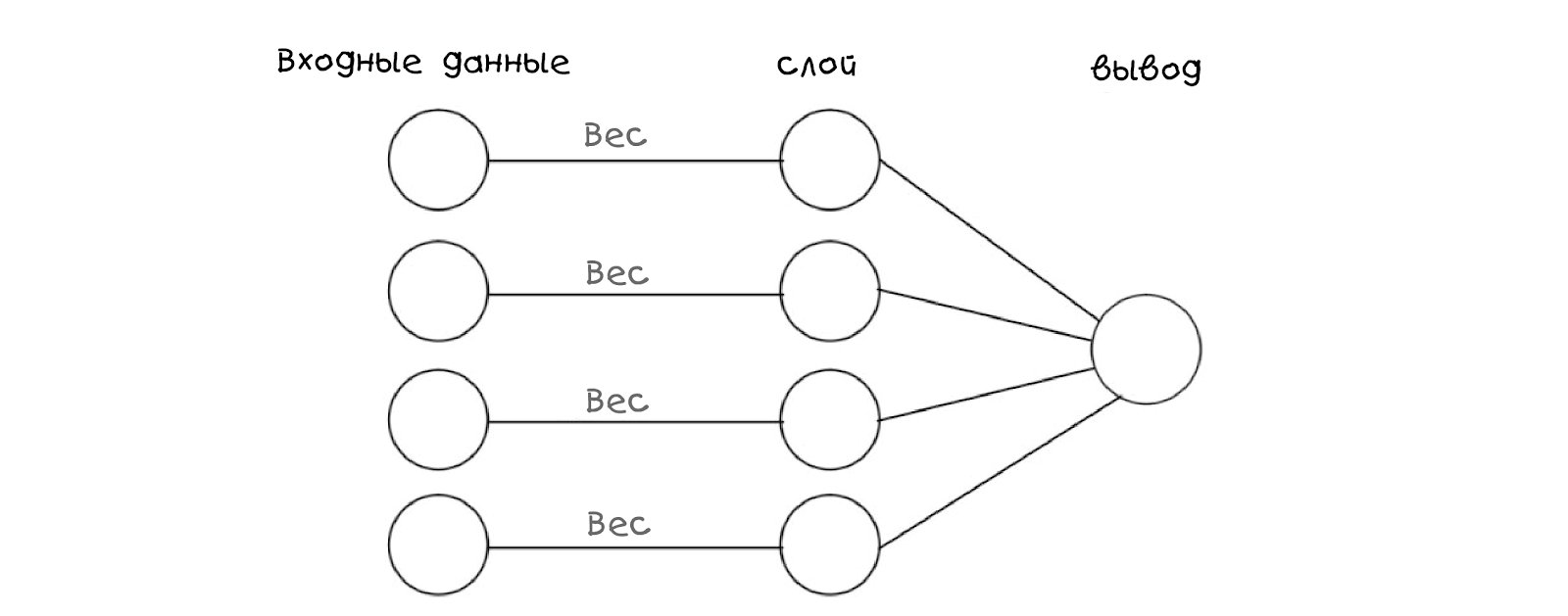
Dieses neuronale Netzwerk empfängt nur eingehende Informationen - in diesem Fall ist es die Wahrnehmung, welche Taste gedrückt wurde. Ferner ersetzt das Netzwerk die eingehenden Informationen durch Gewichte und zieht eine Schlussfolgerung basierend auf dem Hinzufügen einer Schicht. Es klingt etwas verwirrend, aber lassen Sie uns sehen, wie die Schaltfläche in unserem Modell dargestellt wird:
Beachten Sie, dass alle Gewichte 0 sind, sodass das neuronale Netzwerk wie ein Säugling vollständig leer, aber vollständig miteinander verbunden ist.Daher vergleichen wir das externe Ereignis mit der Eingangsschicht des neuronalen Netzwerks und berechnen den Wert an seiner Ausgabe. Es kann mit der Realität übereinstimmen oder auch nicht, aber im Moment werden wir es ignorieren und beginnen, die Aufgabe auf computerfreundliche Weise zu beschreiben. Beginnen wir mit der Eingabe von Gewichten (wir werden JavaScript verwenden):
var inputs = [0,1,0,0]; var weights = [0,0,0,0];
Der nächste Schritt besteht darin, eine Funktion zu erstellen, die Eingabewerte und Gewichte sammelt und den Wert am Ausgang berechnet:
function evaluateNeuralNetwork(inputVector, weightVector){ var result = 0; inputVector.forEach(function(inputValue, weightIndex) { layerValue = inputValue*weightVector[weightIndex]; result += layerValue; }); return (result.toFixed(2)); }
Wenn wir diesen Code ausführen, erhalten wir erwartungsgemäß das gleiche Ergebnis wie in unserem Modell oder Diagramm ...
evaluateNeuralNetwork(inputs, weights);
Live-Beispiel:
Neuronales Netz 001 .
Der nächste Schritt zur Verbesserung unseres neuronalen Netzwerks besteht darin, die eigenen Ausgabe- oder Ergebniswerte zu überprüfen, die mit der tatsächlichen Situation vergleichbar sind.
Lassen Sie uns zuerst diese besondere Realität in eine Variable kodieren:
Um Inkonsistenzen (und wie viele) zu erkennen, fügen wir eine Fehlerfunktion hinzu:
Error = Reality - Neural Net Output
Damit können wir die Leistung unseres neuronalen Netzwerks bewerten:
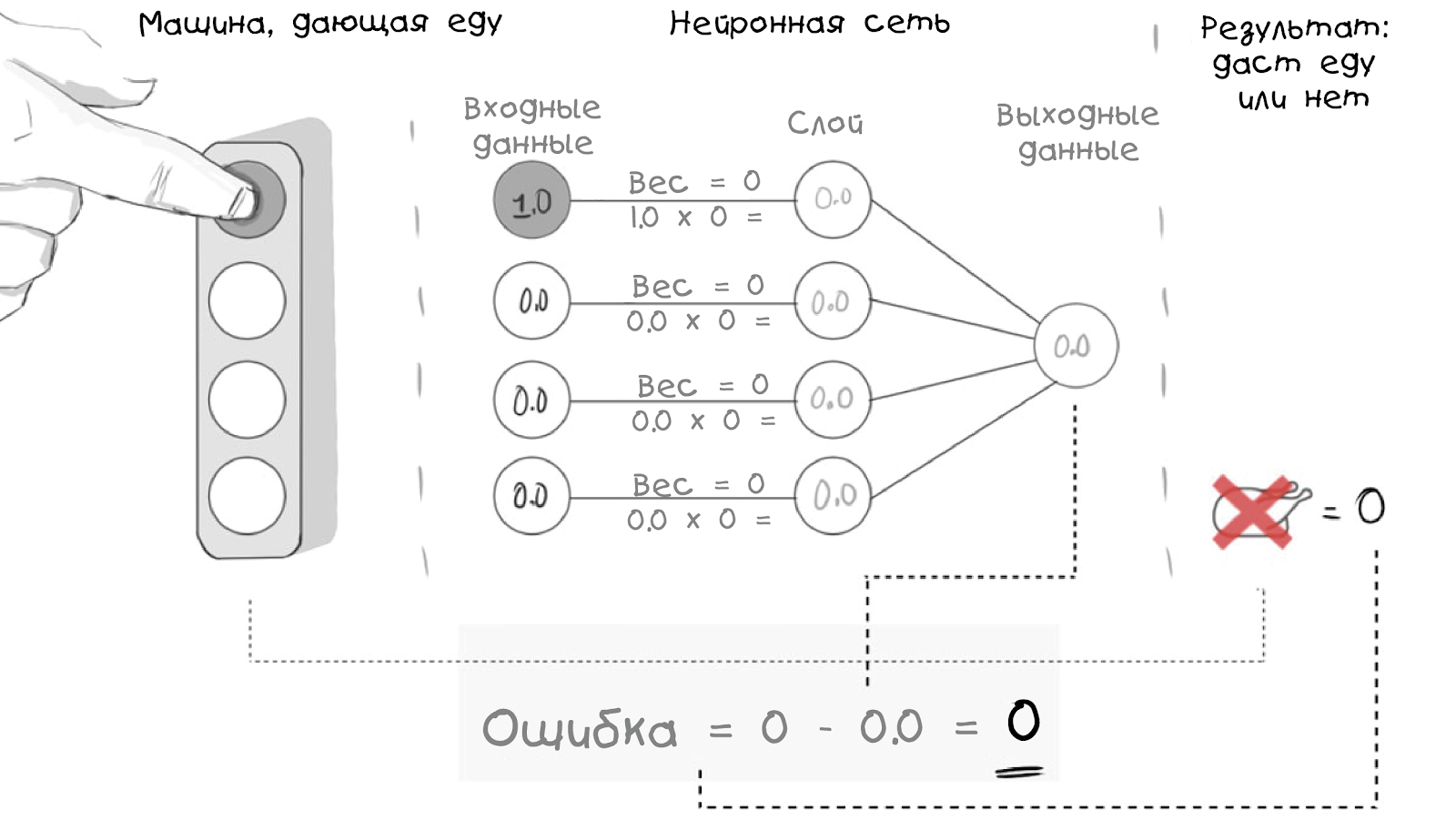
Aber was ist noch wichtiger mit Situationen, in denen die Realität ein positives Ergebnis liefert?
Jetzt wissen wir, dass unser neuronales Netzwerkmodell nicht funktioniert (und wir wissen, wie viel), großartig! Das ist großartig, weil wir jetzt die Fehlerfunktion verwenden können, um unser Lernen zu steuern. All dies ist jedoch sinnvoll, wenn wir die Fehlerfunktion wie folgt neu definieren:
Error = <b>Desired Output</b> - Neural Net Output
Eine schwer fassbare, aber so wichtige Diskrepanz, die stillschweigend zeigt, dass wir es tun werden
Verwenden Sie zuvor erhaltene Ergebnisse, um sie mit zukünftigen Aktionen zu vergleichen
(und für das Training, wie wir später sehen werden). Es existiert im wirklichen Leben, voll von
Muster wiederholen, so dass es eine evolutionäre Strategie werden kann (na ja, in
die meisten Fälle).
Als nächstes fügen wir in unserem Beispielcode eine neue Variable hinzu:
var input = [0,0,1,0]; var weights = [0,0,0,0]; var desiredResult = 1;
Und eine neue Funktion:
function evaluateNeuralNetError(desired,actual) { return (desired — actual); }
Live-Beispiel:
Neuronales Netz 002 .
Um die Zwischensumme zusammenzufassen . Wir haben mit der Aufgabe begonnen, ihr einfaches Modell in Form eines biologischen neuronalen Netzwerks erstellt und eine Möglichkeit gefunden, seine Leistung im Vergleich zur Realität oder zum gewünschten Ergebnis zu messen. Jetzt müssen wir einen Weg finden, um die Diskrepanz zu korrigieren - ein Prozess, der als Schulung für Computer und Menschen angesehen werden kann.
Wie trainiere ich ein neuronales Netzwerk?Die Grundlage für das Unterrichten sowohl biologischer als auch künstlicher neuronaler Netze ist die Wiederholung
und
Trainingsalgorithmen , daher werden wir separat mit ihnen arbeiten. Beginnen Sie mit
Lernalgorithmen.
In der Natur werden Lernalgorithmen als Änderungen der physikalischen oder chemischen Eigenschaften verstanden
Eigenschaften von Neuronen nach Experimenten:
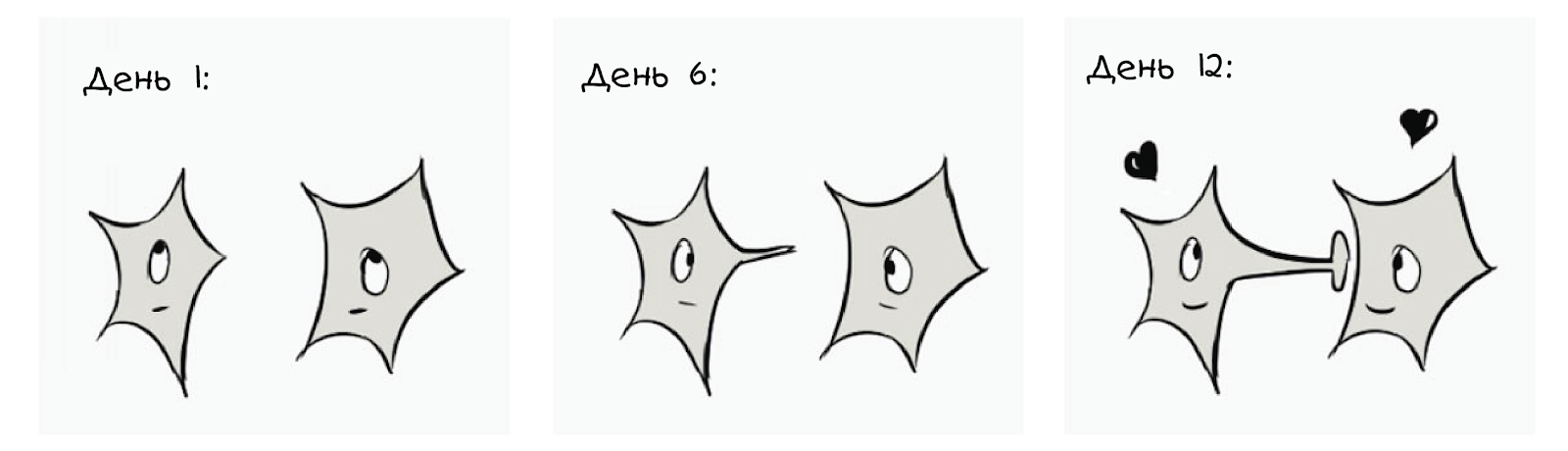
Ein dramatisches Beispiel dafür, wie sich zwei Neuronen im Code im Laufe der Zeit ändern, und unser Modell „Lernalgorithmus“ bedeuten, dass wir im Laufe der Zeit nur etwas ändern, um unser Leben einfacher zu machen. Fügen wir daher eine Variable hinzu, um den Grad der Erleichterung des Lebens anzugeben:
var learningRate = 0.20;
Und was wird sich ändern?Dies ändert das Gewicht (genau wie bei einem Kaninchen!), Insbesondere das Gewicht der Ausgabe, die wir wollen:
Wie Sie einen solchen Algorithmus codieren, ist Ihre Wahl. Der Einfachheit halber addiere ich den Trainingskoeffizienten zum Gewicht, hier in Form einer Funktion:
function learn(inputVector, weightVector) { weightVector.forEach(function(weight, index, weights) { if (inputVector[index] > 0) { weights[index] = weight + learningRate; } }); }
Bei Verwendung dieser Lernfunktion wird einfach unser Lernkoeffizient zum Gewichtsvektor des
aktiven Neurons addiert. Vor und nach dem Trainingskreis (oder der Wiederholung) sind die Ergebnisse wie folgt:
Live-Beispiel:
Neuronales Netz 003 .
Okay, jetzt, da wir uns in die richtige Richtung bewegen, wird das letzte Detail dieses Puzzles die Einführung von
Wiederholungen sein .
Es ist nicht so schwierig, in der Natur machen wir immer wieder dasselbe und im Code geben wir nur die Anzahl der Wiederholungen an:
var trials = 6;
Und die Einführung der Funktion der Anzahl der Wiederholungen in unser neuronales Trainingsnetzwerk wird folgendermaßen aussehen:
function train(trials) { for (i = 0; i < trials; i++) { neuralNetResult = evaluateNeuralNetwork(input, weights); learn(input, weights); } }
Nun, unser Abschlussbericht:
Neural Net output: 0.00 Error: 1.00 Weight Vector: [0,0,0,0] Neural Net output: 0.20 Error: 0.80 Weight Vector: [0,0,0.2,0] Neural Net output: 0.40 Error: 0.60 Weight Vector: [0,0,0.4,0] Neural Net output: 0.60 Error: 0.40 Weight Vector: [0,0,0.6,0] Neural Net output: 0.80 Error: 0.20 Weight Vector: [0,0,0.8,0] Neural Net output: 1.00 Error: 0.00 Weight Vector: [0,0,1,0]
Live-Beispiel:
Neuronales Netz 004 .
Jetzt haben wir einen Gewichtsvektor, der nur ein Ergebnis liefert (Huhn zum Abendessen), wenn der Eingabevektor der Realität entspricht (Drücken der dritten Taste).
Was ist so cool, was wir gerade gemacht haben?In diesem speziellen Fall kann unser neuronales Netzwerk (nach dem Training) die Eingabedaten erkennen und sagen, was zum gewünschten Ergebnis führt (wir müssen noch bestimmte Situationen programmieren):
Darüber hinaus ist es ein skalierbares Modell, Spielzeug und Werkzeug für unser Training. Wir konnten etwas Neues über maschinelles Lernen, neuronale Netze und künstliche Intelligenz lernen.
Achtung für Benutzer:
- Ein Speichermechanismus für die untersuchten Skalen ist nicht vorgesehen, sodass dieses neuronale Netzwerk alles vergisst, was es weiß. Wenn Sie den Code aktualisieren oder neu starten, benötigen Sie mindestens sechs erfolgreiche Wiederholungsversuche, damit das Netzwerk vollständig geschult ist, wenn Sie der Meinung sind, dass eine Person oder ein Computer zufällig Tasten drückt ... Dies dauert einige Zeit.
- Biologische Netzwerke zum Lernen wichtiger Dinge haben eine Lerngeschwindigkeit von 1, sodass Sie nur eine erfolgreiche Wiederholung benötigen.
- Es gibt einen Lernalgorithmus, der biologischen Neuronen sehr ähnlich ist. Er hat einen eingängigen Namen: Widroff-Hoff-Regel oder Widroff-Hoff-Training .
- Schwellenwerte von Neuronen (1 in unserem Beispiel) und die Auswirkungen der Umschulung (bei einer großen Anzahl von Wiederholungen beträgt das Ergebnis mehr als 1) werden nicht berücksichtigt, sind jedoch von Natur aus sehr wichtig und für große und komplexe Blöcke von Verhaltensreaktionen verantwortlich. Wie negative Gewichte.
Hinweise und Referenzen zur weiteren Lektüre
Ich habe versucht, Mathematik und strenge Begriffe zu vermeiden, aber wenn Sie interessiert sind, haben wir ein
Perzeptron erstellt , das als Algorithmus für das überwachte Lernen (
Lehren mit einem Lehrer ) von
Doppelklassifikatoren definiert ist - eine schwierige Sache.
Die biologische Struktur des Gehirns ist kein einfaches Thema, teils wegen Ungenauigkeit, teils wegen seiner Komplexität. Beginnen Sie am besten mit Neurowissenschaften (Purves) und kognitiven Neurowissenschaften (Gazzaniga). Ich habe das Kaninchenbeispiel von Gateway to Memory (Gluck) modifiziert und angepasst, das auch eine großartige Anleitung für die Graphwelt ist.
Eine weitere großartige Ressource, Eine Einführung in neuronale Netze (Gurney), ist für alle Ihre AI-bezogenen Anforderungen geeignet.
Und jetzt in Python! Vielen Dank an Ilya Andschmidt für die bereitgestellte Python-Version:
inputs = [0, 1, 0, 0] weights = [0, 0, 0, 0] desired_result = 1 learning_rate = 0.2 trials = 6 def evaluate_neural_network(input_array, weight_array): result = 0 for i in range(len(input_array)): layer_value = input_array[i] * weight_array[i] result += layer_value print("evaluate_neural_network: " + str(result)) print("weights: " + str(weights)) return result def evaluate_error(desired, actual): error = desired - actual print("evaluate_error: " + str(error)) return error def learn(input_array, weight_array): print("learning...") for i in range(len(input_array)): if input_array[i] > 0: weight_array[i] += learning_rate def train(trials): for i in range(trials): neural_net_result = evaluate_neural_network(inputs, weights) learn(inputs, weights) train(trials)
Und jetzt auf GO! Vielen Dank für diese Version von Kieran Maher.
package main import ( "fmt" "math" ) func main() { fmt.Println("Creating inputs and weights ...") inputs := []float64{0.00, 0.00, 1.00, 0.00} weights := []float64{0.00, 0.00, 0.00, 0.00} desired := 1.00 learningRate := 0.20 trials := 6 train(trials, inputs, weights, desired, learningRate) } func train(trials int, inputs []float64, weights []float64, desired float64, learningRate float64) { for i := 1; i < trials; i++ { weights = learn(inputs, weights, learningRate) output := evaluate(inputs, weights) errorResult := evaluateError(desired, output) fmt.Print("Output: ") fmt.Print(math.Round(output*100) / 100) fmt.Print("\nError: ") fmt.Print(math.Round(errorResult*100) / 100) fmt.Print("\n\n") } } func learn(inputVector []float64, weightVector []float64, learningRate float64) []float64 { for index, inputValue := range inputVector { if inputValue > 0.00 { weightVector[index] = weightVector[index] + learningRate } } return weightVector } func evaluate(inputVector []float64, weightVector []float64) float64 { result := 0.00 for index, inputValue := range inputVector { layerValue := inputValue * weightVector[index] result = result + layerValue } return result } func evaluateError(desired float64, actual float64) float64 { return desired - actual }