In der Tat ist er der meiste. Aber das Wichtigste zuerst.
Erklärung des Problems
Ich beherrsche Python, löse alles auf Codewars. Ich stoße auf eine bekannte Aufgabe über einen Wolkenkratzer und Eier. Der einzige Unterschied besteht darin, dass die Quelldaten nicht 100 Stockwerke und 2 Eier sind, sondern etwas mehr.
Gegeben: N Eier, M versucht sie zu werfen, endloser Wolkenkratzer.
Definieren: Der maximale Boden, von dem aus Sie ein Ei werfen können, ohne zu brechen. Eier sind im Vakuum kugelförmig und wenn eines von ihnen nicht bricht und beispielsweise aus dem 99. Stock fällt, halten die anderen auch einem Sturz aus allen Stockwerken unter einem Hundertstel stand.
0 <= N, M <= 20.000.
Die Laufzeit von zwei Dutzend Tests beträgt 12 Sekunden.
Suche nach einer Lösung
Wir müssen eine Funktionshöhe (n, m) schreiben, die die Bodennummer für das angegebene n, m zurückgibt. Da es sehr oft erwähnt wird und jedes Mal, wenn Sie "Höhe" Faulheit schreiben, werde ich es überall außer dem Code als f (n, m) bezeichnen.
Beginnen wir mit Nullen. Wenn es keine Eier gibt oder versucht wird, sie zu werfen, kann natürlich nichts bestimmt werden und die Antwort ist Null.
f (0, m) = 0, f (n, 0) = 0.Angenommen, es gibt ein Ei und es gibt 10 Versuche. Sie können alles riskieren und es sofort aus dem hundertsten Stock werfen, aber im Falle eines Fehlers können Sie nichts anderes bestimmen. Es ist also logischer, vom ersten Stock aus zu beginnen und nach jedem Wurf einen Stock nach oben zu gehen. bis entweder der Versuch oder das Ei endet. Das Maximum, wo Sie bekommen können, wenn das Ei nicht versagt, ist Boden Nummer 10.
f (1, m) = mNehmen Sie das zweite Ei, versuchen Sie es erneut 10. Nun, dann können Sie eine Chance mit einem Hundertstel eingehen? Wenn es kaputt geht, gibt es noch einen und 9 Versuche, mindestens 9 Stockwerke können passieren. Vielleicht müssen Sie also nicht vom hundertsten, sondern vom zehnten riskieren? Ist logisch. Bei Erfolg bleiben dann 2 Eier und 9 Versuche übrig. Analog dazu müssen Sie jetzt weitere 9 Stockwerke hinaufsteigen. Mit einer Reihe von Erfolgen - weitere 8, 7, 6, 5, 4, 3, 2 und 1. Insgesamt befinden wir uns mit zwei ganzen Eiern im 55. Stock und ohne es zu versuchen. Die Antwort ist die Summe der ersten M Mitglieder der arithmetischen Folge mit dem ersten Element 1 und Schritt 1.
f (2, m) = (m * m + m) / 2 . Es ist auch klar, dass bei jedem Schritt die Funktion f (1, m) aufgerufen wurde, aber dies ist noch nicht genau.
Fahren Sie mit drei Eiern und zehn Versuchen fort. Im Falle eines erfolglosen ersten Wurfs werden die mit 2 Eiern und 9 Versuchen bedeckten Böden von unten bedeckt, was bedeutet, dass der erste Wurf vom Boden f (2, 9) + 1 ausgeführt werden muss. Wenn dies erfolgreich ist, haben wir 3 Eier und 9 Versuche . Und für den zweiten Versuch müssen Sie weitere f (2.8) + 1 Stockwerke hinaufsteigen. Und so weiter, bis 3 Eier und 3 Versuche an den Händen bleiben. Und dann ist es Zeit, sich ablenken zu lassen, indem man Fälle mit N = M betrachtet, in denen es so viele Eier gibt, wie es Versuche gibt.
Und zur gleichen Zeit, wenn es mehr Eier gibt.Aber hier ist alles offensichtlich - Eier jenseits derjenigen, die brechen, werden für uns nicht nützlich sein, selbst wenn jeder Wurf erfolglos ist. f (n, m) = f (m, m), wenn n> m ist . Und alles in allem 3 Eier, 3 Würfe. Wenn das erste Ei zerbricht, können Sie f (2, 2) Stockwerke nach unten überprüfen, und wenn es nicht bricht, dann f (3,2) Stockwerke nach oben, dh das gleiche f (2, 2). Insgesamt f (3, 3) = 2 * f (2, 2) + 1 = 7. Und f (4, 4) besteht analog aus zwei f (3, 3) und einem, und es wird 15. Alle sein es ähnelt den Zweierpotenzen, und wir schreiben: f (m, m) = 2 ^ m - 1 .
Es sieht aus wie eine binäre Suche in der physischen Welt: Wir gehen von der Etage Nummer 2 ^ (m-1) aus, im Erfolgsfall gehen wir 2 ^ (m-2) Etagen höher und im Falle eines Misserfolgs gehen wir so viel runter und so weiter. bis die Versuche ausgehen. In unserem Fall stehen wir die ganze Zeit auf.
Kehren wir zu f (3, 10) zurück. Tatsächlich kommt es bei jedem Schritt auf die Summe f (2, m-1) an - die Anzahl der Stockwerke, die im Falle eines Ausfalls bestimmt werden können, Einheiten und f (3, m-1) - die Anzahl der Stockwerke, die im Erfolgsfall bestimmt werden können. Und es wird deutlich, dass es aufgrund der Zunahme der Anzahl der Eier und Versuche unwahrscheinlich ist, dass sich etwas ändert.
f (n, m) = f (n - 1, m - 1) + 1 + f (n, m - 1) . Und dies ist eine universelle Formel, die in Code implementiert werden kann.
from functools import lru_cache @lru_cache() def height(n,m): if n==0 or m==0: return 0 elif n==1: return m elif n==2: return (m**2+m)/2 elif n>=m: return 2**n-1 else: return height(n-1,m-1)+1+height(n,m-1)
Natürlich bin ich zuvor auf den Rechen der nicht-meroisierenden rekursiven Funktionen getreten und habe herausgefunden, dass f (10, 40) mit der Anzahl der Aufrufe an sich fast 40 Sekunden dauert - 97806983. Aber das Memoisieren wird auch nur in den Anfangsintervallen gespeichert. Wenn f (200.400) in 0,8 Sekunden ausgeführt wird, ist f (200, 500) bereits in 31 Sekunden. Es ist lustig, dass bei der Messung der Laufzeit mit% timeit das Ergebnis viel weniger als real ist. Offensichtlich dauert der erste Durchlauf der Funktion die meiste Zeit, während der Rest einfach die Ergebnisse seiner Memoisierung verwendet. Lügen, eklatante Lügen und Statistiken.
Rekursion ist nicht erforderlich, wir schauen weiter
So erscheint zum Beispiel in den Tests f (9477, 10000), aber mein erbärmliches f (200, 500) passt nicht mehr zum richtigen Zeitpunkt. Es gibt also eine andere Lösung, ohne Rekursion werden wir die Suche fortsetzen. Ich habe den Code ergänzt, indem ich Funktionsaufrufe mit bestimmten Parametern gezählt habe, um zu sehen, in was er sich letztendlich zerlegt hat. Für 10 Versuche wurden die folgenden Ergebnisse erhalten:
f (3,10) = 7+ 1 · f (2,9) + 1 · f (2,8) + 1 · f (2,7) + 1 · f (2,6) + 1 · f (2 , 5) + 1 · f (2,4) + 1 · f (2,3) + 1 · f (3,3)
f (4,10) = 27+ 1 · f (2,8) + 2 · f (2,7) + 3 · f (2,6) + 4 · f (2,5) + 5 · f (2 , 4) + 6 · f (2,3) + 6 · f (3,3) + 1 · f (4,4)
f (5,10) = 55+ 1 · f (2,7) + 3 · f (2,6) + 6 · f (2,5) + 10 · f (2,4) + 15 · f (2 , 3) + 15 · f (3,3) + 5 · f (4,4) + 1 · f (5,5)
f (6,10) = 69+ 1 · f (2,6) + 4 · f (2,5) + 10 · f (2,4) + 20 · f (2,3) + 20 · f (3 , 3) + 10 · f (4,4) + 4 · f (5,5) + 1 · f (6,6)
f (7,10) = 55+ 1 · f (2,5) + 5 · f (2,4) + 15 · f (2,3) + 15 · f (3,3) + 10 · f (4) , 4) + 6 · f (5,5) + 3 · f (6,6) + 1 · f (7,7)
f (8,10) = 27+ 1 · f (2,4) + 6 · f (2,3) + 6 · f (3,3) + 5 · f (4,4) + 4 · f (5) , 5) + 3 · f (6,6) + 2 · f (7,7) + 1 · f (8,8)
f (9,10) = 7+ 1 · f (2,3) + 1 · f (3,3) + 1 · f (4,4) + 1 · f (5,5) + 1 · f (6) , 6) + 1 · f (7,7) + 1 · f (8,8) + 1 · f (9,9)
Eine gewisse Regelmäßigkeit ist sichtbar:

Diese Koeffizienten werden theoretisch berechnet. Jedes Blau ist die Summe von oben und links. Und die violetten sind die gleichen blauen, nur in umgekehrter Reihenfolge. Sie können rechnen, aber dies ist wieder eine Rekursion, und darin war ich enttäuscht. Höchstwahrscheinlich haben viele (es ist schade, dass ich es nicht bin) diese Zahlen bereits gelernt, aber im Moment werde ich die Intrige nach meiner eigenen Lösung beibehalten. Ich beschloss, auf sie zu spucken und auf die andere Seite zu gehen.
Er öffnete das Exel, baute eine Platte mit den Ergebnissen der Funktion und begann nach Mustern zu suchen. C3 = IF (C $ 2> $ B3; 2 ^ $ B3-1; C2 + B2 + 1), wobei $ 2 die Zeile mit der Anzahl der Eier (1-13) ist, $ B die Spalte mit der Anzahl der Versuche (1-20) ist; C3 - Zelle am Schnittpunkt zweier Eier und eines Versuchs.
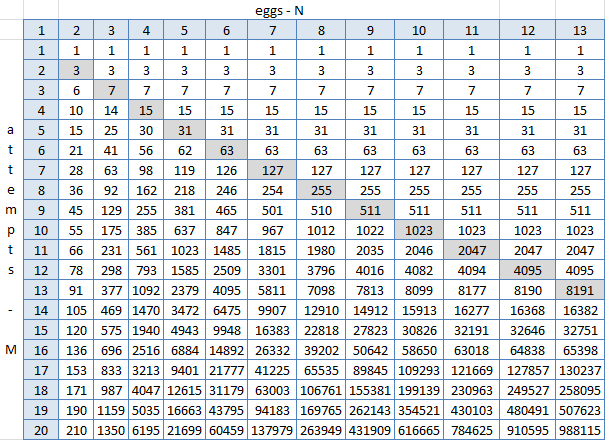
Die graue Diagonale ist N = M, und hier ist deutlich zu erkennen, dass sich rechts davon (für N> M) nichts ändert. Es kann gesehen werden - aber es kann nicht anders sein, denn dies sind alle Ergebnisse der Arbeit der Formel, in der angegeben wird, dass jede Zelle gleich der Summe von oben, oben links und eins ist. Es wurde jedoch keine universelle Formel gefunden, bei der Sie N und M ersetzen und die Bodennummer erhalten können. Spoiler: existiert nicht. Aber dann ist es so einfach, diese Tabelle in Excel zu erstellen. Vielleicht ist es möglich, dieselbe Python zu generieren und Antworten daraus zu ziehen.
Numpy tust du nicht
Ich erinnere mich, dass es NumPy gibt, das nur für die Arbeit mit mehrdimensionalen Arrays entwickelt wurde. Warum probieren Sie es nicht aus? Zunächst benötigen wir ein eindimensionales Array von Nullen der Größe N + 1 und ein eindimensionales Array von Einheiten der Größe N. Nehmen Sie das erste Array von Null zum vorletzten Element und fügen Sie es elementweise mit dem ersten Array vom ersten bis zum letzten Element und mit einem Array von Einheiten hinzu. Fügen Sie dem resultierenden Array am Anfang Null hinzu. M-mal wiederholen. Die Elementnummer N des resultierenden Arrays ist die Antwort. Die ersten 3 Schritte sehen folgendermaßen aus:
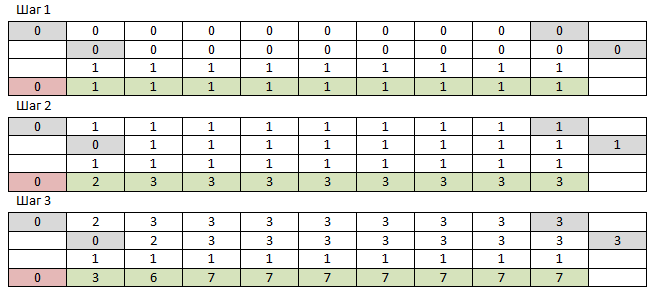
NumPy arbeitet so schnell, dass ich nicht die gesamte Tabelle gespeichert habe - jedes Mal, wenn ich die erforderliche Zeile erneut lese. Eine Sache - das Ergebnis der Arbeit an großen Zahlen war falsch. Höhere Ränge sind wie diese, die niedrigeren nicht. So sehen die arithmetischen Fehler von Gleitkommazahlen aus, die sich aus mehreren Additionen ergeben. Es spielt keine Rolle - Sie können den Typ des Arrays in int ändern. Nein, Ärger - es stellte sich heraus, dass NumPy aus Gründen der Geschwindigkeit nur mit seinen Datentypen arbeitet und sein int im Gegensatz zum Python int nicht mehr als 2 ^ 64-1 sein kann. Danach läuft es still über und fährt mit -2 ^ 64 fort. Und ich erwarte tatsächlich Zahlen unter dreitausend Zeichen. Aber es funktioniert sehr schnell, f (9477, 10000) läuft 233 ms, es stellt sich nur eine Art Unsinn am Ausgang heraus. Ich werde nicht einmal den Code geben, da so etwas. Ich werde versuchen, dasselbe zu einer sauberen Python zu machen.
Iteriert, iteriert, aber nicht iteriert
def height(n, m): arr = [0]*(n+1) while m > 0: arr = [0] + list(map(lambda x,y: x+y+1, arr[:-1], arr[1:])) m-=1 return arr[n]
44 Sekunden zur Berechnung von f (9477, 10000) sind etwas viel. Aber absolut sicher. Was kann optimiert werden? Erstens muss nicht alles rechts von der Diagonale M, M betrachtet werden. Die zweite - das letzte Array als Ganzes für eine Zelle zu betrachten. Dazu passen die letzten beiden Zellen der vorherigen. Um f (10, 20) zu berechnen, reichen nur diese grauen Zellen aus:
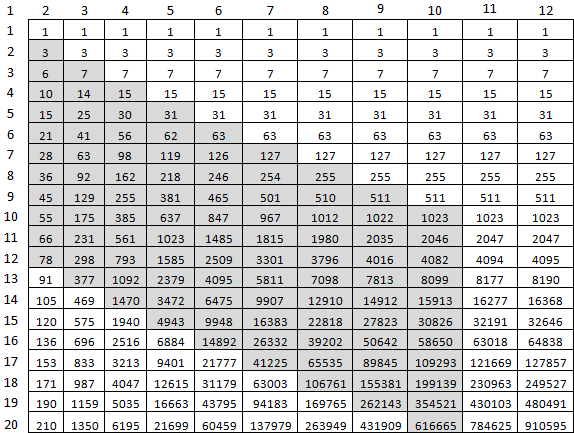
Und so sieht es im Code aus:
def height(n, m): arr = [0, 1, 1] i = 1 while i < n and i < mn:
Und was denkst du? f (9477, 10000) in 2 Sekunden! Diese Eingabe ist jedoch zu gut. Die Länge des Arrays beträgt zu jedem Zeitpunkt nicht mehr als 533 Elemente (10000-9477). Lassen Sie uns f (5477, 10000) - 11 Sekunden überprüfen. Es ist auch gut, aber nur im Vergleich zu 44 Sekunden - zwanzig Tests mit dieser Zeit werden nicht bestanden.
Das ist es nicht. Aber da es eine Aufgabe gibt, dann gibt es eine Lösung, die Suche wird fortgesetzt. Ich fing wieder an, die Excel-Tabelle zu betrachten. Die Zelle links von (m, m) ist immer eins weniger. Und die Zelle links davon ist nicht mehr da, in jeder Reihe wird der Unterschied größer. Die Zelle darunter (m, m) ist immer doppelt so groß. Und die Zelle darunter ist nicht mehr zweimal, sondern etwas kleiner, aber für jede Spalte anders, je weiter, desto größer. Und auch die Zahlen in einer Zeile wachsen zunächst schnell und nach der Mitte langsam. Lassen Sie mich eine Tabelle mit Unterschieden zwischen benachbarten Zellen erstellen. Vielleicht wird dort welches Muster angezeigt?
Wärmer
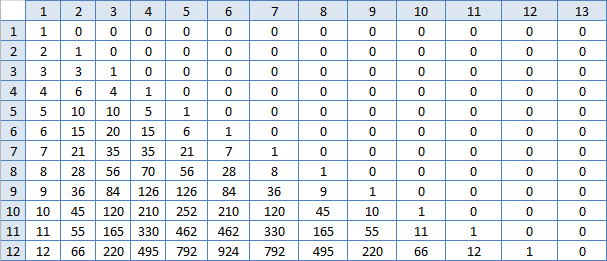
Bah, vertraute Zahlen! Das heißt, die Summe N dieser Zahlen in der Zeilennummer M ist dies die Antwort? Es stimmt, sie zu zählen ist ungefähr das gleiche wie das, was ich bereits getan habe. Es ist unwahrscheinlich, dass dies die Arbeit erheblich beschleunigen wird. Aber du musst versuchen:
f (9477, 10000): 17 Sekunden def height(n, m): arr = [1,1] while m > 1: arr = [1] + list(map(lambda x,y: x+y, arr[1:], arr[:-1])) + [1] m-=1 return sum(arr[1:n+1])
Oder 8, wenn Sie nur das halbe Dreieck zählen def height(n, m): arr = [1,1] while m > 2 and len(arr) < n+2:
Um nicht zu sagen, dass eine optimalere Lösung. Bei einigen Daten funktioniert es schneller, bei einigen langsamer. Wir müssen tiefer gehen. Was ist dieses Dreieck mit Zahlen, die zweimal in der Lösung vorkamen? Es ist eine Schande zuzugeben, aber ich habe die höhere Mathematik, in der das Dreieck gedacht haben muss, sicher vergessen, also musste ich es googeln.
Bingo!
Pascals Dreieck , wie es offiziell genannt wird. Unendliche Binomialkoeffiziententabelle. Die Antwort auf das Problem mit N Eiern und M Würfen ist also die Summe der ersten N Koeffizienten bei der Erweiterung des Newton-Binomials vom M-ten Grad mit Ausnahme der Null.
Ein beliebiger Binomialkoeffizient kann durch die Fakultäten der Zeilennummer und der Koeffizientennummer in der Zeile berechnet werden: bk = m! / (N! * (Mn!)). Das Beste ist jedoch, dass Sie die Zahlen in der Zeichenfolge nacheinander berechnen können, wobei Sie die Anzahl und den Nullkoeffizienten (immer eins) kennen: bk [n] = bk [n-1] * (m - n + 1) / n. Bei jedem Schritt verringert sich der Zähler um eins und der Nenner erhöht sich. Und die prägnante endgültige Lösung sieht folgendermaßen aus:
def height(n, m): h, bk = 0, 1
33 ms zur Berechnung von f (9477, 10000)! Diese Lösung kann auch optimiert werden, obwohl in den angegebenen Bereichen und es funktioniert gut. Wenn n in der zweiten Hälfte des Dreiecks liegt, können wir es in mn invertieren, die Summe der ersten n Koeffizienten berechnen und von 2 ^ m-2 subtrahieren. Wenn n nahe an der Mitte liegt und m ungerade ist, können die Berechnungen auch reduziert werden: Die Summe der ersten Hälfte der Linie beträgt 2 ^ (m-1) -1, der letzte Koeffizient in der ersten Hälfte kann durch Fakultäten berechnet werden, seine Zahl ist (m-1) / 2, und fügen Sie dann entweder weitere Koeffizienten hinzu, wenn sich n in der rechten Hälfte des Dreiecks befindet, oder subtrahieren Sie, wenn sich in der linken Hälfte befindet. Wenn m gerade ist, können Sie die Hälfte der Linie nicht zählen, aber Sie können die Summe der ersten m / 2 + 1-Koeffizienten ermitteln, indem Sie den Durchschnitt durch Fakultäten berechnen und die Hälfte davon zu 2 ^ (m-1) -1 addieren. Bei Eingabedaten im Bereich von 10 ^ 6 reduziert dies die Ausführungszeit sehr deutlich.
Nach einer erfolgreichen Entscheidung begann ich, nach Recherchen anderer zu diesem Thema zu suchen, fand aber in den Interviews nur dasselbe mit nur zwei Eiern, und dies ist kein Sport. Das Internet wird ohne meine Entscheidung unvollständig sein, entschied ich, und hier ist es.