Julia. Bekanntschaft

Ode an Julia

Es ist sehr schwierig, die Begeisterung zu vermitteln, die mit dem Start der ersten Programme und der Korrektur der ersten Fehler in dieser Sprache einherging. Einfach und schön wie Python , ein bisschen wie Fortran , bequemes Arbeiten mit Arrays und Grafiken sowie die Fähigkeit, selbst für Dummies wie z ich meine Klassenkameraden. Sie können auf verschiedenen Abstraktionsebenen arbeiten: Von der Programmierung auf hoher Ebene mit dynamischer Typisierung können Sie zu Assembler-Befehlen übergehen, dh Sie haben sowohl Python-Zugriff als auch die Ausführungsgeschwindigkeit von Fortran-Zählern. Ich kann das Gefühl nicht loswerden, dass Mathcad , Scilab und sogar C ++ in mein Herz verschwinden.

Ich lernte die Sprache, indem ich versehentlich auf eine chabrowische Veröffentlichung stieß , und als beeindruckbarer Schüler sollte ich nach Rat suchen, vorzugsweise auf Russisch. Da sich die Sprache seit sechs Jahren ständig weiterentwickelt, wurden die ohnehin knappen Informationsquellen veraltet und die Aufregung begann abzunehmen. Mit dem Beginn eines neuen Laborkurses zur Modellierung physikalischer Phänomene mit freier Wahl einer Programmiersprache bestand jedoch immer noch die Motivation, Julia kennenzulernen. Außerdem wird im August die Sprache "1.0 addieren" .

Das unten vorgestellte Material war als Einführung in die Sprache geplant, in der alle Laborarbeiten verfasst und ein Schulungshandbuch gesammelt wurden.

Julia ist eine leistungsstarke dynamische Programmiersprache für mathematische Berechnungen. Die Syntax ähnelt der matlab-Familie, die Sprache ist in C , C ++ und Scheme geschrieben , es ist möglich, Sysh-Bibliotheken aufzurufen

Installation

Nun, alles hat sich endlich beruhigt, jetzt zu unserer Verfügung:

• JuliaPRO-Eingabeaufforderung - alle Yulina-Fähigkeiten direkt vom Dolmetscher.
• Juno ist eine schöne IDE mit einem Fenster für Grafiken und einem Arbeitsbereich, in dem Sie den Inhalt aller Objekte anzeigen können
• Jupyter - Startet den Computerkern in der Konsole und Sie können den Code direkt im Browser ausführen. (Neben Julia ist auch Python anwesend)

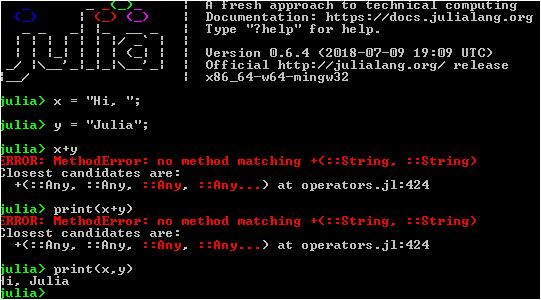
Mal sehen, was dieser Rechner kann ... Unicode-Unterstützung - Sie können das kyrillische Alphabet und Hieroglyphen verwenden und pi den griechischen Buchstaben nennen. Und Sie können die Multiplikation zwischen der Zahl und der Variablen nicht explizit angeben (in dieser Reihenfolge und ohne Leerzeichen):

x = 5+8 2x - 3x + 2x^2 Out: 325 

Alle erforderlichen Zeichen sind ebenfalls vorhanden: + =, * =, >> = usw. (Das Vorzeichen ">>" (Bitverschiebung nach rechts). Vergleichszeichen:>,> =, <, <=, ==,! =. Ungleichungen können zu Ketten zusammengefasst werden:

 y = 5 y += 2 4 <= y < 8 Out: true 

Komplexe Zahlen verfügbar:

 (2-1im)*(4+3im) Out: 11 + 2im 

Und Funktionen für die Arbeit mit ihnen:

• real (z) ist der Realteil,
• imag (z) ist der Imaginärteil,
• konj (z) ist das komplexe Konjugat,
• abs (z) - Modul,
• abs2 (z) ist das Quadrat des Moduls,
• Winkel (z) ist das Argument einer komplexen Zahl.

Sie können rationale Zahlen mit "//" und den entsprechenden Funktionen verwenden:

• num (x) - Zähler,
• den (x) - Nenner,
• float (x) - wird in eine Dezimalzahl konvertiert

 x = 4//6+5//7 Out: 29//21 float(x) Out: 1.380952380952381 

Julia hat die Möglichkeit, die interne Darstellung von Daten zu steuern:

• typeof (obj) - Objekttyp
• typemax (obj) ist die maximale Anzahl dieses Typs
• typemin (obj) - minimal
• eps () - Maschinennullpunkt
• BigInt ist ein großes Ganzes
• BigFloat - großer Gleitkomma

 q = 3 typemax(q) Out: 9223372036854775807 typeof(q) Out: Int64 BigFloat(2.3^45/6) Out: 3.159376405019356000000000000000000000000000000000000000000000000000000000000e+15 

Funktionen

Feature Kit

• abs (x) ist der Modul einer Zahl,
• abs2 (x) ist das Quadrat des Moduls,
• sqrt (x) ist die Quadratwurzel,
• cbrt (x) ist die Kubikwurzel,
• exp (x) ist der Exponent der Zahl,
• log (x) ist der natürliche Logarithmus,
• log10 (x) - Dezimallogarithmus ,
• log (b, x) ist der Logarithmus von x an der Basis b.
  Sowie trigonometrisch, hyperbolisch, Airy, Bessel und viele andere.

Benutzerdefinierte Funktionen:

 function () #  end 

Die Funktion gibt das Ergebnis des letzten Ausdrucks zurück (Mathcad-Benutzer hiccuped).

 function cube(x) x^3 end cube(4) Out: 64 

Nun, oder wir geben ausdrücklich an:

 function myabs(x) if x>=0 return x else return -x end end myabs(-12) Out: 12 

Zurückgegebene Werte können in einem Tupel gesammelt werden:

 function cubeandsquare(x) x^3,x^2 end a,b = cubeandsquare(3) print("a = $a, b = $b") Out: a = 27, b = 9 

Funktionen können Tupel, Standardwerte und Schlüsselwörter annehmen. Wenn nach dem Funktionsnamen keine Klammern stehen, wird er als Variable betrachtet und kann einer anderen Variablen zugewiesen oder als Parameter an die Funktion übertragen werden. Julia unterstützt auch einen funktionalen Stil beim Schreiben von Programmen (Hallo Lisp)

 function mysin(t;A=1,?=1,?=0) #   -     A*sin(?*t + ?) end x1 = mysin(pi) #   = 0 x2 = mysin(pi*0.5,A = 2) #      x3 = mysin(pi*0.5,? = 0.5) #      print("x1 = $x1, x2 = $x2, x3 = $x3") Out: x1 = 1.2246467991473532e-16, x2 = 2.0, x3 = 0.7071067811865475 

Arrays

Als Scilab- Benutzer habe ich die Ersetzung nicht einmal bemerkt: Sie können ein Array mit der folgenden Funktion angeben:

• Array {T} (undef, dims ...) - Ein Array vom Typ T und Dimension dims
• Nullen (T, dims ...) - Array von Nullen
• Einsen (T, Dims ...) - oder Einheiten
  Die Indizierung beginnt mit einem anstelle von $ - end , und alle erforderlichen Operationen für Matrizen werden definiert (um beispielsweise eine elementweise Addition oder Multiplikation durchzuführen, müssen Sie einen Punkt vor den Operator setzen).

(Jetzt ist klar, wie Bilder eingefügt werden, aber okay ...)

Grundfunktionen:

• det (A) - Determinante berechnen
• A ' - transponiere die Matrix
• inv (A) - Matrix invertieren
• Länge (A) - Anzahl der Elemente
• ndims (A) - Anzahl der Dimensionen
• Größe (A) - Tupel der Abmessungen
• Größe (A, n) - Dimension in einer bestimmten Richtung
• copy (A) - Erstellt eine Kopie des Arrays
• Linspace (Start, Ende, Schritt) oder
  linspace (start: step: end) - erstellt ein eindimensionales Array

 A = [1 2 3; 6 5 4; 7 8 9] Out: 3?3 Array{Int64,2}: 1 2 3 6 5 4 7 8 9 A[2,1] Out: 6 A[end] Out: 9 size(A) Out: (3, 3) 

Sie können Teile des Arrays auswählen, indem Sie einen Indexbereich entlang der Dimension mit dem Zeichen ":" angeben.

 m1 = rand(3,2) m2 = reshape(1:2:11, 3,2) Out: 3?2 Base.ReshapedArray{Int64,2,StepRange{Int64,Int64},Tuple{}}: 1 7 3 9 5 11 m3 = [m1 m2] #   (  ) Out: 3?4 Array{Float64,2}: 0.325649 0.701038 1.0 7.0 0.513579 0.620215 3.0 9.0 0.815242 0.805307 5.0 11.0 m5 = [m1; m2] #   (  ) Out: 6?2 Array{Float64,2}: 0.325649 0.701038 0.513579 0.620215 0.815242 0.805307 1.0 7.0 3.0 9.0 5.0 11.0 m3[:, 2:4] Out: 3?3 Array{Float64,2}: 0.701038 1.0 7.0 0.620215 3.0 9.0 0.805307 5.0 11.0 

Hier haben wir rand () verwendet, das ein Array von Zufallszahlen einer bestimmten Dimension zurückgibt, und reshape (), das die Dimension des Arrays in die angegebene ändert.

 for a in A #   a   A end 

oder

 for i in eachindex(A) #     i end 

oder

 for i = 1 : size(A,n) # n -      (..    ) #     i end 

Grafiken

Um Grafiken verwenden zu können, müssen Sie ein Paket aus dem Repository herunterladen, um Folgendes auszuwählen:

• Pkg.add ("Plots")
• Pkg.add ("PyPlot")
• Pkg.add ("Gadfly")
• Pkg.add ("Winston")

Am beliebtesten ist der Pythonic PyPlot . Module werden mit dem Befehl verbunden, zum Beispiel:

 using PyPlot 

Versuchen wir jedoch Gaston mit Gnuplot (separat schwingen).
Geladen vom Gaston.jl Team

  Pkg.add("Gaston") 

Und auf den Punkt gebracht:

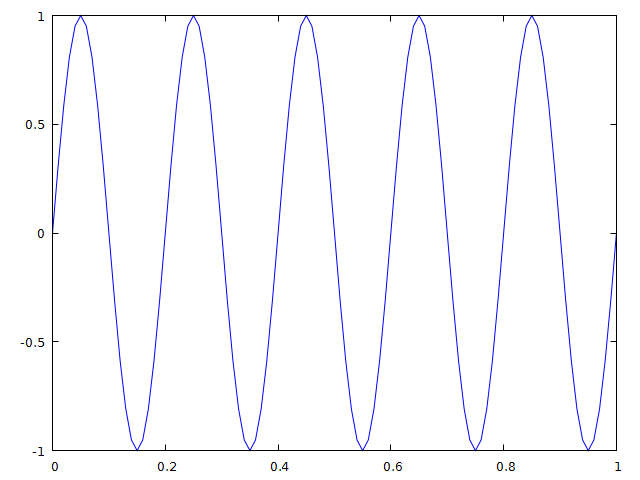
 using Gaston t = 0:0.01:1 plot(t, sin.(2?*5*t)) 

 plot(t,sin.(2?*5*t),title="A sine wave",xlabel="Time (s)",ylabel="Amplitude",grid="on",linewidth=3,color="blue", yrange="[-1.1:1.1]",marker="ecircle",plotstyle="linespoints",linestyle="-.-") 

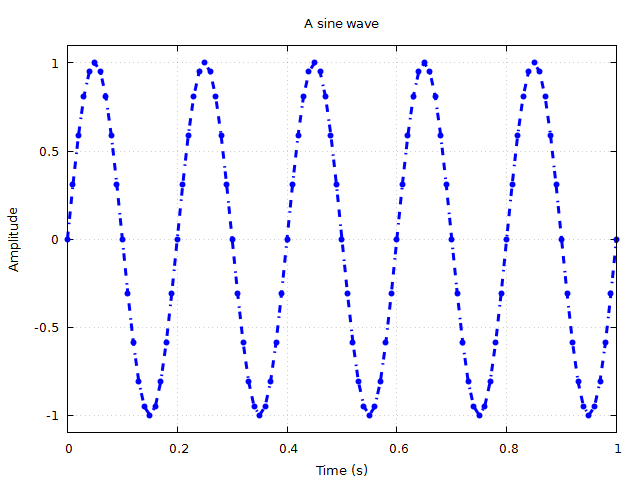
 plot!(t,cos.(2?*5*t),color="red",linewidth=2) #       

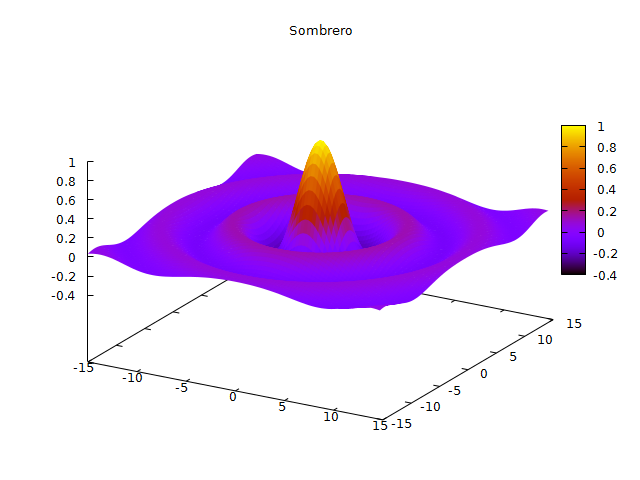
 x = y = -15:0.33:15 surf(x,y,(x,y)->sin.(sqrt.(x.*x+y.*y))./sqrt.(x.*x+y.*y),title="Sombrero",plotstyle="pm3d") 

 x = y = -15:0.33:15 surf(x,y,(x,y)->sin.(sqrt(x.*x+y.*y))./sqrt.(x.*x+y.*y), title="Edge view of a sombrero",plotstyle="pm3d",gpcom="set view 80,20") 

 R = [ x+y for x=0:5:120, y=0:5:120] G = [ x+y for x=0:5:120, y=120:-5:0] B = [ x+y for x=120:-5:0, y=0:5:120] Z = zeros(25,25,3) Z[:,:,1] = R Z[:,:,2] = G Z[:,:,3] = B imagesc(Z,title="RGB Image",clim=[10 200]) 

 histogram(rand(1000),bins=15,norm=1,title="Histogram",yrange="[0:1.6]") 

 y = 1:40 err = Gaston.ErrorCoords(rand(40)) plot(y,err=err,title="Example of error bars",plotstyle="errorbars") 

Mit dem Befehl h = figure () können Sie mehrere grafische Fenster erstellen (funktioniert in Jupyter nicht ) (einfach zwischen Plots einfügen). Verwenden Sie die Befehle, um das Diagramm als Bilddatei zu speichern
set_filename ("name.png") # Wenn nicht angegeben, wird angezeigt
printfigure ("png") # In Datei speichern, PNG, PDF, SVG und GIF verfügbar
Weitere Informationen zum Gaston- Paket

Fazit

Es gibt viel mehr Grafikpakete für jeden Geschmack und für fast alle Bedürfnisse. Außerdem entwickeln sich Hilfspakete mit Macht und Kraft. Hier gibt es Quantencomputer, Bioinformatik, maschinelles Lernen und viele weitere dringende Probleme wie Diffurs und Derivate .

Im Allgemeinen ist Julia schön, klug und sehr vielversprechend, und es ist äußerst unzulässig, sie ohne gebührende Aufmerksamkeit zu lassen.