Dynamische Programmierung oder Teilen und Erobern

Dieser Artikel beschreibt die Ähnlichkeiten und Unterschiede zwischen den beiden Ansätzen zur Lösung algorithmischer Probleme: dynamische Programmierung (dynamische Programmierung) und das Prinzip „Teilen und Erobern“ (Teilen und Erobern). Wir werden als Beispiel zwei Algorithmen vergleichen: die binäre Suche (wie man schnell eine Zahl in einem sortierten Array findet) und die Levenshtein-Entfernung (wie man eine Zeile mit einer minimalen Anzahl von Operationen in eine andere konvertiert).

Ich möchte sofort darauf hinweisen, dass dieser Vergleich und diese Erklärung nicht den Anspruch erheben, äußerst korrekt zu sein. Und vielleicht möchten mich sogar einige Universitätsprofessoren ausschließen :) Dieser Artikel ist nur mein persönlicher Versuch, Dinge zu klären und zu verstehen, was dynamische Programmierung ist und wie das Prinzip „Teilen und Erobern“ involviert ist.

Also, fangen wir an ...

Das Problem

Als ich anfing, Algorithmen zu studieren, war es für mich schwierig, die Grundidee der dynamischen Programmierung (im Folgenden DP aus der dynamischen Programmierung) zu verstehen und zu verstehen, wie sie sich vom Ansatz „Teilen und Erobern“ (weiter DC , Teilen und Erobern) unterscheidet. Wenn es darum geht, diese beiden Paradigmen zu vergleichen, verwenden normalerweise viele erfolgreich die Fibonacci-Funktion, um dies zu veranschaulichen. Und das ist eine großartige Illustration. Mir scheint jedoch, dass wir ein wichtiges Detail verlieren, wenn wir dieselbe Aufgabe zur Veranschaulichung von DP und DC verwenden, um den Unterschied zwischen den beiden Ansätzen schneller zu erkennen. Und dieses Detail ist, dass sich diese beiden Techniken am besten bei der Lösung verschiedener Arten von Problemen manifestieren.

Ich bin noch dabei, DP und DC zu lernen, und ich kann nicht sagen, dass ich diese Konzepte vollständig verstanden habe. Ich hoffe jedoch weiterhin, dass dieser Artikel zusätzliches Licht ins Dunkel bringt und dazu beiträgt, den nächsten Schritt bei der Untersuchung so wichtiger Ansätze wie dynamisches Programmieren und Teilen und Erobern zu unternehmen.

Ähnlichkeiten zwischen DP und DC

So wie ich diese beiden Konzepte jetzt sehe, kann ich schließen, dass DP eine erweiterte Version von DC ist .

Ich würde sie nicht als etwas völlig anderes betrachten. Da beide Konzepte ein Problem rekursiv in zwei oder mehr Teilprobleme desselben Typs aufteilen, bis diese Teilprobleme leicht direkt zu lösen sind. Ferner werden alle Lösungen für das Teilproblem miteinander kombiniert, um letztendlich eine Antwort auf das ursprüngliche, ursprüngliche Problem zu geben.

Warum haben wir dann immer noch zwei verschiedene Ansätze (DP und DC) und warum habe ich dynamische Programmierung als Erweiterung bezeichnet? Dies liegt daran, dass die dynamische Programmierung auf Aufgaben angewendet werden kann, die bestimmte Eigenschaften und Einschränkungen aufweisen . Und nur in diesem Fall erweitert DP DC mithilfe von zwei Techniken: Memoisierung und Tabellierung .

Gehen wir etwas tiefer in die Details ...

Einschränkungen und Eigenschaften, die für die dynamische Programmierung erforderlich sind

Wie wir gerade herausgefunden haben, gibt es zwei Schlüsselmerkmale, die eine Aufgabe / ein Problem haben muss, damit wir versuchen können, es mithilfe dynamischer Programmierung zu lösen:

1. Optimale Unterstruktur - Es sollte möglich sein, eine optimale Lösung für ein Problem aus einer optimalen Lösung für seine Unteraufgaben zusammenzustellen.
2. Überschneidende Teilprobleme - Das Problem muss in Teilprobleme unterteilt werden, die wiederum wiederholt wiederverwendet werden. Mit anderen Worten, ein rekursiver Ansatz zur Lösung des Problems würde eine mehrfache ( nicht eine einzige) Lösung für dasselbe Teilproblem bedeuten, anstatt in jedem rekursiven Zyklus neue und eindeutige Teilprobleme zu erzeugen.

Sobald wir diese beiden Merkmale in dem betrachteten Problem finden, können wir sagen, dass es mit dynamischer Programmierung gelöst werden kann.

Dynamische Programmierung als Erweiterung des Prinzips "Teilen und Erobern"

DP erweitert DC mithilfe von zwei Techniken ( Memoisierung und Tabellierung ), mit denen Lösungen für Teilprobleme für die zukünftige Wiederverwendung gespeichert werden sollen. Daher werden Lösungen nach Teilproblemen zwischengespeichert, was zu einer signifikanten Verbesserung der Algorithmusleistung führt. Beispielsweise ist die zeitliche Komplexität einer "naiven" rekursiven Implementierung der Fibonacci-Funktion O(2 n ) . Gleichzeitig wird eine auf dynamischer Programmierung basierende Lösung in nur (n) .

Das Auswendiglernen (Füllen des Caches von oben nach unten) ist eine Caching-Technik, bei der neu berechnete Lösungen für Unteraufgaben verwendet werden. Die Fibonacci-Funktion, die die Memoisierungstechnik verwendet, würde folgendermaßen aussehen:

 memFib(n) { if (mem[n] is undefined) if (n < 2) result = n else result = memFib(n-2) + memFib(n-1) mem[n] = result return mem[n] } 

Die Tabellierung (Füllen des Caches von unten nach oben) ist eine ähnliche Technik, die sich jedoch in erster Linie darauf konzentriert, den Cache zu füllen und keine Lösung für das Teilproblem zu finden. Die Berechnung der Werte, die zwischengespeichert werden müssen, ist in diesem Fall am einfachsten iterativ und nicht rekursiv durchzuführen. Die Fibonacci-Funktion unter Verwendung der Tabellentechnik würde folgendermaßen aussehen:

 tabFib(n) { mem[0] = 0 mem[1] = 1 for i = 2...n mem[i] = mem[i-2] + mem[i-1] return mem[n] } 

Weitere Informationen zum Vergleich von Memoisierung und Tabellierung finden Sie hier .

Die Hauptidee, die in diesen Beispielen berücksichtigt werden muss, ist, dass wir, da unsere DC-Probleme überlappende Teilprobleme haben, das Zwischenspeichern von Lösungen für Teilprobleme mithilfe einer von zwei Zwischenspeichertechniken verwenden können: Memoisierung und Tabellierung.

Was ist also der Unterschied zwischen DP und DC am Ende?

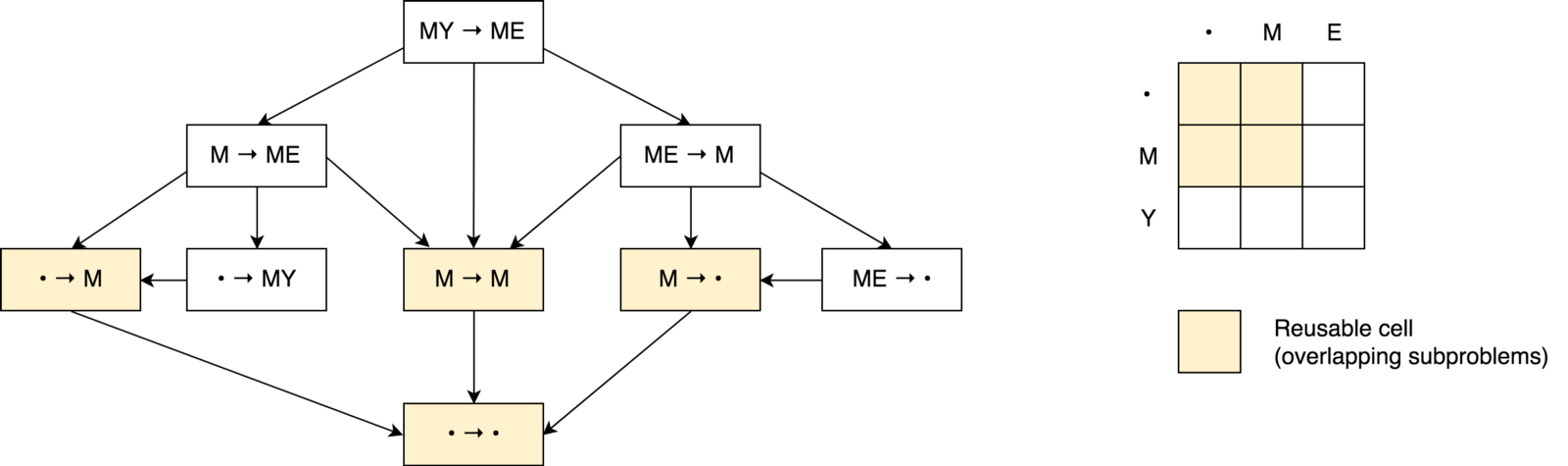
Wir haben die Einschränkungen und Voraussetzungen für die Verwendung der dynamischen Programmierung sowie die im DP-Ansatz verwendeten Caching-Techniken kennengelernt. Versuchen wir, die obigen Gedanken in der folgenden Abbildung zusammenzufassen und darzustellen:



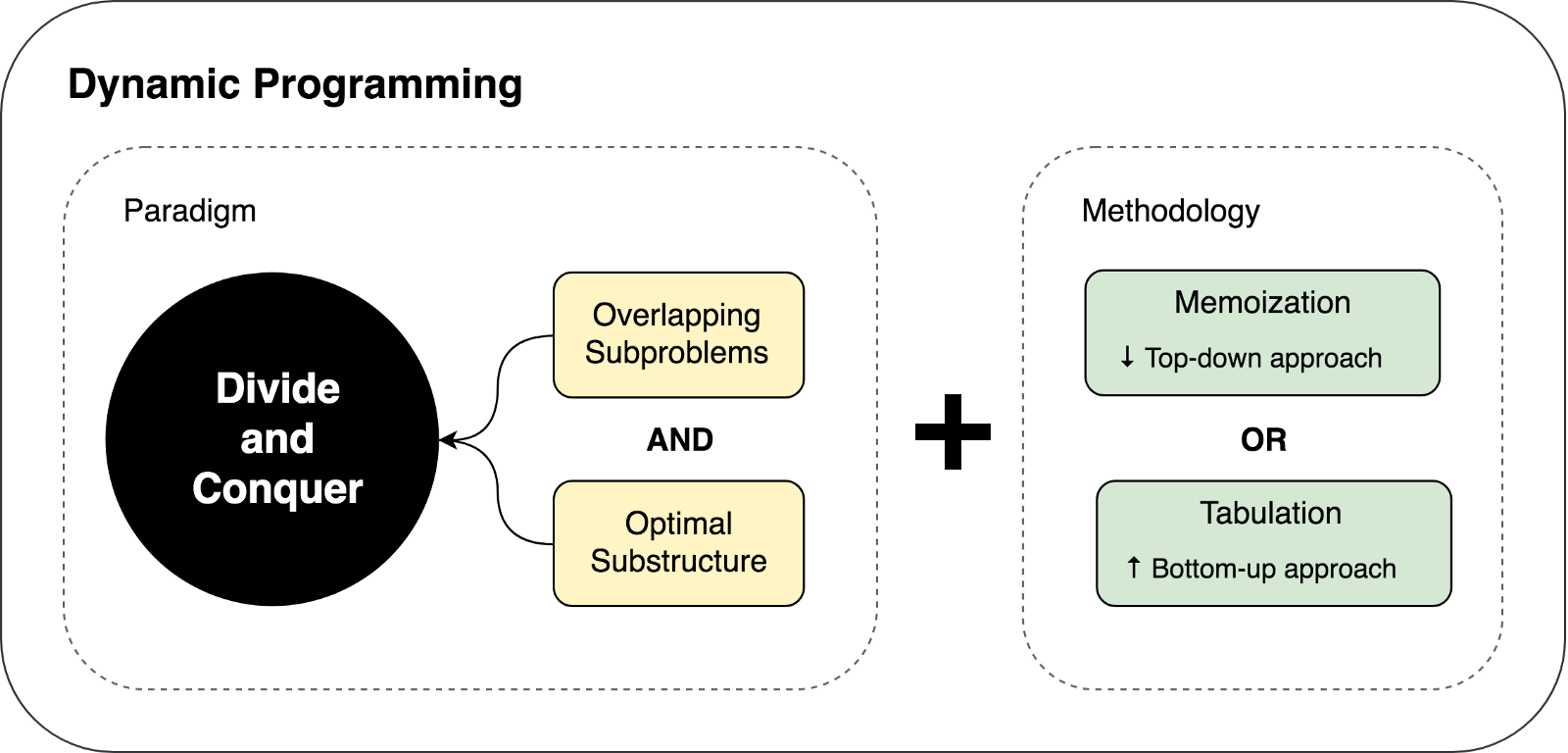
Lassen Sie uns versuchen, einige Probleme mit DP und DC zu lösen, um diese beiden Ansätze in Aktion zu demonstrieren.

Teilen und Erobern Beispiel: Binäre Suche

Der binäre Suchalgorithmus ist ein Suchalgorithmus, der die Position des angeforderten Elements in einem sortierten Array findet. Bei der binären Suche vergleichen wir den Wert der Variablen mit dem Wert des Elements in der Mitte des Arrays. Wenn sie nicht gleich sind, kann die Hälfte des Arrays, in dem sich das gewünschte Element befindet, nicht von der weiteren Suche ausgeschlossen werden. Die Suche wird in der Hälfte des Arrays fortgesetzt, in der sich die gewünschte Variable befinden kann, bis sie gefunden wird. Wenn die nächste Hälfte des Arrays keine Elemente enthält, wird die Suche als abgeschlossen betrachtet und wir schließen daraus, dass das Array nicht den gewünschten Wert enthält.

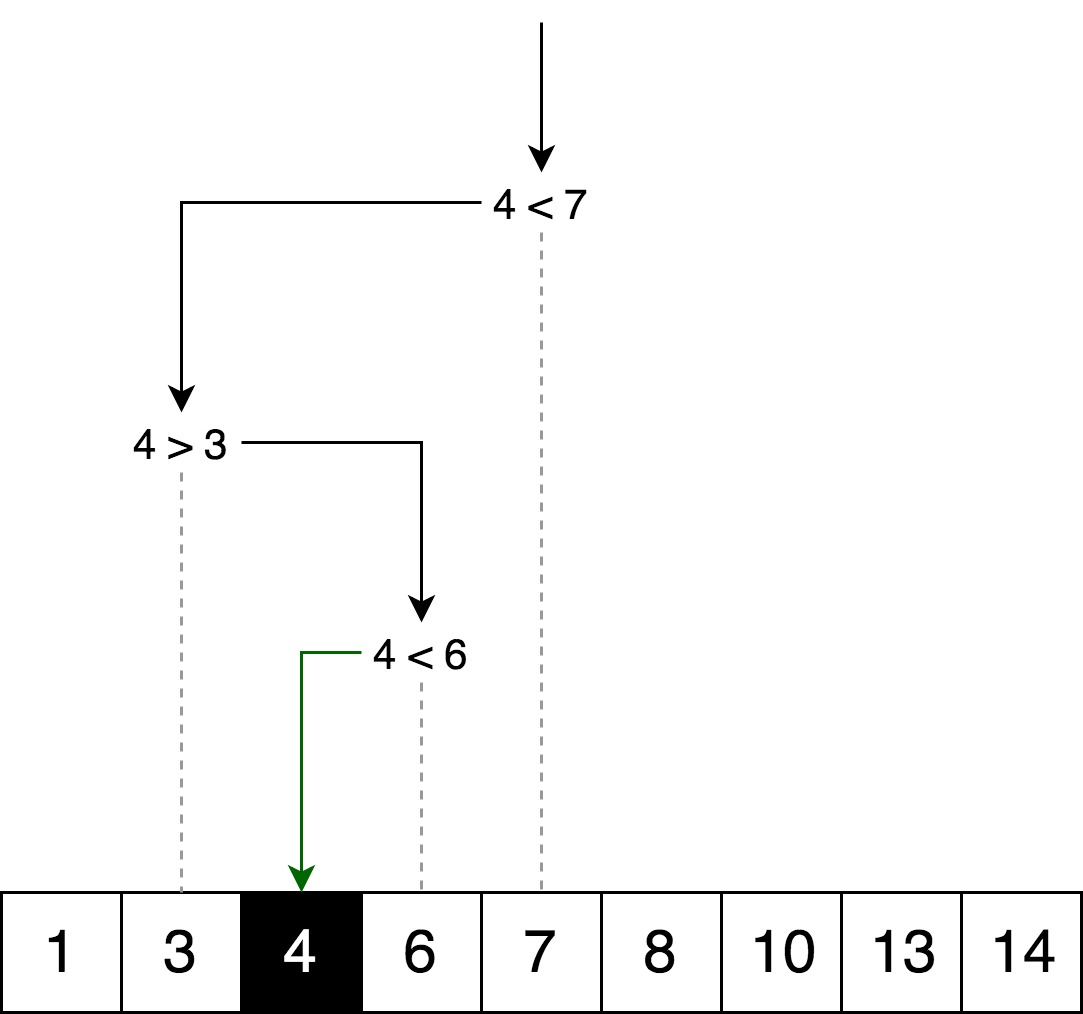
Beispiel

Die folgende Abbildung zeigt ein Beispiel für eine binäre Suche nach der Nummer 4 in einem Array.



Lassen Sie uns dieselbe Suchlogik darstellen, jedoch in Form eines „Entscheidungsbaums“.



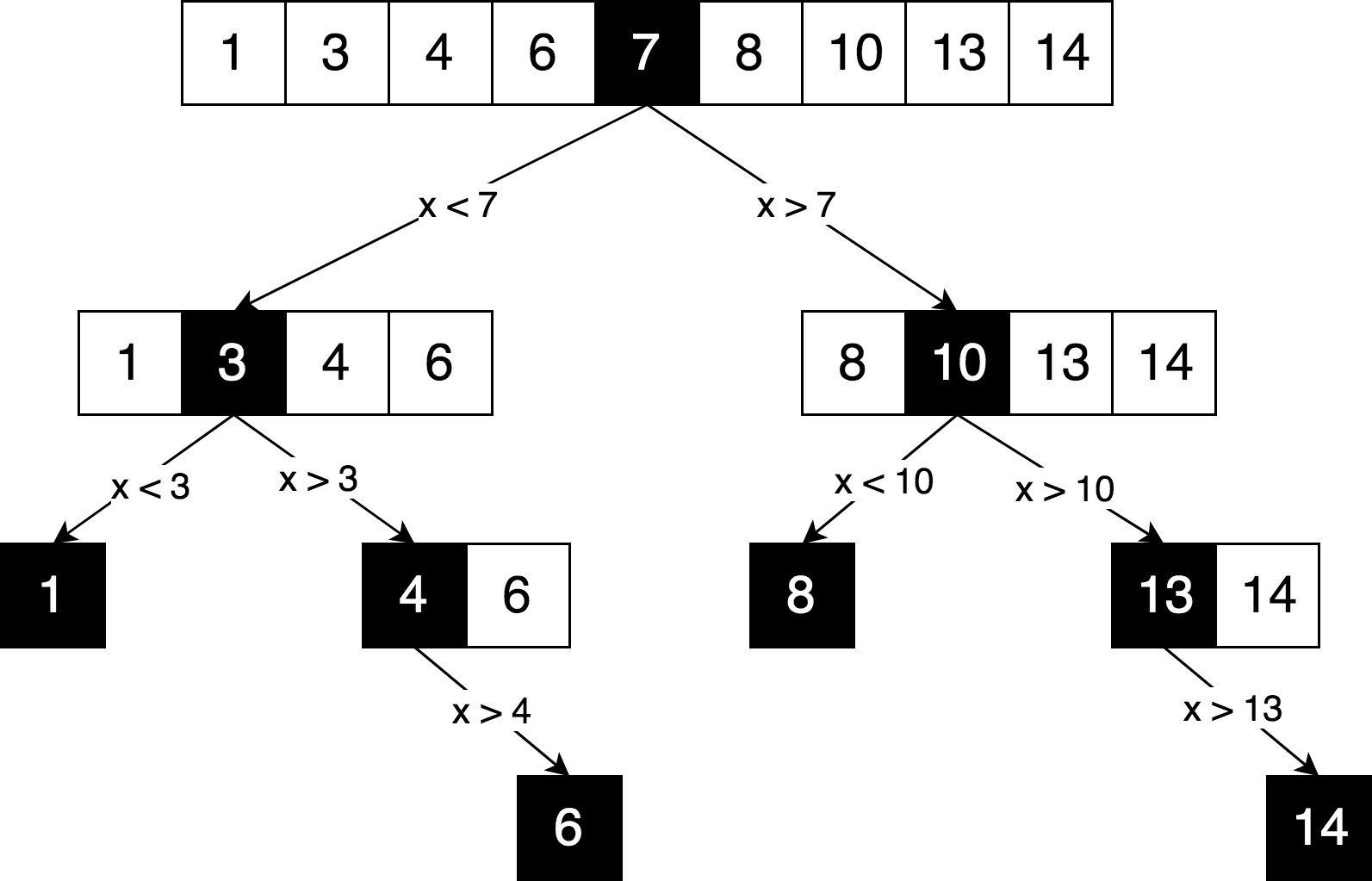
Sie können in diesem Diagramm ein klares Prinzip von "Teilen und Erobern" sehen, das zur Lösung dieses Problems verwendet wird. Wir teilen unser ursprüngliches Array iterativ in Subarrays auf und versuchen, das Element, nach dem wir suchen, bereits darin zu finden.

Können wir dieses Problem mit dynamischer Programmierung lösen? Nein, nein. Aus dem Grund, dass diese Aufgabe keine sich überschneidenden Teilprobleme enthält . Jedes Mal, wenn wir ein Array in Teile aufteilen, sind beide Teile völlig unabhängig und überlappen sich nicht. Und gemäß den oben diskutierten Annahmen und Einschränkungen der dynamischen Programmierung müssen sich Teilprobleme irgendwie überschneiden, sie müssen sich wiederholen .

Wenn ein Entscheidungsbaum genau wie ein Baum aussieht (und nicht wie ein Diagramm ), bedeutet dies normalerweise höchstwahrscheinlich, dass es keine überlappenden Teilprobleme gibt.

Implementierung des Algorithmus

Hier finden Sie den vollständigen Quellcode des binären Suchalgorithmus mit Tests und Erklärungen.

 function binarySearch(sortedArray, seekElement) { let startIndex = 0; let endIndex = sortedArray.length - 1; while (startIndex <= endIndex) { const middleIndex = startIndex + Math.floor((endIndex - startIndex) / 2); // If we've found the element just return its position. if (sortedArray[middleIndex] === seekElement)) { return middleIndex; } // Decide which half to choose: left or right one. if (sortedArray[middleIndex] < seekElement)) { // Go to the right half of the array. startIndex = middleIndex + 1; } else { // Go to the left half of the array. endIndex = middleIndex - 1; } } return -1; } 

Beispiel für eine dynamische Programmierung: Bearbeiten der Entfernung

Wenn es um die Erklärung der dynamischen Programmierung geht, wird normalerweise die Fibonacci-Funktion als Beispiel verwendet. Nehmen wir in unserem Fall ein etwas komplexeres Beispiel. Je mehr Beispiele, desto einfacher ist es, das Konzept zu verstehen.

Der Bearbeitungsabstand (oder der Levenshtein-Abstand) zwischen zwei Zeilen ist die Mindestanzahl von Operationen, um ein Zeichen einzufügen, ein Zeichen zu löschen und ein Zeichen durch ein anderes zu ersetzen, die erforderlich sind, um eine Zeile in eine andere umzuwandeln.

Beispiel

Der Bearbeitungsabstand zwischen den Wörtern "Kätzchen" und "Sitzen" beträgt beispielsweise 3, da Sie drei Bearbeitungsvorgänge (zwei Ersetzungen und eine Einfügung) ausführen müssen, um eine Zeile in eine andere umzuwandeln. Und es ist unmöglich, eine schnellere Konvertierungsoption mit weniger Vorgängen zu finden:

1. Kätzchen → sitten (Ersetzen von "k" durch "s")
2. sitten → sittin (ersetzt "e" durch "i")
3. sittin → sitzend („g“ vollständig einfügen).

Algorithmusanwendung

Der Algorithmus hat eine breite Palette von Anwendungen, zum Beispiel für die Rechtschreibprüfung, optische Erkennungskorrektursysteme, ungenaue Zeichenfolgensuche usw.

Mathematische Definition eines Problems

Mathematisch wird der Levenstein-Abstand zwischen zwei Linien a, b (mit den Längen | a | bzw. |b| ) durch die function lev(|a|, |b|) , wobei:



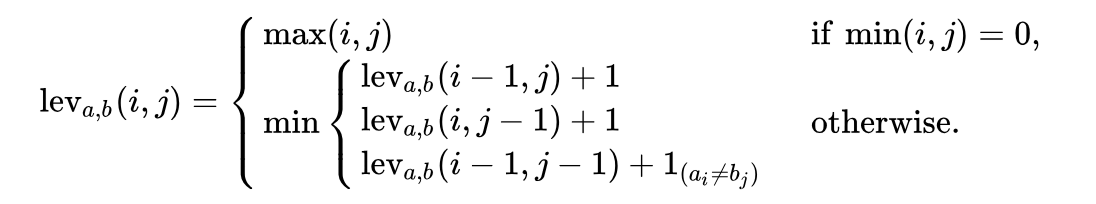
Bitte beachten Sie, dass die erste Zeile in der min Funktion der Löschoperation entspricht, die zweite Zeile der Einfügeoperation und die dritte Zeile der Ersetzungsoperation (falls die Buchstaben nicht gleich sind).

Erklärung

Versuchen wir herauszufinden, was diese Formel uns sagt. Nehmen Sie ein einfaches Beispiel für die Ermittlung des Mindestbearbeitungsabstands zwischen den Zeilen ME und MY . Intuitiv wissen Sie bereits, dass der minimale Bearbeitungsabstand ein ( 1 ) Ersetzungsvorgang ist (ersetzen Sie „E“ durch „Y“). Aber lassen Sie uns unsere Lösung formalisieren und in eine algorithmische Form umwandeln, um komplexere Versionen dieses Problems zu lösen, beispielsweise die Umwandlung des Wortes Samstag in Sonntag .

Um die Formel auf die Transformation ME → MY anzuwenden, müssen wir zuerst den minimalen Bearbeitungsabstand zwischen ME → M, M → MY und M → M ermitteln. Als nächstes müssen wir das Minimum von drei Abständen wählen und eine Operation (+1) der Transformation E → Y hinzufügen.

Wir können also bereits die rekursive Natur dieser Lösung erkennen: Der minimale Bearbeitungsabstand ME → MY wird basierend auf den drei vorherigen möglichen Transformationen berechnet. Wir können also bereits sagen, dass dies ein Divide and Conquer-Algorithmus ist.

Um den Algorithmus weiter zu erläutern, fügen wir unsere beiden Zeilen in eine Matrix ein:



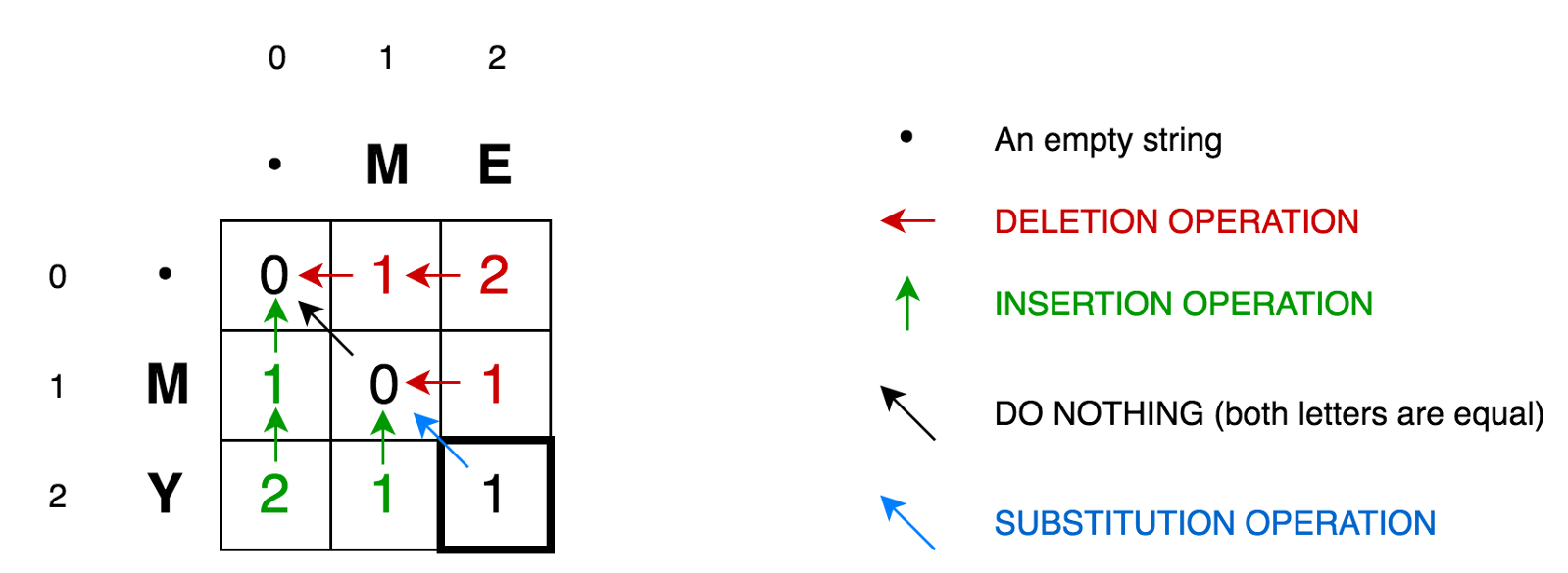Zelle (0,1) enthält die rote Zahl 1. Dies bedeutet, dass wir 1 Operation ausführen müssen, um M in eine leere Zeichenfolge umzuwandeln - löschen Sie M. Daher haben wir diese Zahl rot markiert.

Zelle (0,2) enthält eine rote Zahl 2. Dies bedeutet, dass wir zwei Operationen ausführen müssen, um die Zeichenfolge ME in eine leere Zeichenfolge umzuwandeln - E löschen, M löschen.

Zelle (1,0) enthält eine grüne Zahl 1. Dies bedeutet, dass wir 1 Operation benötigen, um eine leere Zeichenfolge in M ​​- Einfügen M umzuwandeln. Wir haben die Einfügeoperation grün markiert.

Zelle (2,0) enthält eine grüne Zahl 2. Dies bedeutet, dass wir zwei Operationen ausführen müssen, um eine leere Zeichenfolge in eine Zeichenfolge MY umzuwandeln - Y einfügen, M einfügen.

Zelle (1,1) enthält die Nummer 0. Dies bedeutet, dass wir keine Operationen ausführen müssen, um die Zeichenfolge M in M ​​zu konvertieren.

Zelle (1,2) enthält die rote Zahl 1. Dies bedeutet, dass wir 1 Operation ausführen müssen, um den String ME in M ​​- delete E umzuwandeln.

Usw…

Für kleine Matrizen wie unsere (nur 3x3) sieht es nicht schwierig aus. Aber wie können wir die Werte aller Zellen für große Matrizen berechnen (zum Beispiel für eine 9x7-Matrix in der Transformation Samstag → Sonntag)?

Die gute Nachricht ist, dass wir gemäß der Formel nur die Werte von 3 benachbarten Zellen (i-1,j) , (i-1,j-1) (i-1,j) berechnen müssen, um den Wert einer Zelle mit den Koordinaten (i,j) zu berechnen (i-1,j-1) und (i,j-1) . Wir müssen nur den Mindestwert von drei benachbarten Zellen ermitteln und einen (+1) zu diesem Wert hinzufügen, wenn die i-te Zeile und die j-te Spalte unterschiedliche Buchstaben haben.

Sie können also wieder deutlich sehen, wie rekursiv diese Aufgabe ist.



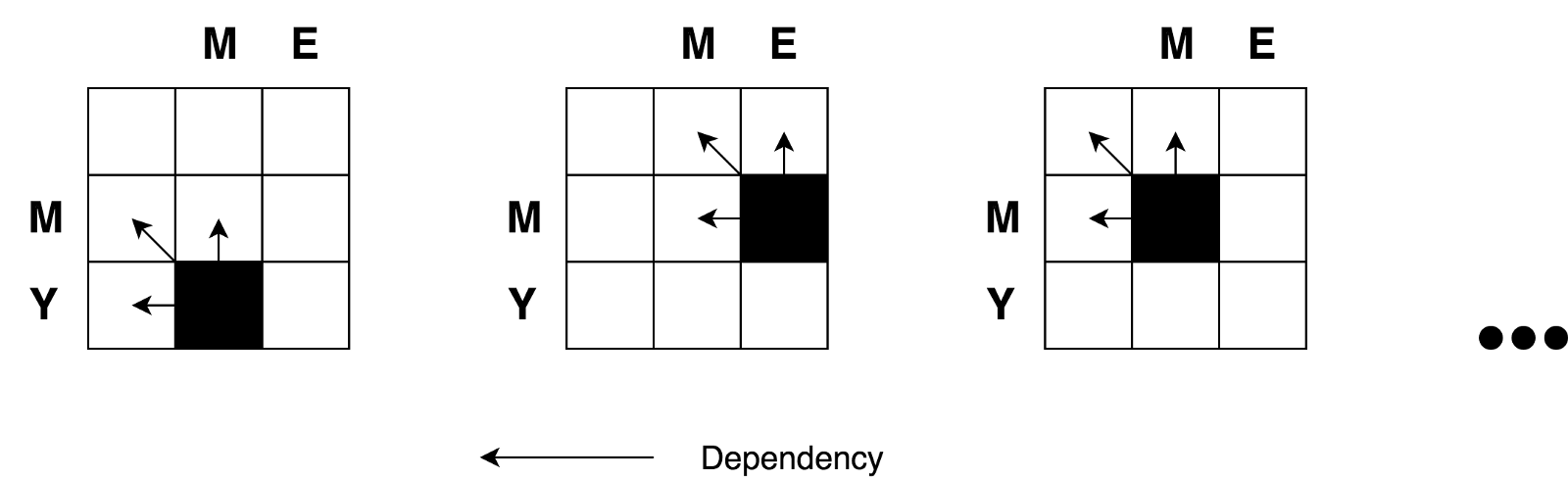
Wir haben auch gesehen, dass wir es mit einer Divide-and-Conquer-Aufgabe zu tun haben. Aber können wir dynamische Programmierung anwenden, um dieses Problem zu lösen? Erfüllt diese Aufgabe die oben genannten Bedingungen für "sich überschneidende Probleme " und " optimale Unterstrukturen "? Ja Lassen Sie uns einen Entscheidungsbaum erstellen.



Zunächst stellen Sie möglicherweise fest, dass unser Entscheidungsbaum eher einem Entscheidungsdiagramm als einem Baum ähnelt . Möglicherweise stellen Sie auch mehrere überlappende Unteraufgaben fest . Es ist auch ersichtlich, dass es unmöglich ist, die Anzahl von Operationen zu reduzieren und sie kleiner als die Anzahl von Operationen aus diesen drei benachbarten Zellen zu machen (Unterprobleme).

Möglicherweise stellen Sie auch fest, dass der Wert in jeder Zelle basierend auf vorherigen Werten berechnet wird. In diesem Fall wird daher die Tabellierungstechnik verwendet (Füllen des Caches in Bottom-Up-Richtung). Sie sehen dies im folgenden Codebeispiel.

Mit all diesen Prinzipien können wir komplexere Probleme lösen, zum Beispiel die Transformationsaufgabe Samstag → Sonntag:



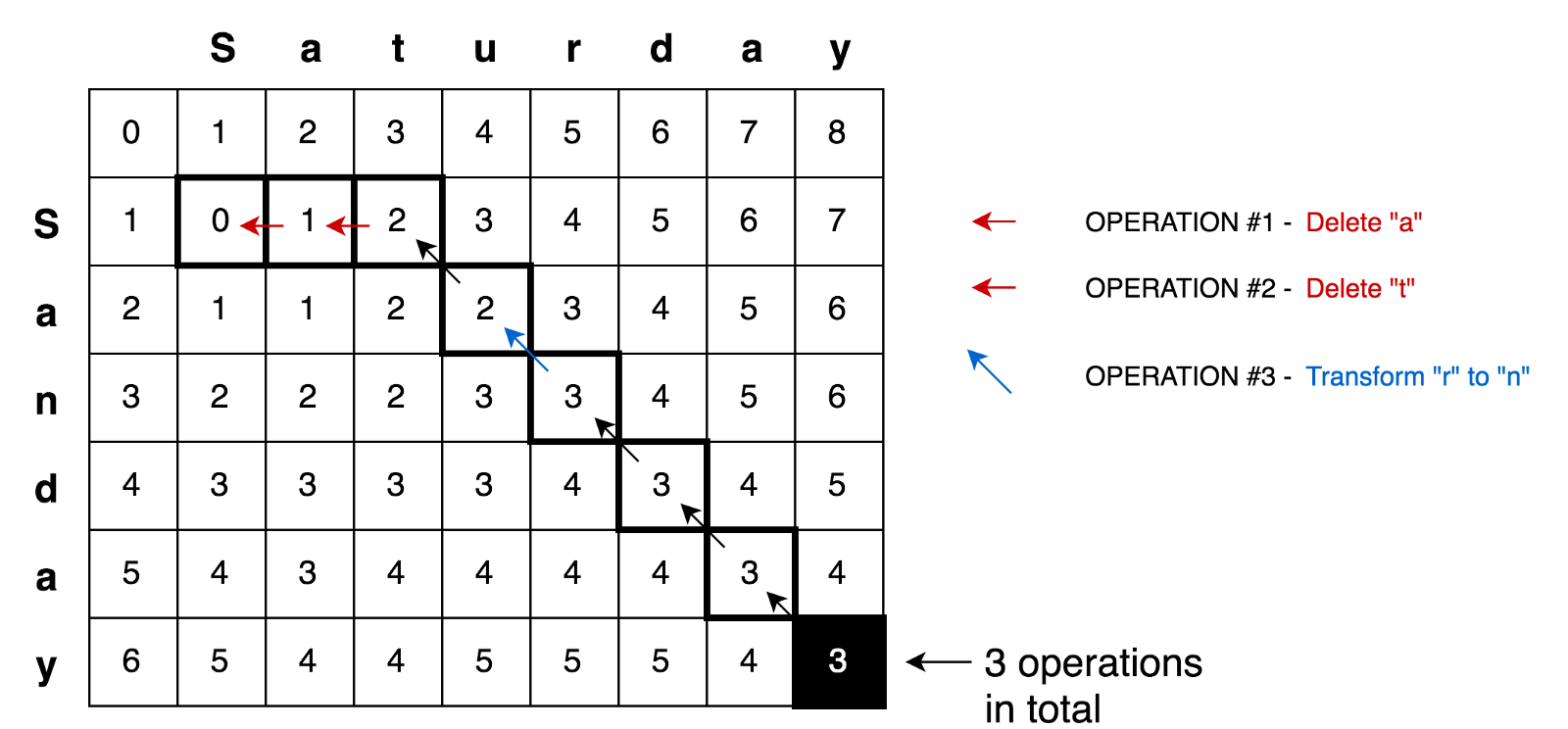Codebeispiel

Hier finden Sie eine Komplettlösung zum Ermitteln des Mindestbearbeitungsabstands mit Tests und Erklärungen:

 function levenshteinDistance(a, b) { const distanceMatrix = Array(b.length + 1) .fill(null) .map( () => Array(a.length + 1).fill(null) ); for (let i = 0; i <= a.length; i += 1) { distanceMatrix[0][i] = i; } for (let j = 0; j <= b.length; j += 1) { distanceMatrix[j][0] = j; } for (let j = 1; j <= b.length; j += 1) { for (let i = 1; i <= a.length; i += 1) { const indicator = a[i - 1] === b[j - 1] ? 0 : 1; distanceMatrix[j][i] = Math.min( distanceMatrix[j][i - 1] + 1, // deletion distanceMatrix[j - 1][i] + 1, // insertion distanceMatrix[j - 1][i - 1] + indicator, // substitution ); } } return distanceMatrix[b.length][a.length]; } 

Schlussfolgerungen

In diesem Artikel haben wir zwei algorithmische Ansätze („dynamische Programmierung“ und „Teilen und Erobern“) mit der Lösung von Problemen verglichen. Wir haben festgestellt, dass die dynamische Programmierung das Prinzip „Teilen und Erobern“ verwendet und zur Lösung von Problemen angewendet werden kann, wenn das Problem sich überschneidende Teilprobleme und die optimale Unterstruktur enthält (wie dies bei der Levenshtein-Distanz der Fall ist). Die dynamische Programmierung verwendet ferner Memoisierungs- und Tabellentechniken, um Unterauflösungen für eine spätere Wiederverwendung beizubehalten.

Ich hoffe, dieser Artikel klärt die Situation für diejenigen unter Ihnen, die versucht haben, sich mit so wichtigen Konzepten wie dynamischer Programmierung und „Teilen und Erobern“ auseinanderzusetzen, anstatt sie zu komplizieren :)

Weitere algorithmische Beispiele mit dynamischer Programmierung mit Tests und Erklärungen finden Sie im Repository für JavaScript-Algorithmen und Datenstrukturen .

Erfolgreiche Codierung!