"Das ist leicht. Wir nehmen die Schwarzschild-Metrik, suchen nach den Christoffel-Symbolen, berechnen ihre Ableitung, schreiben die geodätische Gleichung, ändern einige kartesische Koordinaten (um nicht zu leiden), erhalten eine große mehrzeilige ODE - und lösen sie. Ungefähr so".



Jetzt ist klar, dass die schwarzen Löcher mich gelutscht haben. Sie sind unendlich faszinierend. Das letzte Mal habe ich herausgefunden, wie man die Schwarzschild-Geometrie visualisiert. Ich beschäftigte mich mit dem Problem einer genauen Darstellung, wie sich die Krümmung einer solchen Raumzeit auf das Erscheinungsbild des Himmels auswirkt (da sich Photonen von entfernten Quellen entlang geodätischer Linien bewegen, die von einem Schwarzen Loch gekrümmt werden), um eine interaktive Simulation zu erstellen. Hier ist das Ergebnis (funktioniert im Browser). Der Trick besteht darin, die Berechnung der Abweichung der Lichtstrahlen zu maximieren. Alles funktioniert mehr oder weniger normal, aber natürlich ist eine solche Simulation alles andere als ideal, da dort in Wirklichkeit keine Rückverfolgung erfolgt (für Nichtfachleute: Wiederherstellung der Position von Lichtstrahlen, die in der Zeit in die Kamera fallen).

Mein neues Projekt behebt dieses Manko, indem es auf einfachste Weise auf Effizienz / Interaktivität verzichtet: Dies ist ein Raytracer, der sich ausschließlich auf der CPU befindet . Die Verfolgung wird so genau und so lange wie möglich durchgeführt. Das Rendern des obigen Bildes dauerte auf meinem Laptop 15 bis 5 Minuten (danke, RK4).

Es gibt keine Verbesserung im Vergleich zu ähnlichen Arbeiten. Ich mache es einfach sehr gerne. Ich schreibe diesen Artikel, um nicht nur die Ergebnisse, wie das obige Bild ( zumal andere es besser gemacht haben ), sondern auch den Prozess der Erstellung dieser Bilder mit einer Diskussion / Erklärung der Physik und Implementierung zu teilen. Im Idealfall kann dies Menschen mit ähnlichen Interessen inspirieren oder zu einem Leitfaden werden.

Suchen Sie nach neuen Renderings mit dem Tag starless auf tumlr.

Ein bisschen Pseudo-Riemann-Optik

Schatten

Wenn Sie mein Applet bereits ausprobiert haben, kennen Sie dieses Bild:



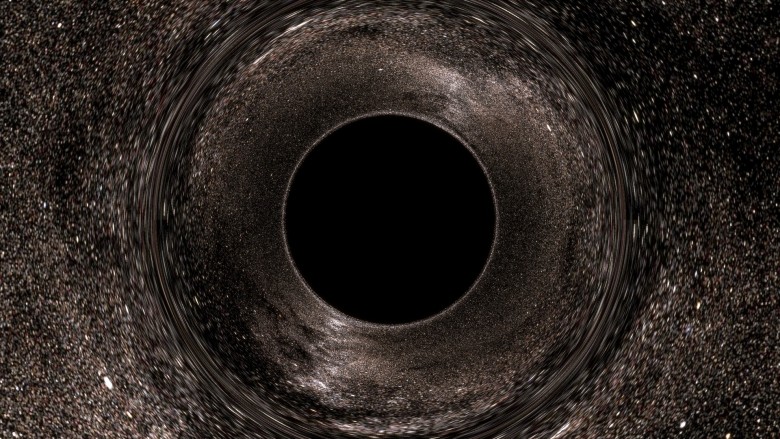
Es hebt die Hauptmerkmale hervor: eine schwarze Scheibe und einen seltsamen Verzerrungsring.

Diskussionen werden oft beachtet: Es ist falsch zu sagen, dass eine schwarze Scheibe ein Ereignishorizont ist. In der Tat ist es falsch zu sagen, dass der Bildbereich ein Objekt ist . Dies ist ein Bild eines Objekts. In der Tat gibt es Trajektorien, die beim Verfolgen von Ihrem Auge zur Quelle im Ereignishorizont (GS) angezeigt werden. Dies sind schwarze Pixel, da kein Photon diesem Weg von einem Schwarzen Loch (BH) zu Ihrem Auge folgen kann. Somit ist diese schwarze Scheibe sehr deutlich ein Bild des Ereignishorizonts in dem Sinne, dass, wenn Sie (in der fernen Vergangenheit) etwas direkt über dem Horizont zeichnen, externe Beobachter es direkt auf dieser schwarzen Scheibe sehen können (wir werden dies tatsächlich ausführen) später experimentieren). In einigen Veröffentlichungen wird diese schwarze Region auch als „Schatten“ von BH bezeichnet.



Es ist jedoch interessant festzustellen, dass dies auch ein Bild der Photonenkugel (PS) ist. Das Gnuplot-Diagramm oben zeigt die Geodäsie eingehender Photonen aus dem Unendlichen (beim Zoomen aus der Ferne auf das BH) sowie GS (schwarz) und FS (grün). Der Radius der Photonenkugel ist 1,5-mal größer als der Radius des Ereignishorizonts (in der Schwarzschild-Geometrie), und hier sind die Kreisbahnen der Photonen um das Schwarze Loch zulässig (obwohl instabil). In der Grafik fallen einige Strahlen in die Nichtexistenz, während andere gestreut werden (und somit an einem anderen Punkt in der Himmelssphäre erscheinen). Es ist ersichtlich, dass für absorbierte Strahlen der Belichtungsparameter weniger als ~ 2,5 Radien beträgt. Dies ist der scheinbare Radius der schwarzen Scheibe und er ist viel größer als der GS und der FS.

In jedem Fall ist folgende Tatsache wichtig:

Ein frei in die Photonenkugel einfallender Lichtstrahl erreicht ebenfalls den Ereignishorizont.

Dies bedeutet, dass das Bild der Photonenkugel im Bild des Ereignishorizonts enthalten ist. Da sich die GS jedoch eindeutig innerhalb der FS befindet, sollte das Bild der ersteren auch eine Teilmenge der letzteren sein. Dann müssen die beiden Bilder übereinstimmen.

Warum überprüfen wir, ob die schwarze Festplatte auch ein Image des FS ist? Denn dies bedeutet, dass der Rand der schwarzen Scheibe mit Photonen gefüllt ist, die entlang der Photonenkugel gleiten . Das Pixel unmittelbar außerhalb der schwarzen Scheibe entspricht einem Photon, das (beim Zurückverfolgen) spiralförmig in die Photonenkugel fällt, näher und näher an eine instabile Kreisbahn, sich viele Male dreht (je näher Sie schauen, desto schneller dreht es sich) und dann spiralförmig auftaucht - da die Umlaufbahn instabil ist - und ins Unendliche entweicht.

Dieses Verhalten verursacht einen interessanten optischen Effekt ähnlich der Separatrix in einem dynamischen System. Wenn der Strahl genau entlang der Kante gestartet wird, dreht er sich theoretisch für immer in einer Spirale, näher und näher an der Kreisbahn der Photonenkugel.

Einfluss auf die himmlische Sphäre

Wir werden uns nicht auf dieses Thema konzentrieren, da das letzte Applet diesem Thema gewidmet ist und eine viel bessere Vorstellung von Verzerrungen am Himmel vermittelt (einschließlich der UV-Gitteroption für klarere Verzerrungen).

Nur ein paar Worte zum Einsteinring. Die Gravitationslinse ist optisch unterscheidbar, da es sich um ein Bild eines einzelnen Punktes handelt, der sich direkt gegenüber dem Betrachter befindet. Der Ring wird in einem solchen Betrachtungswinkel gebildet, wenn die Strahlen des Betrachters parallel gebogen werden. Externe Strahlen sind nicht genug gekrümmt und bleiben divergent; im Inneren biegen sie sich zu stark, konvergieren und können in Wirklichkeit sogar rückwärts oder im Kreis verlaufen, wie wir gesehen haben.

Aber denken Sie darüber nach: Wenn Sie sich der schwarzen Scheibe nähern, können die Lichtstrahlen einen Kreis bilden und dann parallel verlaufen. Dort sollten wir den Einstein-Sekundärring sehen. Tatsächlich kann es Ringe beliebiger Reihenfolge geben (beliebig viele Wicklungen). Zwischen ihnen sollten sich auch „merkwürdige“ Ringe befinden, bei denen sich die Lichtstrahlen parallel biegen, aber auf den Betrachter gerichtet sind. Diese endlose Reihe von Ringen existiert, ist aber in unserem Bild (in den meisten dieser Bilder) völlig unsichtbar, weil sie zu nahe am Rand der Platte liegt.

Verzerrung des Ereignishorizonts

In diesem neuen Bild hat sich etwas geändert. Erstens wird es in besserer Auflösung und mit Hintergrundfilterung erstellt, um die Unterscheidbarkeit zu verbessern. Dann habe ich das BH-Bild vergrößert (wir nähern uns nicht, wir sind immer noch in einem Abstand von ~ 10 Radien davon, nur ein Zoom). Vor allem aber habe ich ein Gitter am Horizont gezeichnet .

Der Horizont ist "nur eine Kugel". Technisch gesehen ist es keine Standard-Riemannsche Kugel mit einer räumlichen Metrik. Der Horizont ist lichtartig! Dies ist eine farbenfrohe Art zu sagen, dass es sich mit Lichtgeschwindigkeit fortbewegt. In den Schwarzschild-Koordinaten ist es jedoch immer noch eine Oberfläche $$$r = 1$ und wir können verwenden $$$\ phi$ und $$$\ theta$ wie Längen- und Breitengrad. Somit kann ein Gitter auf kanonische Weise gezeichnet werden. Sie sehen sie auf dem Bild.

Das Gitter ermöglicht es Ihnen, einen speziellen Effekt zu sehen, der abgeleitet werden kann, wenn wir die Streu- / Absorptionskurve der Photonen oben analysieren:

Die gesamte Oberfläche des Horizonts ist von jedem Punkt aus gleichzeitig sichtbar.

Es ist sehr interessant. Wenn Sie eine feste Kugel in einer normalen flachen Raumzeit betrachten, sehen Sie zu keinem Zeitpunkt mehr als 50% ihrer Oberfläche (wenn Sie sich nähern, sind es aufgrund der Perspektive weniger als 50%). Der Horizont ist aber gleichzeitig mit einer schwarzen Scheibe sichtbar : Achten Sie insbesondere auf den Nord- und Südpol. Obwohl sich die gesamte Oberfläche auf einer schwarzen Scheibe befindet, wird sie nicht vollständig abgedeckt : Wenn Sie den Rand vergrößern, sehen Sie, dass das Bild des GE bis zum Ende des Schattens endet. Sie finden einen Ring sehr nahe am äußeren Rand, aber nicht am Ende. Dieses Bild ist ein Punkt gegenüber dem Betrachter und definiert die Grenzen dieses „ersten“ Bildes des HS im Inneren. Was ist also zwischen diesem Ring und der tatsächlichen Kante? Ich habe noch kein vergrößertes Bild erstellt, aber es gibt noch ein ganzes Bild des Ereignishorizonts . Und dann noch eine und noch eine bis ins Unendliche. Es gibt endlose konzentrische Bilder des gesamten Horizonts, die im Schatten komprimiert sind. (Vielen Dank an / u / xXxDeAThANgEL99xXx für den Hinweis auf dieses Phänomen, das ich verpasst habe) .

Hinzufügen einer Akkretionsscheibe

Was wird ein modernes Rendering von BH ohne eine Akkretionsscheibe tun? Obwohl dies eindeutig eine umstrittene Frage ist, steht Nolans Interstellar wirklich zur Beobachtung zur Verfügung, ganz zu schweigen von der Genauigkeit, aber wir müssen dem Blockbuster definitiv dafür danken, dass er eine bestimmte Verzerrung der Akkretionsscheibe populär gemacht hat. Hier haben wir eine unendlich dünne, flache, horizontale Akkretionsscheibe, die sich von der Photonenkugel aus erstreckt (obwohl dies sehr unrealistisch ist, weil die Bahnen niedriger sind $$$3r_S$ instabil, wie unten beschrieben) bis zu 4 Radien, lackiert in einem weiß-blauen Käfig. Bei einer solchen Farbe ist es offensichtlich, dass wir uns einem anderen Fall gegenübersehen, wenn gleichzeitig 100% der Oberfläche des Objekts sichtbar sind.

Für dieses Bild habe ich den Betrachter etwas höher bewegt, um die Scheibe von oben zu betrachten. Sie sehen Bilder von zwei Seiten der Festplatte : der oberen und der unteren. Das Bild biegt sich in einem Bogen über den Schatten des Schwarzen Lochs, da sich der direkt über das Schwarze Loch gerichtete Strahl nach unten biegt, um die Oberseite der Scheibe hinter dem Loch gegenüber dem Betrachter zu treffen.

Dies erklärt auch die Existenz des unteren Bildes: Die Strahlen, die unter das BH gehen, werden zur unteren Oberfläche der Scheibe gebogen, die sich hinter dem BH befindet. Wenn Sie genau hinschauen, verteilt sich das Bild über den Schatten, aber im oberen Teil ist es viel dünner. Dies entspricht den Lichtstrahlen, die über das BH gehen, einen fast vollen Kreis um das Loch bilden und auf die untere Oberfläche vor der Scheibe treffen.

Natürlich ist es leicht zu schließen, dass es unendlich viele Bilder von Akkretionsscheiben gibt, die sehr schnell dünner werden, wenn sie sich dem Rand nähern. Das nächste Bild ist bereits sehr dünn und im unteren Teil der Kante kaum sichtbar.

GIFs sind weiterhin relevant

In dieser krampfhaften Animation schalte ich die Lichtablenkung (formal Schwarzschild / Minkowski) ein / aus, um einige der Punkte zu klären, über die wir gesprochen haben.





Diese beiden seltsamen Gifs werden auf Wunsch der Leser erstellt. Im ersten Fall kreist der Beobachter in einem Abstand von 10 Radien um ein Schwarzes Loch. Dies sollte nicht als tatsächliche Umlaufbahn verstanden werden, da es in der Realität keine Aberration gibt, wenn man sich in der Umlaufbahn bewegt. Hier ist eine Reihe stationärer BH-Bilder von mehreren Punkten, an denen sich der Betrachter zwischen den Bildern von Ort zu Ort bewegt. Es ist eine "adiabatische" Umlaufbahn, wenn Sie möchten.

Und Stereo ist immer noch relevant

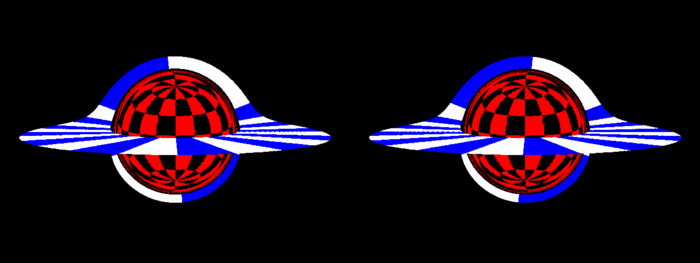
Interessanterweise sieht der Schatten ziemlich flach aus.

Genug der Wissenschaft

Wir haben genug informative Bilder im Stil der 90er Jahre in niedriger Auflösung mit giftigen Farben. Hier sind einige Pop-Renderings (zum Vergrößern anklicken).


Dieses Bild wurde vom Benutzer / n / dfzxh mit vierfacher Überabtastung erstellt


Größerer Plan


Vergrößertes Bild des Rings


Die Kultwirkung des "Lichtrings" von der Äquatorialebene aus gesehen


Wenn Sie das Programm herunterladen, ist dies standardmäßig die aktuelle Szene


Ein viel breiterer Antrieb

Na ja, nichts Besonderes. Es gibt keine Grafik, nur Renderings aus dem Programm. Kehren wir vorübergehend zur Wissenschaft zurück: Das dritte Bild , das keine Bedeutung zu haben scheint, ist tatsächlich sehr wertvoll. Dies ist der vergrößerte Bereich zwischen dem oberen Rand der schwarzen Scheibe und dem Hauptbild der Akkretionsscheibe. Der Betrachter befindet sich am äußeren Rand der Akkretionsscheibe selbst und vergrößert das Bild. Ziel war es, möglichst viele Ringe unterschiedlicher Ordnung darzustellen. Drei Ordnungen sind sichtbar: Die hellere Zone im oberen Teil ist nur der untere Rand des ersten Bildes der oberen fernen Oberfläche der Scheibe. Die Leiste unten unter dem ruhigen Meer gestreckter Sterne ist der obere Teil des Bildes der unteren Vorderseite der Scheibe. Ganz unten - eine dünne Lichtlinie mit einer Breite von nicht mehr als einem Pixel, die auf die schwarze Scheibe der Photonenkugel geklebt ist. Dies ist im Grunde das dritte Bild: wieder die obere entfernte Oberfläche, aber nachdem das Licht eine zusätzliche Umdrehung um das Schwarze Loch vollendet hat. Mit ihm verschmolzen, aber immer dünner werden Bilder Ringe höherer Ordnung. Nun, dies verdient auch das <blockquote> -Tag:

Es gibt endlose Bilder sowohl der oberen als auch der unteren Oberfläche der Akkretionsscheibe, und alle zeigen gleichzeitig die gesamte Oberfläche der Akkretionsscheibe. Darüber hinaus passieren diese Bilder bis auf das allererste weder vor der schwarzen Scheibe noch voreinander und sind daher „konzentrisch“.

Wunderbar.

Ich akzeptiere Rendering-Anfragen
Sie interessieren sich für eine bestimmte Visualisierung, sind aber nicht bereit, die Schwierigkeiten bei der Installation des Programms und beim Rendern selbst zu bewältigen? Schreiben Sie mir einfach einen Reddit oder mailen Sie mir . Das Rendern von 1080p auf meinem Laptop dauert nicht länger als 10 bis 20 Minuten.

Realistische Akkretionsscheibe

Die Akkretionsscheibe in den Renderings ist ziemlich bunt. Es ist nur eine blöde Texturscheibe. Was passiert, wenn die reale Physik im visuellen Erscheinungsbild einer Festplatte enthalten ist? Was passiert zum Beispiel, wenn Sie die Rotverschiebung von der Orbitalbewegung betrachten?

Ein beliebtes Modell einer Akkretionsscheibe ist eine unendlich dünne Materiescheibe in einer fast kreisförmigen Umlaufbahn. Es beginnt mit ISCO (der innersten stabilen Kreisbahn, $$$3r_s$ ) mit einem Temperaturprofil nach einem Potenzgesetz $$$(T \ sim r ^ {- a}$ . Ich werde eine sehr einfache Option verwenden:

$$

$$T \ sim r ^ {- 3/4}$$

Das ist definitiv abnormal in der allgemeinen Relativitätstheorie für realistische Flüssigkeiten, aber hier ist es (auf jeden Fall werden Sie den Unterschied nicht bemerken).

Jetzt ist ein freier Parameter eine übliche Skala für Temperaturen, zum Beispiel die Temperatur in ISCO. Diese Temperatur ist für die meisten Schwarzen Löcher enorm . Wir sprechen von Hunderten Millionen Kelvin; Es ist schwer vorstellbar, dass ein menschliches Artefakt bei solchen Temperaturen unter dem Einfluss von Scheibenstrahlung (Peak in der Röntgenstrahlung) existieren könnte, ganz zu schweigen von der Fotografie. Wir müssen also die Temperatur deutlich senken. Offensichtlich sind supermassereiche Schwarze Löcher kälter, aber nicht genug. Wir müssen in ISCO auf 10.000 K fallen, damit wir zumindest etwas sehen können. Das ist sehr ungenau, aber das ist alles, was ich tun kann.

Es sollten zwei Fragen gestellt werden. Erstens: Welche Farbe hat der schwarze Körper bei dieser Temperatur? Zweitens: Wie hell ist es ? Formal liegt die Antwort auf diese beiden Fragen im Skalarprodukt von Funktionen, die die Kanäle R, G, B mit dem Schwarzkörperspektrum beschreiben. In der Praxis werden einige Näherungswerte verwendet.

Die Formel von Tanner Helland ist für Farben genau und effektiv, enthält jedoch zahlreiche Bedingungen, die mit meiner Raytracing-Funktion nicht realisierbar sind (siehe unten für weitere Einzelheiten). Der schnellste Weg ist die Verwendung einer einfachen Textur:



Diese Textur ist eines von vielen nützlichen Dingen in Mitchell Charitys Auswahl von "Welche Farbe hat der schwarze Körper?" . Als Referenz entspricht es dem Weißpunkt E (Weißpunkt E).

Die Skala zeigt die Farbe eines schwarzen Körpers bei Temperaturen von 1000 K bis 30 000 K, wobei höhere Temperaturen etwa dem gleichen Blauton entsprechen. Da es einen großen Helligkeitsunterschied zwischen den Temperaturen gibt, kann und kann diese Textur keine Helligkeit übertragen. Vielmehr normalisiert es Farben. Unsere Aufgabe ist es, die relative Helligkeit zu berechnen und anzuwenden. Hierfür eignet sich eine analytische Formel. Wenn wir annehmen, dass das sichtbare Spektrum sehr eng ist, ist die gesamte sichtbare Intensität proportional zum Spektrum des schwarzen Körpers selbst:

$$

$$\ frac {1} {\ lambda ^ 5} \ frac {1} {\ exp (\ frac {hc} {\ lambda k_B T}) - 1}$$

wo ich dumme gemeinsame Konstanten losgeworden bin (wir werden immer noch die Helligkeit skalieren, um etwas zu sehen). Sie können einfach einfügen $$$\ lambda$ ungefähr für den sichtbaren Bereich des Spektrums, und wir erhalten, dass die Helligkeit proportional zur Temperatur gemäß dieser Formel ist:

$$

$$(e ^ {\ frac {29622.4 \ text {K}} {T}} - 1) ^ {- 1}$$

Es ist ganz einfach. Zur Kontrolle stellen wir fest, dass die relative Intensität schnell auf Null abfällt, wenn T gegen Null geht, und sich praktisch nicht ändert, wenn T gegen unendlich geht.

Rotverschiebung

In der Beschreibung des Applets haben wir die Orbitalgeschwindigkeiten in der Schwarzschild-Geometrie diskutiert. Zur Berechnung der Rotverschiebung wird die Rotverschiebungsformel aus der SRT verwendet:

$$

$$(1 + z) _ \ text {Doppler} = \ frac {1 - \ beta \ cos (\ theta)} {\ sqrt {1- \ beta ^ 2}}$$

Wo als $$$\ cos (\ theta)$ - der Kosinus des Winkels zwischen der Richtung des von der Scheibe emittierten Strahls und der lokalen Geschwindigkeit der Scheibe, berechnet im lokalen Trägheitskoordinatensystem von Schwarzschild. Die Formel ist in diesem Zusammenhang aufgrund des Äquivalenzprinzips wahr.

Es muss mit dem Rotverschiebungskoeffizienten der Gravitation multipliziert werden:

$$

$$(1 + z) _ \ text {Gravitation} = (1 - r ^ {- 1}) ^ {- 1/2}$$

Dieser Koeffizient hängt nicht von der Flugbahn des Lichtstrahls ab, sondern nur vom Radius der Strahlung, da die Schwarzschild-Geometrie stationär ist.

Dies bedeutet auch, dass der Beitrag der Position des Beobachters zur Rotverschiebung der Gravitation über das gesamte Sichtfeld konstant ist. Unser gesamtes Bild hat eine konstante allgemeine Blauverschiebung, weil wir tief in BH sind. Daher ergibt dieser Effekt nur einen schwachen Farbton, der ignoriert werden kann.

Wir vernachlässigen auch die Rotverschiebung von der Bewegung des Beobachters, weil unser Beobachter in der Schwarzschild-Geometrie stationär ist. Hier ist das Endergebnis:



Wie Sie sehen können, ist der größte Teil der Disc aufgrund der maximalen Helligkeit in den Farbkanälen vollständig weiß. Wenn Sie diese Kanäle auf den Bereich von 0,0 bis 1,0 absenken, werden die äußeren Teile der Festplatte blass oder schwarz.Der Helligkeitsanstieg ist zu groß, um gesehen und geschätzt zu werden. Ich habe versucht, den Effekt mithilfe der Nachbearbeitung zu zeigen, sodass die hellsten Teile einen Farbübergang aufweisen, dies reicht jedoch kaum aus.

Ziemlich verwirrendes Bild. Hier ist ein Bild ohne Berücksichtigung der Helligkeit, in dem Sie die Farben bewerten können:



Diese Bilder haben eine niedrigere Auflösung, da sie auf meinem Laptop sehr lange gerendert werden (Quadratwurzeln sind schlecht, Kinder).

In jedem Fall ist dieser Render tausendmal weniger spektakulär als die anderen (hauptsächlich, weil der innere Rand der Platte bereits weit genug vom GS entfernt ist, sodass die Linse zu groß ist), aber der Render ist zumindest genau . Wenn Sie ein Schwarzes Loch mit einer Temperatur von 10.000 K und einer guten Sonnenbrille finden, werden Sie genau das sehen.

Noch eine Nahaufnahme. Ich habe die Sättigung für Schönheit unnatürlich erhöht:

Schreiben eines Raytracers für ein Schwarzes Loch

Github-Quelle

Es gibt einen sehr großen und offensichtlichen Unterschied zwischen der Optik der Schwarzen Löcher und dem numerischen Integrator, der wunderschöne Desktop-Hintergründe mit einer Auflösung von 1080p erzeugt. Das letzte Mal habe ich meine Argumentation nicht veröffentlicht, sondern einfach ein großes und schmutziges Git-Repository erstellt. Jetzt möchte ich etwas ausführlicher erklären und auch versuchen, den Code in einer genaueren Form und mit Kommentaren zu pflegen.

Mein Tracer wurde nicht gut, kraftvoll und schnell erstellt. Zunächst wollte ich, dass es einfach einzurichten und zu vereinfachen ist, damit die Menschen Inspiration erhalten und das Verbesserungspotenzial erkennen können: Selbst seine Unvollkommenheit kann jemanden dazu ermutigen, sich für das Schreiben einer eigenen Version zu entscheiden. Hier finden Sie eine kurze Übersicht über die Algorithmen und deren Implementierung.

"Magisches" Potenzial

Also, die allgemeine Relativitätstheorie, alles ist klar. Das ist leicht. Wir nehmen die Schwarzschild-Metrik, suchen nach den Christoffel-Symbolen, berechnen ihre Ableitung, schreiben die geodätische Gleichung auf, ändern einige kartesische Koordinaten, um endloses Leiden zu vermeiden, erhalten eine riesige mehrzeilige ODE und lösen sie. Ungefähr so.

Nur ein Scherz. Natürlich gibt es einen Trick.

Wenn Sie sich erinnern, habe ich das letzte Mal die folgende Gleichung für die Umlaufbahn eines masselosen Teilchens in seiner Umlaufbahn in der Schwarzschild-Geometrie abgeleitet ($$u = 1 / r ):$u=1/r$

$$

$$u''(\phi) + u = \frac{3}{2} u^3$$

Der Trick besteht darin, die Binet-Formel hier zu sehen . Für eine Masse eines Newtonschen Teilchens im Newtonschen Potential des Feldes der zentralen Kräfte:

$$

$$\frac{d^2}{dt^2} \vec x = \frac{1}{m} F(r)$$

dann bewegt sich das Teilchen offensichtlich in seiner Orbitalebene und entspricht der Binet-Formel für $$$u(\phi)$ ::

$$

$$u'' + u = - \frac{1}{m h^2 u^2} F(u)$$

Wo $$$\frac{d}{d\phi}$ Ist eine Primzahl $$$m$ - Masse und $$$h$- Drehimpuls pro Masseneinheit. Dies ist eine Gleichung für die Umlaufbahn, keine Bewegungsgleichung. Es sagt nichts darüber aus$$$u(t)$ oder $$$phi(t)$ zeigt nur die Beziehung zwischen $$$u$ und $$$\phi$ .

Lassen Sie uns einen Moment innehalten, um darüber nachzudenken, was wir tatsächlich haben. Die Gleichung besagt, dass, wenn Sie sich ein hypothetisches mechanisches System eines Teilchens unter Einwirkung einer bestimmten Zentralkraft vorstellen, seine Flugbahn eine Lösung der Binet-Formel ist. Dann wird das mechanische System zum Formelrechner.

Das biete ich hier an. Wir haben angegeben$$$m=1$ und sie nahmen (nicht physikalisch, was auch immer) ein einfaches System eines Punktteilchens in diesem speziellen Kraftfeld:

$$

$$\vec F(r) = - \frac{3}{2} h^2 \frac{\hat r}{r^5}$$

wo $$$h$Ist eine bestimmte Konstante, und das numerische Lösen der Gleichung ist sehr einfach. Dann die Lösung$$$\vec x (T)$ wo $$$T$ - Die abstrakte Zeitkoordinate für dieses System ist in der Tat die Parametrisierung der einzigen Lösung für die entsprechende Binet-Gleichung, die genau die geodätische Gleichung ist .

Daher lösen wir die Newtonsche Gleichung in kartesischen Koordinaten, was im Allgemeinen die einfachste ist (ich habe mich für die Runge-Kutta-Methode entschieden, um die Schrittgröße zu erhöhen und die Renderzeit zu verkürzen, aber in Zukunft kann der Benutzer eine andere Lösungsmethode wählen). Dann bekommen wir nur die eigentliche lichtähnliche Geodäsie, wo $$$T$ Geht der Parameter mit (im Gegensatz zum Schwarzschild)? $$$t$ und von der normalen Zeit, die nicht existiert).

Dies ist viel besser als die vorherige Methode, bei der mit Polarkoordinaten in der Umlaufbahnebene gearbeitet wurde. Hier sind die Berechnungen sehr effizient.

Ray Tracing in Numpy

Wenn Sie sich die Quelle ansehen, sehen Sie ein Python-Skript. Horror! Warum Raytracing in Python schreiben? Jeder weiß, wie langsam Schleifen in Python laufen, was der Arbeit immer (fast) ein Ende setzt. Tatsache ist, dass wir Berechnungen in Numpy durchführen - und parallel. Aus diesem Grund kann dieses Programm die bereits gezeichneten Teile nicht schrittweise auf dem Bildschirm anzeigen: Es wird alles gleichzeitig gerendert.

Zunächst erstellen wir eine Reihe von Anfangsbedingungen. Zum Beispiel ein Array (numPixel, 3) mit Vektoren für alle Pixel im Bild (numPixel - Bildbreite × Bildhöhe). Dann wird die Berechnung jedes Strahls auf Arrays des Typs (numPixel, ...) reduziert. Da Operationen mit Arrays in Numpy sehr schnell sind und hier alles statisch typisiert ist (ich hoffe, ich sage im Moment nichts Dummes), sollte es schnell genug berechnet werden. Vielleicht ist es nicht C, aber immer noch schnell. Gleichzeitig haben wir die Flexibilität und Klarheit von Python.

Diese Methode eignet sich hervorragend für die Standard-Strahlverfolgung, bei der Objekte diffuse, reflektierende und brechende Teile aufweisen und es wichtig ist, die Lichtverhältnisse zu berücksichtigen. Beispielsweise ist die selektive Reflexion von Teilen einer Reihe von Strahlen ein wahrer Albtraum. Das Verfolgen von Booleschen Werten oder Schleifenindizes erfordert mehrere Masken, und Schleifen können nicht unterbrochen werden. Aber hier ist ein anderer Fall: Alle Objekte in unserer Szene senden nur Licht aus: den Himmel, eine heiße Akkretionsscheibe, einen pechschwarzen Ereignishorizont und hellen Staub. Sie werden vom einfallenden Licht nicht beeinflusst, und das Licht selbst tritt auch ruhig durch sie hindurch, außer um die Intensität zu verringern. Dies führt uns zu einem Algorithmus zur Bestimmung der Farbe:

Farbmischung

Das ist ganz einfach: Sie müssen nur alle Objekte zwischen uns und der Quelle des Strahls mit ihren entsprechenden Alpha-Werten mischen und übereinander legen, wo sich das am weitesten unten liegende befindet. Wir initialisieren den Farbpuffer mit alpha-transparentem Schwarz. Wenn wir uns dann mit dem Objekt überschneiden, aktualisieren wir den Puffer, indem wir die Farbe aus dem Objekt unter unserem Farbpuffer mischen. Wir führen die gleichen Schritte für Staub durch (verwenden Sie das Dichteprofil $$$r ^ {- 2}$ ) und iteriere weiter bis zum Ende. Beachten Sie, dass der Alpha-Kanal auch als Z-Puffer fungiert, da das Objekt keinen Beitrag mehr leistet, nachdem der Strahl das undurchsichtige Objekt passiert hat (wodurch der Alpha-Wert des Puffers auf 1,0 gesetzt wird).

Der offensichtliche Nachteil dieser Methode besteht darin, dass Sie die Strahlverfolgung nach der Berechnung nicht stoppen können, da sie Teil des Arrays ist, in dem die Verfolgung anderer Strahlen fortgesetzt wird. Zum Beispiel wandern die Strahlen nach einer Kollision mit dem Horizont weiter zufällig, nachdem sie in eine Singularität gefallen sind. Sie können sehen, was passiert, wenn Sie das Horizontobjekt explizit ausschalten. Der Alpha-Mischalgorithmus stellt sicher, dass sie das endgültige Bild nicht beeinflussen, diese Strahlen jedoch die CPU weiterhin belasten.