Ich mache die Leser von Habr weiterhin mit den Kapiteln aus seinem Buch "Theorie des Glücks" mit dem Untertitel "Mathematische Grundlagen der Gesetze der Gemeinheit" vertraut. Dieses populärwissenschaftliche Buch ist noch nicht veröffentlicht und erzählt sehr informell, wie Mathematik es Ihnen ermöglicht, die Welt und das Leben der Menschen mit einem neuen Grad an Bewusstsein zu betrachten. Es ist für diejenigen, die sich für Wissenschaft interessieren und für diejenigen, die sich für das Leben interessieren. Und da unser Leben komplex und im Großen und Ganzen unvorhersehbar ist, liegt der Schwerpunkt des Buches hauptsächlich auf der Wahrscheinlichkeitstheorie und der mathematischen Statistik. Hier werden Theoreme nicht bewiesen und die Grundlagen der Wissenschaft nicht gegeben, dies ist keineswegs ein Lehrbuch, sondern das, was man Freizeitwissenschaft nennt. Aber genau dieser fast spielerische Ansatz ermöglicht es uns, Intuition zu entwickeln, Vorlesungen für Studenten mit anschaulichen Beispielen aufzuhellen und schließlich Nicht-Mathematikern und unseren Kindern zu erklären, dass wir in unserer trockenen Wissenschaft so interessante Dinge gefunden haben.In diesem Kapitel werden wir Geld, Märkte und Entropie diskutieren und auch animierte Gifs betrachten, die leider nicht in einem Buch gedruckt werden können.
Hongren Beobachtung:
Unter Ökonomen wird die reale Welt oft als Sonderfall angesehen.
Wirtschaft ist eine große, ernsthafte, aber eigenartige Wissenschaft. Zweifellos ist es als Disziplin, die das wahre und wichtige Phänomen unserer Welt untersucht, von entscheidender Bedeutung: die wirtschaftliche Realität. Die Wirtschaftswissenschaft strebt nach Beweisbarkeit und Formalisierung, sie hat viel Mathematik, manchmal komplex und interessant. Wenn Sie jedoch ein seriöses wirtschaftliches Lehrbuch öffnen, werden Sie höchstwahrscheinlich einige relativ einfache Berechnungen, vorgefertigte Rezepte und eine Reihe informeller Argumente in diesem Sinne finden: „Aber tatsächlich kann alles falsch sein und im Allgemeinen, wie Sie möchten, wenn dies geschieht der Wille der Hauptakteure oder der Regierung. “ Am Ende kann man das Gefühl bekommen, dass Intuition, Kenntnisse der Psychologie und die Fähigkeit, den allgemeinen Kontext wahrzunehmen, in dieser Disziplin wichtiger sind als genaue Berechnung und sorgfältige Berücksichtigung von Details (es geht um Wirtschaft, nicht um Buchhaltung). Schließlich ist fast die Hälfte der gefälschten Dissertationen speziell auf die Wirtschaft ausgerichtet, weshalb es nicht so schwierig ist, vernünftig über wirtschaftliche Themen zu streiten. Wir werden auch auf diesem Gebiet unsere Stärke versuchen, gut, nirgendwo ist die Ungerechtigkeit dieser Welt akuter als in der Frage der Verteilung des Reichtums. Unabhängig davon, was ein Mensch tut, egal welchen Beruf er besitzt, ist er in die Wirtschaft und ihre Spiele involviert, sowohl nach den Gesetzen der Wirtschaft als auch nach den Gesetzen der Physik, um sich nicht zu verstecken.
Von der ganzen Masse der Probleme, die durch die mathematische Ökonomie gelöst werden, werden wir nur eines betrachten - wie sich herausstellt, dass selbst unter gleichen Bedingungen für alle Marktteilnehmer und einem fairen Geldwechsel die Armen reicher werden als die Reichen und warum selbst eine ideale mathematische Gesellschaft zu finanzieller Ungleichheit neigt. Unterwegs lernen wir etwas Interessantes über mathematische Statistiken und Verteilungen von Zufallsvariablen.
Ich bin ein Physiker durch Ausbildung und Beruf, und meine berufliche Verformung drückt sich in einer besonderen Sicht der Welt aus, wie in einer Vielzahl verschiedener physikalischer Systeme und Prozesse. Aus Sicht eines Physikers ist der reale Markt ein im Wesentlichen instationäres offenes System mit vielen Freiheitsgraden, in dem stochastische (zufällige) Prozesse eine wichtige Rolle spielen. In diesem Sinne ähnelt der Markt dem Thema der Untersuchung von Bereichen der Physik wie Thermodynamik und statistischer Physik, in denen angesichts der Unmöglichkeit, alle unzähligen Details und das Verhalten aller Komponenten des Systems zu berücksichtigen, auf generalisierende und messbare Eigenschaften wie Energie, Temperatur oder Druck umgeschaltet wird . Es ist nicht überraschend, dass seit mehr als hundert Jahren Versuche unternommen werden, Wirtschaftssysteme thermodynamisch zu beschreiben und Wirtschaftsphysik zu schaffen. Das Problem ist jedoch: Während Wissenschaftler die Details betrachten, das gewonnene Wissen zusammenfassen und über grundlegende Gesetze streiten, ist das Hauptziel des Studiums die wirtschaftliche Realität und hat Zeit, sich bis zur Unkenntlichkeit zu ändern. Ihr Verhalten scheint zu versuchen, seine Unsicherheit und Unvorhersehbarkeit zu bewahren oder sogar zu erhöhen.
Ein gutes Beispiel ist die zweihundertjährige Geschichte der Verwendung technischer Analysen beim Spielen an der Börse. Wenn ein neues leistungsstarkes Tool angezeigt wird, mit dem Sie nach versteckten Mustern suchen und den Preis eines Wertpapiers oder einer Aktie vorhersagen können, wird für diejenigen, die es verwenden, ein Gewinn erzielt. Aber bald beginnt der Markt, neue Spieler zu „fühlen“ und sich an ihre Strategie anzupassen, die Genauigkeit der Vorhersagen der wunderbaren Methode beginnt zu sinken und nach einiger Zeit fällt er in eine große Liste veralteter und nicht sehr zuverlässiger Tools. Weder moderne flexible selbstlernende neuronale Netzwerkalgorithmen noch superschnelle Roboterhändler, die Millionen von Operationen pro Minute ausführen, haben in den letzten zwei Jahrzehnten die Haupteigenschaft des Börsenspiels verändert - seine Unvorhersehbarkeit. Und bis jetzt sind die Hauptvorteile eines Profis in dieser Branche Wille, Ausdauer des Charakters, Abneigung gegen Leidenschaft ... nun ja oder Besitz des Austauschs. Alles ist wie in einem Casino, in dem Spiele auf reinem Zufall basieren! Einerseits ist dies natürlich beleidigend und andererseits bietet es Gelegenheit, Methoden und Ansätze ständig zu verbessern. Es war einmal, dass sowohl die Wahrscheinlichkeitstheorie als auch die mathematische Statistik aus Versuchen entstanden waren, Glücksspiele und Wirtschaftsspiele zu analysieren, und erst dann fanden sie Anwendung in fast allen Naturwissenschaften.
In der weiteren Diskussion werden wir über Geld sprechen, aber diese bekannte alltägliche Kategorie ist überraschend komplex und mehrdeutig. Die Bedeutung und der Wert von Geld hängen von vielen Faktoren ab, und aus dem Zusammenhang heraus, wenn wir einen bestimmten Geldbetrag nennen, sagen wir nichts über seinen tatsächlichen Wert aus. Dies unterscheidet Geldwerte von den meisten physischen Größen, die unsere Welt beschreiben, und erschwert es, strenge Diskussionen in der Wirtschaft zu führen. Aber der Zweck unseres Gesprächs: die mathematischen Grundlagen der Gesetze der Gemeinheit, alltäglich, verständlich und einfach. Daher werden wir in Zukunft über einige "Rubel" sprechen, die sich auf ein formelles Ticket oder eine Münze beziehen, und implizieren, dass diese Leute umso reicher sind, je mehr sie "Rubel" haben. Andere Diskussionen über Kaufkraft, immaterielle oder illiquide Werte, über „Geld ist kein Glück“ werden wir schließlich aus dem Gespräch herauslassen.
Komm schon, hör auf!
Wir beginnen mit der Analyse der Gerechtigkeit einiger einfacher Strategien zur Verteilung eines bestimmten Geldbetrags an eine endliche Gruppe von Menschen.
Die erste, naheliegendste Strategie: „Nimm alles und teile es“, dh jedem Mitglied der Gruppe einen gleichen Anteil am Gesamtbetrag zu geben. Eine solche Verteilung wird als
entartet bezeichnet , hat einen Gini-Index gleich Null und entspricht einer Gleichheitskurve im Lorentz-Diagramm.
Absolut faire entartete Geldverteilung: Jeder ist gleich geteilt.Tolle Option! Wir werden es
"Sharikovs Strategie" zu Ehren des Helden des Romans von Michail Bulgakow "Hundeherz" nennen, der auf diese Weise vorschlug, alle wirtschaftlichen Probleme zu lösen.
Die zweite, realistischere Strategie besteht darin, einen Rubel nach dem Zufallsprinzip an alle zu verteilen. Wer hat Glück. Wir können diese Strategie
„Poisson“ nennen , da auf diese Weise unabhängige zufällige Ereignisse im Poisson-Prozess auf der Zeitskala verteilt werden. Für eine Gruppe von
n Person ist die Wahrscheinlichkeit, dass jeder der Teilnehmer den Rubel erhält
1 / n . Nach der Verteilung auf diese Weise
M. Rubel sollte jeder einen Betrag erhalten, der der Anzahl solcher "positiven" Ergebnisse entspricht. Die Wahrscheinlichkeitsfunktion für eine solche Summe ist bekannt - es handelt sich um eine
Binomialverteilung , ähnlich einer Glocke, die symmetrisch um den Durchschnittswert verstreut ist
M / n . Normalerweise stellen sie ihn ihm vor, indem sie die Wahrscheinlichkeit berechnen, den angegebenen Betrag durch Würfeln zu erhalten. Für große Werte
M. Die Binomialverteilung ist von der Normalverteilung kaum mehr zu unterscheiden. Mal sehen, wie es sich ändern wird, wenn das Geld verteilt wird, die Verteilung des Geldes in der Gruppe und seine Fairness.
Das Ergebnis der Geldverteilung nach dem Prinzip "Wen Gott senden wird" ist eine Binomialverteilung. Je mehr Geld wir ausgeben, desto größer ist der Wert des Durchschnitts und des Spread, aber die Wahrscheinlichkeit, nichts zu bekommen, verschwindet fast.Poisson-StrategiealgorithmusAnfangsdaten : xs - ein Array von n Elementen, die mit Nullen gefüllt sind, M - der Gesamtgeldbetrag im System.
M i <- 1 n xs[i] <- xs[i] + 1
Diese Verteilung sieht aus Sicht der Gerechtigkeit sehr gut aus. Außerdem wird sie umso fairer, je mehr Geld wir der Öffentlichkeit geben! Einfach toll! Es ist schade, dass die Gesellschaft nicht auf die gleiche Weise organisiert ist und dass der Regen nicht gleichermaßen aus dem Geld auf uns alle fließt.
Um das Bild zu vervollständigen, schauen wir uns eine andere einfache künstliche Verteilung von Geld an -
Uniform . Mit dieser Verteilung werden die Armen genauso sein wie die Reichen.
Eine gleichmäßige Verteilung bedeutet nicht, dass das Geld gleichmäßig über alle verteilt wird. Bei dieser Verteilung ist die Anzahl der reichen, armen und mittleren Bauern gleich, aber das Geld gehört hauptsächlich den Reichen.Algorithmus für eine gleichmäßige VerteilungsstrategieAnfangsdaten : xs - ein Array von n Elementen, die mit Nullen gefüllt sind, M - der Gesamtgeldbetrag im System.
x xs x <- 0 M/n
Für eine gleichmäßige Verteilung ist die Lorentz-Kurve eine quadratische Parabel, und wenn die linke Grenze der Verteilung Null ist, ist diese Parabel unabhängig von der Position der rechten Grenze, und der Gini-Index für alle derartigen Verteilungen ist genau
1 / 3 . Ein solcher Indexwert (aber keine solche Verteilung!) War zum Beispiel in der australischen Wirtschaft in den 2000er Jahren - dies ist ein ziemlich guter Indikator.
Der Markt ist jedoch der Markt! Die oben betrachteten Verteilungen sind gut, erfordern jedoch besondere Bedingungen für ihr Auftreten. Wenn Sie den Menschen die Freiheit geben, Geld auszutauschen, Geld für Dienstleistungen zu wechseln, es zu speichern und in einer Nacht auszugeben, verlieren ideale Verteilungen an Stabilität und verwandeln sich in andere.
Neue Wirtschaftspolitik!
Betrachten Sie eine Gruppe von
n die Person. Als Ergebnis der Revolution werden wir an alle Teilnehmer des Experiments den gleichen Geldbetrag verteilen - für
m Rubel an alle, die die fairste Sharikov-Verteilung der Gelder in der Gesellschaft erhalten haben. Jetzt geben wir ihnen die Freiheit, durch den Willen ihres eigenen Schicksals reich und verarmt zu werden und ein primitives Marktmodell aufzubauen. Wir bitten jemanden, der zufällig ausgewählt wurde, einer Person in der Gruppe, die ebenfalls zufällig ausgewählt wurde, einen Rubel zu geben. Angenommen, dies ist der Kauf einer bestimmten Dienstleistung zu einem festen Preis. Die Verteilung des Reichtums wird sich voraussichtlich ändern: Jemand wird weniger Geld haben, jemand mehr. Lassen Sie uns den Austauschvorgang immer wieder wiederholen und untersuchen, wie sich die Verteilung des Wohlstands in der Gruppe ändern wird.
Es ist ratsam, vor der Durchführung des Experiments darüber nachzudenken, was wir erwarten. Der Geldaustausch zwischen den Teilnehmern erfolgt ebenso wahrscheinlich wie bei der Poisson-Strategie der Geldverteilung, gleichzeitig verlieren die Spieler jedoch nach dem gleichen Poisson-Prinzip und mit der gleichen Intensität Geld. Somit kann angenommen werden, dass sowohl positive als auch negative Inkremente normalverteilt sind und symmetrisch in Bezug auf Null angeordnet sind. Jeder Spieler erhält letztendlich eine Differenz dieser Inkremente, die für zwei normalverteilte Zufallsvariablen ebenfalls normalverteilt sind, in diesem Fall um Null, da Verluste und Gewinne symmetrisch sind.
Nach vielen Umtauschaktionen erhält und verliert jeder Spieler einen Betrag, der einer nahezu normalen Verteilung entspricht. Der Gesamtumsatz wird normalerweise auch um Null verteilt.Somit erhalten wir einen klassischen Random Walk mit normalverteilten Inkrementen und können eine gewisse Diffusion der Mittel um den Mittelwert erwarten
m . Die Wahrscheinlichkeitsfunktion sollte unscharf sein und die Varianz bei einem konstanten Durchschnittswert erhöhen. Alles scheint einfach zu sein.
Aber es gibt eine Nuance. Wenn jemand aus der Gruppe aus irgendeinem Grund kein Geld mehr hat, kann er keine Dienstleistungen kaufen, indem er Geld gibt, aber gleichzeitig kann er es erhalten. Der mögliche Wert des Vermögens ist links auf Null begrenzt, was bedeutet, dass sich die Verbreitung des Vermögens nicht unbegrenzt ausbreiten kann und die beobachtete Wahrscheinlichkeitsfunktion früher oder später nicht mehr symmetrisch ist.
Es gibt noch eine Nuance. Der Geldbetrag in unserem geschlossenen System ist begrenzt und unveränderlich, was bedeutet, dass zufällige Spaziergänge nicht unabhängig sind. Einige glückliche Spieler werden in der Lage sein, sehr große Mengen zu erhalten und sich sehr weit vom Ensemble zu entfernen, aber nur, wenn die Gesamtmasse ärmer wird. Die Teilnehmer des Experiments werden durch das Gesetz, Geld im System zu sparen, durch ein unsichtbares Netzwerk zusammengezogen. Was wird die Geldverteilung unter solchen Bedingungen anstreben? Es scheint, dass die Antwort nicht so offensichtlich ist, wie es auf den ersten Blick erscheinen mag. Wenden wir uns der Simulation zu und sehen, was passiert.
Simulationsergebnis für das Teilen eines gleichen Geldbetrags für n = 1000 und m = 100 . Zunächst wird zwar ein diffusionsähnliches Phänomen beobachtet, aber wenn die Wahrscheinlichkeitsfunktion die linke Grenze erreicht, tendiert die Verteilung zu einer charakteristischen asymmetrischen und nicht sehr fairen Form mit einem Gini-Koeffizienten nahe 0,5 .Algorithmus für gleiche MengenAnfangsdaten : xs - ein Array von n Elementen, das mit m Werten initialisiert wurde.
i <- 0 n xs[i] > 0 j <- 0 n xs[i] <- xs[i] - 1 xs[j] <- xs[j] + 1
Wenn ein Physiker dieses Buch liest, kann er zuversichtlich annehmen, dass dies eine Verteilung sein könnte, und er wird es die Gibbs-Verteilung nennen. Ein aufmerksamer Leser kann sich daran erinnern, dass wir bereits auf ein ähnliches Bild und einen solchen Gini-Index gestoßen sind, als wir die Frustration beim Warten auf einen Bus untersuchten. Dann untersuchten wir die Verteilung der Intervalle zwischen Poisson-Ereignissen, die durch eine Exponentialverteilung beschrieben wurde. Diese beiden klugen Herren werden Recht haben und verschiedene Namen die gleiche wunderbare Verteilung nennen.
Menschen sind Moleküle
Die Gibbs-Verteilung stammt aus dem Bereich der statistischen Physik. Es beschreibt die Eigenschaften von Systemen, die als das schöne Wort "Ensemble" bezeichnet werden und aus sehr vielen interagierenden Elementen bestehen, meistens Partikeln. Im Ensemble können Sie beliebige Subsysteme (z. B. einzelne Partikel oder deren Gruppen) auswählen und ihnen bestimmte Zustandsfunktionen zuweisen (dies können verallgemeinerte Koordinaten, Geschwindigkeiten, Konzentrationen, chemische Potentiale und vieles mehr sein). Mit den Methoden der statistischen Physik können die Parameter einer Vielzahl von Phänomenen erklärt und berechnet werden: chemische und katalytische Prozesse, Turbulenzen, Ferromagnetismus, Verhalten von Flüssigkristallen, Superfluidität und Supraleitung und viele andere.
Die Gibbs-Verteilung beantwortet die Frage: Wie hoch ist die Wahrscheinlichkeit, einen bestimmten Zustand des Teilsystems zu erreichen, wenn a) die Zustandsenergie angegeben wird, b) die makroskopischen (relativ gesehen globalen) Eigenschaften des Systems wie die Temperatur und c) ist bekannt, dass sich das System im thermodynamischen Gleichgewicht befindet? Es kann schematisch wie folgt ausgedrückt werden:
p m a t h r m G i b b s ( T ) ( x ) = C e - f r a c E ( x ) k T ,
wo
x - einen bestimmten Zustand des Teilsystems,
E ( x ) Ist die Energie dieses Zustands,
T. Ist die absolute Temperatur des Systems (oder seines Analogons) und
C. und
k - Werte, die für die Normalisierung und Übereinstimmung der Abmessungen erforderlich sind. Die Gleichgewichtsbedingung ist sehr wichtig, dies bedeutet, dass die Zeit aus der Betrachtung verschwindet und das gesamte System unter den gegebenen Bedingungen in seinem wahrscheinlichsten Zustand ist.
Wir brauchen hier keine rigorose Ableitung des Ausdrucks für die Gibbs-Verteilung, sondern ich möchte eine schöne rein mathematische Argumentation zeigen, die zu ihrer Exponentialform führt. Da wir die Teile des Systems betrachten, die sich zum gesamten System addieren, lohnt es sich, eine
additive Größe als ihre Eigenschaft zu wählen,
dh , dass ihr Wert für das Ensemble die arithmetische Summe der Werte seiner Teile ist. Energie kann als solche Größe in der Mechanik verwendet werden. Andererseits berechnen wir die Wahrscheinlichkeit, einen bestimmten Zustand des Systems zu beobachten, und die Wahrscheinlichkeit ist
multiplikativ , dh wenn das System in Teile unterteilt werden kann, ist die Wahrscheinlichkeit, alle diese Teile gleichzeitig zu beobachten, gleich dem Produkt der Wahrscheinlichkeiten für den Zustand jedes Teils. Wir brauchen also eine Funktion, die eine additive Größe in eine multiplikative verwandelt. Nur die Exponentialfunktion hat diese Eigenschaft.
a x Die Summe der Argumente wird zu einem Produkt von Werten:
a x + y = a x a y . Nun, von allen Exponentialfunktionen ist der Exponent am bequemsten, da er sich bei Integration und Differenzierung sehr gut verhält.
In unserem Marktmodell haben wir eine additive Menge - die Menge an Geld, die jeder Spieler hat, dies ist ein Analogon der Energie. Bei dem von uns beschriebenen Austausch bleibt diese Menge ebenso wie die Energie im physikalischen System erhalten. Und wo ist die Temperatur? Es ist leicht herauszufinden, indem man den Ausdruck für die Wahrscheinlichkeitsdichte der Exponentialverteilung betrachtet:
p mathrmExp( lambda)(x)= lambdae− lambdax,
und daran erinnern, dass der Durchschnitt für ihn ist
1/ lambda . Da die Anzahl der Spieler während des Gebotsverfahrens unverändert bleibt, entspricht der arithmetische Durchschnittsbetrag der Spieler dem ursprünglich verteilten Betrag
m . Daraus folgt natürlich das
lambda=1/m Dann wirkt der durchschnittliche Geldbetrag der Spieler als Temperatur in unserem Wirtschaftsmodell. In einem „aufgewärmten“ Markt mit großer Liquidität können wir eine größere Streuung des Wohlbefindens beobachten als in einem „kalten“, da die Streuung in der Exponentialverteilung gleich ist
1/ lambda2 . Wie Ostap Bender im „Goldenen Kalb“ von I. Ilf und E. Petrov sagte: „Wenn einige Banknoten im Land herumlaufen, muss es Menschen geben, die viele davon haben.“
Um genau zu sein und daran zu erinnern, dass Geld in unserem Experiment eine diskrete Größe ist, beobachten wir eine
geometrische Verteilung - ein diskretes Analogon der Exponentialverteilung. Es tritt das Problem auf, die Anzahl der Fehler vor dem ersten Gewinn zu zählen, wenn Münzen mit unterschiedlichem Ehrlichkeitsgrad geworfen werden. Diese beiden Verteilungen sind ähnlich und werden mit abnehmender Gewinnwahrscheinlichkeit nicht mehr zu unterscheiden. In unserem Experiment sind die Chancen, den Rubel zu bekommen, gleich
1/1000 ist es klein genug, um die Verteilung exponentiell zu nennen.
Es bleibt das Gleichgewicht des Endzustands des Marktes zu behandeln. Das thermodynamische Gleichgewicht kann auf verschiedene Arten beschrieben werden. Erstens sollte sich der
stationäre Zustand im
Gleichgewicht befinden , in dem das System unbegrenzt bleiben kann, ohne seine makroskopischen Parameter zu ändern und ohne geordnete Flüsse von Materie und Energie in sich selbst zu bilden. Zweitens muss es
stabil sein , dh wenn das System nicht ausbalanciert ist, kehrt es tendenziell dorthin zurück. Drittens ist dies der wahrscheinlichste Zustand des Systems, der am häufigsten beobachtet wird und in den das System im Laufe der Zeit dazu neigt, aus einem anderen Nichtgleichgewichtszustand zu gelangen. Unser Experiment zeigt diese Kriterien für das Gleichgewicht: Nachdem das System zu einer Exponentialverteilung gelangt ist, bleibt es darin, und außerdem kann im Experiment leicht sichergestellt werden, dass wir nach einiger Zeit aus einer beliebigen Verteilung wieder zu einer Exponentialverteilung gelangen. Dies ist jedoch kein Beweis, sondern nur ein Hinweis darauf, dass es sich höchstwahrscheinlich um ein Gleichgewicht handelt. Wir brauchen eine Art formal messbares Kriterium, das uns eindeutig anzeigt, dass das System im Gleichgewicht ist, ohne auf unbestimmte Zeit warten oder alle möglichen Anfangsverteilungen sortieren zu müssen. Dies wäre ein nützliches Kriterium, das auf den realen Markt angewendet werden könnte, ohne dass riskante Experimente an lebenden Menschen durchgeführt werden müssten.
Tao in Worten ausgedrückt - nicht wahres Tao
Reflexionen über das Gleichgewicht führten die Physiker zu dem Konzept der
Entropie , das allmählich über die Thermodynamik hinausging und von Wissenschaftlern aller Richtungen, Philosophen und der Öffentlichkeit so beliebt war, dass die Entropie nun eine Aura des Geheimnisses, der Unverständlichkeit erhalten hat und Gott etwas anderes weiß. Ein einfaches und spezielles Konzept erlangte im Wesentlichen in den Köpfen der Massen einen Ruf als unerklärlich regierendes Konzept der Welt. Dies liegt an der Tatsache, dass die Thermodynamik eine universelle Wissenschaft ist, die auf einer sehr hohen Abstraktionsebene ein System sehr unterschiedlicher Natur beschreibt: von physikalisch, chemisch und biologisch bis sozial, wirtschaftlich und sogar rein humanitär. Nach dem Schulkurs bleibt jedoch das Gefühl, dass es bei der Thermodynamik um ein langweiliges ideales Gas, einige Kolben und einen unmöglichen Carnot-Zyklus geht. Eine solche sehr einseitige Sichtweise hängt mit der bemerkenswerten Tatsache zusammen, dass die Thermodynamik als einer der abstraktesten und universellsten Zweige der Naturwissenschaften angewandte Probleme elegant löst, die für Schulkinder verständlich und in der Industrie nützlich sind. Dies kann zum Beispiel nicht über Kategorietheorie oder Topologie gesagt werden, die ebenfalls sehr abstrakte, universelle und zweifellos nützliche Disziplinen sind, aber sie werden bei alltäglichen Aufgaben fast nie angetroffen.
Also Entropie. Der Schöpfer der Thermodynamik, Clausius und später Gibbs und Boltzmann, benötigten eine quantitative Eigenschaft des Gleichgewichts, die die Wahrscheinlichkeit angibt, den angegebenen Zustand des Systems oder seiner Teile zu beobachten. Darüber hinaus muss dieser Wert, der eine multiplikative Wahrscheinlichkeit widerspiegelt, eine additive Zustandsfunktion sein, damit er für das System berechnet werden kann, indem die für seine Teile berechneten Werte addiert werden. Als wir nach einer geeigneten Funktion für die Gibbs-Verteilung suchten, gingen wir davon aus, dass ein additives Argument in einen multiplikativen Wert umgewandelt werden sollte. Bei der Suche nach einem Ausdruck für Entropie benötigen wir eine Funktion, deren Argument multiplikativ und deren Wert additiv ist - dies ist eine logarithmische Funktion, die Umkehrung des Exponentials. Die Entropie des Zustands eines komplexen Systems kann ausgedrückt werden als der erwartete Wert für den Logarithmus der Wahrscheinlichkeit, den Zustand aller seiner Teile zu beobachten, oder nach Boltzmann als der Logarithmus der Anzahl von Möglichkeiten, wie dieser Zustand des Systems realisiert werden kann. In diesem Fall entspricht der wahrscheinlichere Zustand einem größeren Entropiewert und dem Gleichgewichtszustand dem maximal möglichen.
Die Anzahl der Möglichkeiten, diesen oder jenen Zustand zu realisieren, hängt von der Anzahl der Einschränkungen oder Bedingungen ab, unter denen dieser Zustand realisiert werden kann. Je weniger solche Einschränkungen bestehen, desto wahrscheinlicher ist der Staat und desto größer ist der Wert seiner Entropie. Diese Einschränkungen und Bedingungen sind für Statusinformationen sinnvoll. Daher die Idee, dass Entropie den Grad unserer Unkenntnis des Systems widerspiegelt: Je weniger wir über den Staat wissen, desto größer ist seine Entropie. Shannon verallgemeinerte dieses Konzept später für alle Systeme, die Informationen enthalten, einschließlich für die Verteilung von Zufallsvariablen. Folgendes hat er getan: für eine Zufallsvariable
X definiert durch eine Wahrscheinlichkeitsfunktion
p(x) Entropie ist wie folgt definiert:
H(X) äquiv− mathrmM( ln(p(x)))=− sump(x) ln(p(x)),
Dabei wird die Summierung über alle Werte durchgeführt
x in dem
p(x)>0 . Auf diese Weise können wir die Entropie des Zustands jedes komplexen Systems anhand seiner statistischen Beschreibung berechnen.
So ändert sich die Entropie, wenn unser Marktmodell ins Gleichgewicht kommt.
Das Wachstum der Entropie, wenn sich der Markt dem Gleichgewichtszustand nähert. Die horizontale Linie im rechten Diagramm zeigt den theoretischen Entropiewert für die Exponentialverteilung gleich 1− ln( lambda) . Das Zwischen- „Regal“ entspricht dem Zeitraum, in dem die Verteilung die Diffusionsphase durchlief und wie normal aussah.Somit kann jede Verteilung, die analytisch definiert oder experimentell in Form eines Histogramms erhalten wird, einer positiven Zahl zugeordnet werden - ihrer Entropie. Dies bedeutet, dass Verteilungen miteinander verglichen werden können, um mehr oder weniger Gleichgewicht zu bestimmen und für gegebene Bedingungen wahrscheinlich zu sein. Darüber hinaus ist es für eine bestimmte Verteilungsklasse möglich, eine Verteilung mit maximaler Entropie zu unterscheiden, außerdem nur eine. Klassen werden durch Einschränkungen oder das Maß unseres Wissens über die statistischen Eigenschaften eines Systems definiert. Hier einige Beispiele:
| Was wissen wir über die Zufallsvariable? X | Verteilungen mit maximaler Entropie |
|---|
| X i n [ a , b ] | gleichmäßig über den Schnitt [ a , b ] |
| X \ in \ {0,1 \} | Bernoulli-Vertrieb |
| X in[0, infty) + Durchschnitt | exponentiell für eine diskrete Größe - geometrisch |
| X in[xm, infty) + geometrisches Mittel | Pareto-Verteilung (Macht) |
| X in[0, infty) + Durchschnitt + geometrisches Mittel | Gammaverteilung |
| X in[0, infty) + geometrisches Mittel + Varianz für geometrisches Mittel | log normal |
| X in(− infty, infty) + Durchschnitt + Varianz | normal |
Vertraute alle Gesichter! Dies sind sehr häufig verwendete Verteilungen, die Statistiker auf die breiteste Klasse von Aufgaben anwenden. Ihre Universalität beruht genau auf der Tatsache, dass sie bei maximaler Entropie am wahrscheinlichsten und beobachtbarsten sind. Zu ihnen neigen als Gleichgewicht viele Verteilungen von realen Zufallsvariablen. Unter allen anderen ist die Normalverteilung am freiesten von Einschränkungen: Sie erfordert ein Minimum an Informationen über eine Zufallsvariable. Weniger wird scheitern: Wenn wir nur den Durchschnittswert angeben, wird die Verteilung in dem Bestreben, die Entropie zu erhöhen, entlang der gesamten numerischen Achse „verschmiert“.
Wenn wir jedoch nur den Durchschnittswert kennen und gleichzeitig die Zufallsvariable auf positive Werte beschränken, ist die Gleichgewichtsverteilung eindeutig - exponentiell. Diesen Fall haben wir in unserem Experiment mit dem Markt beobachtet. Wir wussten im Voraus nur, wie viel Geld wir an jeden Spieler ausgegeben haben und dass der Geldbetrag im System konstant war, was einen Durchschnittswert festlegte. Und da unser Geld höchstwahrscheinlich im Gleichgewicht positiv ist, erhalten wir die exponentielle Verteilung des Wohlstands mit dem Gini-Index gleich1/2 .
Es gibt viele Modifikationen des von uns beschriebenen Modells: Der Austausch kann nicht in einem Rubel stattfinden, sondern in einem zufälligen Wert, der durch den Zustand des Gebers begrenzt ist, während es möglich ist, Geld keinem Spieler zu geben, sondern es zufällig zu verteilen. Bis wir neue Parameter in das Spiel einführen, ändern all diese Modifikationen nicht die Form der Gleichgewichtsverteilung des Reichtums - sie bleibt exponentiell. Sie können dies mithilfe der Simulation überprüfen. Es ist jedoch nicht interessant, Bilder für verschiedene Austauschmethoden bereitzustellen - sie sind alle gleich. Viele Forscher haben dieses Merkmal von Marktmodellen festgestellt. Ein interessantes Modell ist das von Dragulescu und Yakovenko von der University of Maryland erstellte Modell, bei dem Spieler zu bestimmten Unternehmen zusammengefasst werden und anschließend die Interaktion der Unternehmen mit den Spielern, Arbeitern und Käufern simuliert wird.Aber auch in diesem komplexen Fall ist das Gleichgewicht die Exponentialverteilung, die den gewählten Parametern des Modells gleichgültig ist.Um die Universalität des Prinzips der maximalen Entropie zu demonstrieren, lassen Sie uns das Vermögen eines einzelnen Spielers von oben künstlich einschränken und ihm verbieten, Geld zu erhalten, wenn er bereits einen festen Betrag hat. Die Gleichgewichtsverteilung wird sich natürlich ändern. Und wenn der rechte Rand dem doppelten Durchschnittswert entspricht, kommen wir zu dem in der ersten Zeile der Tabelle beschriebenen Fall. Wenn wir die Zufallsvariable auf ein endliches Segment beschränken und nichts anderes angeben, können wir keinen anderen erwarteten Wert des Durchschnitts annehmen, außer der Mitte dieses Segments. Daher sollte die Gleichgewichtsverteilung mit dieser Option gleichmäßig sein. Lassen Sie uns überprüfen, ob dies so ist.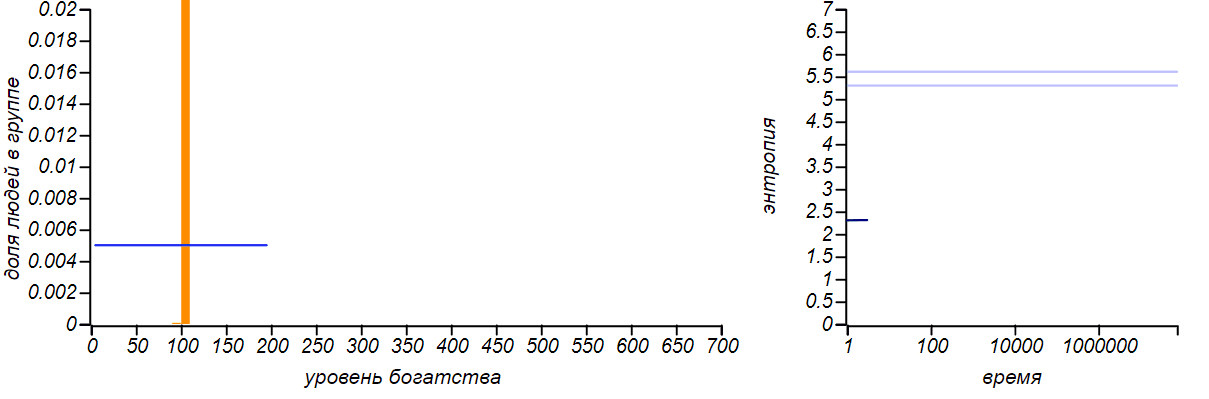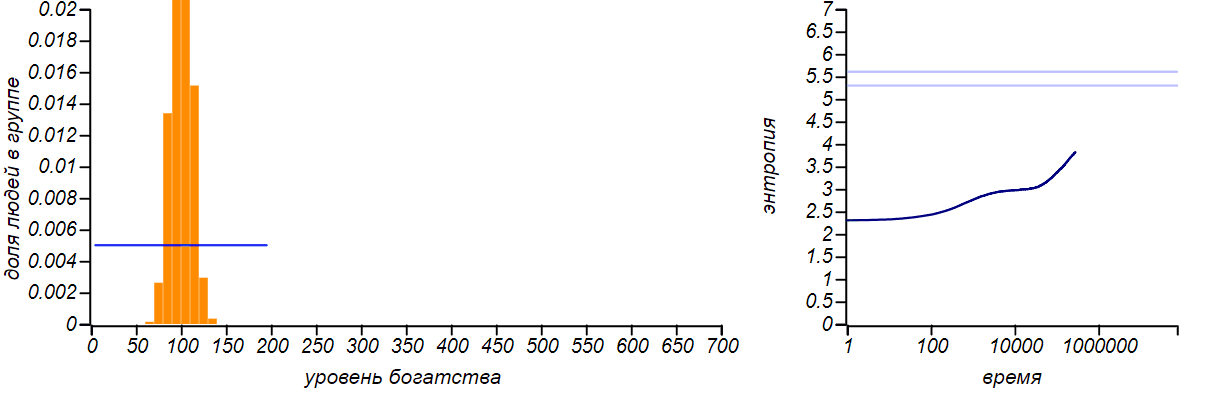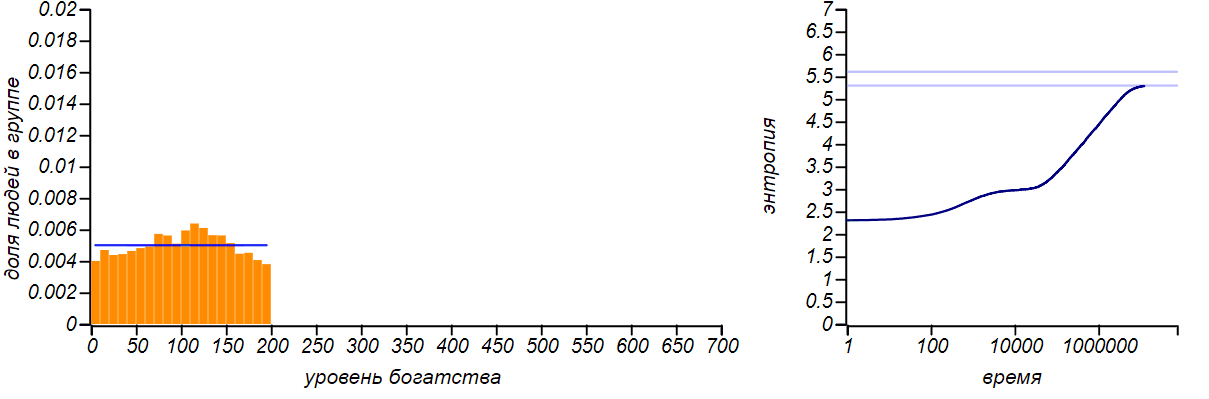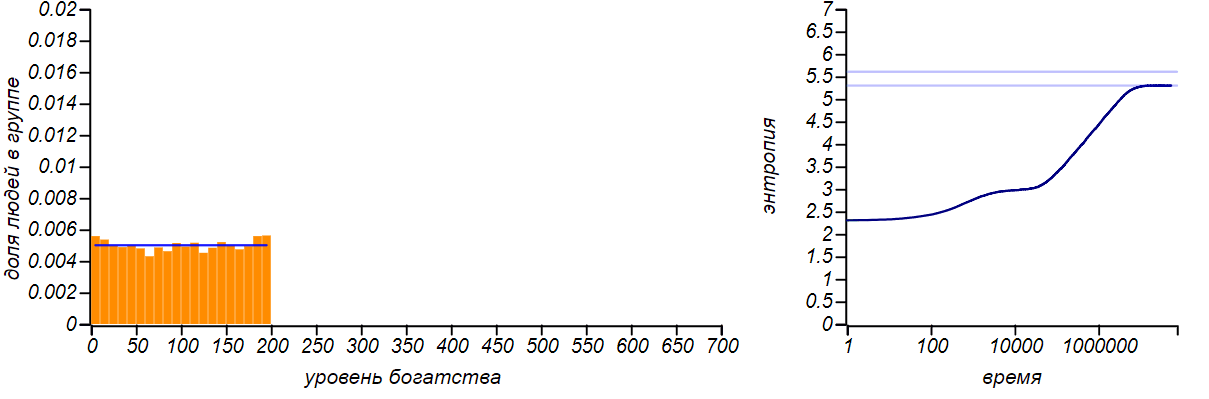
Algorithmus zum Austausch gleicher Beträge mit einer Einschränkung an der Spitze: xs — n , m , xMax — .
i <- 0 n xs[i] > 0 j <- 0 n xs[j] < xMax xs[i] <- xs[i] - 1 xs[j] <- xs[j] + 1
Und was passiert, wenn die Symmetrie gebrochen ist, dh wenn wir den rechten Rand nach rechts oder links verschieben?<\ br>Varianten asymmetrisch begrenzter Verteilungen im Vergleich zu Bernoulli-Verteilungen entsprechend der Verschiebung des Durchschnittswertes. Die horizontalen Linien in den Entropiediagrammen geben die theoretischen Werte für die Entropie der Bernoulli-Verteilungen an.Die Verteilung des Reichtums war nicht mehr einheitlich und nahm die Form eines begrenzten Exponentials an. Mit der Verschiebung der rechten Grenze nach links wurde das Gleichgewicht der reichen Spieler mehr als arm. Wenn wir das Histogramm mit nur noch zwei Spalten „aufrauen“, erhalten wir die Bernoulli-Verteilung, die zeigt, wie wahrscheinlich es ist, dass es bedingt „arm“ oder „reich“ ist. Wenn die Werte einer Zufallsvariablen auf nur zwei Werte beschränkt sind, ist die Bernoulli-Verteilung die einzige Wahl, die natürlich ein Maximum an Entropie liefert. Beachten Sie jedoch, dass die Entropie unserer Modellverteilungen genau den von der Bernoulli-Verteilung vorhergesagten Werten entspricht. Die Gini-Koeffizienten für diese beiden Fälle sind gleich0.43 und
0.2 jeweils.Eine mysteriöse und mächtige Entropie ist natürlich cool und vielleicht sogar überzeugend. Aber warum werden die Armen bei einem symmetrischen Austausch reicher als die Reichen? Warum ist der Gleichgewichtsverteilungsmodus gleich Null? Wie Physiker sagen, ist es notwendig, die Kinetik des Prozesses zu verstehen, dh das Schicksal einzelner Teilchen. Wir haben uns nicht geirrt anzunehmen, dass das Random-Walk-Modell eine Änderung des Zustands eines einzelnen Bieters beschreibt: Es ist gleich wahrscheinlich, dass er Schritte nach oben und unten unternimmt. Und für einen zufälligen Spaziergang ist ein berühmtes Gesetz der Gemeinheit erfüllt: der Fluch des Spielers. Ich möchte Sie daran erinnern, dass es darin besteht, dass sich bei einer ausreichend langen Beobachtung ein zufällig wanderndes Teilchen notwendigerweise an jeder im Voraus angegebenen Stelle befindet.Darüber hinaus ist die Entfernung, in der sich das Partikel von einem Startpunkt entfernt, proportional zur Quadratwurzel der Anzahl der Schritte. All dies führt zu der Tatsache, dass ein Teilchen, wenn es seinen Weg in der Nähe von Null beginnt, ihn höchstwahrscheinlich erreicht. Da Null in unserem Problem eine undurchdringliche Grenze ist, wird es gezwungen sein, seinen Weg immer wieder in der Nähe des Nullpunkts zu beginnen und zu erfahren der berüchtigte Fluch. Wenn sich das Teilchen von Null entfernt, nimmt die Wahrscheinlichkeit seiner Rückkehr ab und die Reichen retten mit größerer Wahrscheinlichkeit ihren Zustand. Aber was verhindert dann, dass sich das Teilchen willkürlich weit wegbewegt und ein bestimmter Spieler willkürlich reich wird? In der Tat nichts als die Endlichkeit des Geldes im System - die Exponentialverteilung unterscheidet sich von Null auf der gesamten positiven Achse.Aber um nach den Regeln unseres Spiels unglaublichen Reichtum zu erreichen, ist es notwendig, dass alle Spieler immer wieder zufällig denselben Spieler auswählen. Und zum ersten Mal ist die Wahrscheinlichkeit einer solchen Wahl(1/n)n−1- ein Milliardstel für eine Gruppe von zehn Personen, und es ist zufällig unglaublich, es viele Male zu wiederholen. Die Wahl, wem wir in unserem Modell Geld geben sollen, liegt gleichermaßen bei jedem, was bedeutet, dass er nicht nur reich, sondern auch arm wird. Es gibt Gerechtigkeit auf dieser Welt! Obwohl nicht lange triumphierend, wenn Sie nicht reich sind.Die Wirtschaft muss wirtschaftlich sein
Solange unser Austauschmodell den Wohlstand der Spieler nicht berücksichtigt, bleibt es unrealistisch. Tatsächlich geben die Reichen mehr aus und die Armen weniger, außerdem versuchen vernünftige Leute, einen Teil ihres Vermögens zu erhalten. Als nächste Komplikation des Modells fordern wir, dass die Spieler beim Austausch einen bestimmten bekannten Anteil gebenαsein Zustand. Ein neuer Parameter und eine neue Einschränkung werden in das System eingeführt, daher kann der Gleichgewichtszustand vom exponentiellen abweichen. Unter Verwendung von Bruchteilen des Wohlfahrtsniveaus gehen wir zu multiplikativen Merkmalen über, wie zum Beispiel der Kapitalrendite, der Kapitalrendite usw. In allen Wirtschaftslehrbüchern wird angegeben, dass Sie, wenn Sie beispielsweise über viele Jahre die durchschnittliche Kapitalrendite berechnen möchten, den geometrischen Mittelwert für die Renditen eines jeden Jahres berechnen sollten. In unserem Fall wird das geometrische Mittel eindeutig, wenn auch nicht trivial, durch den Wert bestimmtα .
Durch Hinzufügen eines neuen Parameters legen wir die geometrische Durchschnittsverteilung des Einkommens der Spieler oder die durchschnittliche Rendite des Marktmodells fest. Daher können wir erwarten, dass die Gleichgewichtsverteilung des Wohlstands durch die Gammaverteilung gut beschrieben werden sollte. Wir können davon überzeugt sein, nachdem wir Simulationsmodelle durchgeführt haben.Wenn die Kosten des Austauschs proportional zur Häufigkeit sind, tendiert die Gleichgewichtsverteilung zu einer charakteristischen asymmetrischen glockenförmigen Gammaverteilung. In diesem Modell α=1/3 . Die durchschnittliche Wechselkursrendite betrug 75% .Proportionaler Austauschalgorithmus: xs — n , m , alpha — , .
i <- 0 n xs[i] > 0 dx <- floor(xs[i]*alpha) xs[i] <- xs[i] - dx j <- 0 n xs[j] <- xs[j] + dx
Der Rückgang des Anteils der Armen ist darauf zurückzuführen, dass sie im Durchschnitt weniger ausgeben als sie von den Reichen erhalten, da beide Anteile ihres Kapitals austauschen. Aber dieser soziale Aufzug funktioniert nur, wennα<1/2 .
Wenn Sie mehr als die Hälfte von dem ausgeben, was Sie haben, wird die Wahrscheinlichkeit, in den Armen zu sein, sehr greifbar. Für verschiedene Werteα Sie können in der Formverteilung mit einer Vielzahl von Ungerechtigkeiten sehr unterschiedlich werden:Verschiedene Optionen für Gleichgewichtsverteilungen zu Kosten, die proportional zum Wohlstand sind. Diagramme sind mit Werten markiert α und im rechten Diagramm in Klammern sind auch die Werte des Gini-Index angegeben.Genaue Lösung, , . , , , , , , . , , , .
-
Gamma(k,θ) — , ,
k=1 . , . , — . —
, - , , -. ,
X∼Gamma(k1,θ),Y∼Gamma(k2,θ)⟹X+Y∼Gamma(k1+k2,θ)
, :
X∼Gamma(k,θ)⟹aX∼Gamma(k,aθ).
m α ::
Gamma(1α−1,1m(1α−1)) .
Es ist ersichtlich, dass je mehr Teil der Kapitalakteure gezwungen sind, Geld auszugeben (zum Beispiel für den täglichen Bedarf oder für Lebensmittel), desto größer wird der Anteil der Armen und desto weniger fair wird die Gesellschaft. Neugierig das mitα=1/2Die Gleichgewichtsverteilung wird exponentiell wie im Modell mit gleichem Austausch. Die Exponentialverteilung ist ein Sonderfall der Gammaverteilung, daher ist diese Transformation an sich nicht überraschend. Aber es gibt eine merkwürdige Subtilität: Die Entropie dieses speziellen Falles ist mehr als die Entropie von Verteilungen mit anderen Wertenα .
Sehen Sie, wie sich die Entropie ändert, wenn sich die Situation entwickelt α=0.75 ::
Beim Übergang zum Gleichgewicht „überspringt“ das System den Zustand mit maximaler Entropie.Zuerst steigt der Wert der Entropie monoton an, dann stoppt er und beginnt abzunehmen, ohne ein theoretisches Maximum zu erreichen, das der Exponentialverteilung entspricht. Gibt es einen Widerspruch zur Definition eines Gleichgewichtszustands als Zustand mit maximaler Entropie? Es gibt keinen Widerspruch, da der Gleichgewichtszustand stationär sein muss, dh keine gerichteten Energieflüsse erzeugt und stabil ist oder, wenn man die Sprache der Theorie dynamischer Systeme spricht, ein System an sich zieht. Und von allen stationären Gleichgewichten wird der Zustand mit maximaler Entropie sein. Und in unserem Fallα=0.75entspricht die Exponentialverteilung einem instationären Zustand.Forscher der Boston University Ispolatov und Krapivsky haben das proportionale Austauschmodell so kompliziert, dass der Austausch nicht nur das Wohl der Ausgaben, sondern auch den Empfang berücksichtigt. Ein Millionär kauft selten etwas von einem Gemüsehändler, und ein Gemüsehändler hat selten viel Einkommen. Andererseits wird ein Autohersteller der Extraklasse nur mit wohlhabenden Kunden interagieren, aber er selbst wird nicht unrentabel sein. Und so zerfällt die Gesellschaft in Modellen, in denen die Reichen anfangen, hauptsächlich an die Reichen und die Armen zu zahlen - an die Armen.Wenn Cashflows vom Kapital abhängig werden, verliert das System an Stabilität und führt zu einer ständigen Verarmung der Gruppe und einer Zunahme der Klassenungleichheit. In diesem Beispiel α=0.3,β=0.1 (. ).-: xs — n , m , alpha — , , beta — , .
i <- 0 n xs[i] > 0 dx <- floor(xs[i]*alpha) xs[i] <- xs[i] - dx dx > 0 j <- 0 n d = min(dx, floor(xs[j]*beta)) xs[j] <- xs[j] + d dx <- dx - d
In diesem System gibt es nur einen stationären Zustand: Wenn alle Spieler absolut nichts haben (und daher nicht erhalten) und der gesamte Reichtum an jemanden allein geht. Der Gini-Koeffizient ist in diesem Zustand fast gleich Eins und sehr weit vom normalen Gleichgewicht entfernt - seine Entropie ist fast Null. Die Situation kann durch eine Einschränkung von unten gerettet werden, die es den Spielern verbietet, absolut alle ihre Ersparnisse zu verlieren. In diesem Fall wird die Gleichgewichtsverteilung wieder exponentiell oder gammaförmig. Wir können auch eine Einschränkung von oben einführen - dann erhalten wir eine bestimmte asymmetrische Verteilung, die der Bernoulli-Verteilung entspricht. Das Modell eines solchen wilden Marktes ist ohne Einschränkungen durchaus auf den Wertpapiermarkt anwendbar, aber sie haben an realen Börsen damit zu kämpfen, was zu Einschränkungen des Transaktionsvolumens führt.pro Tag und bei maximalem Wachstum oder Preisverfall eines Vermögenswerts gebunden.All dies sind traurige Schlussfolgerungen, die nicht für den freien Markt sprechen, oder ist es der Fall, das von Sharikov vorgeschlagene Modell! Aber was ist die Entropie einer entarteten Verteilung? Nach der Standardformel ist es genau Null. Dies ist das ungleichste und unwahrscheinlichste Verhältnis, und in jedem Austauschmodell ist es instabil, so dass eine solche Gesellschaft nur künstlich erhalten werden kann. Der wilde Markt ist natürlich kein Geschenk - er ist instabil und neigt zu eklatanter Ungleichheit. Es bedarf vieler einvernehmlicher Beschränkungen und fein abgestimmter Beziehungen, um einen nachhaltigen Markt und eine mehr oder weniger faire Gesellschaft aufzubauen. Die Menschheit hat dieses Thema für eine sehr kurze Zeit und im Grunde genommen durch Berührung, durch Versuch und Irrtum untersucht, aber eines ist klar: Ungerechtigkeit im Wirtschaftsraum ist keine Folge der schmutzigen menschlichen Natur, sondern eine objektive Eigenschaft des Systems.von denen wir alle ein Teil sind. Darüber hinaus gingen Versuche, absolute Gerechtigkeit in einem Sharikov-Stil zu schaffen, immer mit Kampf und Blut einher, und die Ergebnisse existierten aufgrund ihres Ungleichgewichts nicht lange.Es ist unwahrscheinlich, dass Moleküle und Atome über die Ungerechtigkeit ihrer Welt sprechen, und Physiker und Ingenieure haben sich seit zweihundert Jahren damit abgefunden, dass das Chaos unabhängig von der von ihnen gebauten idealen Wärmekraftmaschine nicht zulässt, dass Wärme in mehr als den erforderlichen Anteil umgewandelt wird. Wenn es klar ist, ist es nicht so anstößig. Ich hoffe, dieses Kapitel hilft einem neugierigen Leser, unsere komplexe, ungerechte Welt zu verstehen und zu akzeptieren.