Verteilen Sie die Punkte in Pytorch und Tensorflow gleichmäßig über die Kugel

Dieser Text richtet sich an diejenigen, die an Deep Learning interessiert sind und verschiedene Methoden der Pytorch- und Tensorflow-Bibliotheken verwenden möchten, um die Funktion vieler Variablen zu minimieren. Sie möchten lernen, wie ein sequentiell ausgeführtes Programm in vektorisierte Matrixberechnungen umgewandelt wird, die mit numpy durchgeführt werden. Sie können auch lernen, wie Sie aus Daten, die mit PovRay und Vapory visualisiert wurden, einen Cartoon erstellen.

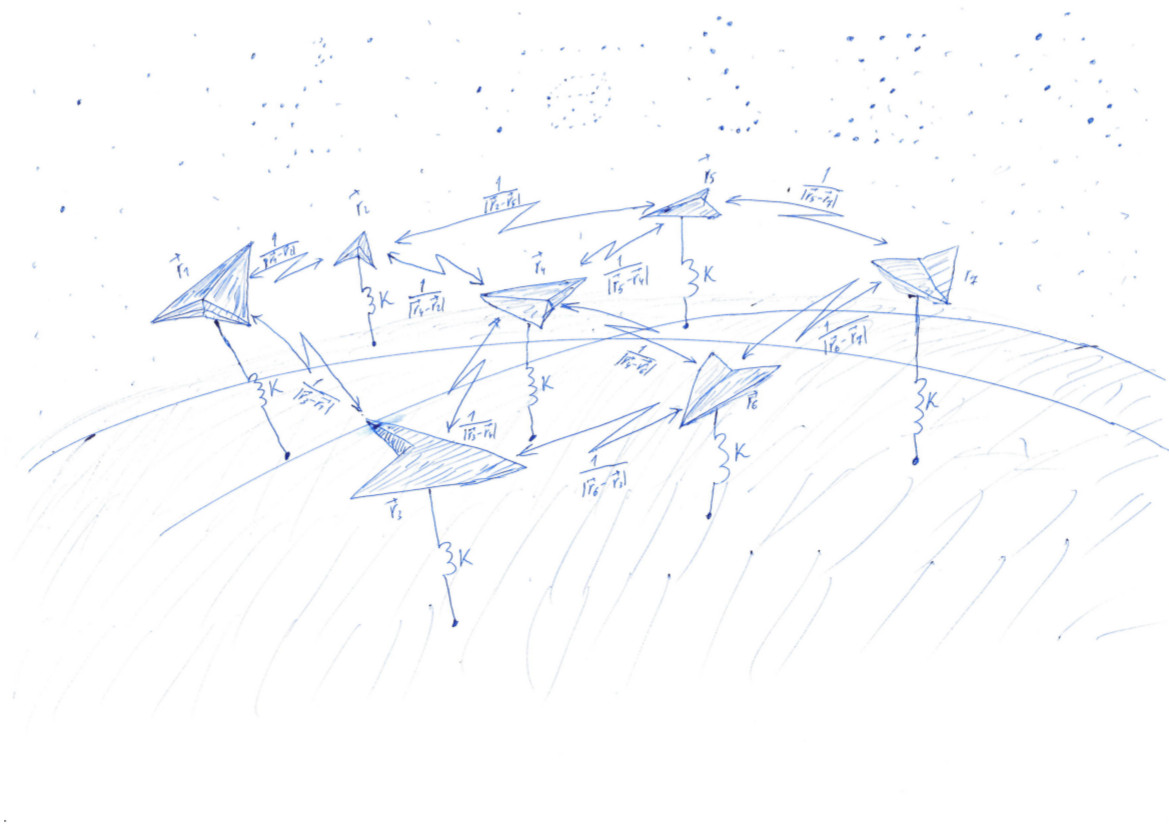
Woher kommt die Aufgabe?

Jeder minimiert seine Funktionalität (c) Anonymer Data Scientist

In einer der vorherigen Veröffentlichungen unseres Blogs , nämlich im Abschnitt "Rake Nr. 6", haben wir über die DSSM-Technologie gesprochen, mit der Sie Text in Vektoren konvertieren können. Um eine solche Abbildung zu finden, muss man die Koeffizienten linearer Transformationen finden, die die ziemlich komplexe Verlustfunktion minimieren. Aufgrund der großen Dimensionalität der Vektoren ist es schwierig zu verstehen, was beim Lernen eines solchen Modells passiert. Um eine Intuition zu entwickeln, mit der Sie die Optimierungsmethode auswählen und die Parameter dieser Methode festlegen können, können Sie eine vereinfachte Version dieser Aufgabe in Betracht ziehen. Lassen Sie die Vektoren nun in unserem üblichen dreidimensionalen Raum sein, dann sind sie leicht zu zeichnen. Und die Verlustfunktion wird das Potenzial sein, die Punkte auseinander zu drücken und die Einheitskugel anzuziehen. In diesem Fall ist die Lösung des Problems eine gleichmäßige Verteilung der Punkte über die Kugel. Die Qualität der aktuellen Lösung lässt sich leicht mit dem Auge beurteilen.

Wir werden also nach einer gleichmäßigen Verteilung über die Sphäre einer bestimmten Menge suchen $$$n$ Punkte. Eine solche Verteilung ist manchmal für die Akustik erforderlich, um zu verstehen, in welche Richtung eine Welle in einem Kristall ausgelöst werden soll. Signalman - um herauszufinden, wie Satelliten in die Umlaufbahn gebracht werden können, um die beste Kommunikationsqualität zu erzielen. Meteorologe - zur Platzierung von Wetterüberwachungsstationen.

Für einige $$$n$ Die Aufgabe ist leicht zu lösen . Zum Beispiel wenn $$$n = 8$ können wir den Würfel nehmen und seine Eckpunkte werden die Antwort auf das Problem sein. Wir haben auch Glück, wenn $$$n$ ist gleich der Anzahl der Eckpunkte des Ikosaeders, Dodekaeders oder eines anderen platonischen Festkörpers. Ansonsten ist die Aufgabe nicht so einfach.

Für eine ausreichend große Anzahl von Punkten gibt es eine Formel mit empirisch ausgewählten Koeffizienten. Hier , hier , hier und hier gibt es mehrere weitere Optionen. Es gibt jedoch eine universellere, wenn auch komplexere Lösung, der dieser Artikel gewidmet ist.

Wir lösen ein Problem, das dem Thomson-Problem ( Wiki ) sehr ähnlich ist. Streuung $$$n$ Punkte zufällig und ziehen sie dann auf eine Oberfläche wie eine Kugel und stoßen sich voneinander ab. Anziehung und Abstoßung werden durch das Funktionspotential bestimmt. Beim Minimalwert der Potentialfunktion liegen die Punkte am gleichmäßigsten auf der Kugel.

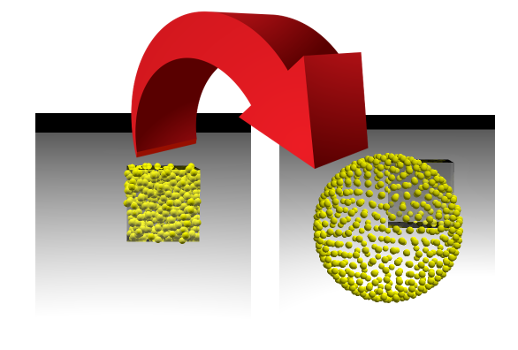
Diese Aufgabe ist dem Lernprozess von ML-Modellen (Machine Learning) sehr ähnlich, bei dem die Verlustfunktion minimiert wird. Aber ein Datenwissenschaftler beobachtet normalerweise, wie eine einzelne Zahl abnimmt, und wir können beobachten, wie sich das Bild ändert. Wenn es uns gelingt, werden wir sehen, wie die zufällig im Würfel platzierten Punkte mit Seite 1 entlang der Oberfläche der Kugel divergieren:

Schematisch kann der Algorithmus zur Lösung des Problems wie folgt dargestellt werden. Jeder Punkt im dreidimensionalen Raum entspricht einer Zeile der Matrix $$$X$ . Die Verlustfunktion wird aus dieser Matrix berechnet. $$$L$ deren Minimalwert einer gleichmäßigen Verteilung der Punkte über die Kugel entspricht. Der Mindestwert wird mithilfe der pytorch und tensorflow , mit denen der Gradient der Verlustfunktion durch die Matrix berechnet werden kann $$$X$ und mit einer der in der Bibliothek implementierten Methoden auf ein Minimum reduzieren: SGD, ADAM, ADAGRAD usw.

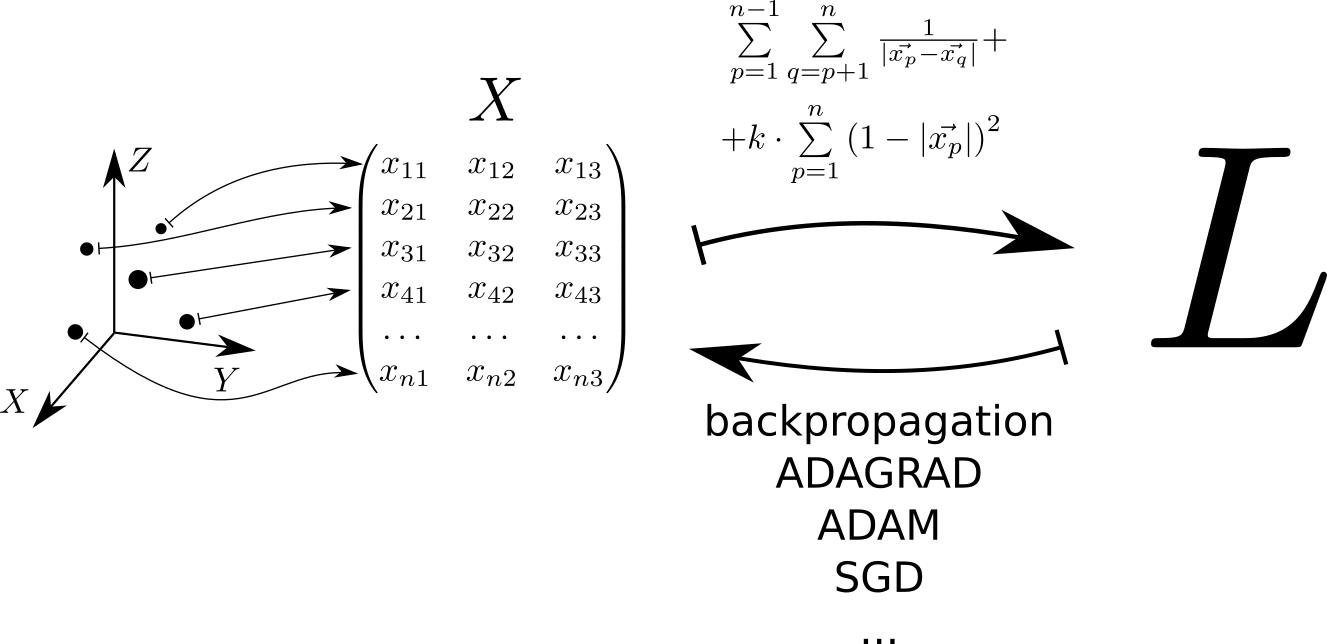
Wir betrachten das Potenzial

Aufgrund seiner Einfachheit, Ausdruckskraft und Fähigkeit, als Schnittstelle zu Bibliotheken zu dienen, die in anderen Sprachen geschrieben sind, wird Python häufig zur Lösung von Problemen des maschinellen Lernens verwendet. Daher sind die Codebeispiele in diesem Artikel in Python geschrieben. Für schnelle Matrixberechnungen verwenden wir die Numpy-Bibliothek. Minimierung der Funktion vieler Variablen - Pytorch und Tensorflow.

Wir streuen zufällig Punkte im Würfel mit Seite 1. Lassen Sie uns 500 Punkte haben, und die elastische Wechselwirkung ist 1000-mal signifikanter als die elektrostatische:

 import numpy as np n = 500 k = 1000 X = np.random.rand(n, 3) 

Dieser Code erzeugte eine Matrix $$$X$ die Größe $$$3 \ mal n$ gefüllt mit Zufallszahlen von 0 bis 1:

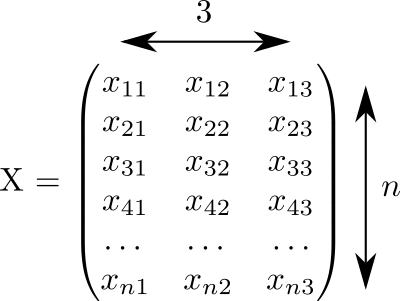
Wir nehmen an, dass jede Zeile dieser Matrix einem Punkt entspricht. Und in drei Spalten werden die Koordinaten aufgezeichnet $$$x, y, z$ alle unsere Punkte.

Das Potential der elastischen Wechselwirkung eines Punktes mit der Oberfläche einer Einheitskugel $$$u_1 = k \ cdot (1 - r) ^ 2/2$ . Potential der elektrostatischen Wechselwirkung von Punkten $$$p$ und $$$q$ - - $$$u_2 = 1 / | r_p - r_q |$ . Das volle Potential besteht aus der elektrostatischen Wechselwirkung aller Punktpaare und der elastischen Wechselwirkung jedes Punktes mit der Oberfläche der Kugel:

$$

$$U (x_1, ..., x_n) = \ Summe \ Grenzen _ {p = 1} ^ {n - 1} \ Summe \ Grenzen _ {q = p + 1} ^ {n} \ frac 1 {\ left | \ vec {x_p} - \ vec {x_q} \ right | } + k \ cdot \ sum \ limitiert _ {p = 1} ^ n \ left (1 - | \ vec {x_p} | \ right) ^ 2 \ rightarrow \ min$$

Grundsätzlich kann der Potentialwert nach folgender Formel berechnet werden:

 L_for = 0 L_for_inv = 0 L_for_sq = 0 for p in range(n): p_distance = 0 for i in range(3): p_distance += x[p, i]**2 p_distance = math.sqrt(p_distance) L_for_sq += k * (1 - p_distance)**2 #     ,     for q in range(p + 1, n): if q != p: pq_distance = 0 for i in range(3): pq_distance += (x[p, i] - x[q, i]) ** 2 pq_distance = math.sqrt(pq_distance) L_for_inv += 1 / pq_distance #      L_for = (L_for_inv + L_for_sq) / n print('loss =', L_for) 

Aber es gibt ein bisschen Ärger. Für erbärmliche 2000 Punkte wird dieses Programm 2 Sekunden lang ausgeführt. Es wird viel schneller sein, wenn wir diesen Wert mit vektorisierten Matrixberechnungen berechnen. Die Beschleunigung wird sowohl durch die Implementierung von Matrixoperationen unter Verwendung der "schnellen" Sprachen fortran und C als auch durch die Verwendung von vektorisierten Prozessoroperationen erreicht, die es ermöglichen, eine Aktion für eine große Menge von Eingabedaten in einem Taktzyklus auszuführen.

Schauen wir uns die Matrix an $$$S = X \ cdot X ^ T$ . Es hat viele interessante Eigenschaften und wird häufig in Berechnungen gefunden, die sich auf die Theorie der linearen Klassifikatoren in ML beziehen. Also, wenn wir das in der Zeile der Matrix annehmen $$$X$ mit Indizes $$$p$ und $$$q$ Es werden dreidimensionale Raumvektoren geschrieben $$$\ vec {r _ p}, \ vec {r_q}$ dann die Matrix $$$S$ wird aus skalaren Produkten dieser Vektoren bestehen. Solche Vektoren $$$n$ Stücke, dann die Dimension der Matrix $$$S$ ist gleich $$$n \ times n$ .

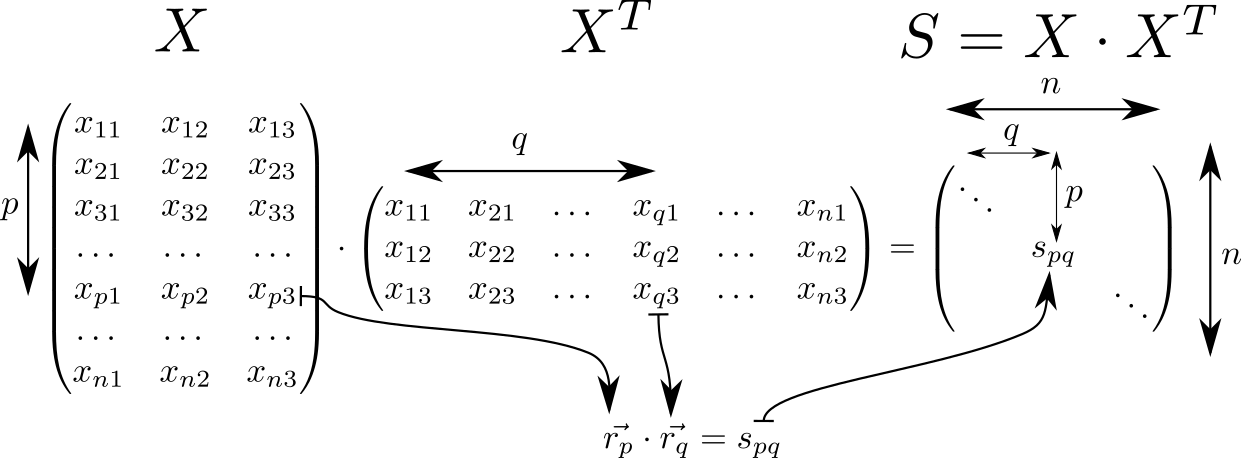
Auf der Diagonale der Matrix $$$S$ stehen Quadrate von Vektorlängen $$$\ vec {r_p}: s_ {p p} = r_p ^ 2$ . Wenn wir dies wissen, betrachten wir das volle Potenzial der Interaktion. Wir beginnen mit der Berechnung von zwei Hilfsmatrizen. In einer diagonalen Matrix $$$S$ wird in Zeilen, in anderen - in Spalten wiederholt.

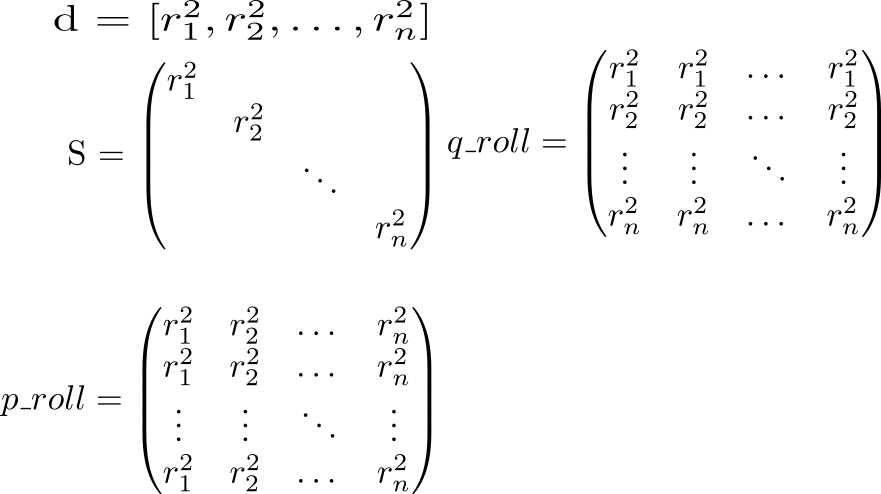
Betrachten wir nun den Wert des Ausdrucks p_roll + q_roll - 2 * S

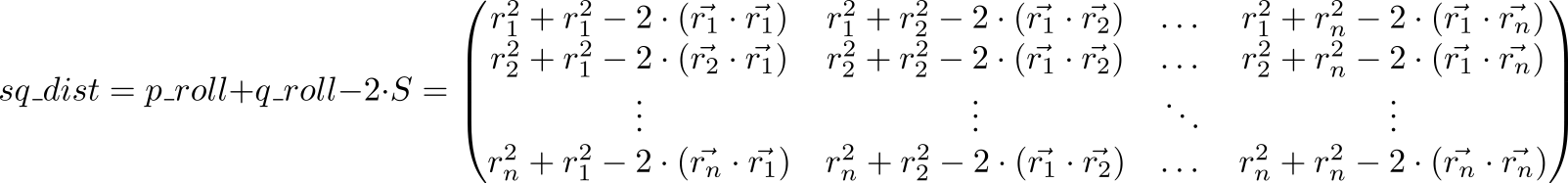
Indizierter Artikel $$$(p, q)$ Matrix sq_dist ist gleich $$$r_p ^ 2 + r_q ^ 2 - 2 \ cdot (\ vec {r_p}, \ vec {r_q}) = (\ vec {r_p} - \ vec {r_q}) ^ 2$ . Das heißt, wir haben eine Matrix von Quadraten von Abständen zwischen Punkten.

Elektrostatische Abstoßung auf einer Kugel

dist = np.sqrt(sq_dist) - Matrix der Abstände zwischen Punkten. Wir müssen das Potential unter Berücksichtigung der Abstoßung von Punkten zwischen sich und der Anziehung zur Kugel berechnen. Setzen Sie die Einheiten auf die Diagonale und ersetzen Sie jedes Element durch die Umkehrung (denken Sie nur nicht, dass wir die Matrix invertieren!): rec_dist_one = 1 / (dist + np.eye(n)) . Das Ergebnis ist eine Matrix, auf deren Diagonale sich Einheiten befinden, andere Elemente sind die Potentiale der elektrostatischen Wechselwirkung zwischen den Punkten.

Nun fügen wir der Oberfläche der Einheitskugel das quadratische Anziehungspotential hinzu. Der Abstand von der Oberfläche der Kugel $$$(1 - r)$ . Quadrieren Sie es und multiplizieren Sie es mit $$$k$ , die die Beziehung zwischen der Rolle der elektrostatischen Abstoßung von Partikeln und der Anziehung einer Kugel definiert. Gesamt k = 1000 , all_interactions = rec_dist_one - torch.eye(n) + (d.sqrt() - torch.ones(n))**2 . Die lang erwartete Verlustfunktion, die wir minimieren werden: t = all_interactions.sum()

Ein Programm, das das Potenzial mithilfe der Numpy-Bibliothek berechnet:

 S = X.dot(XT) #    pp_sq_dist = np.diag(S) #  p_roll = pp_sq_dist.reshape(1, -1).repeat(n, axis=0) #     q_roll = pp_sq_dist.reshape(-1, 1).repeat(n, axis=1) #     pq_sq_dist = p_roll + q_roll - 2 * S #      pq_dist = np.sqrt(pq_sq_dist) #    pp_dist = np.sqrt(pp_sq_dist) #      surface_dist_sq = (pp_dist - np.ones(n)) ** 2 #       rec_pq_dist = 1 / (pq_dist + np.eye(n)) - np.eye(n) #      L_np_rec = rec_pq_dist.sum() / 2 #     L_np_surf = k * surface_dist_sq.sum() #       L_np = (L_np_rec + L_np_surf) / n #   ,     print('loss =', L_np) 

Hier sieht es etwas besser aus - 200 ms bei 2000 Punkten.

Wir verwenden Pytorch:

 import torch pt_x = torch.from_numpy(X) # pt_x -   tensor   pytorch pt_S = pt_x.mm(pt_x.transpose(0, 1)) # mm - matrix multiplication pt_pp_sq_dist = pt_S.diag() pt_p_roll = pt_pp_sq_dist.repeat(n, 1) pt_q_roll = pt_pp_sq_dist.reshape(-1, 1).repeat(1, n) pt_pq_sq_dist = pt_p_roll + pt_q_roll - 2 * pt_S pt_pq_dist = pt_pq_sq_dist.sqrt() pt_pp_dist = pt_pp_sq_dist.sqrt() pt_surface_dist_sq = (pt_pp_dist - torch.ones(n, dtype=torch.float64)) ** 2 pt_rec_pq_dist = 1/ (pt_pq_dist + torch.eye(n, dtype=torch.float64)) - torch.eye(n, dtype=torch.float64) L_pt = (pt_rec_pq_dist.sum() / 2 + k * pt_surface_dist_sq.sum()) / n print('loss =', float(L_pt)) 

Und schließlich Tensorflow:

 import tensorflow as tf tf_x = tf.placeholder(name='x', dtype=tf.float64) tf_S = tf.matmul(tf_x, tf.transpose(tf_x)) tf_pp_sq_dist = tf.diag_part(tf_S) tf_p_roll = tf.tile(tf.reshape(tf_pp_sq_dist, (1, -1)), (n, 1)) tf_q_roll = tf.tile(tf.reshape(tf_pp_sq_dist, (-1, 1)), (1, n)) tf_pq_sq_dist = tf_p_roll + tf_q_roll - 2 * tf_S tf_pq_dist = tf.sqrt(tf_pq_sq_dist) tf_pp_dist = tf.sqrt(tf_pp_sq_dist) tf_surface_dist_sq = (tf_pp_dist - tf.ones(n, dtype=tf.float64)) ** 2 tf_rec_pq_dist = 1 / (tf_pq_dist + tf.eye(n, dtype=tf.float64)) - tf.eye(n, dtype=tf.float64) L_tf = (tf.reduce_sum(tf_rec_pq_dist) / 2 + k * tf.reduce_sum(tf_surface_dist_sq)) / n glob_init = tf.local_variables_initializer() #     with tf.Session() as tf_s: #     glob_init.run() #   res, = tf_s.run([L_tf], feed_dict={tf_x: x}) #   print(res) 

Vergleichen Sie die Leistung dieser drei Ansätze:

N.	Python	numpy	Pytorch	Tensorflow
2000	4.03	0,083	1.11	0,205
10.000	99	2.82	2.18	7.9

Vektorisierte Berechnungen ergeben einen Gewinn von mehr als eineinhalb Dezimalstellen relativ zu reinem Python-Code. Die "Kesselplatte" in Pytorch ist sichtbar: Berechnungen mit kleinem Volumen nehmen spürbar viel Zeit in Anspruch, ändern sich jedoch mit zunehmendem Rechenvolumen fast nicht.

Visualisierung

Heutzutage können Daten mit einer Vielzahl von Paketen wie Matlab, Wolfram Mathematica, Maple, Matplotlib usw. visualisiert werden. In diesen Paketen gibt es viele komplexe Funktionen, die komplexe Aufgaben ausführen. Wenn Sie vor einer einfachen, aber nicht standardmäßigen Aufgabe stehen, sind Sie leider unbewaffnet. Meine Lieblingslösung in dieser Situation ist Povray. Dies ist ein sehr leistungsfähiges Programm, das normalerweise zum Erstellen fotorealistischer Bilder verwendet wird, aber als "Assembler der Visualisierung" verwendet werden kann. Egal wie schwierig die Oberfläche ist, die Sie anzeigen möchten, bitten Sie povray normalerweise, Kugeln mit auf dieser Oberfläche liegenden Zentren zu zeichnen.

Mit der Vapory-Bibliothek können Sie eine Povray-Szene direkt in Python erstellen, rendern und das Ergebnis anzeigen. Jetzt sieht es so aus:

Das Bild wird wie folgt erhalten:

 import vapory from PIL import Image def create_scene(moment): angle = 2 * math.pi * moment / 360 r_camera = 7 camera = vapory.Camera('location', [r_camera * math.cos(angle), 1.5, r_camera * math.sin(angle)], 'look_at', [0, 0, 0], 'angle', 30) light1 = vapory.LightSource([2, 4, -3], 'color', [1, 1, 1]) light2 = vapory.LightSource([2, 4, 3], 'color', [1, 1, 1]) plane = vapory.Plane([0, 1, 0], -1, vapory.Pigment('color', [1, 1, 1])) box = vapory.Box([0, 0, 0], [1, 1, 1], vapory.Pigment('Col_Glass_Clear'), vapory.Finish('F_Glass9'), vapory.Interior('I_Glass1')) spheres = [vapory.Sphere( [float(r[0]), float(r[1]), float(r[2])], 0.05, vapory.Texture(vapory.Pigment('color', [1, 1, 0]))) for r in x] return vapory.Scene(camera, objects=[light1, light2, plane, box] + spheres, included=['glass.inc']) for t in range(0, 360): flnm = 'out/sphere_{:03}.png'.format(t) scene = create_scene(t) scene.render(flnm, width=800, height=600, remove_temp=False) clear_output() display(Image.open(flnm)) 

Aus einer Reihe von Dateien werden mit ImageMagic animierte Gifs zusammengestellt:

 convert -delay 10 -loop 0 sphere_*.png sphere_all.gif 

Auf github sehen Sie den Arbeitscode , dessen Fragmente hier angegeben sind. Im zweiten Artikel werde ich darüber sprechen, wie die Funktion minimiert werden kann, damit die Punkte aus dem Würfel herauskommen und sich gleichmäßig über die Kugel verteilen.