Es gibt eine Reihe von Aufgaben, bei denen der Bereich der Ausgabewerte begrenzt werden sollte, während die Eingabedaten dies nicht garantieren können. Neben erzwungenen Situationen kann die Signalbegrenzung eine zielorientierte Aufgabe sein, beispielsweise beim Komprimieren eines Signals oder beim Implementieren des „Overdrive“ -Effekts.
Die einfachste Implementierung einer Einschränkung besteht darin, sie auf einen bestimmten Wert zu zwingen, wenn ein bestimmtes Niveau überschritten wird. Zum Beispiel sieht es für eine Sinuskurve mit zunehmender Amplitude folgendermaßen aus:

Hier fungiert die Clip-Funktion als Begrenzer, als Argument, von dem das Eingangssignal und die Restriktionsparameter übertragen werden, und das Ergebnis der Funktion ist das Ausgangssignal.
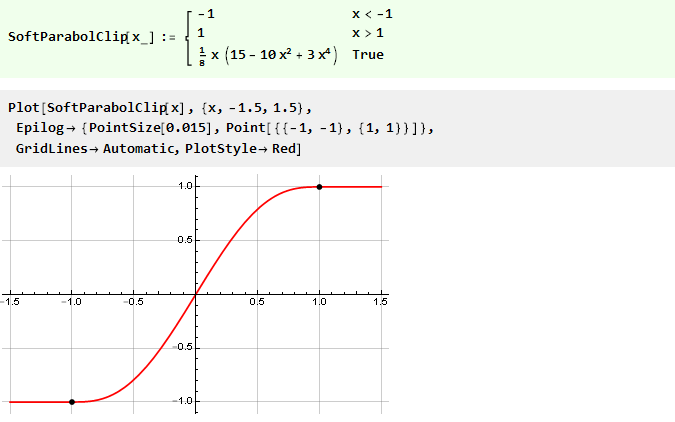
Schauen wir uns das Clip-Funktionsdiagramm separat an:
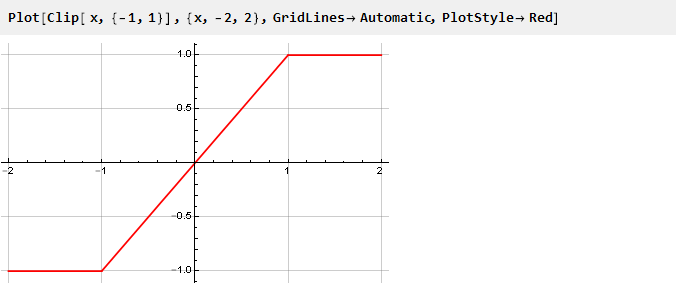
Daraus ist ersichtlich, dass der Ausgangswert zwar dem Grenzwert nicht entspricht, der Ausgangswert jedoch dem Eingang entspricht und sich das Signal nicht ändert. Bei Überschreitung hängt der Ausgabewert in keiner Weise vom Eingang ab und bleibt auf dem gleichen Niveau. Tatsächlich haben wir eine stückweise stetige Funktion, die aus drei anderen besteht: y = -1, y = x und y = 1, die je nach Argument ausgewählt wird und der folgenden Notation entspricht:

Der Übergang zwischen Funktionen erfolgt ziemlich abrupt; und sieht verlockend aus, es glatter zu machen. Mathematisch ist diese Schärfe darauf zurückzuführen, dass die Ableitungen der Funktionen an den Andockpunkten nicht übereinstimmen. Dies ist leicht zu erkennen, wenn Sie die Ableitung der Clip-Funktion zeichnen:
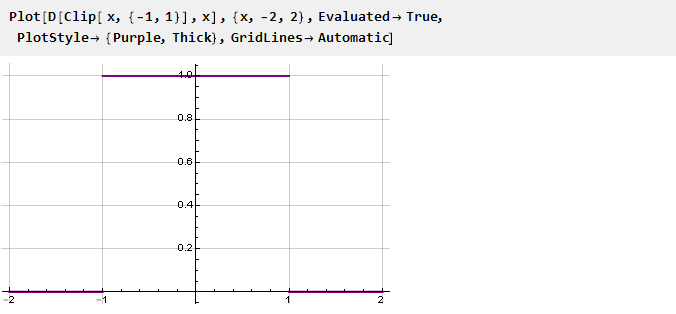
Um die Glätte der Beschränkungsfunktion sicherzustellen, ist es daher notwendig, die Gleichheit der Ableitungen an den Verbindungspunkten sicherzustellen. Und da die Extremfunktionen, die wir haben, Konstanten sind, deren Ableitungen gleich Null sind, müssen auch die abgeleiteten Restriktionsfunktionen an den Andockpunkten gleich Null sein. Als nächstes werden wir einige dieser Funktionen betrachten, die ein reibungsloses Andocken gewährleisten.
Sinus
Am einfachsten ist es, die sin-Funktion für das Intervall von -pi / 2 bis pi / 2 zu verwenden, an dessen Grenzen die Werte der Ableitung per Definition gleich Null sind:
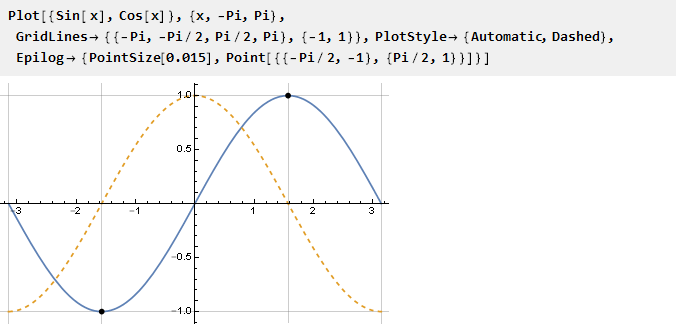
Sie müssen die Argumente nur so skalieren, dass die Einheit auf den Pi / 2 projiziert wird. Jetzt können wir die Begrenzungsfunktion selbst definieren:

Und baue ihren Zeitplan auf:
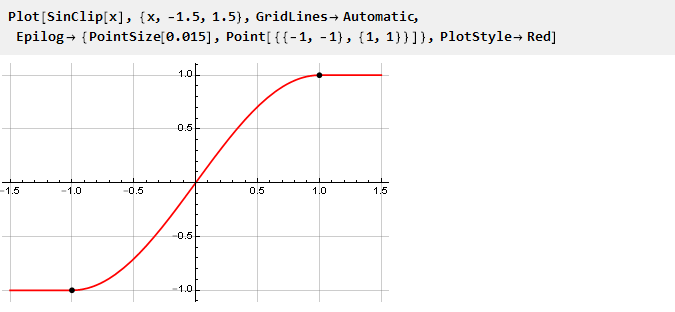
Da die Grenzen unserer Einschränkung streng definiert sind, wird die Einschränkung durch Skalieren des Eingangssignals mit anschließender (falls erforderlich) Rückskalierung festgelegt.
Es gibt auch keine Situation mehr, in der das Eingangssignal ohne Verzerrung zum Ausgang übertragen wird - je niedriger der Verstärkungspegel, desto geringer der Verzerrungspegel aufgrund von Einschränkungen -, aber das Signal ist in jedem Fall verzerrt.
Die Auswirkung des Verstärkungsparameters auf die Signalverzerrung ist auch in der Dynamik zu sehen:

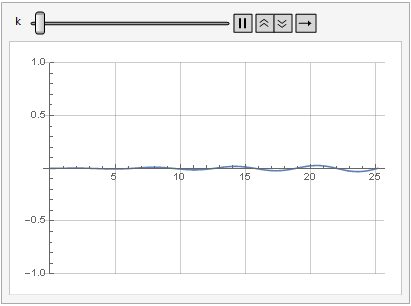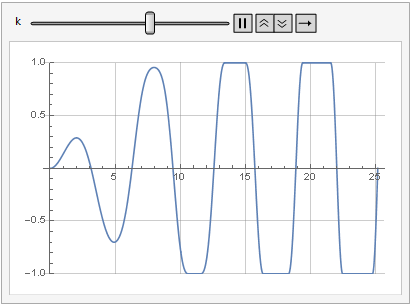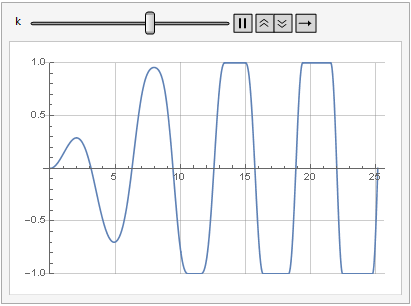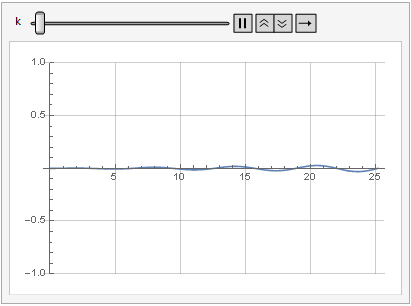
Mehr Glätte
Schauen wir uns die Ableitung unserer Funktion an:
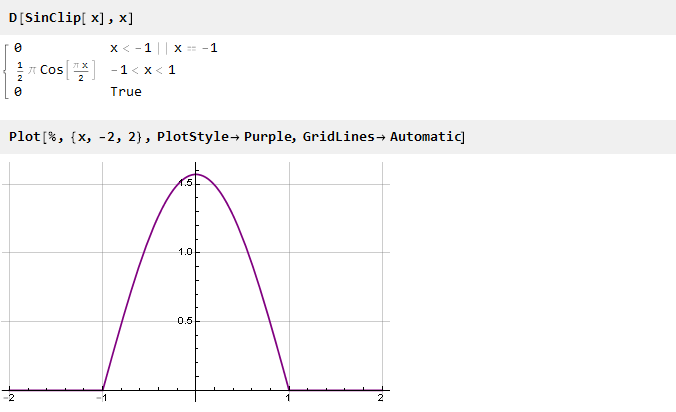
Es gibt keine Lücken mehr in den Werten, aber es gibt Lücken in der Ableitung (die zweite, wenn wir von der ursprünglichen Funktion zählen). Um dies zu beseitigen, können Sie den umgekehrten Weg gehen: Bilden Sie zuerst eine glatte Ableitung und integrieren Sie sie dann, um die gewünschte Funktion zu erhalten.
Der einfachste Weg, die Ableitung an den Punkten -1 und 1 aufzuheben, besteht darin, die Funktion einfach zu quadrieren - alle negativen Werte der Funktion werden positiv und dementsprechend treten an den Schnittpunkten der Funktion Beugungen mit Null auf.
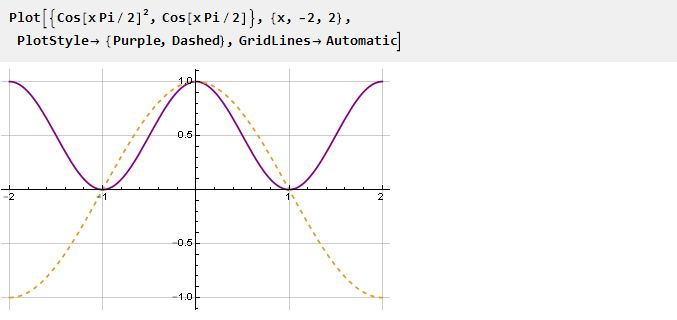
Finden Sie das Antiderivativ:
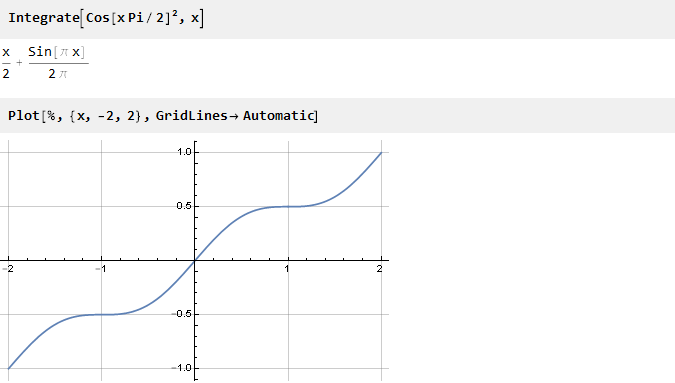
Jetzt bleibt es, um es entlang der Ordinatenachse zu skalieren. Finden Sie dazu den Wert unter Punkt 1:

Und dividiere es (ja, speziell hier ist es eine elementare Multiplikation mit 2, aber das passiert nicht immer):

Somit hat die endgültige Beschränkungsfunktion die Form:
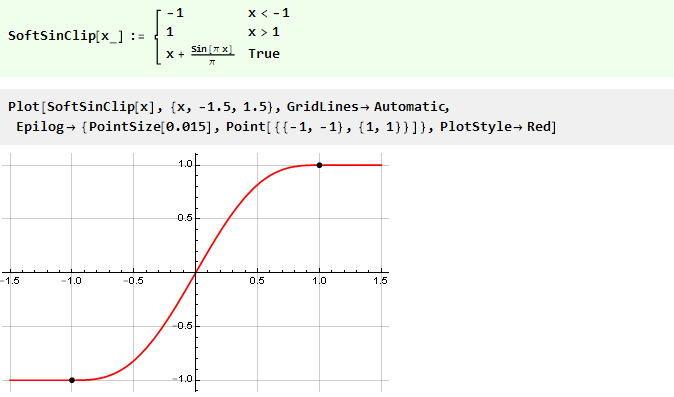
Wir gehen zu Polynomen über
Die Verwendung trigonometrischer Funktionen kann in einigen Fällen etwas verschwenderisch sein. Daher werden wir versuchen, die benötigte Funktion aufzubauen und dabei im Rahmen elementarer mathematischer Operationen zu bleiben.
Betrachten Sie die Parabel:
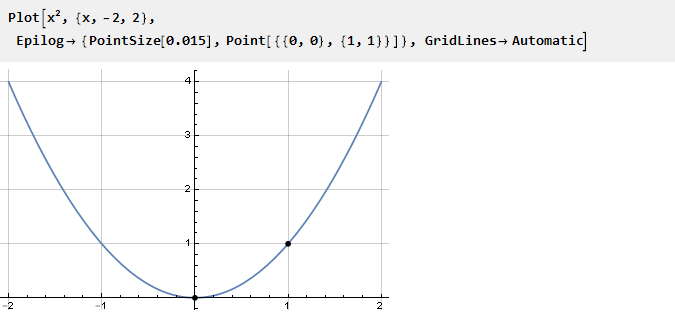
Da es am Punkt Null bereits eine Beugung hat, können wir denselben Teil im Intervall {0,1} zum Andocken an Konstanten verwenden. Für negative Werte muss es nach unten und links verschoben werden:

und für positiv - vertikal und horizontal reflektieren:

Und unsere Funktion mit einer Parabel wird die Form annehmen:
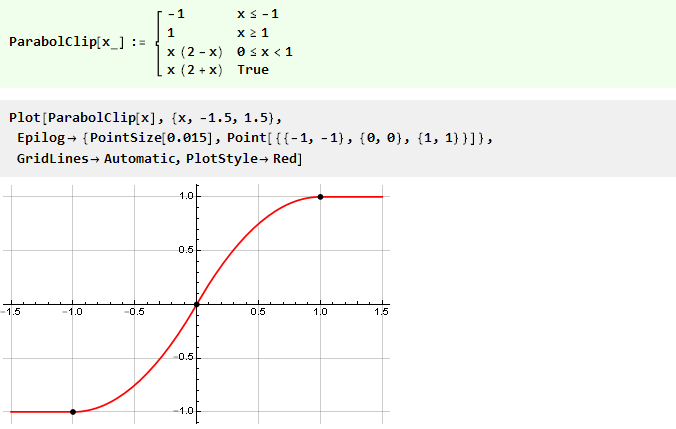
Lassen Sie uns etwas komplizieren
Gehen wir zurück zu unserer Parabel, drehen sie um und verschieben sie um eine Einheit:
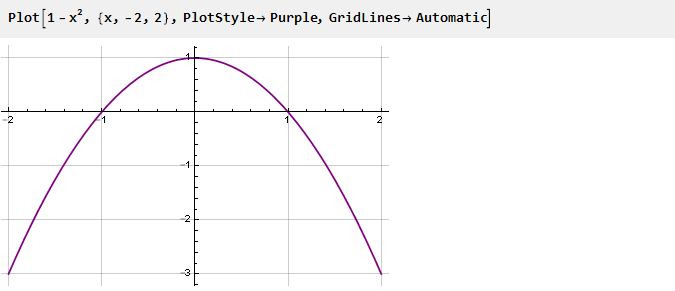
Dies wird eine Ableitung unserer Funktion sein. Um es an den Verbindungspunkten glatter zu machen, werden wir die zweite Ableitung auf folgende Weise auf Null setzen:
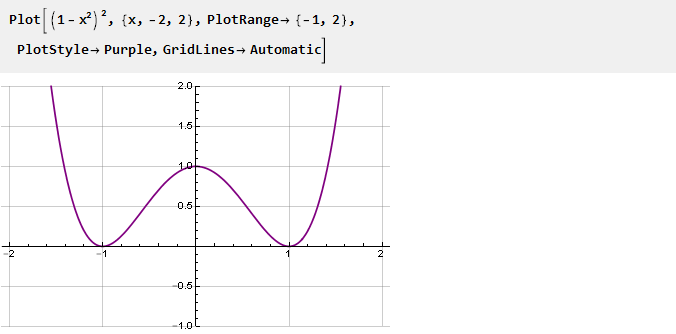
Integrieren und skalieren:

Wir erhalten eine noch flüssigere Funktion:
Mehr Geschmeidigkeit für den Gott der Geschmeidigkeit
Hier versuchen wir, bei noch höheren Derivaten Glätte an den Andockpunkten zu erreichen. Dazu definieren wir zunächst die Funktion als Polynom mit unbekannten Koeffizienten und versuchen, die Koeffizienten durch eine Lösung des Gleichungssystems zu finden.
Beginnen wir mit der 1. Ableitung:

2. Platz:

3. Platz:

Alle diese Koeffizienten sehen aus, als hätten sie eine Art Logik. Wir schreiben die Faktoren auf und multiplizieren sie mit dem Wert des Grades bei x; und um nicht jedes Mal dasselbe zu schreiben, automatisieren wir den Prozess des Findens der Koeffizienten:
 Es sieht aus wie
Es sieht aus wie Binomialkoeffizienten. Wir gehen mutig davon aus, dass dies der Fall ist, und schreiben auf dieser Grundlage die verallgemeinerte Formel:

Überprüfen Sie:
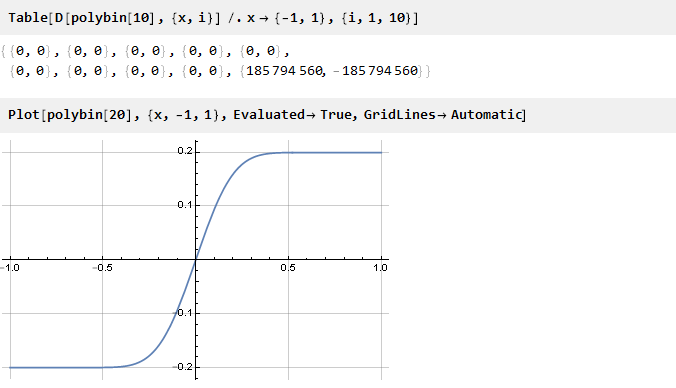
Es scheint wahr zu sein
[1] . Es bleibt nur die Berechnung des Skalierungsfaktors, um die Kanten zur Einheit zu bringen:

Und nach Skalierung und Vereinfachung stellen wir fest, dass unsere mathematischen Kenntnisse etwas veraltet sind
[2] :
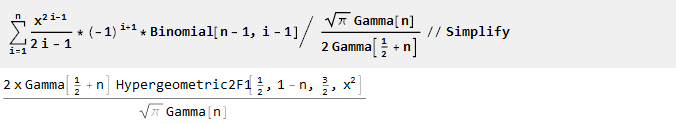
Somit haben wir eine Erzeugungsfunktion der Ordnung n erhalten, in der n-1 der ersten Ableitungen gleich Null ist:

Mal sehen, was passiert ist:
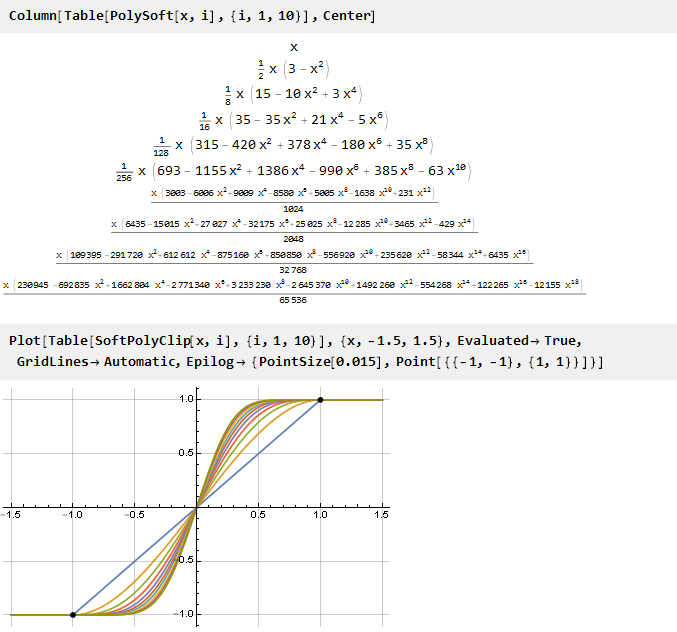
Und da sich unsere verallgemeinerte Formel als stetig herausgestellt hat, können Sie nicht ganzzahlige Parameterwerte verwenden, wenn Sie dies wünschen:
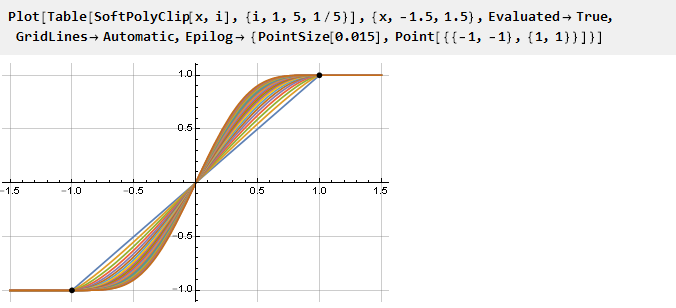
Sie können auch Diagramme von Derivaten erstellen, die auf eine Skala reduziert sind:
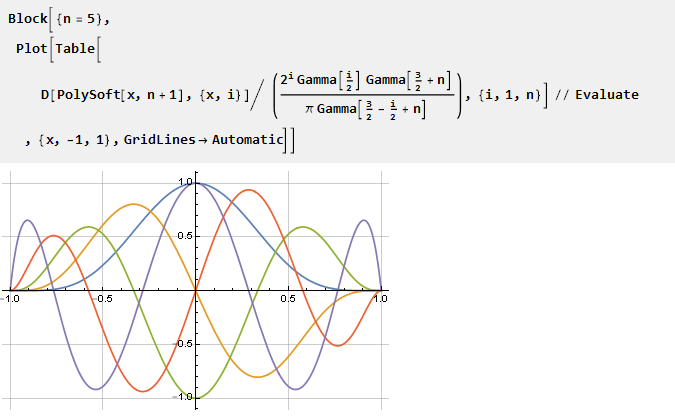
Steifheit hinzufügen
Es wäre verlockend, den Grad der „Starrheit“ der Beschränkung anpassen zu können.
Kehren wir zu unserer umgekehrten Parabel zurück und fügen einen Koeffizienten mit dem Grad x hinzu:

Je größer n ist, desto größer ist unsere Ableitung "quadratisch" und ihr Antiderivativ ist jeweils scharf:
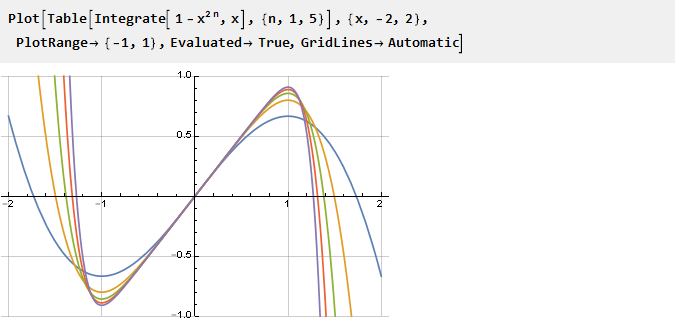
Wir berechnen das Antiderivativ und passen die Skala an:

Versuchen wir nun, den Bruchschritt für den Parameter festzulegen:
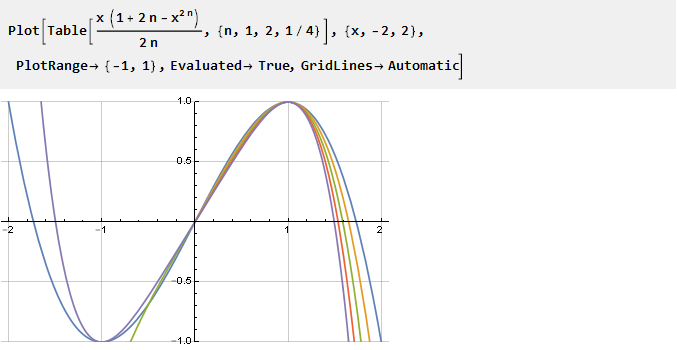
Wie Sie sehen, haben nicht alle n im negativen Teil die richtige Lösung, aber die für uns notwendigen Bedingungen sind im rechten (positiven) Teil noch erfüllt - daher können wir sie für negative Werte einfach invertiert mit einem umgekehrten Argument verwenden. Und da der Definitionsbereich des Parameters nicht mehr nur auf positive ganze Zahlen beschränkt ist, können wir die Formel vereinfachen, indem wir 2n durch n ersetzen:

Wenn Sie n durch n-1 ersetzen, können Sie die Formel etwas schöner machen:
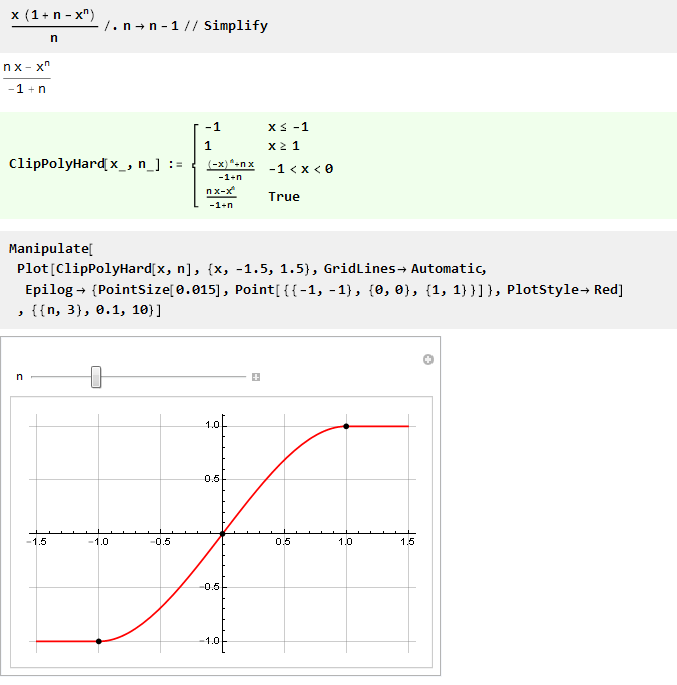
Da wir für n gleich eins eine Division durch Null erhalten, versuchen Sie, die Grenze zu finden:

Die Grenze ist gefunden, was bedeutet, dass wir jetzt
[3] die Funktion für n zu 1 hinzufügen und sie für alle n großen Nullen berücksichtigen können:
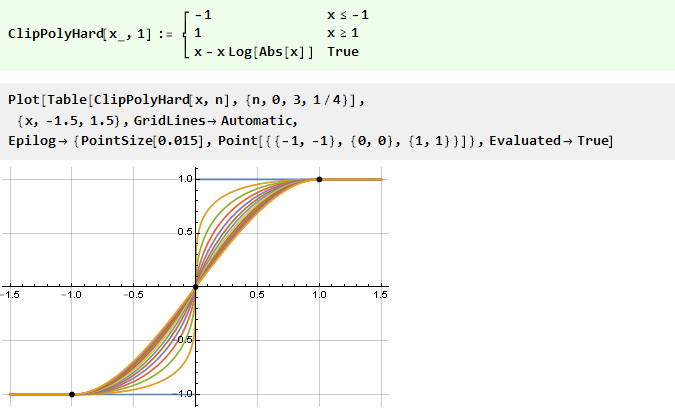
Wenn wir unsere umgekehrte Parabel anfänglich quadrieren, erhalten wir eine noch glattere Funktion:
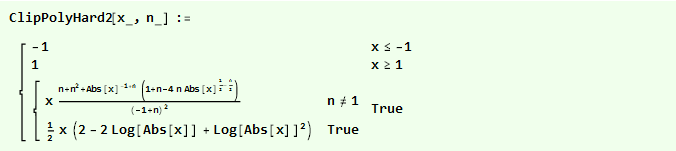
Und wir können sie auf einem Diagramm vergleichen:
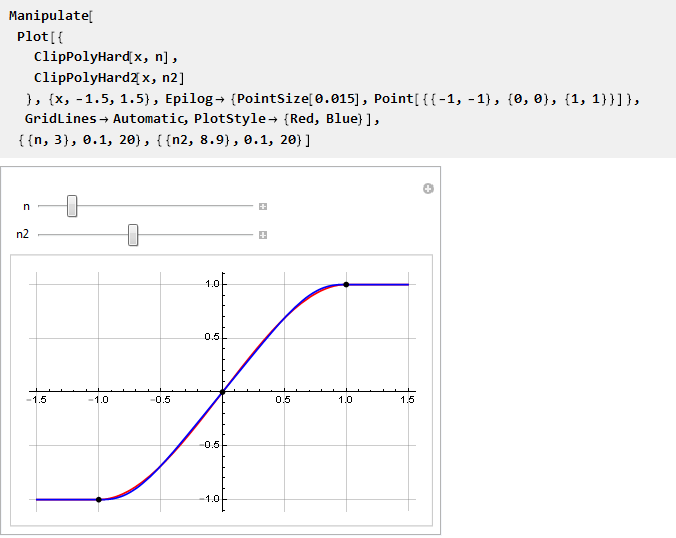
Optimieren Sie es
Schauen wir uns die folgende Funktion an:
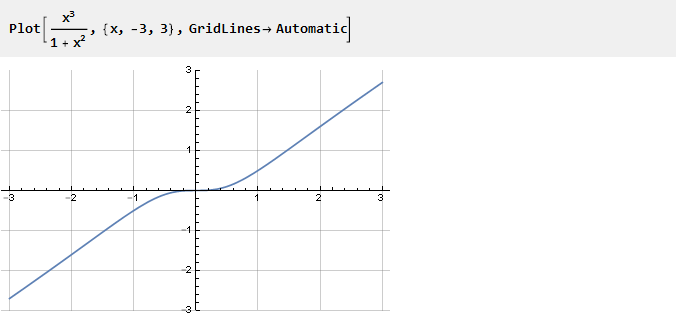
Sie erschien nicht zufällig.
Wenn Sie eine Einheit daraus entfernen, zieht sich x
2 zusammen und nur x bleibt, dh eine geneigte Linie. Je kleiner der Wert von x ist, desto größer ist der Einfluss der Einheit auf den Nenner, wodurch die Krümmung entsteht, die wir benötigen. Wenn Sie diese Funktion in verschiedenen Maßstäben betrachten, können Sie den Grad dieser Krümmung steuern:

Somit können wir die vorherige Funktion mit Steifigkeitskontrolle unter Verwendung nur eines rationalen Polynoms 3-Ordnung umschreiben:
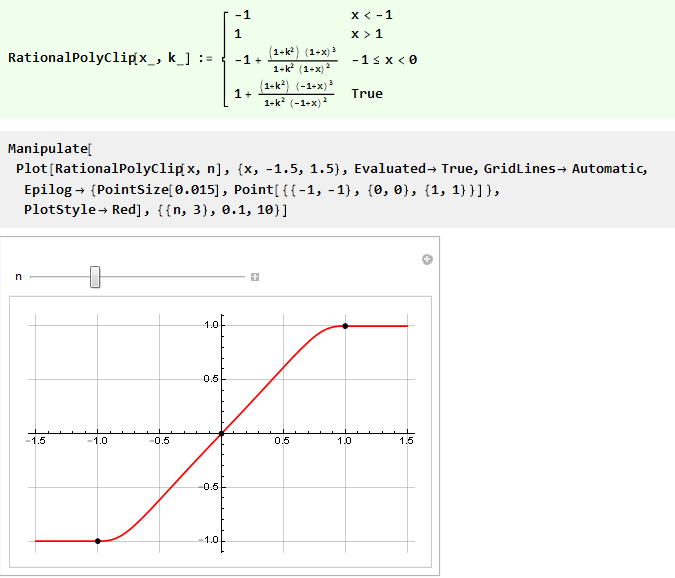
Automatisieren Sie es
Um nicht jedes Mal stückweise kontinuierliche Funktionen anzugeben, können wir eine Hilfsfunktion definieren, die dies selbst ausführt und eine Spenderfunktion als Argument als Eingabe verwendet.
Wenn unsere Funktion bereits diagonale Symmetrie aufweist und auf das Koordinatenzentrum ausgerichtet ist (wie eine Sinuswelle), können wir dies einfach tun
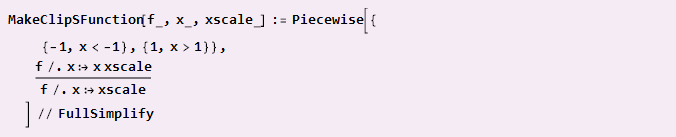
Anwendungsbeispiel:

Wenn Sie wie bei einer Parabel aus Teilen zusammensetzen müssen und der Koordinatenmittelpunkt die Andockpunkte bestimmt, ist die Formel etwas komplizierter:
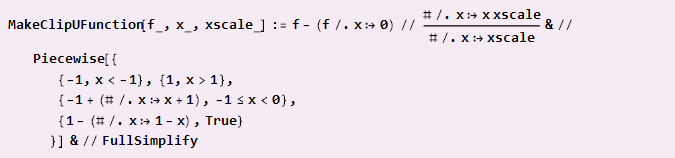
Anwendungsbeispiel:

Gehen wir weiter zum Aussteller
Absolut jede Funktion kann ein Spender sein, um dieses Problem zu lösen. Sie müssen sie nur mit Wendepunkten versehen. Nehmen wir zum Beispiel den um eins nach unten verschobenen Exponenten:
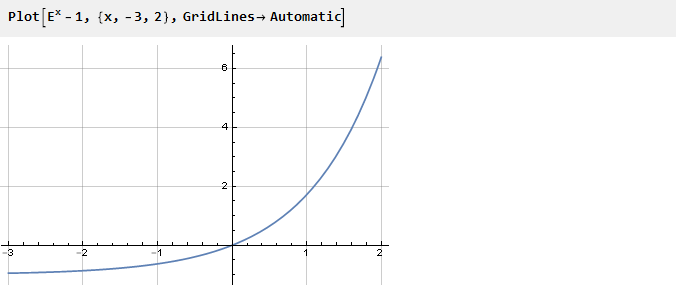
Zuvor haben wir die Funktion quadriert, um die erforderliche Beugung am Punkt Null sicherzustellen. Sie können aber auch den anderen Weg gehen - zum Beispiel mit einer anderen Funktion zusammenfassen, deren Ableitung am Punkt Null im Vorzeichen der Ableitung des Exponenten entgegengesetzt ist. Zum Beispiel -x:
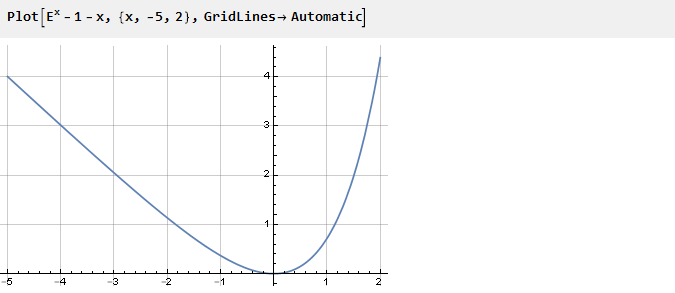
Abhängig davon, auf welcher Seite wir die Kurve nehmen, hängt die endgültige Form der Funktion davon ab. Wenn wir nun die zuvor definierte Hilfsfunktion verwenden und eine der Seiten auswählen, erhalten wir:

Entweder

Und jetzt können wir sie auf einem Diagramm vergleichen:
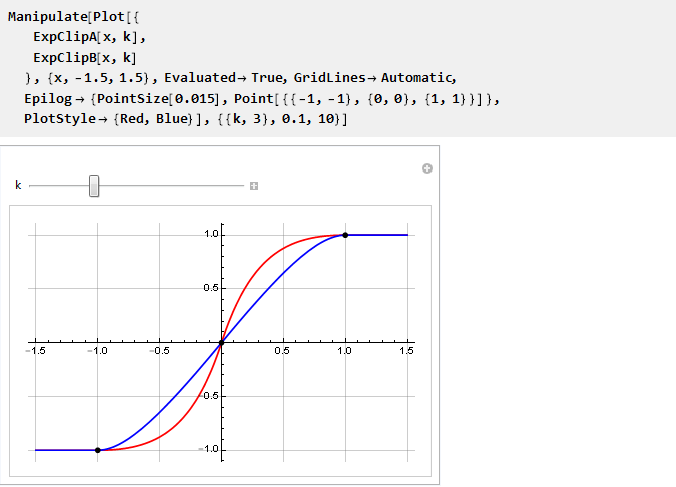
Es ist zu sehen, dass sie als k → 0 dazu neigen, zusammenzufallen; und da wir ihre Werte nicht direkt berechnen können, da wir durch Null dividiert werden, werden wir die Grenze verwenden:

Und sie haben die stückweise Funktion aus der uns bereits bekannten Parabel erhalten.
Symmetrie brechen
Bisher haben wir ausschließlich symmetrische Funktionen betrachtet. Es gibt jedoch Zeiten, in denen wir keine Symmetrie benötigen - zum Beispiel, um Verzerrungen im Klang von Röhrenverstärkern zu simulieren.
Nehmen Sie den Exponenten und multiplizieren Sie ihn mit einer umgekehrten Parabel im Quadrat - um den Schnittpunkt mit der Abszissenachse an den Punkten -1 und 1 zu erhalten und gleichzeitig die Glätte der zweiten Ableitung sicherzustellen; Die Parametrisierung ist durch Skalierung des Exponentenarguments möglich:
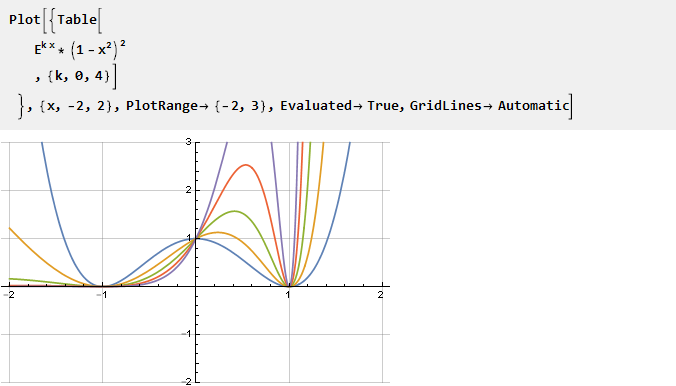
Finden Sie das Antiderivativ und skalieren Sie es:
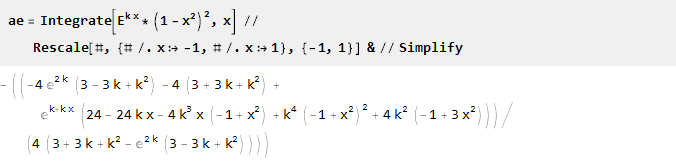
Da für k = 0 erhalten wir die Division durch Null:

Dann finden wir zusätzlich die Grenze,

Das ist ein glattes Polynom dritter Ordnung, das uns bereits bekannt ist. Wenn wir alles zu einer Funktion kombinieren, erhalten wir
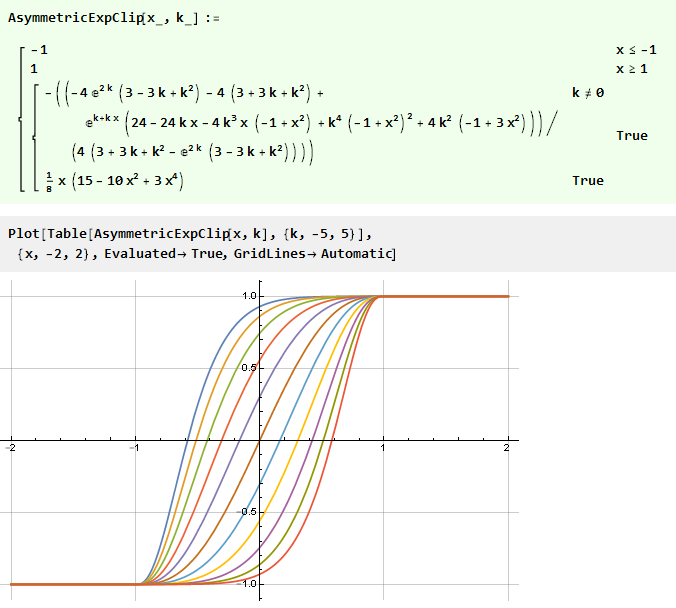
Anstatt zunächst eine asymmetrische Funktion zu entwerfen, können Sie auch in die andere Richtung gehen: Verwenden Sie die vorgefertigte Symmetrie, aber „biegen“ Sie den Wert dieser Funktion mithilfe einer zusätzlichen Kurvenfunktion, die im Intervall {-1,1} definiert ist.
Stellen Sie sich zum Beispiel eine Hyperbel vor:
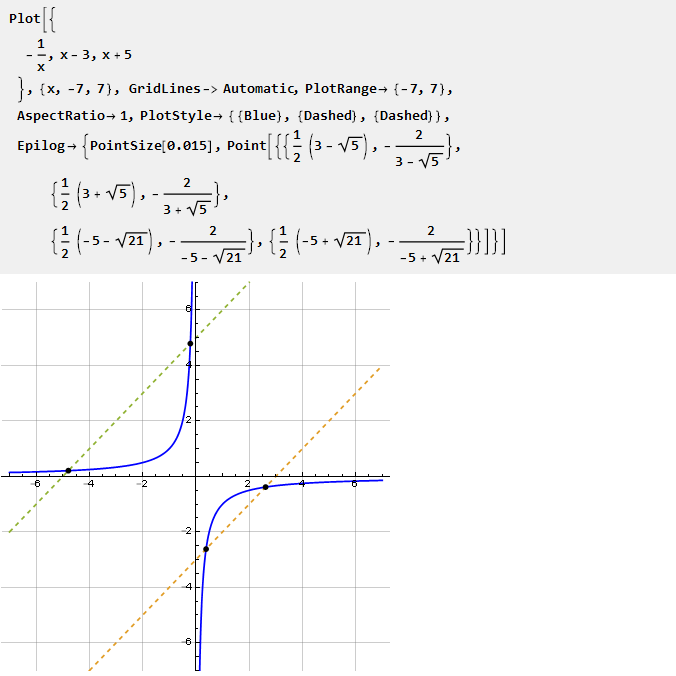
Wenn Sie das Segment in verschiedenen Maßstäben betrachten, können Sie den Krümmungsgrad in beide Richtungen anpassen. Wie finde ich dieses Segment? Anhand des Diagramms könnte man nach dem Schnittpunkt der Hyperbel mit der Linie suchen. Da eine solche Kreuzung jedoch nicht immer existiert, entstehen einige Schwierigkeiten. Deshalb werden wir den anderen Weg gehen.
Fügen Sie der Hyperbel zunächst Skalierungsfaktoren hinzu:

dann werden wir ein Gleichungssystem zusammenstellen, das die Bedingungen für den Durchgang einer Hyperbel durch bestimmte Punkte definiert - und seine Lösung wird die für uns interessanten Koeffizienten angeben:

Ersetzen Sie nun die Lösung durch die ursprüngliche Formel und vereinfachen Sie:

Mal sehen, was wir bekommen, abhängig vom Parameter k:
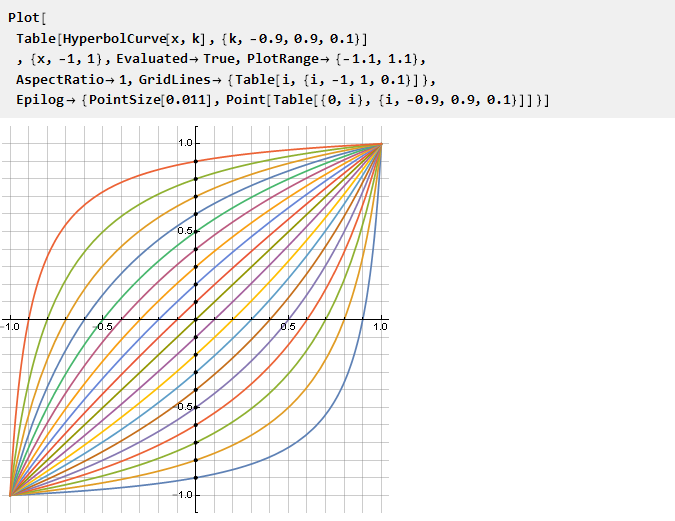
Es ist bemerkenswert, dass für k = 0 die Formel natürlich bei x zusammenbricht und keine besonderen Situationen auftreten - obwohl dies in Bezug auf die anfängliche Übertreibung einem Segment mit der Länge Null und zwei auf einmal entspricht. Es ist nicht weniger bemerkenswert, dass die dazu inverse Funktion dieselbe ist, jedoch mit einem negativen Parameter k:

Jetzt können wir damit eine beliebige Bedingungsfunktion modifizieren, und der Parameter k setzt somit den Schnittpunkt mit der Ordinatenachse:
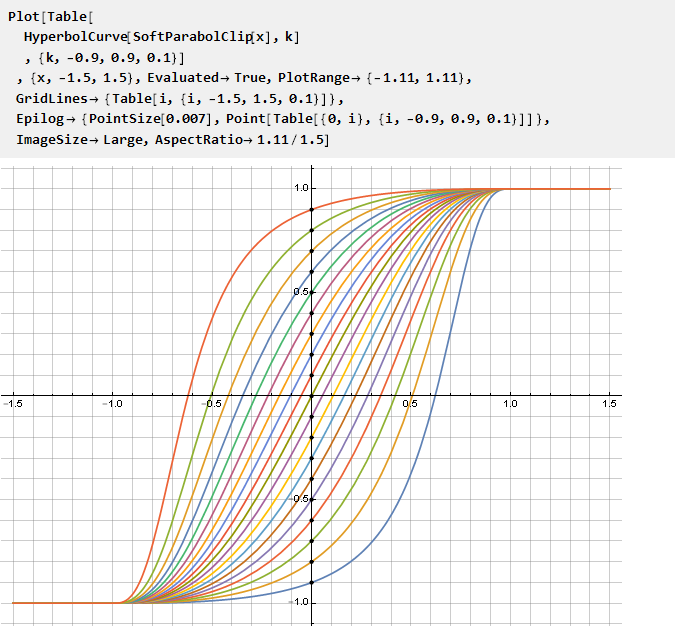
In ähnlicher Weise können Sie Kurven aus anderen Funktionen erstellen, z. B. einem Potenzgesetz mit variabler Basis:
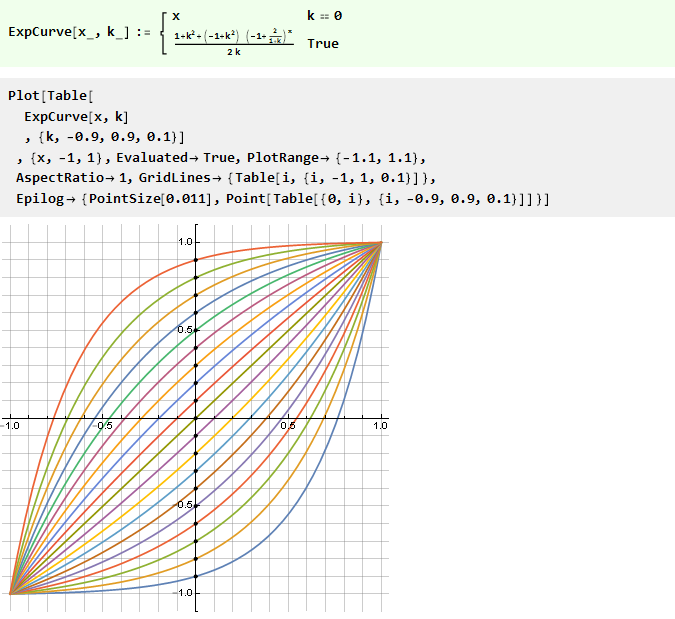
Oder die Umkehrung davon ist logarithmisch:
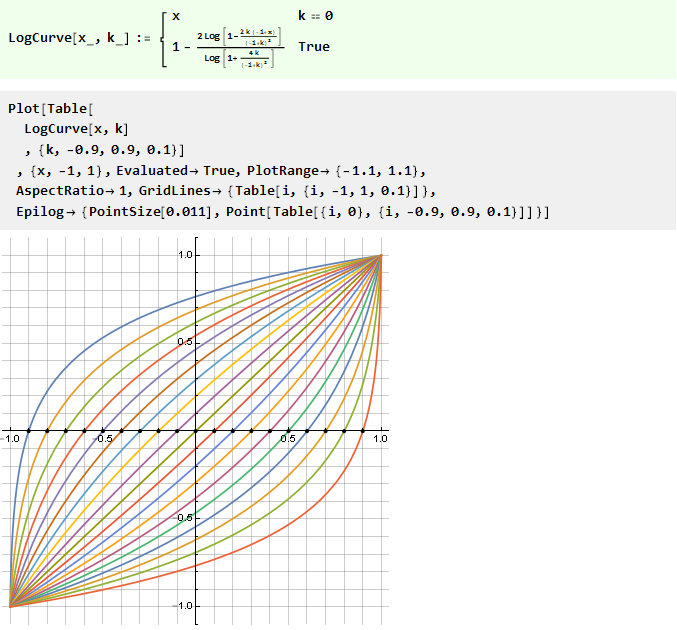
Benötigen Sie mehr Genauigkeit
Möglicherweise möchten wir einen garantierten linearen Abstand für eine Funktion in einem bestimmten Intervall haben. Dies ist logisch zu organisieren, indem eine gerade Linie in eine stückweise stetige Funktion eingefügt wird.
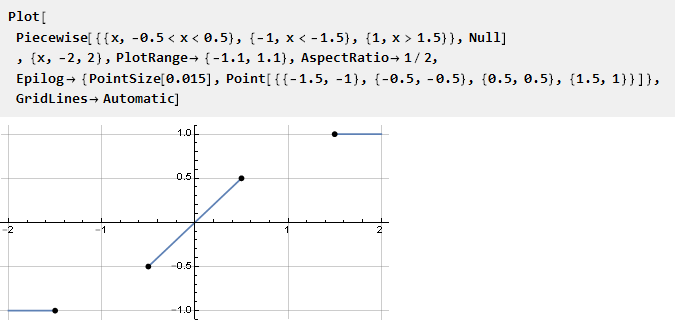
Leerzeichen, in denen Sie eine Funktion ausfüllen müssen. Offensichtlich muss für ein glattes Andocken mit einem linearen Abschnitt seine erste Ableitung gleich Eins sein; und alle nachfolgenden (wenn möglich) Nullen. Um eine solche Funktion nicht neu abzuleiten, können wir eine fertige nehmen und für diese Aufgabe anpassen. Sie können auch feststellen, dass die Extrempunkte etwas weiter als eins liegen - dies ist erforderlich, um die Steigung des linearen Abschnitts aufrechtzuerhalten.
Nehmen Sie die zuvor abgeleitete PolySoft-Funktion und verschieben Sie sie so, dass wir eine in der Mitte der Koordinaten erhalten:
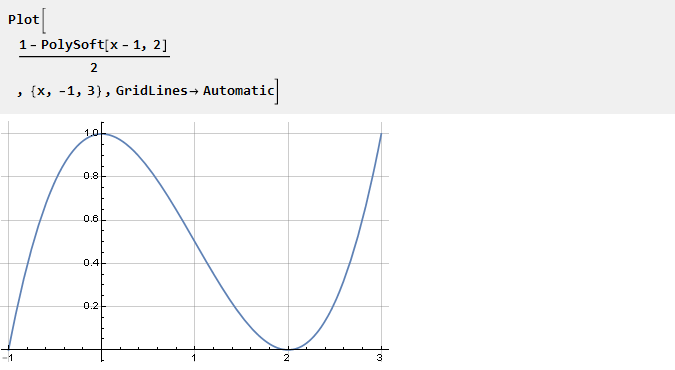
Aus seinen Eigenschaften folgt, dass n-1 der nachfolgenden Ableitungen an den Punkten 0 und 2 gleich Null ist:
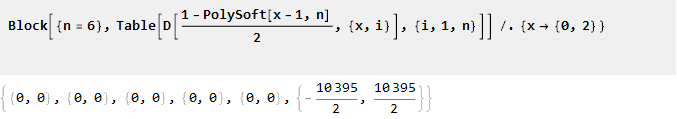
Integrieren Sie es jetzt:
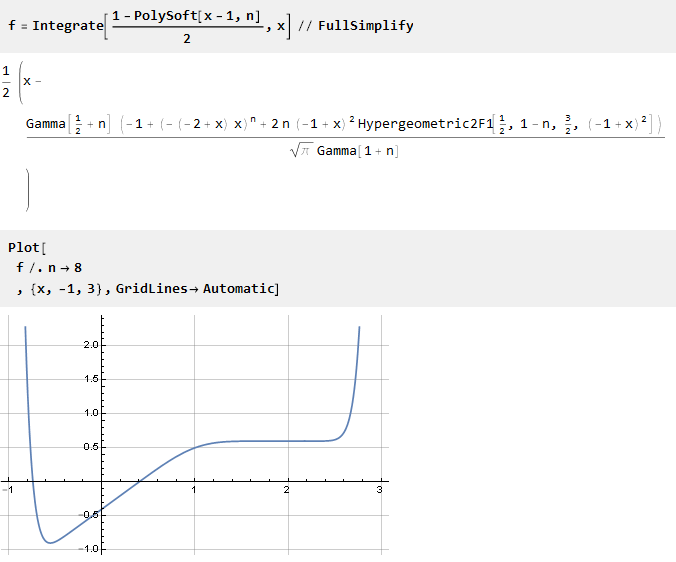
Die Funktion wurde relativ zur Abszissenachse nach unten verschoben. Daher muss eine Konstante (gleich dem Wert der Funktion am Punkt 0) hinzugefügt werden, um die Koordinatenzentren zu kombinieren:

Hier haben wir Null im Grad n. Es hat nicht abgenommen, da der Wert Null im Grad Null nicht definiert ist; wir können es manuell löschen oder vereinfachend explizit angeben, dass n größer als Null ist:

Wir prüfen nur für den Fall. Der Wert an den Punkten 0 und 2 für alle n:

Ableitungen an den Rändern des Intervalls (für ein Polynom der Ordnung 5):

Wie Sie sehen können, erwies sich die Funktion als ziemlich umständlich. Um es nicht zu ziehen und die Berechnungen nicht zu komplizieren, werden wir weiterhin mit einem bestimmten Polynom manipulieren, zum Beispiel 4. Ordnung:

Und jetzt können Sie damit den freien Platz füllen:

Überprüfen Sie:
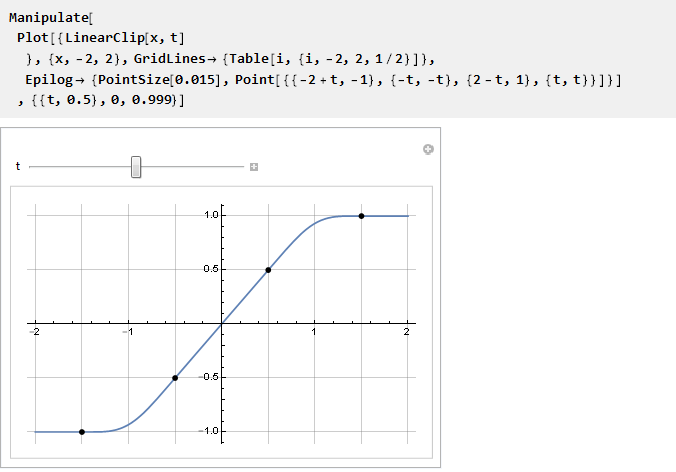
Wir gehen ins Unendliche
Manchmal sind Funktionen erforderlich, die zu einer Einheit tendieren, diese jedoch nicht erreichen. Wikipedia
schlägt mehrere bekannte Lösungen vor:
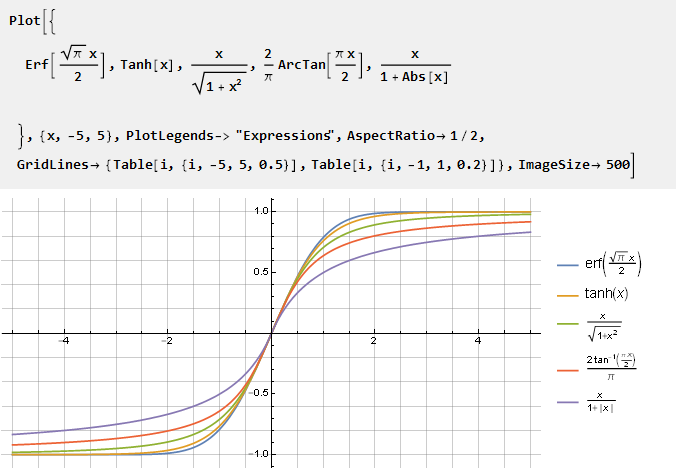
Da diese Funktionen keine Einheit erreichen, ist es bequemer, sie in Bezug auf die Ableitung im Koordinatenzentrum zu normalisieren.
Wir können die Form solcher Funktionen durch ihre Argumentation unter Verwendung einer diagonalsymmetrischen Funktion modifizieren, zum Beispiel:
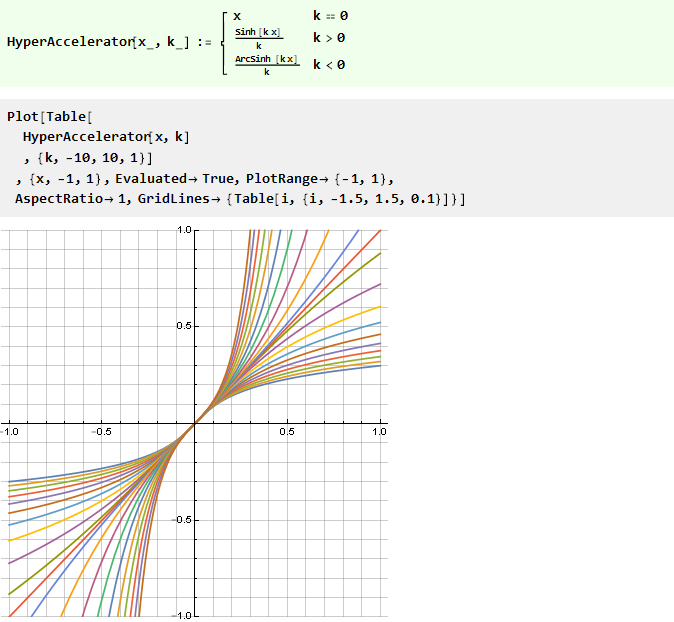
Diese Funktion ist übrigens auch zu sich selbst umgekehrt, d.h.
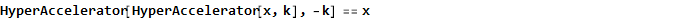
Und als Beispiel für Arkustangens erhalten wir
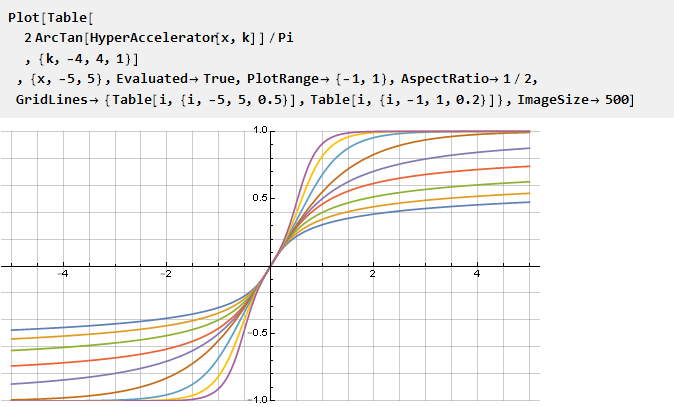
was insbesondere mit dem Parameter k = 1
die Guderman-Funktion ergibt .
Wie Sie sehen können, können mit diesem Ansatz unerwünschte Knicke erhalten werden, daher ist es bevorzugter, die Steifheit der Beschränkung direkt durch die Eigenschaft der Funktion selbst zu steuern. Betrachten Sie mehrere solcher Funktionen mit einem Parameter, dessen Ausgabe der Kürze halber weggelassen wird.
Aus der Power-Funktion:
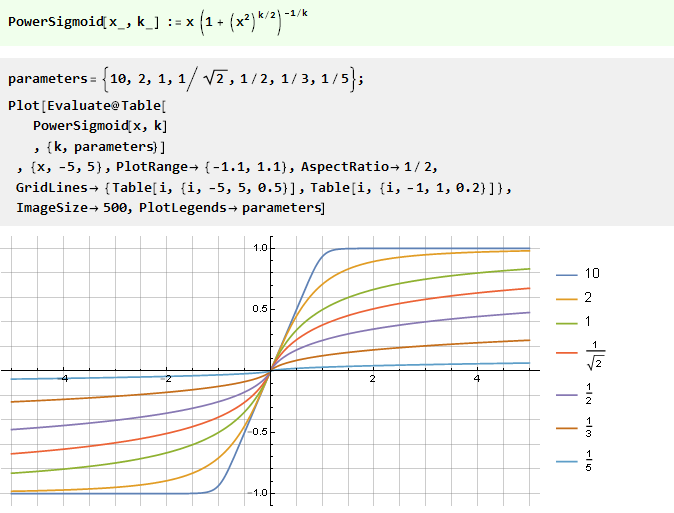
Aus der Summe zweier v-förmiger Funktionen mit Versatz:
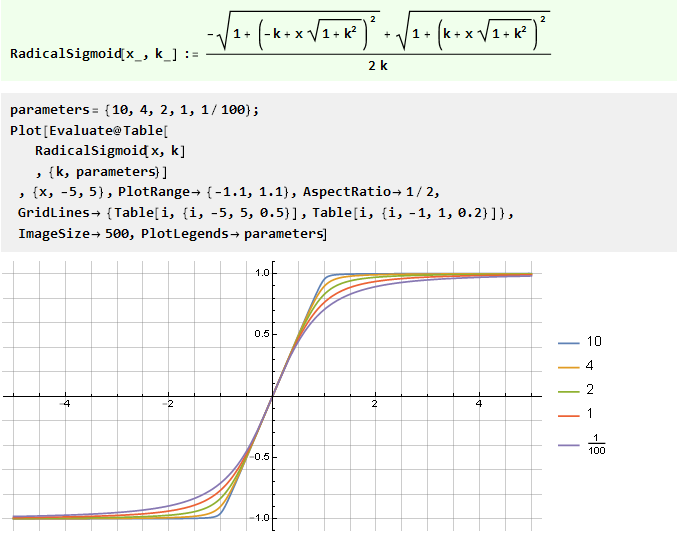
Aus der verallgemeinerten Fehlerfunktion:
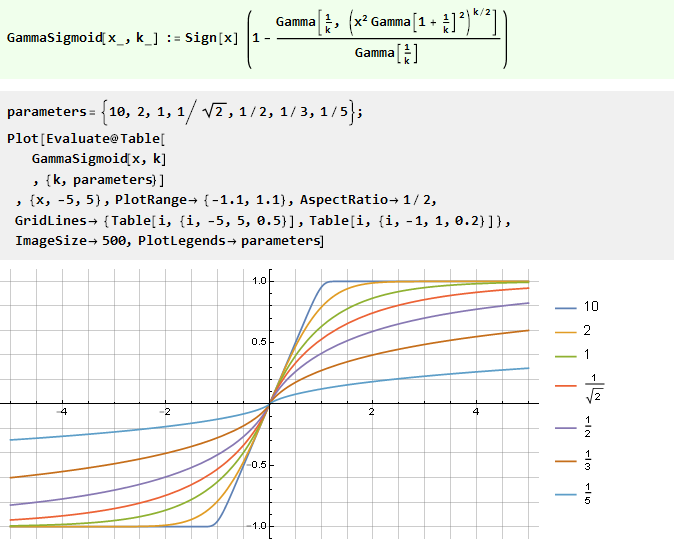
Integration eines rationalen Polynoms:
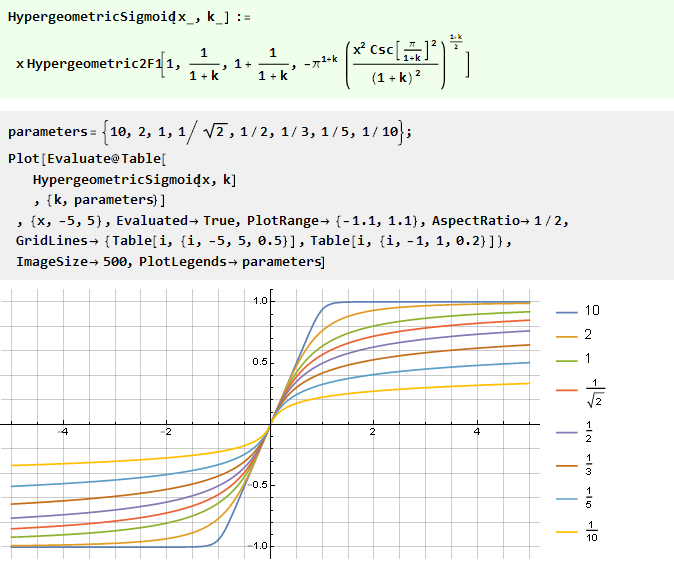
Interessanterweise ist sein Sonderfall arktangent:

Fazit
Die Konstruktion solcher Funktionen kann eine faszinierende Aufgabe sein, bei der sowohl einfache als auch komplexe, sowohl schöne als auch nicht sehr formelhafte Formeln erhalten werden. Es mag den Anschein haben, dass sie sich alle sehr ähnlich sind und eine solche Vielfalt nicht erforderlich ist. Dies ist nicht unbedingt der Fall.
Der Unterschied kann auf anderen Skalen besser sichtbar sein - zum Beispiel logarithmisch. Zusätzlich zu den im Header angegebenen Aufgaben können ähnliche Funktionen für andere Aufgaben verwendet werden - Mischen von Signalen, wenn die gleichmäßige Dämpfung eines Signals mit einer sanften Erhöhung eines anderen kombiniert wird, oder die Konstruktion von akustischen Filtern - und dann wird der Unterschied vom Ohr wahrgenommen oder zum Erstellen von Gradienten - und dann wird der Unterschied vom Auge wahrgenommen. Darüber hinaus können sie auch als Spender für andere, komplexere Funktionen verwendet werden - beispielsweise für
Fenster .
Abschließend ist noch ein paar Punkte zu klären.
Alle Funktionen wurden hier im Bereich von -1 bis 1 definiert. Wenn Sie einen anderen Bereich benötigen (z. B. von 0 bis 1), kann dieser entweder manuell nachgezählt werden:
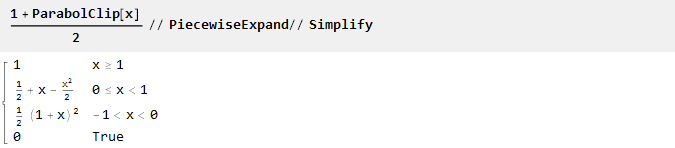
Oder verwenden Sie die integrierte Zoomfunktion:

Um den Export der erhaltenen Formeln in den Programmcode zu erleichtern, kann die CForm-Funktion nützlich sein:
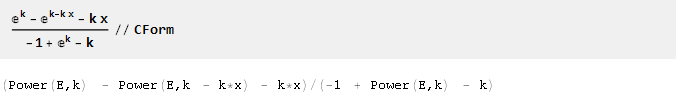
Das Mathematica-Quelldokument kann hier heruntergeladen
werden .
Anmerkungen:
[1] Ein wahrer Mathematiker wird diese Aussage sicherlich rigoros beweisen (oder widerlegen) können.
[2] Hypergeometrische Funktionen werden im Standardkurs der mathematischen Analyse nicht berücksichtigt.
[3] Diese Überladung ist nur für eine Zeicheneinheit definiert. Eine Einheit in einem Gleitkommaformat (z. B. beim Zeichnen eines Diagramms) wird nicht erkannt.