Hallo habr.
Das Thema "magische Quadrate" ist ziemlich interessant, weil Einerseits sind sie seit der Antike bekannt, andererseits ist die Berechnung des "magischen Quadrats" auch heute noch eine sehr schwierige Rechenaufgabe. Denken Sie daran, um das „magische Quadrat“ NxN zu konstruieren, müssen Sie die Zahlen 1..N * N eingeben, damit die Summe seiner Horizontalen, Vertikalen und Diagonalen gleich der gleichen Zahl ist. Wenn Sie einfach die Anzahl aller Optionen zum Anordnen der Zahlen für ein 4x4-Quadrat sortieren, erhalten wir 16! = 20.922.789.888.000 Optionen.
Überlegen Sie, wie dies effizienter durchgeführt werden kann.

Zunächst wiederholen wir den Zustand des Problems. Sie müssen die Zahlen in einem Quadrat anordnen, damit sie sich nicht wiederholen, und die Summe der Horizontalen, Vertikalen und Diagonalen war gleich der gleichen Zahl.
Es ist leicht zu beweisen, dass diese Summe immer gleich ist und nach der Formel für jedes n berechnet wird:
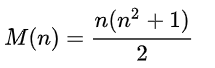
Wir werden 4x4 Quadrate betrachten, also die Summe = 34.
Bezeichne alle Variablen mit X, unser Quadrat sieht folgendermaßen aus:
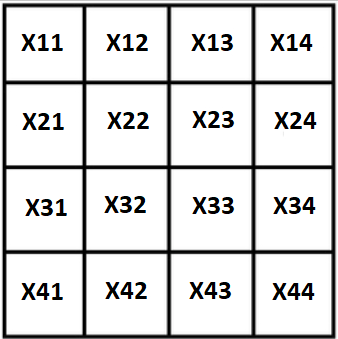
Die erste und offensichtliche Eigenschaft: Wenn die Summe des Quadrats bekannt ist, können die extremen Stoblts durch die verbleibenden 3 ausgedrückt werden:
X14 = S - X11 - X12 - X13
X24 = S - X21 - X22 - X23
...
X41 = S - X11 - X21 - X31So wird aus einem 4x4-Quadrat tatsächlich ein 3x3-Quadrat, wodurch die Anzahl der Suchoptionen von 16 reduziert wird! bis zu 9!, d.h. 57 Millionen Mal. Wenn wir das wissen, beginnen wir Code zu schreiben und sehen, wie kompliziert eine solch erschöpfende Suche nach modernen Computern ist.
C ++ - Single-Threaded-Version
Das Prinzip des Programms ist sehr einfach. Wir nehmen die Menge der Zahlen 1..16 und die for-Schleife über diese Menge, es wird x11 sein. Dann nehmen wir den zweiten Satz, bestehend aus dem ersten mit Ausnahme der Zahl x11 und so weiter.
Eine ungefähre Form des Programms sieht folgendermaßen aus:
int squares = 0; int digits[] = { 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16 }; Set mset(digits, digits + N*N); for (int x11 = 1; x11 <= MAX; x11++) { Set set12(mset); set12.erase(x11); for (SetIterator it12 = set12.begin(); it12 != set12.end(); it12++) { int x12 = *it12; Set set13(set12); set13.erase(x12); for (SetIterator it13 = set13.begin(); it13 != set13.end(); it13++) { int x13 = *it13; int x14 = S - x11 - x12 - x13; if (x14 < 1 || x14 > MAX) continue; if (x14 == x11 || x14 == x12 || x14 == x13) continue; ... int sh1 = x11 + x12 + x13 + x14, sh2 = x21 + x22 + x23 + x24, sh3 = x31 + x32 + x33 + x34, sh4 = x41 + x42 + x43 + x44; int sv1 = x11 + x21 + x31 + x41, sv2 = x12 + x22 + x32 + x42, sv3 = x13 + x23 + x33 + x43, sv4 = x14 + x24 + x34 + x44; int sd1 = x11 + x22 + x33 + x44, sd2 = x14 + x23 + x32 + x41; if (sh1 != S || sh2 != S || sh3 != S || sh4 != S || sv1 != S || sv2 != S || sv3 != S || sv4 != S || sd1 != S || sd2 != S) continue;
Den vollständigen Text des Programms finden Sie unter dem Spoiler.
Ganze Quelle #include <set> #include <stdio.h> #include <ctime> #include "stdafx.h" typedef std::set<int> Set; typedef Set::iterator SetIterator; #define N 4 #define MAX (N*N) #define S 34 int main(int argc, char *argv[]) { // x11 x12 x13 x14 // x21 x22 x23 x24 // x31 x32 x33 x34 // x41 x42 x43 x44 const clock_t begin_time = clock(); int squares = 0; int digits[] = { 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16 }; Set mset(digits, digits + N*N); for (int x11 = 1; x11 <= MAX; x11++) { Set set12(mset); set12.erase(x11); for (SetIterator it12 = set12.begin(); it12 != set12.end(); it12++) { int x12 = *it12; Set set13(set12); set13.erase(x12); for (SetIterator it13 = set13.begin(); it13 != set13.end(); it13++) { int x13 = *it13; int x14 = S - x11 - x12 - x13; if (x14 < 1 || x14 > MAX) continue; if (x14 == x11 || x14 == x12 || x14 == x13) continue; Set set21(set13); set21.erase(x13); set21.erase(x14); for (SetIterator it21 = set21.begin(); it21 != set21.end(); it21++) { int x21 = *it21; Set set22(set21); set22.erase(x21); for (SetIterator it22 = set22.begin(); it22 != set22.end(); it22++) { int x22 = *it22; Set set23(set22); set23.erase(x22); for (SetIterator it23 = set23.begin(); it23 != set23.end(); it23++) { int x23 = *it23, x24 = S - x21 - x22 - x23; if (x24 < 1 || x24 > MAX) continue; if (x24 == x11 || x24 == x12 || x24 == x13 || x24 == x14 || x24 == x21 || x24 == x22 || x24 == x23) continue; Set set31(set23); set31.erase(x23); set31.erase(x24); for (SetIterator it31 = set31.begin(); it31 != set31.end(); it31++) { int x31 = *it31; Set set32(set31); set32.erase(x31); for (SetIterator it32 = set32.begin(); it32 != set32.end(); it32++) { int x32 = *it32; Set set33(set32); set33.erase(x32); for (SetIterator it33 = set33.begin(); it33 != set33.end(); it33++) { int x33 = *it33, x34 = S - x31 - x32 - x33; if (x34 < 1 || x34 > MAX) continue; if (x34 == x11 || x34 == x12 || x34 == x13 || x34 == x14 || x34 == x21 || x34 == x22 || x34 == x23 || x34 == x24 || x34 == x31 || x34 == x32 || x34 == x33) continue; int x41 = S - x11 - x21 - x31, x42 = S - x12 - x22 - x32, x43 = S - x13 - x23 - x33, x44 = S - x14 - x24 - x34; if (x41 < 1 || x41 > MAX || x42 < 1 || x42 > MAX || x43 < 1 || x43 > MAX || x44 < 1 || x41 > MAX) continue; if (x41 == x11 || x41 == x12 || x41 == x13 || x41 == x14 || x41 == x21 || x41 == x22 || x41 == x23 || x41 == x24 || x41 == x31 || x41 == x32 || x41 == x33 || x41 == x34) continue; if (x42 == x11 || x42 == x12 || x42 == x13 || x42 == x14 || x42 == x21 || x42 == x22 || x42 == x23 || x42 == x24 || x42 == x31 || x42 == x32 || x42 == x33 || x42 == x34 || x42 == x41) continue; if (x43 == x11 || x43 == x12 || x43 == x13 || x43 == x14 || x43 == x21 || x43 == x22 || x43 == x23 || x43 == x24 || x43 == x31 || x43 == x32 || x43 == x33 || x43 == x34 || x43 == x41 || x43 == x42) continue; if (x44 == x11 || x44 == x12 || x44 == x13 || x44 == x14 || x44 == x21 || x44 == x22 || x44 == x23 || x44 == x24 || x44 == x31 || x44 == x32 || x44 == x33 || x44 == x34 || x44 == x41 || x44 == x42 || x44 == x43) continue; int sh1 = x11 + x12 + x13 + x14, sh2 = x21 + x22 + x23 + x24, sh3 = x31 + x32 + x33 + x34, sh4 = x41 + x42 + x43 + x44; int sv1 = x11 + x21 + x31 + x41, sv2 = x12 + x22 + x32 + x42, sv3 = x13 + x23 + x33 + x43, sv4 = x14 + x24 + x34 + x44; int sd1 = x11 + x22 + x33 + x44, sd2 = x14 + x23 + x32 + x41; if (sh1 != S || sh2 != S || sh3 != S || sh4 != S || sv1 != S || sv2 != S || sv3 != S || sv4 != S || sd1 != S || sd2 != S) continue; printf("%d %d %d %d %d %d %d %d %d %d %d %d %d %d %d %d\n", x11, x12, x13, x14, x21, x22, x23, x24, x31, x32, x33, x34, x41, x42, x43, x44); squares++; } } } } } } } } } printf("CNT: %d\n", squares); float diff_t = float(clock() - begin_time)/CLOCKS_PER_SEC; printf("T = %.2fs\n", diff_t); return 0; }
Ergebnis: Es wurden insgesamt
7040 4x4-
Optionen für „magische Quadrate“ gefunden, und die Suchzeit betrug
102 Sekunden .

Übrigens ist es interessant zu überprüfen, ob die Liste der Quadrate dieselbe enthält, die auf Dürers Gravur abgebildet ist. Natürlich gibt es, weil Das Programm zeigt
alle 4x4-Quadrate an:
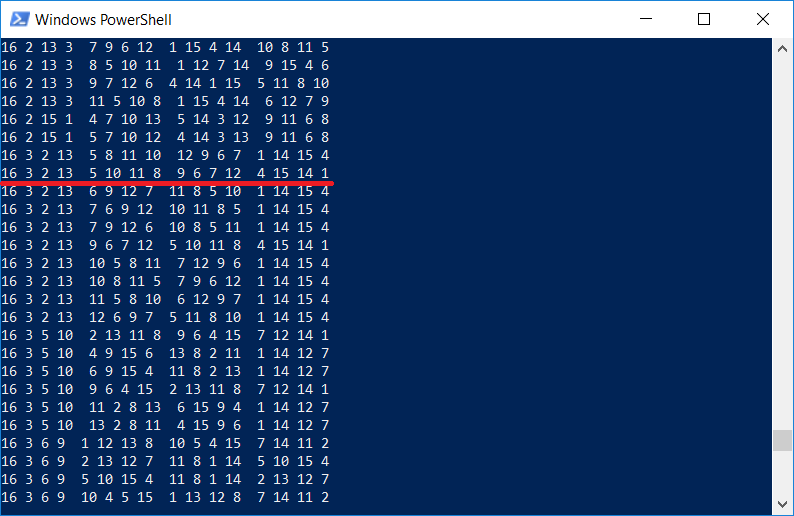
Es sei darauf hingewiesen, dass Dürer aus einem bestimmten Grund ein Quadrat in das Bild eingefügt hat. Die Zahlen
1514 geben auch das Jahr der Gravur an.
Wie Sie sehen können, funktioniert das Programm (wir markieren die Aufgabe als von Albrecht Dürer um 1514 verifiziert;), aber die Ausführungszeit ist für einen Computer mit einem Core i7-Prozessor nicht so gering. Offensichtlich läuft das Programm in einem einzigen Thread, und es ist ratsam, alle anderen Kernel zu verwenden.
C ++ - Multithread-Version
Das Umschreiben eines Programms mithilfe von Streams ist grundsätzlich unkompliziert, wenn auch etwas umständlich. Glücklicherweise gibt es heute eine fast vergessene Option - die Verwendung von Unterstützung für
OpenMP (Open Multi-Processing). Diese Technologie existiert seit 1998 und ermöglicht es Prozessoranweisungen, dem Compiler mitzuteilen, welche Teile des Programms parallel ausgeführt werden sollen. OpenMP wird auch in Visual Studio unterstützt. Um ein Programm in ein Multithread-Programm umzuwandeln, fügen Sie dem Code einfach eine Zeile hinzu:
int squares = 0; #pragma omp parallel for reduction(+: squares) for (int x11 = 1; x11 <= MAX; x11++) { ... } printf("CNT: %d\n", squares);
Die
Direktive #pragma omp parallel for gibt an, dass die nächste for-Schleife parallel ausgeführt werden kann, und die zusätzlichen Parameterquadrate legen den Variablennamen fest, der für parallele Threads üblich ist (ohne dies funktioniert das Inkrement nicht richtig).
Das Ergebnis ist offensichtlich: Die Ausführungszeit wurde von 102 auf
18 Sekunden reduziert.

Ganze Quelle #include <set> #include <stdio.h> #include <ctime> #include "stdafx.h" typedef std::set<int> Set; typedef Set::iterator SetIterator; #define N 4 #define MAX (N*N) #define S 34 int main(int argc, char *argv[]) { // x11 x12 x13 x14 // x21 x22 x23 x24 // x31 x32 x33 x34 // x41 x42 x43 x44 const clock_t begin_time = clock(); int squares = 0; #pragma omp parallel for reduction(+: squares) for (int x11 = 1; x11 <= MAX; x11++) { int digits[] = { 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16 }; Set mset(digits, digits + N*N); Set set12(mset); set12.erase(x11); for (SetIterator it12 = set12.begin(); it12 != set12.end(); it12++) { int x12 = *it12; Set set13(set12); set13.erase(x12); for (SetIterator it13 = set13.begin(); it13 != set13.end(); it13++) { int x13 = *it13; int x14 = S - x11 - x12 - x13; if (x14 < 1 || x14 > MAX) continue; if (x14 == x11 || x14 == x12 || x14 == x13) continue; Set set21(set13); set21.erase(x13); set21.erase(x14); for (SetIterator it21 = set21.begin(); it21 != set21.end(); it21++) { int x21 = *it21; Set set22(set21); set22.erase(x21); for (SetIterator it22 = set22.begin(); it22 != set22.end(); it22++) { int x22 = *it22; Set set23(set22); set23.erase(x22); for (SetIterator it23 = set23.begin(); it23 != set23.end(); it23++) { int x23 = *it23, x24 = S - x21 - x22 - x23; if (x24 < 1 || x24 > MAX) continue; if (x24 == x11 || x24 == x12 || x24 == x13 || x24 == x14 || x24 == x21 || x24 == x22 || x24 == x23) continue; Set set31(set23); set31.erase(x23); set31.erase(x24); for (SetIterator it31 = set31.begin(); it31 != set31.end(); it31++) { int x31 = *it31; Set set32(set31); set32.erase(x31); for (SetIterator it32 = set32.begin(); it32 != set32.end(); it32++) { int x32 = *it32; Set set33(set32); set33.erase(x32); for (SetIterator it33 = set33.begin(); it33 != set33.end(); it33++) { int x33 = *it33, x34 = S - x31 - x32 - x33; if (x34 < 1 || x34 > MAX) continue; if (x34 == x11 || x34 == x12 || x34 == x13 || x34 == x14 || x34 == x21 || x34 == x22 || x34 == x23 || x34 == x24 || x34 == x31 || x34 == x32 || x34 == x33) continue; int x41 = S - x11 - x21 - x31, x42 = S - x12 - x22 - x32, x43 = S - x13 - x23 - x33, x44 = S - x14 - x24 - x34; if (x41 < 1 || x41 > MAX || x42 < 1 || x42 > MAX || x43 < 1 || x43 > MAX || x44 < 1 || x41 > MAX) continue; if (x41 == x11 || x41 == x12 || x41 == x13 || x41 == x14 || x41 == x21 || x41 == x22 || x41 == x23 || x41 == x24 || x41 == x31 || x41 == x32 || x41 == x33 || x41 == x34) continue; if (x42 == x11 || x42 == x12 || x42 == x13 || x42 == x14 || x42 == x21 || x42 == x22 || x42 == x23 || x42 == x24 || x42 == x31 || x42 == x32 || x42 == x33 || x42 == x34 || x42 == x41) continue; if (x43 == x11 || x43 == x12 || x43 == x13 || x43 == x14 || x43 == x21 || x43 == x22 || x43 == x23 || x43 == x24 || x43 == x31 || x43 == x32 || x43 == x33 || x43 == x34 || x43 == x41 || x43 == x42) continue; if (x44 == x11 || x44 == x12 || x44 == x13 || x44 == x14 || x44 == x21 || x44 == x22 || x44 == x23 || x44 == x24 || x44 == x31 || x44 == x32 || x44 == x33 || x44 == x34 || x44 == x41 || x44 == x42 || x44 == x43) continue; int sh1 = x11 + x12 + x13 + x14, sh2 = x21 + x22 + x23 + x24, sh3 = x31 + x32 + x33 + x34, sh4 = x41 + x42 + x43 + x44; int sv1 = x11 + x21 + x31 + x41, sv2 = x12 + x22 + x32 + x42, sv3 = x13 + x23 + x33 + x43, sv4 = x14 + x24 + x34 + x44; int sd1 = x11 + x22 + x33 + x44, sd2 = x14 + x23 + x32 + x41; if (sh1 != S || sh2 != S || sh3 != S || sh4 != S || sv1 != S || sv2 != S || sv3 != S || sv4 != S || sd1 != S || sd2 != S) continue; printf("%d %d %d %d %d %d %d %d %d %d %d %d %d %d %d %d\n", x11, x12, x13, x14, x21, x22, x23, x24, x31, x32, x33, x34, x41, x42, x43, x44); squares++; } } } } } } } } } printf("CNT: %d\n", squares); float diff_t = float(clock() - begin_time)/CLOCKS_PER_SEC; printf("T = %.2fs\n", diff_t); return 0; }
Das ist viel besser - weil Die Aufgabe ist nahezu perfekt parallelisiert (die Berechnungen in jedem Zweig sind unabhängig voneinander). Die Zeit ist kürzer als die Anzahl der Prozessorkerne. Leider ist es nicht möglich, viel mehr aus diesem Code herauszuholen, obwohl einige Prozent durch einige Optimierungen gewonnen werden können und können. Wir gehen zu schwererer Artillerie über, Berechnungen auf der GPU.
Rechnen mit NVIDIA CUDA
Wenn Sie nicht auf Details eingehen, kann der auf der Grafikkarte ausgeführte Berechnungsprozess als mehrere parallele Hardwareblöcke (Blöcke) dargestellt werden, von denen jeder mehrere Prozesse (Threads) ausführt.
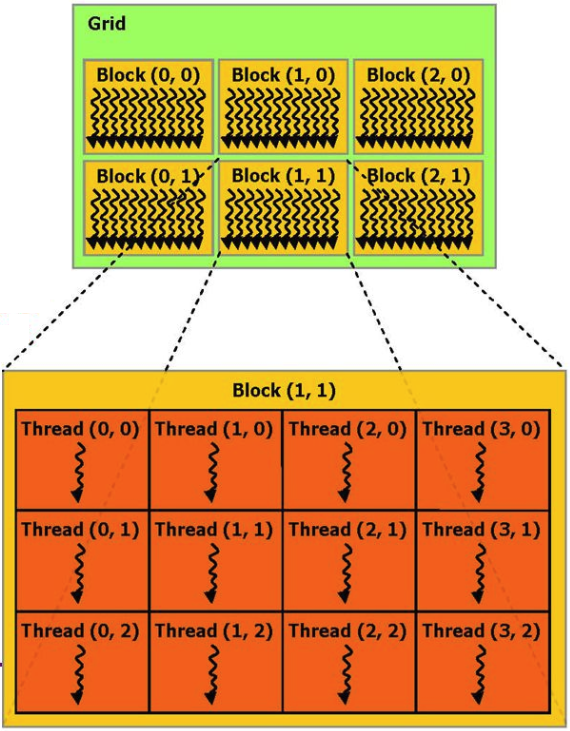
Zum Beispiel können wir ein Beispiel für die Funktion des Hinzufügens von 2 Vektoren aus der CUDA-Dokumentation geben:
__global__ void add(int n, float *x, float *y) { int index = threadIdx.x; int stride = blockDim.x; for (int i = index; i < n; i += stride) y[i] = x[i] + y[i]; }
Die Arrays x und y sind allen Blöcken gemeinsam, und die Funktion selbst wird somit gleichzeitig auf mehreren Prozessoren ausgeführt. Der Schlüssel liegt hier in der Parallelität - Grafikkartenprozessoren sind viel einfacher als eine normale CPU, aber es gibt viele davon, und sie konzentrieren sich speziell auf die Verarbeitung numerischer Daten.
Das brauchen wir. Wir haben eine Matrix von Zahlen X11, X12, .., X44. Beginnen wir mit 16 Blöcken, von denen jeder 16 Prozesse ausführt. Die Blocknummer entspricht der Nummer X11, die Prozessnummer der Nummer X12 und der Code selbst berechnet alle möglichen Quadrate mit für die ausgewählten X11 und X12. Es ist einfach, aber es gibt eine Subtilität: Die Daten müssen nicht nur berechnet, sondern auch von der Grafikkarte zurück übertragen werden. Dazu speichern wir die Anzahl der Quadrate, die im Nullelement des Arrays gefunden werden.
Der Hauptcode ist sehr einfach:
#define N 4 #define SQ_MAX 8*1024 #define BLOCK_SIZE (SQ_MAX*N*N + 1) int main(int argc,char *argv[]) { const clock_t begin_time = clock(); int *results = (int*)malloc(BLOCK_SIZE*sizeof(int)); results[0] = 0; int *gpu_out = NULL; cudaMalloc(&gpu_out, BLOCK_SIZE*sizeof(int)); cudaMemcpy(gpu_out, results, BLOCK_SIZE*sizeof(int), cudaMemcpyHostToDevice); squares<<<MAX, MAX>>>(gpu_out); cudaMemcpy(results, gpu_out, BLOCK_SIZE*sizeof(int), cudaMemcpyDeviceToHost); // Print results int squares = results[0]; for(int p=0; p<SQ_MAX && p<squares; p++) { int i = MAX*p + 1; printf("[%d %d %d %d %d %d %d %d %d %d %d %d %d %d %d %d]\n", results[i], results[i+1], results[i+2], results[i+3], results[i+4], results[i+5], results[i+6], results[i+7], results[i+8], results[i+9], results[i+10], results[i+11], results[i+12], results[i+13], results[i+14], results[i+15]); } printf ("CNT: %d\n", squares); float diff_t = float(clock() - begin_time)/CLOCKS_PER_SEC; printf("T = %.2fs\n", diff_t); cudaFree(gpu_out); free(results); return 0; }
Wir wählen den Speicherblock auf der Grafikkarte mit cudaMalloc aus, führen die Quadratfunktion aus und geben 2 Parameter 16.16 (Anzahl der Blöcke und Anzahl der Threads) an, die den sortierten Nummern 1..16 entsprechen, und kopieren dann die Daten über cudaMemcpy zurück.
Die Quadratsfunktion selbst wiederholt im Wesentlichen den Code aus dem vorherigen Teil, mit dem Unterschied, dass das Inkrementieren der Anzahl der gefundenen Quadrate mit atomicAdd erfolgt - dies stellt sicher, dass sich die Variable bei gleichzeitigen Aufrufen korrekt ändert.
Das Ergebnis erfordert keine Kommentare - die Ausführungszeit betrug
2,7 s , was etwa 30-mal besser ist als die ursprüngliche Single-Threaded-Version:

Wie in den Kommentaren vorgeschlagen, können Sie noch mehr Hardwareblöcke der Grafikkarte verwenden, sodass die Option von 256 Blöcken ausprobiert wurde. Das Ändern des Codes ist minimal:
__global__ void squares(int *res_array) { int index1 = blockIdx.x/MAX, index2 = blockIdx.x%MAX; ... } squares<<<MAX*MAX, 1>>>(gpu_out);
Dies reduzierte die Zeit um weitere 2 Mal auf
1,2 Sekunden . Ferner können auf jedem Block 16 Prozesse gestartet werden, was die beste Zeit von
0,44 s ergibt .
Endgültiger Code #include <stdio.h> #include <ctime> #define N 4 #define MAX (N*N) #define SQ_MAX 8*1024 #define BLOCK_SIZE (SQ_MAX*N*N + 1) #define S 34 // Magic square: // x11 x12 x13 x14 // x21 x22 x23 x24 // x31 x32 x33 x34 // x41 x42 x43 x44 __global__ void squares(int *res_array) { int index1 = blockIdx.x/MAX, index2 = blockIdx.x%MAX, index3 = threadIdx.x; if (index1 + 1 > MAX || index2 + 1 > MAX || index3 + 1 > MAX) return; const int x11 = index1+1, x12 = index2+1, x13 = index3+1; if (x13 == x11 || x13 == x12) return; int x14 = S - x11 - x12 - x13; if (x14 < 1 || x14 > MAX) return; if (x14 == x11 || x14 == x12 || x14 == x13) return; for(int x21=1; x21<=MAX; x21++) { if (x21 == x11 || x21 == x12 || x21 == x13 || x21 == x14) continue; for(int x22=1; x22<=MAX; x22++) { if (x22 == x11 || x22 == x12 || x22 == x13 || x22 == x14 || x22 == x21) continue; for(int x23=1; x23<=MAX; x23++) { int x24 = S - x21 - x22 - x23; if (x24 < 1 || x24 > MAX) continue; if (x23 == x11 || x23 == x12 || x23 == x13 || x23 == x14 || x23 == x21 || x23 == x22) continue; if (x24 == x11 || x24 == x12 || x24 == x13 || x24 == x14 || x24 == x21 || x24 == x22 || x24 == x23) continue; for(int x31=1; x31<=MAX; x31++) { if (x31 == x11 || x31 == x12 || x31 == x13 || x31 == x14 || x31 == x21 || x31 == x22 || x31 == x23 || x31 == x24) continue; for(int x32=1; x32<=MAX; x32++) { if (x32 == x11 || x32 == x12 || x32 == x13 || x32 == x14 || x32 == x21 || x32 == x22 || x32 == x23 || x32 == x24 || x32 == x31) continue; for(int x33=1; x33<=MAX; x33++) { int x34 = S - x31 - x32 - x33; if (x34 < 1 || x34 > MAX) continue; if (x33 == x11 || x33 == x12 || x33 == x13 || x33 == x14 || x33 == x21 || x33 == x22 || x33 == x23 || x33 == x24 || x33 == x31 || x33 == x32) continue; if (x34 == x11 || x34 == x12 || x34 == x13 || x34 == x14 || x34 == x21 || x34 == x22 || x34 == x23 || x34 == x24 || x34 == x31 || x34 == x32 || x34 == x33) continue; const int x41 = S - x11 - x21 - x31, x42 = S - x12 - x22 - x32, x43 = S - x13 - x23 - x33, x44 = S - x14 - x24 - x34; if (x41 < 1 || x41 > MAX || x42 < 1 || x42 > MAX || x43 < 1 || x43 > MAX || x44 < 1 || x44 > MAX) continue; if (x41 == x11 || x41 == x12 || x41 == x13 || x41 == x14 || x41 == x21 || x41 == x22 || x41 == x23 || x41 == x24 || x41 == x31 || x41 == x32 || x41 == x33 || x41 == x34) continue; if (x42 == x11 || x42 == x12 || x42 == x13 || x42 == x14 || x42 == x21 || x42 == x22 || x42 == x23 || x42 == x24 || x42 == x31 || x42 == x32 || x42 == x33 || x42 == x34 || x42 == x41) continue; if (x43 == x11 || x43 == x12 || x43 == x13 || x43 == x14 || x43 == x21 || x43 == x22 || x43 == x23 || x43 == x24 || x43 == x31 || x43 == x32 || x43 == x33 || x43 == x34 || x43 == x41 || x43 == x42) continue; if (x44 == x11 || x44 == x12 || x44 == x13 || x44 == x14 || x44 == x21 || x44 == x22 || x44 == x23 || x44 == x24 || x44 == x31 || x44 == x32 || x44 == x33 || x44 == x34 || x44 == x41 || x44 == x42 || x44 == x43) continue; int sh1 = x11 + x12 + x13 + x14, sh2 = x21 + x22 + x23 + x24, sh3 = x31 + x32 + x33 + x34, sh4 = x41 + x42 + x43 + x44; int sv1 = x11 + x21 + x31 + x41, sv2 = x12 + x22 + x32 + x42, sv3 = x13 + x23 + x33 + x43, sv4 = x14 + x24 + x34 + x44; int sd1 = x11 + x22 + x33 + x44, sd2 = x14 + x23 + x32 + x41; if (sh1 != S || sh2 != S || sh3 != S || sh4 != S || sv1 != S || sv2 != S || sv3 != S || sv4 != S || sd1 != S || sd2 != S) continue; // Square found: save in array (MAX numbers for each square) int p = atomicAdd(res_array, 1); if (p >= SQ_MAX) continue; int i = MAX*p + 1; res_array[i] = x11; res_array[i+1] = x12; res_array[i+2] = x13; res_array[i+3] = x14; res_array[i+4] = x21; res_array[i+5] = x22; res_array[i+6] = x23; res_array[i+7] = x24; res_array[i+8] = x31; res_array[i+9] = x32; res_array[i+10] = x33; res_array[i+11] = x34; res_array[i+12]= x41; res_array[i+13]= x42; res_array[i+14] = x43; res_array[i+15] = x44; // Warning: printf from kernel makes calculation 2-3x slower // printf("%d %d %d %d %d %d %d %d %d %d %d %d %d %d %d %d\n", x11, x12, x13, x14, x21, x22, x23, x24, x31, x32, x33, x34, x41, x42, x43, x44); } } } } } } } int main(int argc,char *argv[]) { int *gpu_out = NULL; cudaMalloc(&gpu_out, BLOCK_SIZE*sizeof(int)); const clock_t begin_time = clock(); int *results = (int*)malloc(BLOCK_SIZE*sizeof(int)); results[0] = 0; cudaMemcpy(gpu_out, results, BLOCK_SIZE*sizeof(int), cudaMemcpyHostToDevice); squares<<<MAX*MAX, MAX>>>(gpu_out); cudaMemcpy(results, gpu_out, BLOCK_SIZE*sizeof(int), cudaMemcpyDeviceToHost); // Print results int squares = results[0]; for(int p=0; p<SQ_MAX && p<squares; p++) { int i = MAX*p + 1; printf("[%d %d %d %d %d %d %d %d %d %d %d %d %d %d %d %d]\n", results[i], results[i+1], results[i+2], results[i+3], results[i+4], results[i+5], results[i+6], results[i+7], results[i+8], results[i+9], results[i+10], results[i+11], results[i+12], results[i+13], results[i+14], results[i+15]); } printf ("CNT: %d\n", squares); float diff_t = float(clock() - begin_time)/CLOCKS_PER_SEC; printf("T = %.2fs\n", diff_t); cudaFree(gpu_out); free(results); return 0; }
Dies ist höchstwahrscheinlich alles andere als ideal. Sie können beispielsweise noch mehr Blöcke auf der GPU ausführen, dies macht den Code jedoch verwirrender und schwieriger zu verstehen. Und natürlich sind die Berechnungen nicht „kostenlos“ - wenn die GPU geladen ist, verlangsamt sich die Windows-Oberfläche merklich und der Stromverbrauch des Computers steigt fast zweimal von 65 auf 130 W.
Bearbeiten : Wie der
Bodigrim- Benutzer in den Kommentaren aufgefordert hat, gilt eine andere Gleichheit für das 4x4-Quadrat: Die Summe von 4 "internen" Zellen ist gleich der Summe von "externen" Zellen, es ist auch S.

X22 + X23 + X32 + X33 = X11 + X41 + X14 + X44 = SDies ermöglicht es, den Algorithmus zu beschleunigen, indem einige Variablen durch andere ausgedrückt und weitere 1-2 verschachtelte Schleifen entfernt werden. Eine aktualisierte Version des Codes finden Sie im Kommentar unten.Fazit
Die Aufgabe, „magische Quadrate“ zu finden, erwies sich als technisch sehr interessant und gleichzeitig schwierig. Selbst bei Berechnungen auf der GPU kann die Suche nach allen 5x5-Quadraten mehrere Stunden dauern, und die Optimierung zum Auffinden magischer Quadrate mit 7x7 und höheren Dimensionen muss noch durchgeführt werden.Mathematisch und algorithmisch gibt es auch einige ungelöste Probleme:- « » N. 22 , 33 8 ( 1, ), 44 , 7040, . .
- , .
- . , NVIDIA Tesla , - , . , . , ;)
Bei Interesse kann ein separater Artikel über die Analyse und die Eigenschaften der magischen Quadrate selbst geschrieben werden.PS: Auf die Frage, die wahrscheinlich folgen wird: "Warum ist das notwendig?" In Bezug auf den Stromverbrauch ist die Berechnung von magischen Quadraten nicht besser oder schlechter als die Berechnung von Bitcoins. Warum also nicht? Darüber hinaus ist es ein interessantes Training für den Geist und eine interessante Aufgabe im Bereich der angewandten Programmierung.