MIT-Kurs "Computer Systems Security". Vorlesung 10: Symbolische Ausführung, Teil 3

Massachusetts Institute of Technology. Vorlesung # 6.858. "Sicherheit von Computersystemen." Nikolai Zeldovich, James Mickens. 2014 Jahr

Computer Systems Security ist ein Kurs zur Entwicklung und Implementierung sicherer Computersysteme. Die Vorträge behandeln Bedrohungsmodelle, Angriffe, die die Sicherheit gefährden, und Sicherheitstechniken, die auf jüngsten wissenschaftlichen Arbeiten basieren. Zu den Themen gehören Betriebssystemsicherheit, Funktionen, Informationsflussmanagement, Sprachsicherheit, Netzwerkprotokolle, Hardwaresicherheit und Sicherheit von Webanwendungen.

Vorlesung 1: „Einführung: Bedrohungsmodelle“ Teil 1 / Teil 2 / Teil 3
Vorlesung 2: „Kontrolle von Hackerangriffen“ Teil 1 / Teil 2 / Teil 3
Vorlesung 3: „Pufferüberläufe: Exploits und Schutz“ Teil 1 / Teil 2 / Teil 3
Vorlesung 4: „Trennung von Privilegien“ Teil 1 / Teil 2 / Teil 3
Vorlesung 5: „Woher kommen Sicherheitssysteme?“ Teil 1 / Teil 2
Vorlesung 6: „Chancen“ Teil 1 / Teil 2 / Teil 3
Vorlesung 7: „Native Client Sandbox“ Teil 1 / Teil 2 / Teil 3
Vorlesung 8: „Netzwerksicherheitsmodell“ Teil 1 / Teil 2 / Teil 3
Vorlesung 9: „Sicherheit von Webanwendungen“ Teil 1 / Teil 2 / Teil 3
Vorlesung 10: „Symbolische Ausführung“ Teil 1 / Teil 2 / Teil 3

Wenn wir nun dem Zweig nach unten folgen, sehen wir den Ausdruck t = y. Da wir jeweils einen Pfad betrachten, müssen wir für t keine neue Variable einführen. Wir können einfach sagen, dass t nicht mehr 0 ist, da t = y ist.

Wir bewegen uns weiter nach unten und kommen zu dem Punkt, an dem wir zu einem anderen Zweig gelangen. Was ist die neue Annahme, die wir treffen müssen, um diesen Weg weiter zu beschreiten? Dies ist eine Annahme, dass t <y ist.

Was ist t? Wenn Sie den rechten Zweig nachschlagen, sehen wir, dass t = y ist. Und in unserer Tabelle ist T = y und Y = y. Daraus folgt logischerweise, dass unsere Einschränkung wie y <y aussieht, was nicht sein kann.



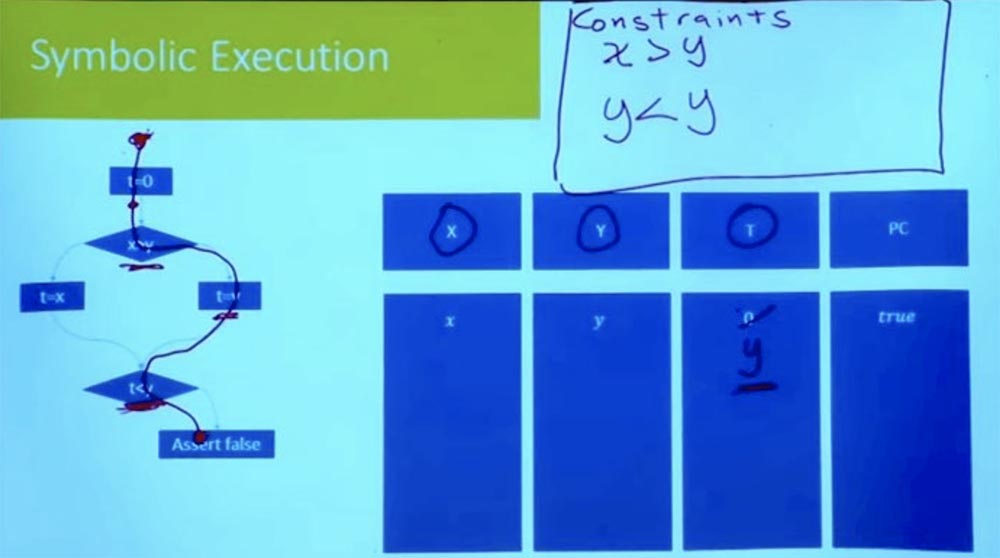
Somit hatten wir alles in Ordnung, bis wir diesen Punkt t <y erreichten. Bis wir zu der falschen Aussage kommen, haben wir alle Ungleichungen, um richtig zu sein. Dies funktioniert jedoch nicht, da bei der Ausführung von Aufgaben des richtigen Zweigs eine logische Inkonsistenz auftritt.

Wir haben das, was oft als Zustand des Pfades bezeichnet wird. Diese Bedingung muss erfüllt sein, damit das Programm diesen Weg einschlägt. Wir wissen jedoch, dass diese Bedingung nicht erfüllt werden kann, daher ist es für das Programm unmöglich, diesen Weg zu gehen. Dieser Weg wurde nun vollständig beseitigt, und wir wissen, dass dieser richtige Weg nicht zurückgelegt werden kann.

Was ist mit dem anderen Weg? Versuchen wir, den linken Zweig auf andere Weise zu durchlaufen. Was sind die Bedingungen für diesen Weg? Wieder beginnt unser symbolischer Zustand bei t = 0 und X und Y sind gleich den Variablen x und y.



Wie sieht die Pfadbeschränkung in diesem Fall jetzt aus? Wir bezeichnen den linken Zweig als True und den rechten Zweig als False und betrachten weiter den Wert t = x. Als Ergebnis der logischen Verarbeitung der Bedingungen t = x, x> y und t <y erhalten wir, dass wir gleichzeitig x> y und x <y haben.



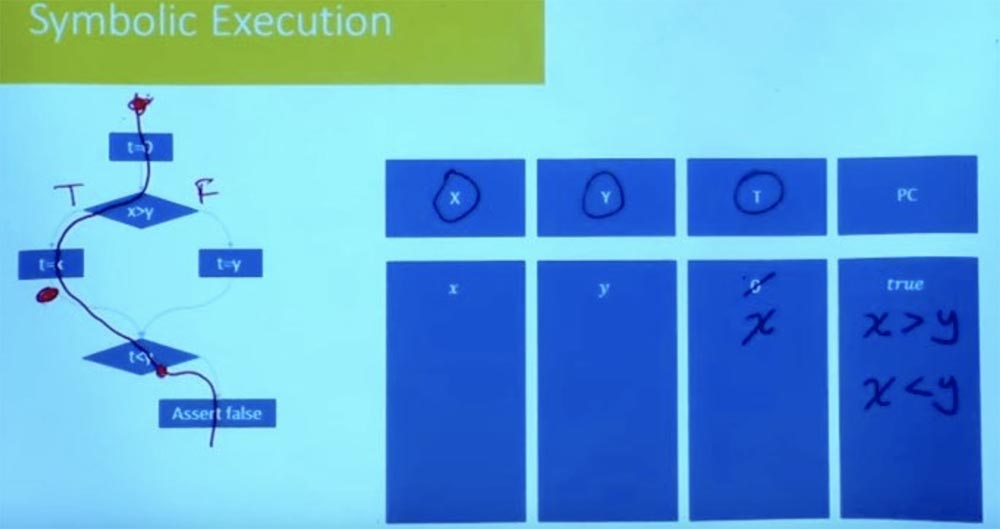
Es ist klar, dass dieser Zustand des Pfades unbefriedigend ist. Wir können kein x haben, das sowohl größer als auch kleiner als y ist. Es gibt keine Zuordnung zu einer Variablen X, die beide Bedingungen erfüllt. Dies zeigt uns also, dass der andere Weg ebenfalls unbefriedigend ist.

Es stellt sich heraus, dass wir in diesem Moment alle möglichen Wege im Programm erkundet haben, die uns in diesen Zustand führen könnten. Wir können tatsächlich feststellen und überprüfen, dass es keinen Weg gibt, der uns zu der Aussage false führen würde.
Zielgruppe: In diesem Beispiel haben Sie gezeigt, dass Sie den Fortschritt eines Programms in allen möglichen Branchen untersucht haben. Einer der Vorteile der symbolischen Ausführung besteht jedoch darin, dass wir nicht alle möglichen exponentiellen Pfade untersuchen müssen. Wie kann man dies in diesem Beispiel vermeiden?

Professor: Das ist eine sehr gute Frage. In diesem Fall gehen Sie einen Kompromiss zwischen der Zeichenausführung und der gewünschten Genauigkeit ein. In diesem Fall verwenden wir weniger die symbolische Ausführung als vielmehr das erste Mal, dass wir den Programmablauf in beiden Zweigen gleichzeitig betrachten. Aber dank dessen sind unsere Einschränkungen sehr, sehr einfach geworden.

Die einzelnen Einschränkungen „auf eine Weise nach der anderen“ sind sehr einfach, aber Sie müssen dies immer wieder tun, indem Sie alle vorhandenen Zweige und exponentiell - und alle möglichen Wege - studieren.
Es gibt exponentiell viele Pfade, aber für jeden Pfad als Ganzes gibt es auch einen exponentiell großen Satz von Eingabedaten, die diesen Pfad gehen können. Dies gibt Ihnen also bereits einen großen Vorteil, denn anstatt alle möglichen Eingaben zu versuchen, versuchen Sie, jeden möglichen Weg zu versuchen. Aber kannst du etwas besser machen?

Dies ist einer der Bereiche, in denen viel experimentiert wurde, beispielsweise in Bezug auf die symbolische Ausführung, beispielsweise die gleichzeitige Ausführung mehrerer Pfade. In den Vorlesungsmaterialien haben Sie Heuristiken und eine Reihe von Strategien kennengelernt, mit denen Experimentatoren die Suche lösbarer gemacht haben.

Zum Beispiel ist eines der Dinge, die sie tun, dass sie einen Weg nach dem anderen erkunden, dies aber nicht völlig blind tun. Sie überprüfen die Bedingungen des Pfades nach jedem Schritt. Angenommen, hier in unserem Programm gibt es anstelle von „false“ einen komplexen Programmbaum, ein Kontrollflussdiagramm.



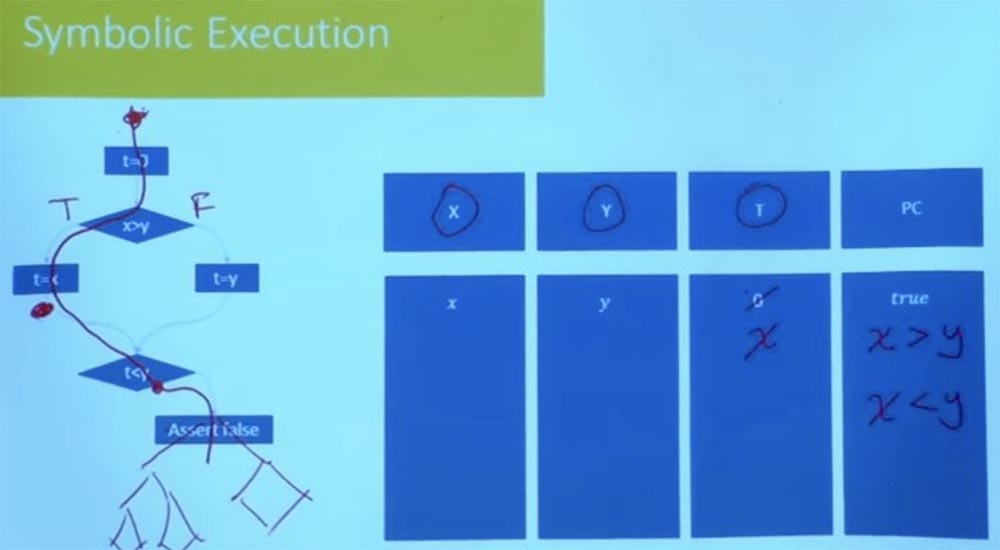
Sie müssen nicht warten, bis Sie das Ende erreicht haben, um zu überprüfen, ob dieser Pfad möglich ist. In diesem Moment, wenn Sie die Bedingung t <y erreichen, wissen Sie bereits, dass dieser Weg unbefriedigend ist, und Sie werden niemals in diese Richtung gehen. Das Abschneiden der falschen Zweige zu Beginn des Programms reduziert daher den Aufwand für empirische Arbeiten. Eine angemessene Erkundung des Pfades verhindert die Möglichkeit eines zukünftigen Programmfehlers. Viele der praktischen Werkzeuge, die heute verwendet werden, beginnen hauptsächlich mit zufälligen Tests, um die ersten Pfade zu erhalten. Danach beginnen sie, die Pfade in der Nachbarschaft zu erkunden. Sie verarbeiten viele Optionen für die mögliche Ausführung des Programms für jeden Zweig und fragen sich, was auf diesen Pfaden passiert.

Es ist besonders nützlich, wenn wir eine gute Reihe von Tests haben. Sie führen Ihren Test aus und stellen fest, dass dieser Code nicht ausgeführt wird. Daher können Sie den Pfad nehmen, der der Implementierung des Codes am nächsten kam, und fragen, ob dieser Pfad geändert werden kann, damit er in die richtige Richtung verläuft.



Aber in dem Moment, in dem Sie versuchen, alle Pfade gleichzeitig zu erstellen, beginnen Einschränkungen, die unlösbar werden. Daher können Sie jeweils eine Funktion ausführen, während Sie alle Pfade in einer Funktion zusammen lernen können. Wenn Sie versuchen, große Blöcke zu erstellen, können Sie im Allgemeinen alle möglichen Wege erkunden.

Das Wichtigste ist, dass Sie für jeden Zweig Ihre Einschränkungen überprüfen und feststellen, ob dieser Zweig wirklich in beide Richtungen gehen kann. Wenn sie nicht beide Wege gehen kann, sparen Sie Zeit und Mühe, indem Sie nicht in die Richtung gehen, in die sie nicht gehen kann. Außerdem erinnere ich mich nicht an die spezifischen Strategien, mit denen sie Wege finden, die mit größerer Wahrscheinlichkeit zu sehr guten Ergebnissen führen. Es ist jedoch sehr wichtig, im Anfangsstadium die falschen Zweige abzuschneiden.

Bisher haben wir hauptsächlich über „Spielzeugcode“ gesprochen, über ganzzahlige Variablen, über Zweige, über sehr einfache Dinge. Aber was passiert, wenn Sie ein komplexeres Programm haben? Was passiert insbesondere, wenn Sie ein Programm haben, das eine Menge enthält?



In der Vergangenheit war der Hüfthaufen der Fluch aller Softwareanalysen, da die sauberen und eleganten Dinge in Fortrans Zeit vollständig explodieren, wenn Sie versuchen, sie mit C-Programmen auszuführen, in denen Sie links und rechts Speicher zuweisen. Dort haben Sie Überlagerungen und all das Durcheinander, das mit dem Programm verbunden ist, mit zugewiesenem Speicher und mit arithmetischen Zeigern. Dies ist einer der Bereiche, in denen die symbolische Ausführung eine hervorragende Fähigkeit besitzt, über Programme nachzudenken.

Wie machen wir das? Vergessen wir für einen Moment die Zweige und den Kontrollfluss. Wir haben hier ein einfaches Programm. Es reserviert etwas Speicher, macht ihn ungültig und erhält einen neuen Zeiger y vom Zeiger x. Dann schreibt sie etwas in y und prüft, ob der im Zeiger y gespeicherte Wert dem im Zeiger x gespeicherten Wert entspricht.

Basierend auf den Grundkenntnissen von C können Sie sehen, dass diese Prüfung nicht durchgeführt wird, da x zurückgesetzt wird und y = 25 ist, sodass x einen anderen Ort angibt. Bisher ist bei uns alles in Ordnung.
Die Art und Weise, wie wir den Heap modellieren und wie der Heap auf den meisten Systemen modelliert wird, verwendet die Heap-Darstellung in C, wo es sich nur um eine gigantische Adressbasis handelt, ein gigantisches Array, in das Sie Ihre Daten einfügen können.
Dies bedeutet, dass wir unser Programm als einen sehr großen globalen Datensatz darstellen können, der als MEM bezeichnet wird. Dies ist ein Array, das im Wesentlichen Adressen Werten zuordnet. Eine Adresse ist nur ein 64-Bit-Wert. Und was passiert, wenn Sie etwas von dieser Adresse gelesen haben? Dies hängt davon ab, wie Sie den Speicher modellieren.

Wenn Sie es auf Byte-Ebene modellieren, erhalten Sie ein Byte. Wenn Sie es auf Wortebene modellieren, erhalten Sie ein Wort. Abhängig von der Art der Fehler, an denen Sie interessiert sind, und davon, ob Sie über die Speicherzuordnung besorgt sind oder nicht, werden Sie sie etwas anders modellieren, aber normalerweise ist der Speicher nur ein Array von Adresse zu Wert.



Die Adresse ist also nur eine ganze Zahl. In gewisser Weise spielt es keine Rolle, was C von der Adresse hält, es ist nur eine 64-Bit- oder 32-Bit-Ganzzahl, abhängig von Ihrem Computer. Es ist einfach ein Wert, der in diesem Speicher indiziert ist. Und was Sie speichern können, können Sie aus diesem Speicher lesen.

Daher werden Dinge wie Zeigerarithmetik einfach zu Ganzzahlarithmetik. In der Praxis gibt es einige Schwierigkeiten, da in C die Zeigerarithmetik die Zeigertypen kennt und sie proportional zur Größe zunehmen. Als Ergebnis erhalten wir die folgende Zeile:

y = x + 10;  sizeof (int)



Aber was wirklich zählt, ist, was passiert, wenn Sie in den Speicher schreiben und aus ihm lesen. Basierend auf dem Zeiger, dass 25 in y geschrieben werden soll, nehme ich ein Array von Speicher und indiziere es mit y. Und ich schreibe 25 in diesen Speicherort.

Dann gehe ich zur Anweisung MEM [y] = MEM [x] über, lese den Wert von Position y im Speicher, lese den Wert von Position x im Speicher und vergleiche sie miteinander. Also überprüfe ich, ob sie übereinstimmen oder nicht.

Dies ist eine sehr einfache Annahme, mit der Sie von einem Programm, das Heap verwendet, zu einem Programm wechseln können, das dieses gigantische globale Array verwendet, das Speicher darstellt. Dies bedeutet, dass Sie jetzt, wenn Sie über Programme sprechen, die den Heap verwalten, wirklich nicht über Programme sprechen müssen, die den Heap verwalten. Sie werden es perfekt schaffen, über Arrays und nicht über Haufen zu sprechen.

Hier ist eine weitere einfache Frage. Was ist mit der Malloc-Funktion? Sie können einfach die Malloc-Implementierung in C verwenden, alle hervorgehobenen Seiten im Auge behalten, alles, was freigegeben wurde, im Auge behalten, nur eine kostenlose Liste haben und das ist genug. Es stellt sich heraus, dass Sie für viele Zwecke und für viele Arten von Fehlern kein Malloc benötigen, um komplex zu sein.

Tatsächlich können Sie von malloc, das so aussieht: x = malloc (sizeof (int) * 100), zu malloc dieser Art wechseln:

POS = 1
Int malloc (int n) {
rv = POS
POS + = n;
}}

Was einfach sagt: "Ich werde den Zähler für den nächsten freien Speicherplatz im Speicher speichern, und wenn jemand nach einer Adresse fragt, gebe ich ihm diesen Ort und erhöhe diese Position und kehre dann rv zurück." In diesem Fall wird das Malloc im traditionellen Sinne völlig ignoriert.



In diesem Fall wird kein Speicher freigegeben. Die Funktion bewegt sich einfach weiter und weiter aus dem Speicher und immer weiter und weiter, und hier endet sie ohne Freigabe. Es ist ihr auch egal, dass es Speicherbereiche gibt, in denen es sich nicht lohnt zu schreiben, da spezielle Adressen von besonderer Bedeutung für das Betriebssystem reserviert sind.

Es modelliert nichts, was das Schreiben der Malloc-Funktion kompliziert macht, sondern nur auf einer bestimmten Abstraktionsebene, wenn Sie versuchen, über einen komplexen Code zu sprechen, der Zeigermanipulationen ausführt.

Gleichzeitig ist es Ihnen egal, wie viel Speicher freigegeben wird, aber Sie sind besorgt darüber, ob das Programm beispielsweise außerhalb eines Puffers schreiben wird. In diesem Fall kann diese Malloc-Funktion recht gut sein.



Und das passiert tatsächlich sehr, sehr oft, wenn Sie echten Code symbolisch ausführen. Ein sehr wichtiger Schritt ist die Modellierung der Funktionen Ihrer Bibliothek. Die Art und Weise, wie Sie Bibliotheksfunktionen modellieren, hat einerseits einen großen Einfluss auf die Leistung und Skalierbarkeit der Analyse, andererseits wirkt sich dies auch auf die Genauigkeit aus.

Wenn Sie also ein solches „Spielzeug“ -Modell wie dieses haben, wird es sehr schnell reagieren, aber gleichzeitig gibt es bestimmte Arten von Fehlern, die Sie nicht bemerken können. In diesem Modell ignoriere ich beispielsweise Verteilungen vollständig, sodass möglicherweise eine Fehlermeldung angezeigt wird, wenn jemand Zugriff auf nicht zugewiesenen Speicherplatz erhält. Daher werde ich im wirklichen Leben niemals dieses Malloc-Modell von Mickey Mouse verwenden.

Es ist also immer ein Gleichgewicht zwischen Genauigkeit der Analyse und Effizienz. Und je komplexer die Modelle von Standardfunktionen wie Malloc werden, desto weniger skalierbar ist ihre Analyse. Für einige Fehlerklassen benötigen Sie jedoch diese einfachen Modelle. Daher sind verschiedene Bibliotheken in C von großer Bedeutung, die benötigt werden, um zu verstehen, was ein solches Programm tatsächlich tut.

Daher haben wir das Problem des Denkens über den Heap reduziert, indem wir über das Programm mit Arrays nachgedacht haben, aber ich habe Ihnen nicht wirklich gesagt, wie Sie über das Programm mit Arrays argumentieren sollen. Es stellt sich heraus, dass die meisten SMT-Löser die Array-Theorie unterstützen.



Die Idee ist, dass wenn a ein Array ist, es eine Notation gibt, mit der Sie dieses Array nehmen und ein neues Array erstellen können, wobei der Speicherort i auf den Wert e aktualisiert wird. Das ist klar?

Wenn ich also ein Array a habe und diese Aktualisierungsoperation durchführe und dann versuche, den Wert von k zu lesen, bedeutet dies, dass der Wert von k gleich dem Wert von k im Array a ist, wenn k von i verschieden ist und er gleich e ist. wenn k gleich i ist.

Das Aktualisieren eines Arrays bedeutet, dass Sie das alte Array nehmen und mit einem neuen Array aktualisieren müssen. Wenn Sie eine Formel haben, die die Theorie der Arrays enthält, habe ich deshalb mit einem Null-Array begonnen, das überall einfach durch Nullen dargestellt wird.



Dann schreibe ich 5 an Position i und 7 an Position j, danach lese ich aus k und überprüfe, ob es 5 ist oder nicht. Dann kann es erweitert werden, indem die Definition für etwas verwendet wird, das zum Beispiel sagt: „Wenn k i und k y ist, während k sich von j unterscheidet, dann ist es ja 5, andernfalls nicht 5 ".

In der Praxis erweitern SMT-Löser dies nicht nur auf viele Boolesche Formeln, sondern verwenden diese Hin- und Her-Strategie zwischen dem SAT-Löser und der Engine, die in der Lage ist, über die Array-Theorie zu sprechen, um diese Arbeit auszuführen.

Wichtig ist, dass Sie unter Verwendung dieser Theorie von Arrays mit derselben Strategie, die wir zum Generieren von Formeln für Ganzzahlen angewendet haben, tatsächlich Formeln generieren können, die Array-Logik, Array-Aktualisierungen, Array-Achsen und Array-Iteration enthalten. Und solange Sie Ihren Pfad korrigieren, sind diese Formeln sehr einfach zu generieren.
Wenn Sie Ihre Pfade nicht korrigieren, aber eine Formel erstellen möchten, die dem Durchgang des Programms entlang aller Pfade entspricht, ist dies ebenfalls relativ einfach. Das einzige, mit dem Sie sich befassen müssen, ist eine spezielle Art von Schleifen.

Wörterbücher und Karten lassen sich auch sehr einfach mit undefinierten Funktionen modellieren. Tatsächlich ist die Theorie der Arrays selbst nur ein Sonderfall einer unbestimmten Funktion. Mit Hilfe solcher Funktionen können kompliziertere Dinge getan werden. Im modernen SMT-Solver gibt es eine integrierte Unterstützung für Überlegungen zu Mengen und Mengenoperationen. Dies kann sehr nützlich sein, wenn Sie über ein Programm sprechen, das die Berechnung von Mengen umfasst.

Beim Entwerfen eines dieser Werkzeuge ist die Modellierungsphase sehr wichtig. Und es geht nicht nur darum, wie Sie komplexe Programmfunktionen bis auf Ihre Theorien modellieren, zum Beispiel Dinge wie das Reduzieren von Heaps auf Arrays. Der Punkt ist auch, welche Theorien und Löser Sie verwenden. Es gibt eine große Anzahl von Theorien und Lösern mit unterschiedlichen Beziehungen, für die ein angemessener Kompromiss zwischen Effizienz und Kosten gewählt werden muss.



Die meisten praktischen Werkzeuge halten sich an die Theorie der Bitvektoren und können bei Bedarf die Theorie der Arrays zur Modellierung von Heaps verwenden. Im Allgemeinen versuchen praktische Werkzeuge, komplexere Theorien wie die Mengenlehre zu vermeiden. Dies liegt daran, dass sie in einigen Fällen normalerweise weniger skalierbar sind, wenn Sie nicht mit einem Programm arbeiten, für das diese Art von Tool wirklich erforderlich ist.

Zielgruppe: Worauf konzentrieren sich Entwickler neben der Untersuchung der symbolischen Leistung?

: — , . , , , , . , .

, , . , , , , , , , .

, — , , . , , — , JavaScript Python, . , .



, Python. , , : «, , , ». .

, , , , , .
, , , - , , .

, , , . , , Microsoft Word, , , .

, , , , .

, . , , - , - . , , . , .


Die Vollversion des Kurses finden Sie hier .

, . ? ? , 30% entry-level , : VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps $20 ? ( RAID1 RAID10, 24 40GB DDR4).

VPS (KVM) E5-2650 v4 (6 Kerne) 10 GB DDR4 240 GB SSD 1 Gbit / s bis Dezember kostenlos, wenn Sie für einen Zeitraum von sechs Monaten bezahlen, können Sie hier bestellen.

Dell R730xd 2 ? 2 Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100 $249 ! . c Dell R730xd 5-2650 v4 9000 ?