MIT-Kurs "Computer Systems Security". Vorlesung 10: Symbolische Ausführung, Teil 2

Massachusetts Institute of Technology. Vorlesung # 6.858. "Sicherheit von Computersystemen." Nikolai Zeldovich, James Mickens. 2014 Jahr

Computer Systems Security ist ein Kurs zur Entwicklung und Implementierung sicherer Computersysteme. Die Vorträge behandeln Bedrohungsmodelle, Angriffe, die die Sicherheit gefährden, und Sicherheitstechniken, die auf jüngsten wissenschaftlichen Arbeiten basieren. Zu den Themen gehören Betriebssystemsicherheit, Funktionen, Informationsflussmanagement, Sprachsicherheit, Netzwerkprotokolle, Hardwaresicherheit und Sicherheit von Webanwendungen.

Vorlesung 1: „Einführung: Bedrohungsmodelle“ Teil 1 / Teil 2 / Teil 3
Vorlesung 2: „Kontrolle von Hackerangriffen“ Teil 1 / Teil 2 / Teil 3
Vorlesung 3: „Pufferüberläufe: Exploits und Schutz“ Teil 1 / Teil 2 / Teil 3
Vorlesung 4: „Trennung von Privilegien“ Teil 1 / Teil 2 / Teil 3
Vorlesung 5: „Woher kommen Sicherheitssysteme?“ Teil 1 / Teil 2
Vorlesung 6: „Chancen“ Teil 1 / Teil 2 / Teil 3
Vorlesung 7: „Native Client Sandbox“ Teil 1 / Teil 2 / Teil 3
Vorlesung 8: „Netzwerksicherheitsmodell“ Teil 1 / Teil 2 / Teil 3
Vorlesung 9: „Sicherheit von Webanwendungen“ Teil 1 / Teil 2 / Teil 3
Vorlesung 10: „Symbolische Ausführung“ Teil 1 / Teil 2 / Teil 3

Zielgruppe: Anscheinend haben Sie nicht darüber gesprochen, wie Bits zum Speichern einer Ganzzahl int verwendet werden.

Professor: Das ist eine sehr gute Frage. Und es hat wirklich damit zu tun, wie Sie Ihre Grenzen definieren, oder? Wenn Sie sich also von Anfang an unser einfaches Beispiel ansehen, werden Sie feststellen, dass wir das Vorhandensein von ganzen Zahlen angenommen haben, die wir in der Grundschule gelernt haben. Gleichzeitig haben wir uns entschlossen, Überlauffehler vollständig zu ignorieren. Wenn Sie sich für Überlauffehler interessieren und es für Sie wichtig ist, dass keine solchen Fehler vorliegen, hilft die Verwendung von mathematisch ganzzahligen Zahlen nicht, das Problem zu beheben.



Sie müssen diese Größen nicht als Ganzzahlen, sondern als Bitvektoren darstellen. Wenn Sie sie als Bitvektoren darstellen, sollten Sie eine breitere Sicht der Dinge verwenden. Hier kehren wir zu den SMT-Lösern zurück. Ein Aspekt der modularen Theorie ist, dass der Löser selbst mit verschiedenen Theorien erweiterbar ist.

Die beliebtesten Theorien sind Bitvektortheorien fester Länge. Dies bedeutet, dass Sie, wenn Sie Ihre Formeln in der Theorie der Bitvektoren fester Länge interpretieren, zuerst die Länge der Bitvektoren einstellen müssen. Das heißt, Sie müssen explizit angeben, dass dies für Bitvektoren mit einer Länge von 32 Bit oder 8 Bit oder 64 Bit verwendet wird.



Es gibt eine andere Theorie namens TOA-Array-Theorie. Und wir werden ein bisschen mehr darüber reden. Im Gegensatz zur Theorie der Bitvektoren, die für Dinge fester Länge ausgelegt ist, ist die Theorie der Arrays für Sammlungen gedacht, deren Größe a priori unbekannt ist.

In der Praxis verwendet niemand die Theorie der Arrays, um beispielsweise ganze Zahlen zu modellieren, weil sie zu teuer ist. Über ein Problem zu sprechen ist viel teurer, wenn man seine Grenzen nicht kennt. Daher verwenden Menschen in der Regel die Theorie einer festen Länge von Bitvektoren bei der Diskussion von ganzen Zahlen oder sogar Symbolen.

Eine andere sehr weit verbreitete Theorie ist die Theorie der reellen Ganzzahlarithmetik und insbesondere der linearen Ganzzahlarithmetik.



Die Leute mögen diese Theorie sehr, weil sie eine effektive Argumentation liefert, aber sie ist nicht allzu gut, wenn Sie über Programme sprechen, weil Sie sich hier wirklich um Überlaufprobleme kümmern. Aber diese Theorie ist für viele Dinge weit verbreitet.

Eine andere häufig verwendete Theorie ist die Theorie nicht interpretierter Funktionen. Was bedeutet diese Theorie?



Es bedeutet, dass Sie eine bestimmte Formel haben. In dieser Formel wissen Sie, dass Sie eine Funktion aufrufen, aber Sie wissen nichts über diese Funktion, außer der Tatsache, dass Sie dieselbe Ausgabe erhalten, wenn Sie eine Eingabe in sie einfügen.

Es stellt sich heraus, dass dies sehr nützlich ist, wenn Sie über Dinge wie Gleitkomma-Code, Modellierung, Sinus, Cosinus und Quadratwurzeln nachdenken. Detaillierte Diskussionen über solche Dinge können sehr zeitaufwändig und teuer sein. Mit dieser Theorie können Sie jedoch sagen: "Sehen Sie, es ist mir egal, was die Sinusfunktion bewirkt. Es ist mir egal, was genau sie herausgeben wird. Ich muss nur wissen, dass ich, wenn ich die Sinusfunktion an verschiedenen Stellen des Programms mit einer bestimmten Eingabe aufrufe, am Ausgang Daten der gleichen Art erhalte. Das ist genug für mich, um über mein Programm nachzudenken. “

Daher sind die häufigsten Operationen bei der Analyse realer Systeme Bitvektoren, die mit Ganzzahlen, Protokollen und Zeigern arbeiten. Tatsächlich werden Zeiger häufig durch eine Ganzzahl dargestellt, da Sie manchmal keine Bitvektoren für Zeiger festlegen. Aber manchmal müssen Sie dies tun, und dann können Sie keine ganzen Zahlen mehr verwenden.

Deshalb haben wir untersucht, was ein SMT-Solver für Sie tun kann. Wie funktioniert es wirklich? Was ist in ihnen, das sie arbeiten lässt?

Tatsächlich verlassen sich SMT-Löser auf unsere Fähigkeit, die Machbarkeitsprobleme von SAT-Booleschen Formeln zu lösen, auf die Fähigkeit, Probleme zu berücksichtigen, die nur mit rein booleschen Einschränkungen und booleschen Variablen verbunden sind, und uns mitzuteilen, ob Sie sicherstellen, dass das Programm die diesen booleschen Variablen zugewiesenen Werte zuweist oder nicht. .

Dies ist etwas, das viele, viele Jahre lang ältere Schüler unterrichtete und sagte, dass dies tatsächlich eine NP-vollständige Aufgabe ist, und in Fällen, in denen etwas auf SAT hinausläuft, sollten Sie dies nicht tun. Es stellt sich jedoch heraus, dass wir tatsächlich sehr gute SAT-Löser haben.

Ich werde Ihnen also die Grundidee der Funktionsweise von SAT-Lösern erläutern. Es liegt in der Tatsache, dass Sie alle Ihre Einschränkungen für boolesche Variablen in die Datenbank aufnehmen. Möglicherweise können Sie die kleinen Buchstaben auf dem Bildschirm nicht klar sehen, aber das ist alles, was ich tun kann.



Ich werde es im Verlauf der Aktion kommentieren und darüber sprechen, und später werde ich die Folien veröffentlichen, damit Sie sehen können, was dort geschrieben steht.

Hier in der SAT-Aufgabe haben wir also alle diese Variablen, die boolesche Unbekannte darstellen, richtig? Wir wollen wissen, ob es möglich ist, dass X gleichzeitig wahr ist (X = TRUE) und Y wahr ist und Z wahr ist. Das sind unsere Unbekannten. Darüber hinaus liegen alle Einschränkungen in normaler Konjunktivform vor. Dies bedeutet, dass alle unsere Einschränkungen entweder in Form von X1 = wahr oder X2 = wahr oder X3 = wahr vorliegen.



In dieser Form haben wir alle unsere Einschränkungen, die besagen, dass entweder X1 wahr oder X2 falsch oder X3 falsch ist. Sie erinnern sich wahrscheinlich aus der diskreten Mathematik daran, dass jede Boolesche Formel in normaler Verbindungsform dargestellt werden kann. Dies bedeutet, dass Sie jede Darstellung, die Sie zur Darstellung von Booleschen Formeln verwenden, sehr einfach in dieses Format konvertieren können.

Wir haben also eine Datenbank mit vielen Einschränkungen dieses Formulars. Der SAT-Löser wählt eine dieser Variablen zufällig aus, vorausgesetzt, es ist X1. Und er wird sagen: „Warum nicht X1 auf wahr setzen? Ich weiß nichts über diese Einschränkungen, daher kann ich davon ausgehen, dass dies tatsächlich der Fall ist. " Und dann kommt es vor, dass Sie Einschränkungen haben, die beispielsweise angeben, dass entweder X1 falsch oder X7 wahr ist.

Wenn Sie also wissen, dass X1 wahr ist und Sie wissen, dass entweder X1 falsch oder X7 wahr ist, was wissen Sie über X7?

Teilnehmerin: Es muss wahr sein!

Professor: Ja, das muss wahr sein. Denn sonst wird diese Einschränkung nicht erfüllt. Jetzt haben Sie diesen Wert von X1 auf X7 verteilt. Angenommen, Sie wählen jetzt eine andere Zufallsvariable aus, z. B. X5.



Angenommen, Sie haben eine Einschränkung, die besagt: Entweder ist X7 falsch oder X6 ist wahr oder X5 ist falsch. Also habe ich X5 = wahr und X7 = wahr. Dies bedeutet, dass X6 jetzt auch wahr sein sollte. Denn sonst würde diese Einschränkung verletzt. Das System kommt daher zu dem Schluss, dass X6 wahr sein sollte, und setzt den Prozess fort, indem es die verfügbaren Überprüfungen durchführt und alle verfügbaren Angebote überprüft. Das System prüft, ob es andere Dinge gibt, die durch die von ihm durchgeführten Prüfungen impliziert werden. Und sie folgt diesen Bedeutungen, bis eines von zwei Dingen passiert.

Das erste ist, dass Sie weiterhin den Konsequenzen folgen und zufällige Dinge ausprobieren. Letztendlich legen Sie den Wert für jede Variable fest, ohne jemals auf einen Widerspruch zu stoßen. Also hast du alles richtig gemacht.

Das zweite - Sie sind mit einem Widerspruch konfrontiert und kehren dann zu der Bedingung zurück, die X4 wahr gemacht hat, mit Ausnahme der Bedingung, die X4 falsch gemacht hat. Es gibt jedoch eine Regel der Booleschen Algebra, die jeder kennen sollte: Eine Variable kann nicht gleichzeitig wahr und falsch sein.



Und es heißt, dass Sie mit einem Widerspruch konfrontiert sind. Offensichtlich haben Sie bei einer dieser zufälligen Aufgaben, die Sie zu erledigen versucht haben, etwas falsch gemacht.

Lassen Sie uns diesen Widerspruch analysieren und sehen, welche Art von Aufgaben zu diesem Widerspruch geführt haben. Lassen Sie uns basierend auf den Aufgaben, die zu diesem Widerspruch geführt haben, eine neue Konfliktklausel entwickeln, die diesen Widerspruch zusammenfasst.

Was passiert, wenn X1 falsch ist und X5 falsch ist und X9 auch falsch ist? Im Wesentlichen basiert dies auf dem, was ich aus diesen zufälligen Zuordnungen gelernt habe, bei denen ich herausgefunden habe, dass eines dieser Dinge wahr sein muss, dass es nicht sein kann, dass X1 wahr ist und X5 wahr ist und X9 wahr ist falsch, das kann nicht sein.

Ich weiß, dass dies nicht passieren kann, denn als ich es versuchte, explodierte alles und ich beendete das Programm mit einem Widerspruch.

Daher versucht der SAT-Solver, zufällige Aufgaben zu erledigen und zu überprüfen, wie sie ablaufen. Wenn er auf Widersprüche stößt, analysiert er die Konsequenzen, die zu diesen Widersprüchen geführt haben, und bildet letztendlich eine neue Einschränkung, die sicherstellt, dass der Löser nie wieder auf diesen bestimmten Widerspruch, dieses bestimmte Problem stößt.
Daher können wir uns den SAT-Solver als eine „Black Box“ vorstellen, die eine Boolesche Einschränkung ergibt und erkennen kann, ob sie zufriedenstellend ist oder nicht. SMT-Löser bauen auf den besten SAT-Lösern auf. Sie können die Kraft von SAT-Lösern nutzen, um NP-vollständige Probleme mit themenorientiertem Denken über unterstützte Theorien zu lösen.

Angenommen, Sie haben eine solche Formel, um eine Vorstellung davon zu bekommen, wie dies funktioniert.



Ist es machbar? Können wir einen befriedigenden Test für sie finden? Der SMT-Löser kann einen Teil dieser Formel trennen, was eine Argumentation in der Ganzzahltheorie erfordert. Wir verwenden Boolesche Strukturen, um Formeln zu trennen. Wir haben also die Formeln F1, F2, F3 und F4.



Dies ist eine rein logische, boolesche Aufgabe. Kann ich dafür eine zufriedenstellende Aufgabe finden? Der SAT-Löser kann sagen: "Ja, ich kann etwas finden, das diese Aufgabe erfüllt, indem ich F1 = wahr, F2 = wahr und F3 = wahr mache." Dies erfüllt die Spezifikation der Booleschen Formel.

\.

Jetzt haben wir also eine Frage, die wir dem Löser für einen bestimmten Bereich stellen können. In diesem Fall handelt es sich nur um einen linearen arithmetischen Löser. Wir können also zum linearen Löser des Theorie-Lösers gehen und sagen: „Der SAT-Löser behauptet, dass dies eine vernünftige Aufgabe ist und dass meine Formel erfüllt ist, wenn ich diese Aufgabe zum Laufen bringen kann.“

Ich kann sagen, dass F1 X> 5 ist, F2 Y <5 ist und F3 Y> X ist. Also kann ich den SAT-Löser fragen, ob es möglich ist, solche X und Y zu erhalten, so dass X> 5 ist, Y <ist 5, und in diesem Fall wäre Y> X? Dies ist eine Frage der rein linearen Arithmetik, es gibt keine boolesche Logik.

Und wie lautet die Antwort auf diese Frage? Nein. Es ist unmöglich, diese Bedingungen gleichzeitig zu erfüllen.
Es gibt also traditionelle Methoden zur Lösung linearer Probleme. Mit der Simplex-Methode können Sie beispielsweise Systeme linearer Ungleichungen lösen. Es gibt viele Methoden, mit denen Systeme linearer Ungleichungen gelöst werden können.



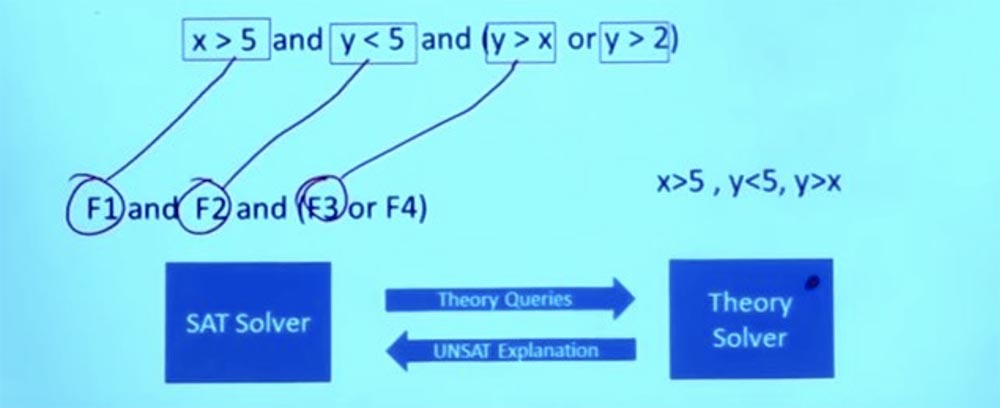
Der SAT-Löser sendet also theoretische Fragen an den Theorie-Löser. Das Fazit ist, dass Theory Solver Solver alles über diese Probleme wissen und eine genaue Antwort auf die Frage geben können, ob diese Bedingungen funktionieren.

In diesem Fall verarbeitet der theoretische Löser die Anforderung, stellt fest, dass diese Zuweisung von Bedingungen nicht funktionieren kann, kehrt zum SAT-Löser zurück und sagt: „Die Dinge, die Sie getan haben, werden nicht funktionieren“!

Aber er sagt nicht nur Ja oder Nein, sondern erklärt, warum etwas nicht funktioniert. Aus der Tatsache, dass diese Formeln nicht funktionieren, schließt der Theory Solver, dass F1 und F2 und F3 nicht gleichzeitig existieren können, und teilt dem SAT-Solver mit, dass sich diese 3 Formeln gegenseitig ausschließen.

Jetzt haben wir einige Informationen, die ich an den SAT-Löser zurückgeben und ihn fragen kann: „Hey, Sie können mir eine Lösung geben, die nicht nur die Einschränkung erfüllt, die wir zu Beginn hatten, sondern auch die neue Einschränkung, die die Theorie entdeckt hat Löser "?

Gibt es einen anderen Zweck, der diese beiden Einschränkungen erfüllt?



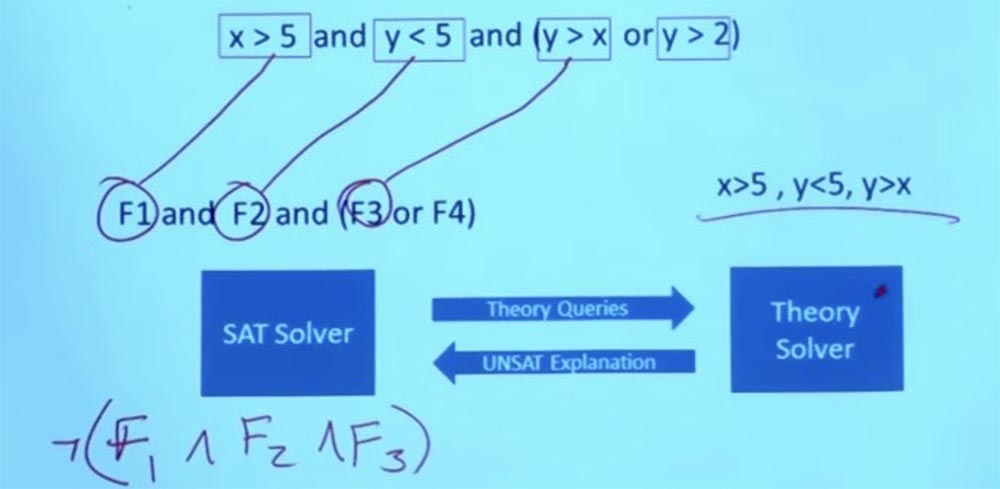
Also verwerfen wir die anfängliche Einschränkung X> 5, Y <5, Y> X, das stört uns nicht mehr.



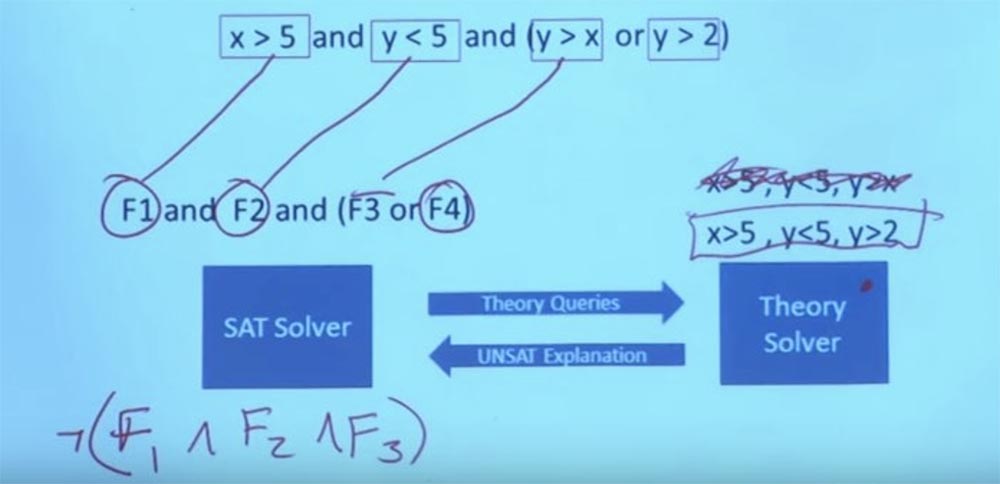
Wir haben eine neue Einschränkung, die wir auf unseren Theorielöser setzen können - X> 5, Y <5, Y> 2. Wir können Y gleich 3 und X gleich 6 machen, und dann wird es funktionieren. Jetzt haben Sie eine Aufgabe, die die Formel in der Theorie und die Boolesche Struktur dieses Zwecks erfüllt. Und damit kann das System zurückkommen und sagen: "Ja, dies ist die Aufgabe, die alle Ihre Einschränkungen erfüllt." Dies ist die Interaktion zwischen dem Theory Solver und dem SAT Solver. In Wirklichkeit bedeutet dies, über sehr, sehr große und sehr komplexe Boolesche Formeln sprechen zu können. Folgendes ermöglicht die symbolische Ausführung.

Nun werden wir uns mit der nächsten Frage befassen: Wie erfolgt der Übergang vom Programm zu den Einschränkungen, die wir dem SMT-Löser bieten können?

Zielgruppe: Ist der Bau eines SMT-Lösers NP-vollständig oder nicht?

Professor: Der SMT-Löser ist im Wesentlichen ein kanonisches NP-vollständiges Problem. Aber die meisten Löser unterstützen heutzutage bestimmte Theorien, die völlig unlösbar sind.

Zielgruppe: Wie gehen Sie in Ihrem System mit diesem Problem um?

Professor: Nun, am Ende erhalten Sie eine Einschränkung, die aus diesem Programm erstellt wurde. Sie werden es dem SMT-Solver geben. Und die Tatsache, dass es sich um NP-abgeschlossene Aufgaben handelt oder dass sie unbefriedigend sind, bedeutet, dass Sie mit etwas Glück innerhalb von Sekunden eine Antwort erhalten. Aber wenn Sie Pech haben, kann es länger dauern, als die Erschaffung des Universums gedauert hat.



Teilnehmerin: Kommt es vor, dass die Aufgaben des linearen Systems den SAT nicht bestehen?

Professor: Ja, das passiert wirklich. Vorhandene Engineering-Tools machen es jedoch weniger verbreitet. Wir lösen keine zufälligen Probleme von SAT, wir lösen keine vollständig zufälligen Probleme von Bitvektoren.

Wir lösen Probleme mit einer bestimmten Struktur, damit eine Person sie betrachten und sicher sein kann, dass sie funktioniert. Wir versuchen, einige Argumente in seinem Kopf zu schaffen, um zu verstehen, warum dies funktioniert hat. Und SAT-Löser verwenden diese Struktur. Ihr Problem hat möglicherweise eine Million Boolesche Variablen, aber in Wirklichkeit hängen die meisten dieser Variablen stark von den Werten des jeweils anderen ab. Somit ist die Anzahl der Freiheitsgrade in dem Problem tatsächlich viel geringer als von Millionen von Variablen vorgeschlagen.

Teilnehmerin: Sie sagen, dass dies keine Prüfungsfrage ist, sondern das wirkliche Leben. Sobald jemand dieses System gebaut hat, sollte es funktionieren und Sinn machen. Dies wird also wahrscheinlich keine der unnötigen theoretischen Beschimpfungen sein.

Professor: das war's. Wenn Sie dieses Tool verwenden, legen Sie in der Praxis daher immer Zeitüberschreitungen fest. Im Allgemeinen geschieht alles, weil Exponentialität nicht bedeutet, dass Sie dies nicht tun können. Exponentialität, das heißt, wenn eine Funktion durch eine andere Funktion eingeschränkt wird, bedeutet einfach, dass es eine Mauer gibt, vor der diese Dinge funktionieren, und sie werden wirklich sehr schnell funktionieren. Exponentialität funktioniert in beide Richtungen.



Wenn Sie sich von dieser Wand entfernen, wachsen die Dinge sehr schnell, aber wenn Sie sich kleineren oder einfacheren Problemen nähern, beschleunigen sich diese Probleme auch sehr, sehr schnell. Dies bedeutet, dass viele Probleme sehr schnell enden. Und dann tritt das Problem-Timeout auf. Es geht darum, die Dinge so zu gestalten, dass zu den Problemen, die schnell enden, diejenigen gehören, die praktische Vorteile bringen. Dies sind Probleme, die Sie auf die Sicherheitslücken Ihres Systems, auf Fehler, auf Pfade, die Sie möglicherweise noch nicht untersucht haben, oder auf Eingaben hinweisen, die Ihre Pfade verletzen, wenn Sie sie nicht im Voraus untersucht haben.

Wir wissen also, wie man von einer Formel, von einer Reihe von Einschränkungen zu einer Antwort übergeht, die entweder sagt: "Ja, diese Formel hat eine Lösung, und hier ist es, dies ist eine Lösung." Oder er wird sagen: "Diese Formel ist unbefriedigend, weil es keine Eingabe gibt, die Ihre Aufgaben erfüllt." Wie bekommen wir die Formel aus dem Programm?

Wenn Sie eine symbolische Ausführung durchführen, gehen Sie zum Zweig und wissen nicht, in welche Richtung er gehen wird. In diesem Fall gibt es zwei Möglichkeiten. — , , , .

, , . , SMT-. . , .

: « , , , , ».

, , . . , .

, . , , . , – , . ? , .



, , t=0 false.



, , ? : , , .

, , , , , , .

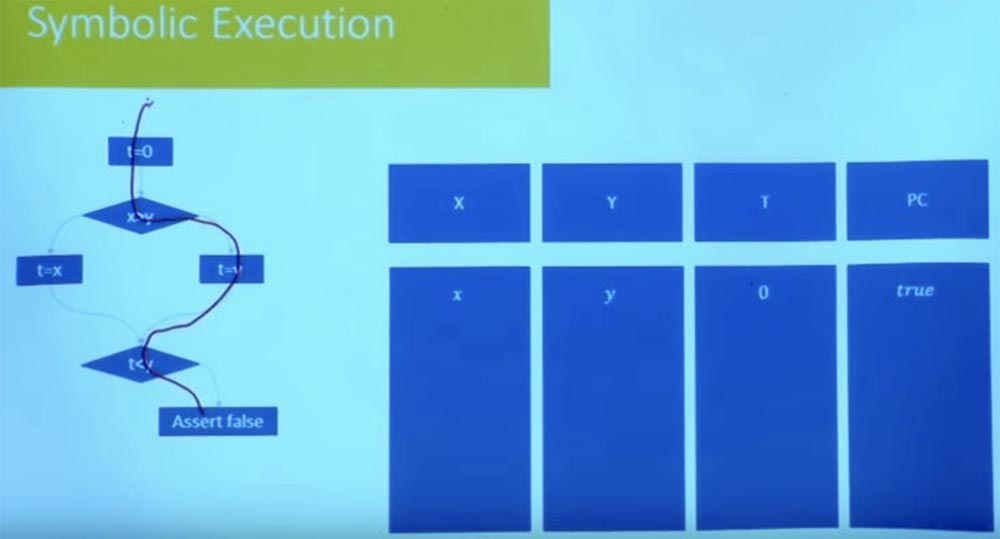
, , t = 0, x, y 0. , . , , X , Y.

, X > Y.



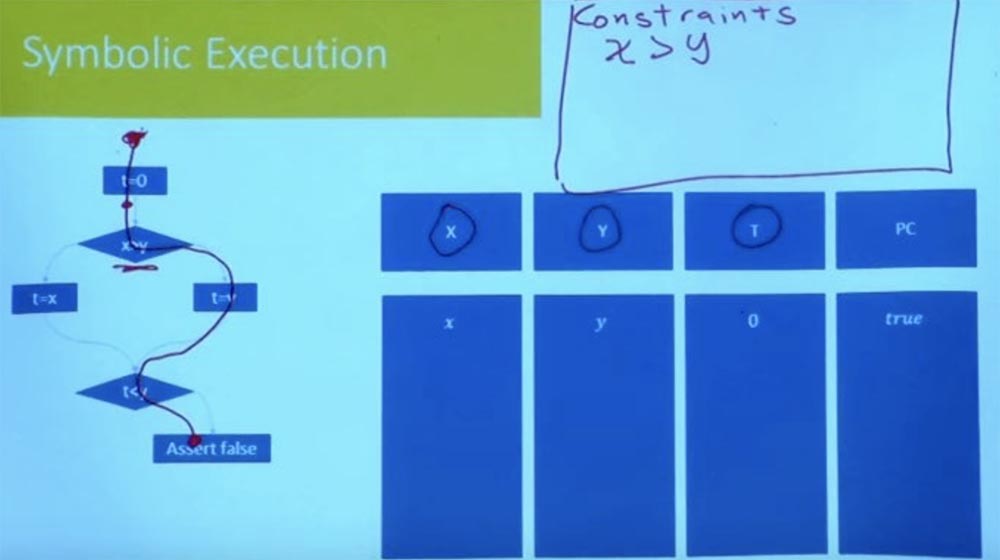
55:00

MIT « ». 10: « », 3


Die Vollversion des Kurses finden Sie hier .

, . ? ? , 30% entry-level , : VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps $20 ? ( RAID1 RAID10, 24 40GB DDR4).

VPS (KVM) E5-2650 v4 (6 Kerne) 10 GB DDR4 240 GB SSD 1 Gbit / s bis Dezember kostenlos, wenn Sie für einen Zeitraum von sechs Monaten bezahlen, können Sie hier bestellen.

Dell R730xd 2 mal günstiger? Nur wir haben 2 x Intel Dodeca-Core Xeon E5-2650v4 128 GB DDR4 6 x 480 GB SSD 1 Gbit / s 100 TV von 249 US-Dollar in den Niederlanden und den USA! Lesen Sie mehr über den Aufbau eines Infrastrukturgebäudes. Klasse mit Dell R730xd E5-2650 v4 Servern für 9.000 Euro für einen Cent?