Identifizieren Sie Betrug mithilfe des Enron-Datensatzes. Teil 2, das beste Modell finden

Ich präsentiere Ihnen den zweiten Teil des Artikels über die Suche nach mutmaßlichem Betrug basierend auf Daten aus Enron Dataset. Wenn Sie den ersten Teil nicht gelesen haben, können Sie sich hier damit vertraut machen.

Jetzt werden wir über den Prozess des Aufbaus, Optimierens und Auswählens eines Modells sprechen, das die Antwort gibt: Lohnt es sich, eine Person des Betrugs zu verdächtigen?

Zuvor haben wir einen der offenen Datensätze analysiert, der Informationen zu Verdächtigen im Fall Enron und Betrug darin enthält. Außerdem wurde die Verzerrung in den Anfangsdaten korrigiert, Lücken (NaN) wurden gefüllt, wonach die Daten normalisiert und die Auswahl der Attribute abgeschlossen wurde.

Das Ergebnis war vielen bekannt:

• X_train und y_train - die für das Training verwendete Stichprobe (111 Datensätze);
• X_test und y_test - ein Beispiel, anhand dessen die Richtigkeit der Vorhersagen unserer Modelle überprüft wird (28 Einträge).

Apropos Modelle ... Um anhand einiger Anzeichen, die seine Aktivitäten charakterisieren, richtig vorherzusagen, ob es sich lohnt, eine Person zu verdächtigen, verwenden wir die Klassifizierung. Die wichtigsten Modelltypen zur Lösung von Problemen in diesem Segment können von Sklearn übernommen werden:

• Naive Bayes (naiver Bayes-Klassifikator);
• SVM (Referenzvektormaschine);
• K-nächste Nachbarn (Methode zum Finden der nächsten Nachbarn);
• Zufälliger Wald (zufälliger Wald);
• Neuronales Netz.

Es gibt auch ein Bild, das ihre Anwendbarkeit recht gut veranschaulicht:

Unter ihnen gibt es einen Entscheidungsbaum (Entscheidungsbaum), der vielen bekannt ist, aber vielleicht macht es in einer Aufgabe keinen Sinn, diese Methode zusammen mit Random Forest zu verwenden, einem Ensemble von Entscheidungsbäumen. Ersetzen Sie es daher durch die logistische Regression, die als Klassifizierer fungieren und eine der erwarteten Optionen (0 oder 1) erzeugen kann.

Starten Sie

Wir initialisieren alle genannten Klassifikatoren mit Standardwerten:

from sklearn.naive_bayes import GaussianNB from sklearn.linear_model import LogisticRegression from sklearn.neighbors import KNeighborsClassifier from sklearn.svm import SVC from sklearn.neural_network import MLPClassifier from sklearn.ensemble import RandomForestClassifier random_state = 42 gnb = GaussianNB() svc = SVC() knn = KNeighborsClassifier() log = LogisticRegression(random_state=random_state) rfc = RandomForestClassifier(random_state=random_state) mlp = MLPClassifier(random_state=random_state) 

Wir werden sie auch so gruppieren, dass es bequemer ist, mit ihnen als Aggregat zu arbeiten, als Code für jede Person zu schreiben. Zum Beispiel können wir sie alle auf einmal trainieren:

 classifiers = [gnb, svc, knn, log, rfc, mlp] for clf in classifiers: clf.fit(X_train, y_train) 

Nachdem die Modelle trainiert worden waren, war es Zeit für den ersten Test ihrer Vorhersagequalität. Zusätzlich visualisieren wir unsere Ergebnisse mit Seaborn:

 from sklearn.metrics import accuracy_score def calculate_accuracy(X, y): result = pd.DataFrame(columns=['classifier', 'accuracy']) for clf in classifiers: predicted = clf.predict(X_test) accuracy = round(100.0 * accuracy_score(y_test, predicted), 2) classifier = clf.__class__.__name__ classifier = classifier.replace('Classifier', '') result = result.append({'classifier': classifier, 'accuracy': accuracy}, ignore_index=True) print('Accuracy is {accuracy}% for {classifier_name}'.format(accuracy=accuracy, classifier_name=classifier)) result = result.sort_values(['classifier'], ascending=True) plt.subplots(figsize=(10, 7)) sns.barplot(x="classifier", y='accuracy', palette=cmap, data=result) 

Werfen wir einen Blick auf die allgemeine Vorstellung von der Genauigkeit der Klassifikatoren:

 calculate_accuracy(X_train, y_train) 

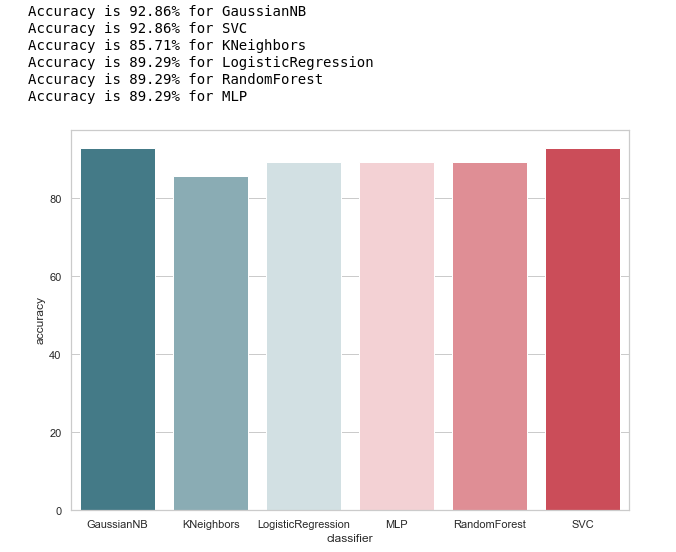
Auf den ersten Blick sieht es ziemlich gut aus, die Genauigkeit der Vorhersagen auf der Testprobe schwankt um 90%. Es scheint, dass die Aufgabe brillant ist!

 def QuaziAlgo(features): return 0 

Bevor wir uns jedoch schmeicheln, wollen wir eine Verwirrungsmatrix für die Vorhersageergebnisse erstellen:

 from sklearn.metrics import confusion_matrix def make_confussion_matrices(X, y): matrices = {} result = pd.DataFrame(columns=['classifier', 'recall']) for clf in classifiers: classifier = clf.__class__.__name__ classifier = classifier.replace('Classifier', '') predicted = clf.predict(X_test) print(f'{predicted}-{classifier}') matrix = confusion_matrix(y_test,predicted,labels=[1,0]) matrices[classifier] = matrix.T return matrices 

Wir berechnen die Fehlermatrizen für jeden Klassifikator und sehen zusammen mit diesen, was sie vorhergesagt haben:

 matrices = make_confussion_matrices(X_train,y_train) 

Selbst eine textuelle Darstellung des Ergebnisses der Arbeit der Klassifikatoren reicht aus, um zu verstehen, dass eindeutig etwas schief gelaufen ist.

Die Methode der nächsten Nachbarn ergab überhaupt keinen einzigen Verdächtigen in der Testprobe. Es stellen sich zwei Fragen:

1. Was ist der Grund für dieses Verhalten des KNeighbors-Klassifikators?
2. Warum haben wir Fehlermatrizen erstellt, wenn wir sie nicht verwenden, sondern nur die Ergebnisse der Vorhersage betrachten?

Schau genauer hin

Beginnen wir mit der zweiten Frage. Versuchen wir, unsere Fehlermatrizen zu visualisieren und die Daten in grafischem Format darzustellen, um zu verstehen, wo der Klassifizierungsfehler auftritt:

 import itertools from collections import Iterable def draw_confussion_matrices(row,col,matrices,figsize = (16,12)): fig, (axes) = plt.subplots(row,col, sharex='col', sharey='row',figsize=figsize ) if any(isinstance(i, Iterable) for i in axes): axes = list(itertools.chain.from_iterable(axes)) idx = 0 for name,matrix in matrices.items(): df_cm = pd.DataFrame( matrix, index=['True','False'], columns=['True','False'], ) ax = axes[idx] fig.subplots_adjust(wspace=0.1) sns.heatmap(df_cm, annot=True,cmap=cmap,cbar=False ,fmt="d",ax=ax,linewidths=1) ax.set_title(name) idx += 1 

Wir zeigen sie in 2 Zeilen und 3 Spalten an:

 draw_confussion_matrices(2,3,matrices) 

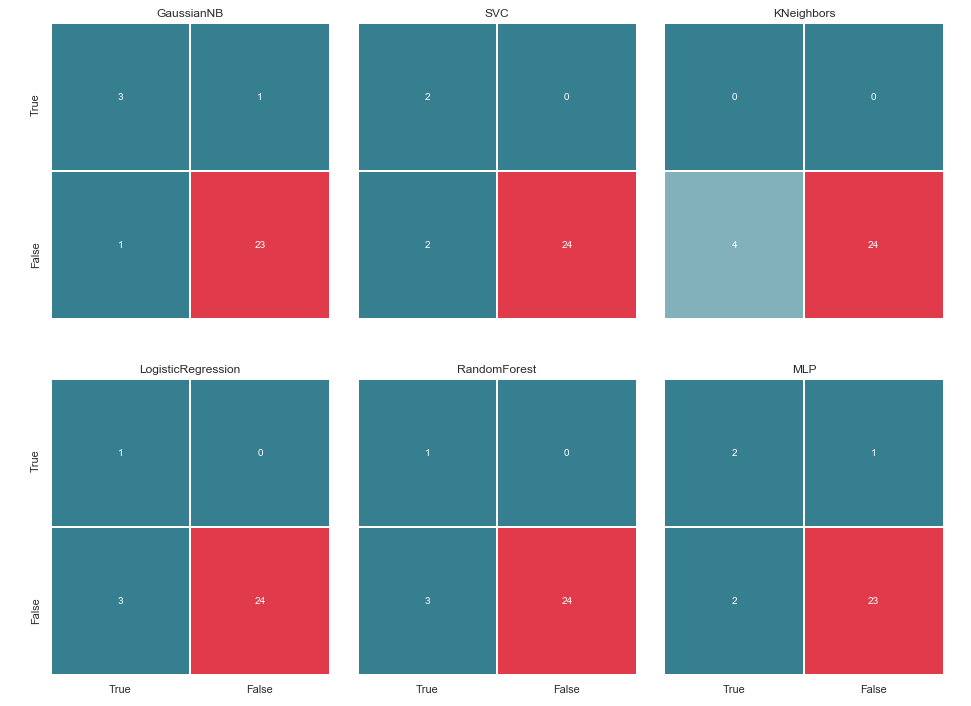
Bevor Sie fortfahren, sollten Sie einige Erläuterungen geben. Die Bezeichnung True, die sich links von der Fehlermatrix eines bestimmten Klassifikators befindet, bedeutet, dass der Klassifikator die Person als verdächtig angesehen hat. Der Wert False bedeutet, dass die Person nicht verdächtig ist. In ähnlicher Weise geben Richtig und Falsch am unteren Rand des Bildes einen realen Zustand an, der möglicherweise nicht mit der Entscheidung des Klassifikators übereinstimmt.

Zum Beispiel sehen wir, dass KNeighbors Entscheidungen mit einer Vorhersagegenauigkeit von 85,71% mit der tatsächlichen Situation übereinstimmten, als 24 Personen, die keinen Verdacht hatten, vom Klassifikator in eine ähnliche Liste aufgenommen wurden. Aber auch 4 Personen aus der Liste der Verdächtigen wurden in diese Liste aufgenommen. Wenn dieser Klassifikator Entscheidungen getroffen hätte, hätte vielleicht jemand das Gericht meiden können.

Daher sind Fehlermatrizen ein sehr gutes Werkzeug, um zu verstehen, was bei Klassifizierungsproblemen schief gelaufen ist. Ihr Hauptvorteil ist die Sichtbarkeit, und deshalb appellieren wir an sie.

Metriken

Im Allgemeinen kann dies durch das folgende Bild veranschaulicht werden:

Und was ist in diesem Fall TP, TN, FP und eine Art FN?

$$$TP \ - \ wahr-positiv \ Lösung \\ TN \ - \ wahr-negativ \ Lösung \\ FP \ - \ falsch-positiv \ Lösung \\ FN \ - \ falsch-negativ \ Lösung$

Mit anderen Worten, wir bemühen uns sicherzustellen, dass die Antworten des Klassifikators und der tatsächliche Sachverhalt übereinstimmen. Das heißt, um sicherzustellen, dass alle Zahlen zwischen den Zellen TP und TN (echte Lösungen) verteilt sind und nicht in FN und FP (falsche Lösungen) fallen.

Und da es sich um Abkürzungen handelt, ist es an der Zeit, sich an die Metriken Genauigkeit (Präzision) und Vollständigkeit (Rückruf) zu erinnern.

Wenn Sie von der formalen Aufzeichnung abweichen, kann Präzision ausgedrückt werden als:

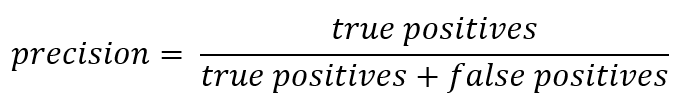
Mit anderen Worten, es wird ein Konto darüber geführt, wie viele positive Antworten vom Klassifizierer korrekt sind. Je höher die Genauigkeit, desto geringer die Anzahl der Fehlertreffer (die Genauigkeit beträgt 1, wenn keine FPs vorhanden sind).

Rückruf wird allgemein dargestellt als:

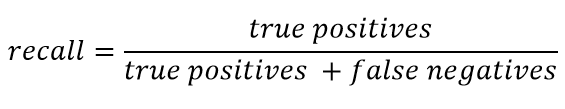
Rückruf kennzeichnet die Fähigkeit des Klassifikators, so viele positive Antworten wie möglich zu „erraten“. Je höher die Vollständigkeit, desto niedriger die FN.

Normalerweise versuchen sie, ein Gleichgewicht zwischen beiden herzustellen, aber in diesem Fall wird der Präzision die Priorität vollständig eingeräumt. Der Grund: ein humanistischerer Ansatz, der Wunsch, die Anzahl der Fehlalarme zu minimieren und infolgedessen zu vermeiden, dass der Verdacht auf die Unschuldigen fällt.

Wir berechnen die Genauigkeit für unsere Klassifikatoren:

 from sklearn.metrics import precision_score def calculate_precision(X, y): result = pd.DataFrame(columns=['classifier', 'precision']) for clf in classifiers: predicted = clf.predict(X_test) precision = precision_score(y_test, predicted, average='macro') classifier = clf.__class__.__name__ classifier = classifier.replace('Classifier', '') result = result.append({'classifier': classifier, 'precision': precision}, ignore_index=True) print('Precision is {precision} for {classifier_name}'.format(precision=round(precision,2), classifier_name=classifier)) result = result.sort_values(['classifier'], ascending=True) plt.subplots(figsize=(10, 7)) sns.barplot(x="classifier", y='precision', palette=cmap, data=result) calculate_precision(X_train, y_train) 

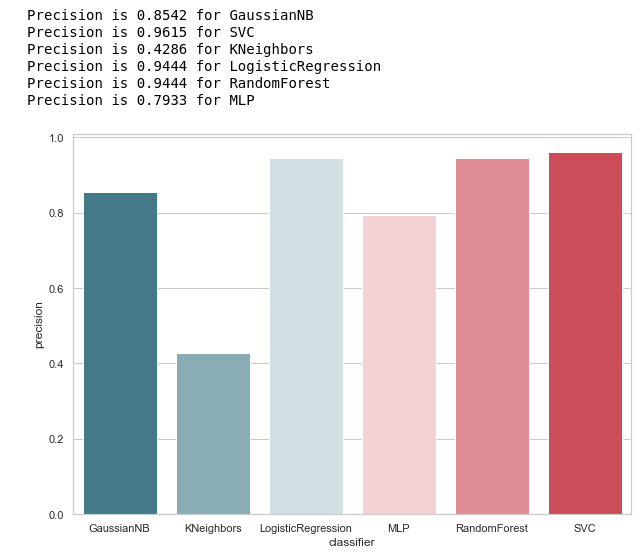
Wie aus der Abbildung hervorgeht, stellte sich heraus, dass die Genauigkeit von KNeighbors am niedrigsten war, da der TP-Wert am niedrigsten ist.

Gleichzeitig gibt es einen guten Artikel über Metriken zum Habré, und diejenigen, die tiefer in dieses Thema eintauchen möchten, sollten sich damit vertraut machen.

Hyperparameterauswahl

Nachdem wir die Metrik gefunden haben, die den ausgewählten Bedingungen am besten entspricht (wir reduzieren die Anzahl der FPs), können wir zur ersten Frage zurückkehren: Was ist der Grund für dieses Verhalten des KNeighbors-Klassifikators?

Der Grund liegt in den Standardeinstellungen, mit denen dieses Modell erstellt wurde. Und höchstwahrscheinlich könnten viele zu diesem Zeitpunkt ausrufen: Warum mit Standardparametern trainieren? Es gibt spezielle Auswahlwerkzeuge, zum Beispiel das häufig verwendete GridSearchCV.
Ja, das ist es, und es ist an der Zeit, darauf zurückzugreifen.

Aber vorher entfernen wir den Bayes'schen Klassifikator von unserer Liste. Es erlaubt eine FP, und gleichzeitig akzeptiert dieser Algorithmus keine variablen Parameter, wodurch sich das Ergebnis nicht ändert.

 classifiers.remove(gnb) 

Feinabstimmung

Wir definieren ein Parameterraster für jeden Klassifikator:

 parameters = {'SVC':{'kernel':('linear', 'rbf','poly'), 'C':[i for i in range(1,11)],'random_state': (random_state,)}, 'KNeighbors':{'algorithm':('ball_tree', 'kd_tree'), 'n_neighbors':[i for i in range(2,20)]}, 'LogisticRegression':{'penalty':('l1', 'l2'), 'C':[i for i in range(1,11)],'random_state': (random_state,)}, 'RandomForest':{'n_estimators':[i for i in range(10,101,10)],'random_state': (random_state,)}, 'MLP':{'activation':('relu','logistic'),'solver':('sgd','lbfgs'),'max_iter':(500,1000), 'hidden_layer_sizes':[(7,),(7,7)],'random_state': (random_state,)}} 

Außerdem wollte ich auf die Anzahl der Schichten / Neuronen in MLP achten.
Es wurde beschlossen, sie nicht durch erschöpfende Suche aller möglichen Werte festzulegen, sondern dennoch auf der Formel zu basieren:

$$$N_h = \ frac {N_s} {(\ alpha * (N_i + N_o))} = \ frac {117} {(2 * (7 + 1))} \ ca. 7$

Ich möchte sofort sagen, dass Training und Kreuzvalidierung nur für das Trainingsmuster durchgeführt werden. Ich gehe davon aus, dass es eine Meinung gibt, dass Sie dies für alle Daten tun können, wie im Beispiel mit Iris Dataset. Meiner Meinung nach ist dieser Ansatz jedoch nicht ganz gerechtfertigt, da es nicht möglich sein wird, den Ergebnissen der Überprüfung an einer Testprobe zu vertrauen.

Wir werden die Optimierung durchführen und unsere Klassifikatoren durch ihre verbesserte Version ersetzen:

 from sklearn.model_selection import GridSearchCV warnings.filterwarnings('ignore') for idx,clf in enumerate(classifiers): classifier = clf.__class__.__name__ classifier = classifier.replace('Classifier', '') params = parameters.get(classifier) if not params: continue new_clf = clf.__class__() gs = GridSearchCV(new_clf, params, cv=5) result =gs.fit(X_train, y_train) print(f'The best params for {classifier} are {result.best_params_}') classifiers[idx] = result.best_estimator_ 

Nachdem wir eine Metrik für die Bewertung ausgewählt und GridSearchCV durchgeführt haben, können wir die letzte Linie ziehen.

Zusammenfassend

Fehlermatrix v.2

 matrices = make_confussion_matrices(X_train,y_train) draw_confussion_matrices(1,2,first_row,figsize = (10.5,6)) draw_confussion_matrices(1,3,second_row,figsize = (16,6)) 

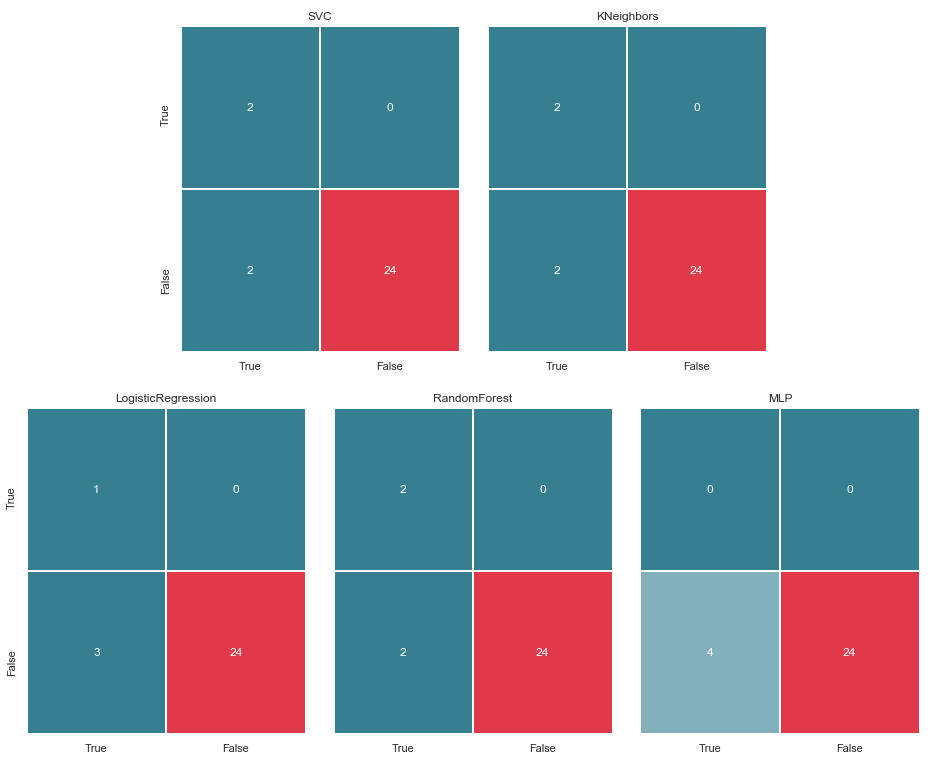
Wie aus der Matrix ersichtlich ist, zeigte MLP einen Abbau und ging davon aus, dass die Testprobe keine Verdächtigen enthielt. Random Forest gewann an Genauigkeit und korrigierte die Parameter für False Negative und True Positive. Und KNeighbors zeigte eine Verbesserung der Vorhersage. Die Prognose für andere hat sich nicht geändert.

Genauigkeit v.2

Jetzt hat keiner unserer aktuellen Klassifikatoren Fehler mit False Positive, was eine gute Nachricht ist. Wenn wir jedoch alles in der Sprache der Zahlen ausdrücken, erhalten wir das folgende Bild:

 calculate_precision(X_train, y_train) 

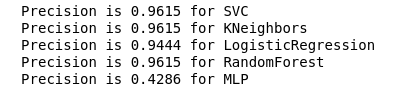
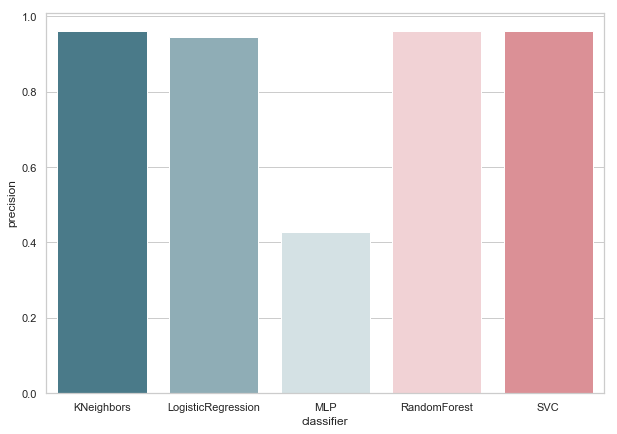
Es wurden 3 Klassifikatoren mit der höchsten Präzisionsbewertung identifiziert. Und sie haben die gleichen Werte, basierend auf der Fehlermatrix. Welcher Klassifikator soll gewählt werden?

Wer ist besser

Es scheint mir, dass dies eine ziemlich schwierige Frage ist, auf die es keine universelle Antwort gibt. Mein Standpunkt in diesem Fall würde jedoch ungefähr so ​​aussehen:

1. Der Klassifikator sollte in seiner technischen Implementierung so einfach wie möglich sein. Dann hat er ein geringeres Risiko für eine Umschulung (wahrscheinlich ist dies bei MLP passiert). Daher ist dies kein zufälliger Wald, da dieser Algorithmus ein Ensemble von 30 Bäumen ist und daher von diesen abhängt. Im Einklang mit einer der Ideen von Python Zen: Einfach ist besser als komplex.

2. Nicht schlecht, wenn der Algorithmus intuitiv war. Das heißt, KNeighbors wird einfacher wahrgenommen als SVMs mit potenziellem mehrdimensionalem Raum.
Was wiederum einer anderen Aussage ähnelt: explizit ist besser als implizit.

Daher ist KNeighbors mit 3 Nachbarn meiner Meinung nach der beste Kandidat.

Dies ist das Ende des zweiten Teils, in dem die Verwendung des Enron-Datensatzes als Beispiel für die Klassifizierungsaufgabe beim maschinellen Lernen beschrieben wird. Basierend auf den Materialien aus dem Kurs Einführung in maschinelles Lernen über Udacity. Es gibt auch ein Python-Notizbuch , das die gesamte beschriebene Abfolge von Aktionen widerspiegelt.