Spieltheorie: Entscheidungsfindung mit Beispielen bei Kotlin

Die Spieltheorie ist eine mathematische Disziplin, die die Modellierung der Aktionen von Spielern in Betracht zieht, die ein Ziel haben, nämlich die Auswahl der optimalen Strategien für das Verhalten in einem Konflikt. Auf Habré wurde dieses Thema bereits behandelt , aber heute werden wir einige seiner Aspekte genauer besprechen und Beispiele für Kotlin betrachten.

Eine Strategie besteht also aus einer Reihe von Regeln, die je nach Situation die Wahl einer Vorgehensweise für jeden persönlichen Schritt bestimmen. Die optimale Spielerstrategie ist die Strategie, die die beste Position in einem gegebenen Spiel sicherstellt, d. H. maximale Verstärkung. Wenn das Spiel mehrmals wiederholt wird und zusätzlich zu persönlichen, zufälligen Zügen enthält, liefert die optimale Strategie den maximalen durchschnittlichen Gewinn.

Die Aufgabe der Spieltheorie ist es, die optimalen Strategien für die Spieler zu identifizieren. Die Hauptannahme, auf deren Grundlage optimale Strategien gefunden werden, ist, dass der Gegner (oder die Gegner) nicht weniger intelligent ist als der Spieler selbst und alles tut, um sein Ziel zu erreichen. Die Berechnung eines vernünftigen Gegners ist nur eine der möglichen Positionen im Konflikt, aber in der Spieltheorie ist es das, was in den Grundstein gelegt wird.

Es gibt Spiele mit der Natur, bei denen nur ein Teilnehmer seinen Gewinn maximiert. Spiele mit der Natur sind mathematische Modelle, bei denen die Wahl der Lösung von der objektiven Realität abhängt. Zum Beispiel Verbrauchernachfrage, Naturzustand usw. "Natur" ist ein verallgemeinertes Konzept eines Gegners, der seine eigenen Ziele nicht verfolgt. In diesem Fall werden mehrere Kriterien verwendet, um die optimale Strategie auszuwählen.
In Spielen mit der Natur gibt es zwei Arten von Aufgaben:

1. die Aufgabe, Entscheidungen unter Risikobedingungen zu treffen, wenn die Wahrscheinlichkeiten bekannt sind, mit denen die Natur jeden der möglichen Zustände akzeptiert;
2. Entscheidungsaufgaben unter unsicheren Bedingungen, wenn es nicht möglich ist, Informationen über die Wahrscheinlichkeiten des Auftretens von Naturzuständen zu erhalten.

Hier wird kurz auf diese Kriterien eingegangen.

Jetzt werden wir die Entscheidungskriterien in reinen Strategien betrachten und am Ende des Artikels das Spiel in gemischten Strategien durch die analytische Methode lösen.

Erklärung des Problems

Wir werden alle Entscheidungskriterien anhand eines durchgehenden Beispiels analysieren. Die Aufgabe ist folgende: Der Landwirt muss bestimmen, in welchen Anteilen er sein Feld mit drei Kulturen säen soll, ob der Ertrag dieser Kulturen und damit der Gewinn davon abhängt, wie der Sommer sein wird: kühl und regnerisch, normal oder heiß und trocken. Der Landwirt berechnete je nach Wetterlage einen Nettogewinn von 1 Hektar aus verschiedenen Kulturen. Das Spiel wird durch die folgende Matrix bestimmt:



Weiter werden wir diese Matrix in Form von Strategien präsentieren:

$$

$$U_ {1} = (0,2,5), U_ {2} = (2,3,1), U_ {3} = (4,3, -1)$$

Die gewünschte optimale Strategie wird mit bezeichnet $$$u_ {opt}$ . Wir werden das Spiel anhand der Kriterien Wald, Optimismus, Pessimismus, Savage und Hurwitz unter Unsicherheitsbedingungen und der Kriterien Bayes und Laplace unter Risikobedingungen lösen.

Wie oben erwähnt, werden die Beispiele auf Kotlin sein. Ich stelle fest, dass es im Allgemeinen Lösungen wie Gambit (geschrieben in C), Axelrod und PyNFG (geschrieben in Python) gibt, aber wir werden unser eigenes Fahrrad fahren, das auf dem Knie montiert ist, nur um ein wenig stilvoll, modisch und modisch zu stoßen Jugendprogrammiersprache.

Um die Lösung des Spiels programmgesteuert umzusetzen, werden wir mehrere Klassen einführen. Zunächst benötigen wir eine Klasse, mit der wir eine Zeile oder Spalte einer Spielmatrix beschreiben können. Die Klasse ist äußerst einfach und enthält eine Liste möglicher Werte (Alternativen oder Naturzustände) und den entsprechenden Namen. Das key wird sowohl zur Identifizierung als auch zum Vergleich verwendet, und bei der Implementierung der Dominanz wird ein Vergleich erforderlich sein.


Die Spielmatrix enthält Informationen zu Alternativen und Naturzuständen. Darüber hinaus werden einige Methoden implementiert, z. B. das Ermitteln der dominanten Menge und des Nettopreises des Spiels.


Wir beschreiben die Schnittstelle, die die Kriterien erfüllt

Entscheidungsfindung unter Unsicherheit

Entscheidungen angesichts von Unsicherheit zu treffen, deutet darauf hin, dass der Spieler nicht von einem vernünftigen Gegner abgelehnt wird.

Wald-Kriterium

Das Wald-Kriterium maximiert das schlechtestmögliche Ergebnis:

$$

$$u_ {opt} = max_ {i} min_ {j} [U]$$

Die Verwendung des Kriteriums versichert gegen das schlechteste Ergebnis, aber der Preis einer solchen Strategie ist der Verlust der Möglichkeit, das bestmögliche Ergebnis zu erzielen.

Betrachten Sie ein Beispiel. Für Strategien $$$U_ {1} = (0,2,5), U_ {2} = (2,3,1), U_ {3} = (4,3, -1)$ Finde die Tiefs und hol dir die nächsten drei $$$S = (0, 1, -1)$ . Das Maximum für das angegebene Tripel ist der Wert 1, daher ist nach dem Wald-Kriterium die Gewinnstrategie die Strategie $$$U_ {2} = (2,3,1)$ entsprechend der Pflanzkultur 2.

Die Software-Implementierung des Wald-Kriteriums ist einfach:

 class WaldCriteria(gameMatrix : GameMatrix) : ICriteria { val gameMatrix: GameMatrix init{ this.gameMatrix = gameMatrix } override fun optimum(): List<GameVector> { val mins = gameMatrix.alternatives.map { a -> Pair(a, a.min()) } val max = mins.maxWith( Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!)}) return mins .filter { m -> m.second == max!!.second } .map { m -> m.first } } } 

Aus Gründen der Klarheit werde ich zum ersten Mal zeigen, wie die Lösung wie ein Test aussehen würde:


Es ist leicht zu erraten, dass bei anderen Kriterien der Unterschied nur in der Erstellung des criteria .

Optimismuskriterium

Wenn der Spieler das Kriterium eines Optimisten verwendet, wählt er eine Lösung, die das beste Ergebnis liefert, während der Optimist davon ausgeht, dass die Spielbedingungen für ihn am günstigsten sind:

$$

$$u_ {opt} = max_ {i} max_ {j} [U]$$

Die Strategie eines Optimisten kann zu negativen Konsequenzen führen, wenn das maximale Angebot mit der minimalen Nachfrage übereinstimmt. Das Unternehmen kann Verluste erleiden, wenn es nicht verkaufte Produkte abschreibt. Gleichzeitig hat die Strategie des Optimisten eine bestimmte Bedeutung. Sie müssen sich beispielsweise nicht um unzufriedene Kunden kümmern, da eine mögliche Nachfrage immer befriedigt wird und daher der Standort der Kunden nicht beibehalten werden muss. Wenn die maximale Nachfrage erreicht wird, können Sie mit der Strategie des Optimisten den größtmöglichen Nutzen erzielen, während andere Strategien zu entgangenen Gewinnen führen. Dies bietet gewisse Wettbewerbsvorteile.

Betrachten Sie ein Beispiel. Für Strategien $$$U_ {1} = (0,2,5), U_ {2} = (2,3,1), U_ {3} = (4,3, -1)$ finde, finde das Maximum und erhalte die nächsten drei $$$S = (5, 3, 4)$ . Das Maximum für das angegebene Tripel ist der Wert 5, daher ist nach dem Kriterium des Optimismus die Gewinnstrategie die Strategie $$$U_ {1} = (0.2.5)$ entsprechend der Pflanzkultur 1.

Die Umsetzung des Optimismuskriteriums unterscheidet sich kaum vom Waldkriterium:

 class WaldCriteria(gameMatrix : GameMatrix) : ICriteria { val gameMatrix: GameMatrix init{ this.gameMatrix = gameMatrix } override fun optimum(): List<GameVector> { val mins = gameMatrix.alternatives.map { a -> Pair(a, a.min()) } val max = mins.maxWith( Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!)}) return mins .filter { m -> m.second == max!!.second } .map { m -> m.first } } } 

Kriterium des Pessimismus

Dieses Kriterium soll das kleinste Element der Spielmatrix aus den minimal möglichen Elementen auswählen:

$$

$$u_ {opt} = min_ {i} min_ {j} [U]$$

Das Pessimismuskriterium deutet darauf hin, dass die Entwicklung von Ereignissen für den Entscheidungsträger ungünstig sein wird. Bei Verwendung dieses Kriteriums lässt sich der Entscheidungsträger vom möglichen Kontrollverlust über die Situation leiten und versucht daher, potenzielle Risiken auszuschließen, indem er die Option mit minimaler Rentabilität wählt.

Betrachten Sie ein Beispiel. Für Strategien $$$U_ {1} = (0,2,5), U_ {2} = (2,3,1), U_ {3} = (4,3, -1)$ finde, finde das Minimum und erhalte die nächsten drei $$$S = (0, 1, -1)$ . Das Minimum für das angegebene Tripel ist der Wert -1, daher ist gemäß dem Kriterium des Pessimismus die Gewinnstrategie die Strategie $$$U_ {3} = (4.3, -1)$ entsprechend der Pflanzkultur 3.

Nachdem Sie Walds Kriterien und Optimismus kennengelernt haben, können Sie leicht erraten, wie die Klasse des Pessimismus-Kriteriums aussehen wird:

 class PessimismCriteria(gameMatrix : GameMatrix) : ICriteria { val gameMatrix: GameMatrix init{ this.gameMatrix = gameMatrix } override fun optimum(): List<GameVector> { val mins = gameMatrix.alternatives.map { a -> Pair(a, a.min()) } val min = mins.minWith( Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!)}) return mins .filter { m -> m.second == min!!.second } .map { m -> m.first } } } 

Wildes Kriterium

Das Savage-Kriterium (Kriterium eines pessimistischen Pessimisten) beinhaltet die Minimierung der größten entgangenen Gewinne, mit anderen Worten, das größte Bedauern über die entgangenen Gewinne wird minimiert:

$$

$$u_ {opt} = min_ {i} max_ {j} [S] \\ s_ {i, j} = (max \ begin {bmatrix} u_ {1, j} \\ u_ {2, j} \\. .. \\ u_ {n, j} \ end {bmatrix} - u_ {i, j})$$

In diesem Fall ist S die Matrix der Reue.

Die optimale Lösung gemäß dem Savage-Kriterium sollte das geringste Bedauern gegenüber den im vorherigen Schritt festgestellten Bedauern hervorrufen. Die dem gefundenen Dienstprogramm entsprechende Lösung ist optimal.

Zu den Merkmalen der erhaltenen Lösung gehören das garantierte Fehlen der größten Enttäuschungen und das garantierte Verringern der maximal möglichen Gewinne anderer Spieler.

Betrachten Sie ein Beispiel. Für Strategien $$$U_ {1} = (0,2,5), U_ {2} = (2,3,1), U_ {3} = (4,3, -1)$ eine Matrix des Bedauerns machen:



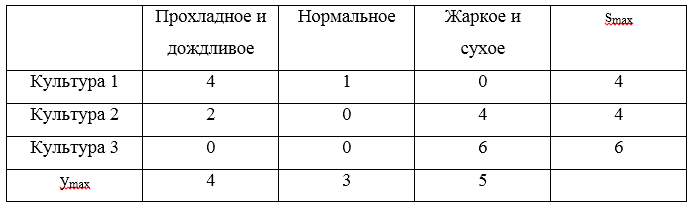
Drei maximale Bedauern $$$S = (4,4,6)$ . Der Mindestwert dieser Risiken beträgt 4, was den Strategien entspricht $$$U_ {1}$ und $$$U_ {2}$ .

Das Programmieren des Savage-Tests ist etwas schwieriger:

 class SavageCriteria(gameMatrix: GameMatrix) : ICriteria { val gameMatrix: GameMatrix init { this.gameMatrix = gameMatrix } fun GameMatrix.risk(): List<Pair<GameVector, Double?>> { val maxStates = this.natureStates.map { n -> Pair(n, n.values.max()) } .map { n -> n.first.key to n.second }.toMap() var am: MutableList<Pair<GameVector, List<Double>>> = mutableListOf() for (a in this.alternatives) { var v: MutableList<Double> = mutableListOf() for (i in 0..a.values.lastIndex) { val mn = maxStates.get(i) v.add(mn!! - a.values[i]) } am.add(Pair(a, v.toList())) } return am.map { m -> Pair(m.first, m.second.max()) } } override fun optimum(): List<GameVector> { val risk = gameMatrix.risk() val minRisk = risk.minWith(Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!) }) return risk .filter { r -> r.second == minRisk!!.second } .map { m -> m.first } } } 

Hurwitz-Kriterium

Das Hurwitz-Kriterium ist ein regulierter Kompromiss zwischen extremem Pessimismus und völligem Optimismus:

$$

$$u_ {opt} = max (\ gamma × A (k) + A (0) × (1 - \ gamma))$$

A (0) ist die Strategie des extremen Pessimisten, A (k) ist die Strategie des vollständigen Optimisten, $$$\ gamma = 1$ - Sollwert des Gewichtskoeffizienten: $$$0 \ leq \ gamma \ leq1$ ;; $$$\ gamma = 0$ - extremer Pessimismus, $$$\ gamma = 1$ - voller Optimismus.

Mit einer kleinen Anzahl von diskreten Strategien den gewünschten Wert des Gewichtskoeffizienten einstellen $$$\ gamma$ und runden Sie das Ergebnis unter Berücksichtigung der durchgeführten Diskretisierung auf den nächstmöglichen Wert.

Betrachten Sie ein Beispiel. Für Strategien $$$U_ {1} = (0,2,5), U_ {2} = (2,3,1), U_ {3} = (4,3, -1)$ . Wir gehen davon aus, dass der Optimismuskoeffizient $$$\ gamma = $ 0,$ . Machen Sie jetzt einen Tisch:



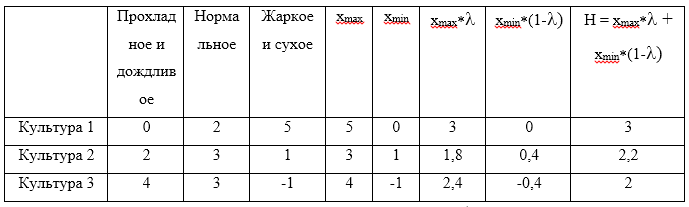
Der Maximalwert aus dem berechneten H ist der Wert 3, der der Strategie entspricht $$$U_ {1}$ .

Das Hurwitz-Kriterium ist bereits umfangreicher:

 class HurwitzCriteria(gameMatrix: GameMatrix, optimisticKoef: Double) : ICriteria { val gameMatrix: GameMatrix val optimisticKoef: Double init { this.gameMatrix = gameMatrix this.optimisticKoef = optimisticKoef } inner class HurwitzParam(xmax: Double, xmin: Double, optXmax: Double){ val xmax: Double val xmin: Double val optXmax: Double val value: Double init{ this.xmax = xmax this.xmin = xmin this.optXmax = optXmax value = xmax * optXmax + xmin * (1 - optXmax) } } fun GameMatrix.getHurwitzParams(): List<Pair<GameVector, HurwitzParam>> { return this.alternatives.map { a -> Pair(a, HurwitzParam(a.max()!!, a.min()!!, optimisticKoef)) } } override fun optimum(): List<GameVector> { val hpar = gameMatrix.getHurwitzParams() val maxHurw = hpar.maxWith(Comparator { o1, o2 -> o1.second.value.compareTo(o2.second.value) }) return hpar .filter { r -> r.second == maxHurw!!.second } .map { m -> m.first } } } 

Entscheidungsfindung in Gefahr

Entscheidungsfindungsmethoden können sich auf Kriterien für die Entscheidungsfindung unter Risikobedingungen unter folgenden Bedingungen stützen:

• Mangel an verlässlichen Informationen über die möglichen Folgen;
• das Vorhandensein von Wahrscheinlichkeitsverteilungen;
• Kenntnis der Wahrscheinlichkeit von Ergebnissen oder Konsequenzen für jede Entscheidung.

Wenn eine Entscheidung unter Risikobedingungen getroffen wird, werden die Kosten alternativer Entscheidungen durch Wahrscheinlichkeitsverteilungen beschrieben. In dieser Hinsicht basiert die Entscheidung auf der Verwendung des Erwartungswertkriteriums, nach dem alternative Lösungen im Hinblick auf die Maximierung des erwarteten Gewinns oder die Minimierung der erwarteten Kosten verglichen werden.

Das Kriterium des erwarteten Wertes kann entweder reduziert werden, um den erwarteten (durchschnittlichen) Gewinn zu maximieren oder um die erwarteten Kosten zu minimieren. In diesem Fall wird angenommen, dass der mit jeder alternativen Lösung verbundene Gewinn (Kosten) eine Zufallsvariable ist.

Die Formulierung solcher Aufgaben lautet normalerweise wie folgt: Eine Person wählt eine Aktion in einer Situation aus, in der zufällige Ereignisse das Ergebnis der Aktion beeinflussen. Der Spieler hat jedoch einige Kenntnisse über die Wahrscheinlichkeiten dieser Ereignisse und kann die rentabelste Kombination und Abfolge seiner Aktionen berechnen.

Um weiterhin Beispiele zu nennen, ergänzen wir die Spielmatrix mit Wahrscheinlichkeiten:



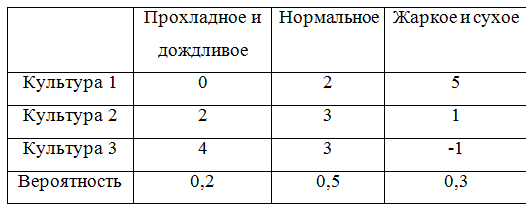
Um die Wahrscheinlichkeiten zu berücksichtigen, muss eine Klasse, die die Spielmatrix beschreibt, ein wenig überarbeitet werden. Es stellte sich in Wahrheit heraus, nicht sehr elegant, aber na ja.

Bayes-Kriterium

Das Bayes-Kriterium (Erwartungskriterium) wird bei Entscheidungsproblemen unter Risikobedingungen als Bewertung der Strategie verwendet $$$u_ {i}$ Die mathematische Erwartung der entsprechenden Zufallsvariablen erscheint. Nach dieser Regel ist die optimale Spielerstrategie $$$u_ {opt}$ wird aus der Bedingung gefunden:

$$

$$u_ {opt} = max_ {1 \ leq i \ leq n} M (u_ {i}) \\ M (u_ {i}) = max_ {1 \ leq i \ leq n} \ sum_ {j = 1} ^ m u_ {i, j} \ cdot y_ {j} ^ 0$$

Mit anderen Worten, ein Indikator für die Ineffizienz der Strategie $$$u_ {i}$ Nach dem Bayes-Kriterium für Risiken ist der Durchschnittswert (Erwartung) der Risiken der i-ten Zeile der Matrix $$$U$ deren Wahrscheinlichkeiten mit den Wahrscheinlichkeiten der Natur übereinstimmen. Dann ist die Strategie das optimale unter den reinen Strategien nach dem Bayes-Kriterium bezüglich der Risiken $$$u_ {opt}$ mit minimaler Ineffizienz, dh minimalem Durchschnittsrisiko. Das Bayes'sche Kriterium ist in Bezug auf Gewinne und in Bezug auf Risiken äquivalent, d.h. wenn die Strategie $$$u_ {opt}$ ist nach dem Bayes-Kriterium in Bezug auf Siege optimal, dann ist es nach dem Bayes-Kriterium in Bezug auf Risiken optimal und umgekehrt.

Fahren wir mit dem Beispiel fort und berechnen die mathematischen Erwartungen:

$$

$$M_1 = 0 \ cdot0.2 +2 \ cdot0.5 +5 \ cdot0.3 = 2.5; \\ M_2 = 2 \ cdot0.2 +3 \ cdot0.5 +1 \ cdot0.3 = 2.2 ; \\ M_4 = 0 \ cdot0.2 +3 \ cdot0.5 + (- 1) \ cdot0.3 = 2.0;$$

Die maximale mathematische Erwartung ist $$$M_1$ Daher ist eine Gewinnstrategie eine Strategie $$$U_1$ .

Software-Implementierung des Bayes-Kriteriums:

 class BayesCriteria(gameMatrix: ProbabilityGameMatrix) : ICriteria { val gameMatrix: ProbabilityGameMatrix init { this.gameMatrix = gameMatrix } fun ProbabilityGameMatrix.bayesProbability(): List<Pair<GameVector, Double?>> { var am: MutableList<Pair<GameVector, Double>> = mutableListOf() for (a in this.alternatives) { var alprob: Double = 0.0 for (i in 0..a.values.lastIndex) { alprob += a.values[i] * this.probabilities[i] } am.add(Pair(a, alprob)) } return am.toList(); } override fun optimum(): List<GameVector> { val risk = gameMatrix.bayesProbability() val maxBayes = risk.maxWith(Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!) }) return risk .filter { r -> r.second == maxBayes!!.second } .map { m -> m.first } } } 

Laplace-Kriterium

Das Laplace-Kriterium bietet eine vereinfachte Maximierung der mathematischen Nützlichkeitserwartung, wenn die Annahme der gleichen Wahrscheinlichkeit von Nachfragestufen gültig ist, wodurch die Notwendigkeit entfällt, echte Statistiken zu sammeln.

Im allgemeinen Fall werden bei Verwendung des Laplace-Kriteriums die Matrix der erwarteten Dienstprogramme und das optimale Kriterium wie folgt bestimmt:

$$

$$u_ {opt} = max [\ overline {U}] \\ \ overline {U} = \ begin {bmatrix} \ overline {u} _ {1} \\ \ overline {u} _ {2} \\. .. \\ \ overline {u} _ {n} \ end {bmatrix}, \ overline {u} _ {i} = \ frac {1} {n} \ sum_ {j = 1} ^ nu_ {i, j }$$

Betrachten Sie das Beispiel der Entscheidungsfindung nach dem Laplace-Kriterium. Wir berechnen das arithmetische Mittel für jede Strategie:

$$

$$\ overline {u} _ {1} = \ frac {1} {3} \ cdot (0 + 2 + 5) = 2.3 \\ \ overline {u} _ {2} = \ frac {1} { 3} \ cdot (2 + 3 + 1) = 2,0 \\ \ overline {u} _ {3} = \ frac {1} {3} \ cdot (4 + 3-1) = $ 2,$$

Die Gewinnstrategie ist also die Strategie $$$U_1$ .

Software-Implementierung des Laplace-Kriteriums:

 class LaplaceCriteria(gameMatrix: GameMatrix) : ICriteria { val gameMatrix: GameMatrix init { this.gameMatrix = gameMatrix } fun GameMatrix.arithemicMean(): List<Pair<GameVector, Double>> { return this.alternatives.map { m -> Pair(m, m.values.average()) } } override fun optimum(): List<GameVector> { val risk = gameMatrix.arithemicMean() val maxBayes = risk.maxWith(Comparator { o1, o2 -> o1.second.compareTo(o2.second) }) return risk .filter { r -> r.second == maxBayes!!.second } .map { m -> m.first } } } 

Gemischte Strategien. Analysemethode

Mit der Analysemethode können Sie das Spiel in gemischten Strategien lösen.Um einen Algorithmus zum Finden einer Lösung für ein Spiel durch eine analytische Methode zu formulieren, betrachten wir einige zusätzliche Konzepte.

Strategie$$U i dominiert die Strategie$U_{i}$$$U i - 1 , wenn alle$U_{i-1}$$$$u_{1..n} \in U_{i} \geq u_{1..n} \in U_{i-1}$ .Mit anderen Worten, wenn in einer Zeile einer Zahlungsmatrix alle Elemente größer oder gleich den entsprechenden Elementen einer anderen Zeile sind, dominiert die erste Zeile die zweite und wird als dominante Zeile bezeichnet. Und auch wenn in einer Spalte der Zahlungsmatrix alle Elemente kleiner oder gleich den entsprechenden Elementen einer anderen Spalte sind, dominiert die erste Spalte die zweite und wird als dominante Spalte bezeichnet.

Der niedrigste Preis des Spiels heißt$$$\alpha = max_i min_j u_{ij}$ .
Der Spitzenpreis des Spiels heißt $$$\beta = min_j max_i u_{ij}$ .

Jetzt können Sie einen Algorithmus zum Lösen des Spiels mit der Analysemethode formulieren:

1. Berechnen Sie den Boden $$α und oben$\alpha$$$β -Spielpreise. Wenn$\beta$$$α = β , dann schreibe die Antwort in reinen Strategien auf, wenn nicht, setze die Lösung weiter fort$\alpha = \beta$
2. Löschen Sie dominante Zeilen dominante Spalten. Es kann mehrere geben. An ihrer Stelle in der optimalen Strategie sind die entsprechenden Komponenten 0
3. Löse das Matrixspiel durch lineare Programmierung.

Um ein Beispiel zu geben, müssen Sie eine Klasse angeben, die die Lösung beschreibt


Und die Klasse, die die Lösung nach der Simplex-Methode ausführt. Da ich Mathematik nicht verstehe, habe ich die vorgefertigte Implementierung von Apache Commons Math verwendet


Jetzt führen wir die Lösung mit der Analysemethode aus. Zur Verdeutlichung nehmen wir eine andere Spielmatrix:

$$

$$\begin{pmatrix} 2& 4& 8& 5 \\ 6& 2& 4& 6\\ 3& 2& 5& 4 \end{pmatrix}$$

In dieser Matrix gibt es eine dominante Menge:
$$\begin{pmatrix} 2& 4\\ 6& 2\end{pmatrix}$$

Spielelösung $$( 0 , 33 ; 0 , 67 ; 0 ) mit einem Spielpreis von 3,33$(0,33; 0,67; 0)$

Anstelle einer Schlussfolgerung

Ich hoffe, dieser Artikel ist nützlich für diejenigen, die eine erste Annäherung an die Lösung von Spielen mit der Natur benötigen. Anstelle von Schlussfolgerungen ein Link zu GitHub .

Für das konstruktive Feedback wäre ich dankbar!