Hallo Habr! Ich präsentiere Ihnen die Titelseite der mehrarmigen Banditen lösen: Ein Vergleich von epsilon-gierigen und Thompson-Sampling- Artikeln.

Das mehrarmige Banditenproblem

Das mehrarmige Banditenproblem ist eine der grundlegendsten Aufgaben in der Wissenschaft der Lösungen. Dies ist nämlich das Problem der optimalen Allokation von Ressourcen unter Unsicherheitsbedingungen. Der Name "mehrarmiger Bandit" selbst stammt von alten Spielautomaten, die von Griffen gesteuert werden. Diese Sturmgewehre wurden als „Banditen“ bezeichnet, da sich die Menschen nach einem Gespräch normalerweise ausgeraubt fühlten. Stellen Sie sich nun vor, dass es mehrere solcher Maschinen gibt und die Chance, gegen verschiedene Autos zu gewinnen, unterschiedlich ist. Seit wir mit diesen Maschinen spielen, möchten wir feststellen, welche Chance höher ist, und diese Maschine häufiger als andere verwenden.

Das Problem ist folgendes: Wie können wir am effizientesten verstehen, welche Maschine am besten geeignet ist, und gleichzeitig viele Funktionen in Echtzeit ausprobieren? Dies ist kein theoretisches Problem, sondern ein Problem, mit dem ein Unternehmen ständig konfrontiert ist. Ein Unternehmen verfügt beispielsweise über mehrere Optionen für Nachrichten, die Benutzern angezeigt werden müssen (z. B. enthalten Nachrichten Anzeigen, Websites, Bilder), damit die ausgewählten Nachrichten eine bestimmte Geschäftsaufgabe maximieren (Conversion, Klickbarkeit usw.).

Ein typischer Weg, um dieses Problem zu lösen, besteht darin, A / B-Tests mehrmals durchzuführen . Das heißt, mehrere Wochen lang, um jede der Optionen gleich oft zu zeigen, und dann anhand statistischer Tests zu entscheiden, welche Option besser ist. Diese Methode eignet sich, wenn es nur wenige Optionen gibt, z. B. 2 oder 4. Wenn es jedoch viele Optionen gibt, wird dieser Ansatz unwirksam - sowohl bei Zeitverlust als auch bei entgangenem Gewinn.

Woher die verlorene Zeit kommt, sollte leicht zu verstehen sein. Mehr Optionen - mehr A / B-Tests sind erforderlich - mehr Zeit ist erforderlich, um eine Entscheidung zu treffen. Das Auftreten von entgangenen Gewinnen ist nicht so offensichtlich. Opportunitätsverlust (Opportunitätskosten) - die Kosten, die mit der Tatsache verbunden sind, dass wir anstelle einer Aktion eine andere durchgeführt haben, dh in einfachen Worten, dies ist das, was wir durch die Investition in A anstelle von B verloren haben. Die Investition in B ist der verlorene Gewinn aus der Investition in A. Das gleiche gilt für die Optionsprüfung. A / B-Tests sollten erst nach Abschluss unterbrochen werden. Dies bedeutet, dass der Experimentator nicht weiß, welche Option besser ist, bis der Test beendet ist. Es wird jedoch immer noch angenommen, dass eine Option besser ist als die andere. Dies bedeutet, dass wir durch die Verlängerung der A / B-Tests nicht die besten Optionen für eine ausreichend große Anzahl von Besuchern anzeigen (obwohl wir nicht wissen, welche Optionen nicht die besten sind), wodurch wir unseren Gewinn verlieren. Dies ist der verlorene Vorteil von A / B-Tests. Wenn es nur einen A / B-Test gibt, ist der entgangene Gewinn vielleicht überhaupt nicht groß. Eine große Anzahl von A / B-Tests bedeutet, dass wir unseren Kunden lange Zeit viele der nicht besten Optionen zeigen müssen. Es wäre besser, wenn Sie die schlechten Optionen schnell in Echtzeit wegwerfen könnten und nur dann, wenn nur noch wenige Optionen verfügbar sind, A / B-Tests für sie verwenden könnten.

Mit Samplern oder Agenten können Sie die Verteilung von Optionen schnell testen und optimieren. In diesem Artikel werde ich Ihnen die Thompson-Probenahme und ihre Eigenschaften vorstellen. Ich werde auch die Thompson-Abtastung mit dem epsilon-gierigen Algorithmus vergleichen, einer weiteren beliebten Option für das Problem der mehrarmigen Banditen. Alles wird von Grund auf in Python implementiert - der gesamte Code ist hier zu finden.

Kurzes Wörterbuch der Konzepte

• Agent, Sampler, Bandit ( Agent, Sampler, Bandit ) - ein Algorithmus, der Entscheidungen darüber trifft, welche Option angezeigt werden soll.
• Variante - eine andere Variante der Nachricht, die der Besucher sieht.
• Aktion - Die Aktion, die der Algorithmus ausgewählt hat (welche Option angezeigt werden soll).
• Verwenden ( Exploit ) - Treffen Sie eine Auswahl, um die Gesamtbelohnung basierend auf den verfügbaren Daten zu maximieren.
• Entdecken, erkunden - treffen Sie Entscheidungen, um die Amortisation für jede Option besser zu verstehen.
• Auszeichnung, Punkte ( Punktzahl, Belohnung ) - eine Geschäftsaufgabe, zum Beispiel Conversion oder Klickbarkeit. Der Einfachheit halber glauben wir, dass es binomial verteilt ist und entweder 1 oder 0 entspricht - geklickt oder nicht.
• Umgebung - der Kontext, in dem der Agent arbeitet - Optionen und deren „Rückzahlung“ für den Benutzer verborgen.
• Amortisation, Erfolgswahrscheinlichkeit ( Auszahlungsrate ) - eine versteckte Variable, die der Wahrscheinlichkeit entspricht, eine Punktzahl von 1 zu erhalten, für jede Option ist sie unterschiedlich. Aber der Benutzer sieht sie nicht.
• Versuchen Sie es ( Testversion ) - der Benutzer besucht die Seite.
• Bedauern ist der Unterschied zwischen dem besten Ergebnis aller verfügbaren Optionen und dem Ergebnis der im aktuellen Versuch verfügbaren Option. Je weniger Bedauern die bereits ergriffenen Maßnahmen sind, desto besser.
• Nachricht ( Nachricht ) - ein Banner, eine Seitenoption und mehr, von denen wir verschiedene Versionen ausprobieren möchten.
• Stichprobe - Die Erzeugung einer Stichprobe aus einer bestimmten Verteilung.

Entdecken und ausnutzen

Agenten sind Algorithmen, die nach einem Ansatz für die Entscheidungsfindung in Echtzeit suchen, um ein Gleichgewicht zwischen der Erkundung des Optionsraums und der Verwendung der besten Option zu erreichen. Dieses Gleichgewicht ist sehr wichtig. Der Optionsbereich muss untersucht werden, um eine Vorstellung davon zu erhalten, welche Option die beste ist. Wenn wir diese optimale Option zuerst entdeckt haben und sie dann die ganze Zeit verwenden, maximieren wir die Gesamtbelohnung, die uns aus der Umgebung zur Verfügung steht. Andererseits möchten wir auch andere mögliche Optionen untersuchen - was ist, wenn sie sich in Zukunft als besser herausstellen werden, aber wir wissen es noch nicht? Mit anderen Worten, wir möchten uns gegen mögliche Verluste versichern und versuchen, ein wenig mit suboptimalen Optionen zu experimentieren, um ihre Amortisation für sich selbst zu klären. Wenn ihre Amortisation tatsächlich höher ist, können sie häufiger angezeigt werden. Ein weiteres Plus bei der Untersuchung von Optionen besteht darin, dass wir nicht nur die durchschnittliche Amortisation besser verstehen können, sondern auch, wie grob die Amortisation verteilt ist, d. H. Wir können die Unsicherheit besser abschätzen.
Das Hauptproblem ist daher die Lösung - was ist der beste Ausweg aus dem Dilemma zwischen Exploration und Exploitation (Kompromiss zwischen Exploration und Exploitation).

Epsilon-gieriger Algorithmus

Ein typischer Ausweg aus diesem Dilemma ist der epsilon-gierige Algorithmus. "Gierig" bedeutet genau das, was Sie gedacht haben. Nach einer anfänglichen Periode, in der wir versehentlich Versuche unternehmen - beispielsweise 1000 Mal - wählt der Algorithmus eifrig die beste Option k in e Prozent der Versuche aus. Wenn beispielsweise e = 0,05 ist, wählt der Algorithmus in 95% der Fälle die beste Option aus und in den verbleibenden 5% der Fälle wählt er zufällige Versuche aus. Tatsächlich ist dies ein ziemlich effektiver Algorithmus, der jedoch möglicherweise nicht ausreicht, um den Raum der Optionen zu erkunden, und daher nicht ausreicht, um zu bewerten, welche Option die beste ist, um an einer suboptimalen Option festzuhalten. Lassen Sie uns im Code zeigen, wie dieser Algorithmus funktioniert.

Aber zuerst einige Abhängigkeiten. Wir müssen die Umwelt definieren. Dies ist der Kontext, in dem die Algorithmen ausgeführt werden. In diesem Fall ist der Kontext sehr einfach. Er ruft den Agenten an, damit der Agent entscheidet, welche Aktion er auswählen soll. Anschließend startet der Kontext diese Aktion und gibt die dafür erhaltenen Punkte an den Agenten zurück (der seinen Status irgendwie aktualisiert).

class Environment: def __init__(self, variants, payouts, n_trials, variance=False): self.variants = variants if variance: self.payouts = np.clip(payouts + np.random.normal(0, 0.04, size=len(variants)), 0, .2) else: self.payouts = payouts #self.payouts[5] = self.payouts[5] if i < n_trials/2 else 0.1 self.n_trials = n_trials self.total_reward = 0 self.n_k = len(variants) self.shape = (self.n_k, n_trials) def run(self, agent): """Run the simulation with the agent. agent must be a class with choose_k and update methods.""" for i in range(self.n_trials): # agent makes a choice x_chosen = agent.choose_k() # Environment returns reward reward = np.random.binomial(1, p=self.payouts[x_chosen]) # agent learns of reward agent.reward = reward # agent updates parameters based on the data agent.update() self.total_reward += reward agent.collect_data() return self.total_reward 

Punkte werden binomial mit der Wahrscheinlichkeit p in Abhängigkeit von der Anzahl der Aktionen verteilt (so wie sie kontinuierlich verteilt werden könnten, hätte sich die Essenz nicht geändert). Ich werde auch die BaseSampler-Klasse definieren - sie wird nur zum Speichern von Protokollen und verschiedenen Attributen benötigt.

 class BaseSampler: def __init__(self, env, n_samples=None, n_learning=None, e=0.05): self.env = env self.shape = (env.n_k, n_samples) self.variants = env.variants self.n_trials = env.n_trials self.payouts = env.payouts self.ad_i = np.zeros(env.n_trials) self.r_i = np.zeros(env.n_trials) self.thetas = np.zeros(self.n_trials) self.regret_i = np.zeros(env.n_trials) self.thetaregret = np.zeros(self.n_trials) self.a = np.ones(env.n_k) self.b = np.ones(env.n_k) self.theta = np.zeros(env.n_k) self.data = None self.reward = 0 self.total_reward = 0 self.k = 0 self.i = 0 self.n_samples = n_samples self.n_learning = n_learning self.e = e self.ep = np.random.uniform(0, 1, size=env.n_trials) self.exploit = (1 - e) def collect_data(self): self.data = pd.DataFrame(dict(ad=self.ad_i, reward=self.r_i, regret=self.regret_i)) 

Nachfolgend definieren wir 10 Optionen und Payback für jede. Die beste Option ist Option 9 mit einer Amortisation von 0,11%.

 variants = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9] payouts = [0.023, 0.03, 0.029, 0.001, 0.05, 0.06, 0.0234, 0.035, 0.01, 0.11] 

Um etwas aufzubauen, definieren wir auch die RandomSampler-Klasse. Diese Klasse wird als Basismodell benötigt. Er wählt einfach bei jedem Versuch rein zufällig eine Option und aktualisiert seine Parameter nicht.

 class RandomSampler(BaseSampler): def __init__(self, env): super().__init__(env) def choose_k(self): self.k = np.random.choice(self.variants) return self.k def update(self): # nothing to update #self.thetaregret[self.i] = self.thetaregret[self.i] #self.regret_i[self.i] = np.max(self.thetaregret) - self.theta[self.k] #self.thetas[self.i] = self.theta[self.k] self.thetaregret[self.i] = np.max(self.theta) - self.theta[self.k] self.a[self.k] += self.reward self.b[self.k] += 1 self.theta = self.a/self.b self.ad_i[self.i] = self.k self.r_i[self.i] = self.reward self.i += 1 

Andere Modelle haben die folgende Struktur. Alle haben select_k und Update-Methoden. select_k implementiert die Methode, mit der der Agent eine Option auswählt. update aktualisiert die Parameter des Agenten - diese Methode charakterisiert, wie sich die Fähigkeit des Agenten, die Option auszuwählen, ändert (mit RandomSampler ändert sich diese Fähigkeit in keiner Weise). Wir führen den Agenten in der Umgebung nach dem folgenden Muster aus.

 en0 = Environment(machines, payouts, n_trials=10000) rs = RandomSampler(env=en0) en0.run(agent=rs) 

Das Wesen des epsilon-gierigen Algorithmus ist wie folgt.

1. Wählen Sie zufällig k für n Versuche.
2. Bewerten Sie bei jedem Versuch für jede Option die Gewinne.
3. Nach allen n Versuchen:
4. Mit der Wahrscheinlichkeit 1 - e wählen Sie k mit der höchsten Verstärkung;
5. Mit der Wahrscheinlichkeit e wähle K zufällig.

Epsilon-gieriger Code:

 class eGreedy(BaseSampler): def __init__(self, env, n_learning, e): super().__init__(env, n_learning, e) def choose_k(self): # e% of the time take a random draw from machines # random k for n learning trials, then the machine with highest theta self.k = np.random.choice(self.variants) if self.i < self.n_learning else np.argmax(self.theta) # with 1 - e probability take a random sample (explore) otherwise exploit self.k = np.random.choice(self.variants) if self.ep[self.i] > self.exploit else self.k return self.k # every 100 trials update the successes # update the count of successes for the chosen machine def update(self): # update the probability of payout for each machine self.a[self.k] += self.reward self.b[self.k] += 1 self.theta = self.a/self.b #self.total_reward += self.reward #self.regret_i[self.i] = np.max(self.theta) - self.theta[self.k] #self.thetaregret[self.i] = self.thetaregret[self.i] self.thetas[self.i] = self.theta[self.k] self.thetaregret[self.i] = np.max(self.thetas) - self.theta[self.k] self.ad_i[self.i] = self.k self.r_i[self.i] = self.reward self.i += 1 

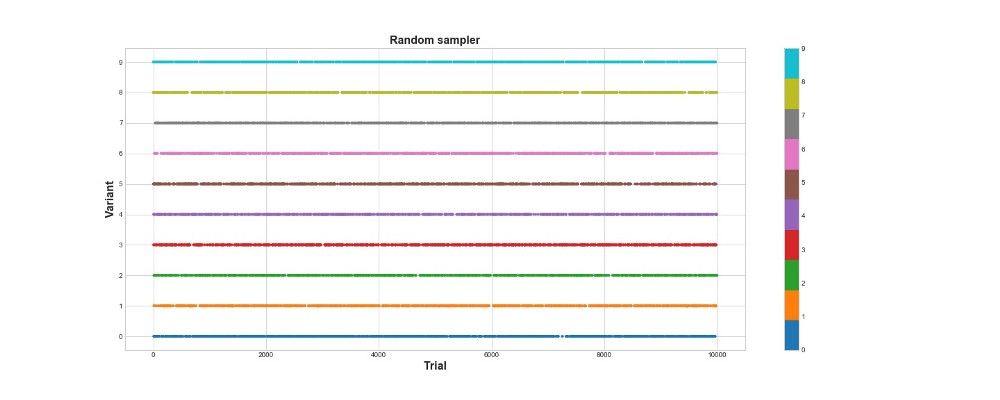
Unten in der Grafik sehen Sie die Ergebnisse einer rein zufälligen Stichprobe, dh es gibt hier kein Modell. Die Grafik zeigt, welche Auswahl der Algorithmus bei jedem Versuch getroffen hat, wenn es 10.000 Versuche gab. Der Algorithmus versucht nur, lernt aber nicht. Insgesamt erzielte er 418 Punkte.

Mal sehen, wie sich der epsilon-gierige Algorithmus in derselben Umgebung verhält. Führen Sie den Algorithmus für zehntausend Versuche mit e = 0,1 und n_learning = 500 aus (der Agent versucht einfach die ersten 500 Versuche, dann versucht er es mit der Wahrscheinlichkeit e = 0,1). Bewerten wir den Algorithmus anhand der Gesamtzahl der Punkte, die er in der Umgebung erzielt.

 en1 = Environment(machines, payouts, n_trials) eg = eGreedy(env=en1, n_learning=500, e=0.1) en1.run(agent=eg) 

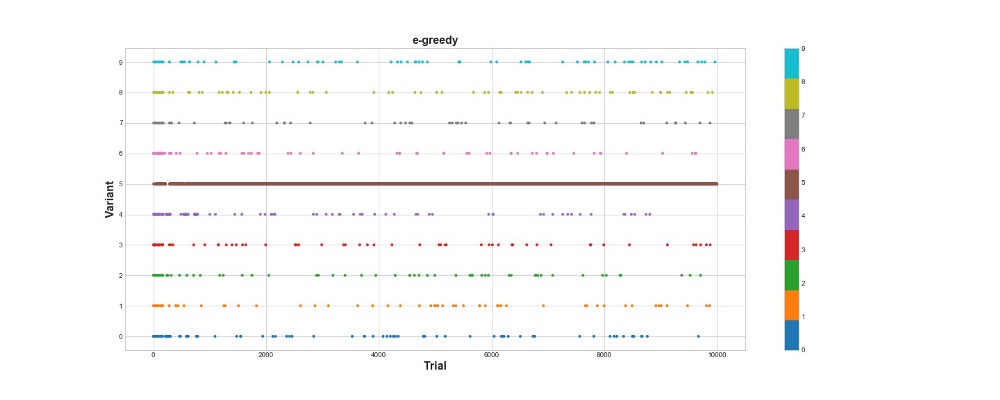
Der Epsilon-gierige Algorithmus erzielte 788 Punkte, fast zweimal besser als der Zufallsalgorithmus - super! Das zweite Diagramm erklärt diesen Algorithmus ziemlich gut. Wir sehen, dass für die ersten 500 Schritte die Aktionen ungefähr gleichmäßig verteilt sind und K zufällig ausgewählt wird. Dann beginnt es jedoch, Option 5 stark auszunutzen - dies ist eine ziemlich starke Option, aber nicht die beste. Wir sehen auch, dass der Agent immer noch 10% der Zeit zufällig auswählt.

Das ist ziemlich cool - wir haben nur ein paar Codezeilen geschrieben und jetzt haben wir bereits einen ziemlich leistungsfähigen Algorithmus, der den Raum der Optionen erkunden und Entscheidungen treffen kann, die nahezu optimal sind. Andererseits fand der Algorithmus nicht die beste Option. Ja, wir können die Anzahl der Lernschritte erhöhen, aber auf diese Weise verbringen wir noch mehr Zeit mit einer zufälligen Suche, was das Endergebnis weiter verschlechtert. Außerdem wird standardmäßig Zufälligkeit in diesen Prozess eingenäht - der beste Algorithmus wird möglicherweise nicht gefunden.

Später werde ich jeden der Algorithmen viele Male ausführen, damit wir sie relativ zueinander vergleichen können. Aber jetzt schauen wir uns die Thompson-Probenahme an und testen sie in derselben Umgebung.

Thompson-Probenahme

Die Thompson-Abtastung unterscheidet sich grundlegend vom epsilon-gierigen Algorithmus durch drei Hauptpunkte:

1. Es ist nicht gierig.
2. Es macht Versuche auf raffiniertere Weise.
3. Es ist Bayesianisch.

Der Hauptpunkt ist Absatz 3, daraus folgen die Absätze 1 und 2.

Das Wesentliche des Algorithmus ist:

1. Stellen Sie die anfängliche Beta-Verteilung für die Rückzahlung jeder Option zwischen 0 und 1 ein.
2. Probieren Sie die Optionen aus dieser Verteilung aus und wählen Sie den maximalen Theta-Parameter aus.
3. Wählen Sie die Option k, die dem größten Theta zugeordnet ist.
4. Zeigen Sie an, wie viele Punkte erzielt wurden, und aktualisieren Sie die Verteilungsparameter.

Lesen Sie hier mehr über die Beta-Distribution.
Und über seine Verwendung in Python - hier .

Algorithmuscode:

  class ThompsonSampler(BaseSampler): def __init__(self, env): super().__init__(env) def choose_k(self): # sample from posterior (this is the thompson sampling approach) # this leads to more exploration because machines with > uncertainty can then be selected as the machine self.theta = np.random.beta(self.a, self.b) # select machine with highest posterior p of payout self.k = self.variants[np.argmax(self.theta)] #self.k = np.argmax(self.a/(self.a + self.b)) return self.k def update(self): #update dist (a, b) = (a, b) + (r, 1 - r) self.a[self.k] += self.reward self.b[self.k] += 1 - self.reward # ie only increment b when it's a swing and a miss. 1 - 0 = 1, 1 - 1 = 0 #self.thetaregret[self.i] = self.thetaregret[self.i] #self.regret_i[self.i] = np.max(self.theta) - self.theta[self.k] self.thetas[self.i] = self.theta[self.k] self.thetaregret[self.i] = np.max(self.thetas) - self.theta[self.k] self.ad_i[self.i] = self.k self.r_i[self.i] = self.reward self.i += 1 

Die formale Notation des Algorithmus sieht so aus.

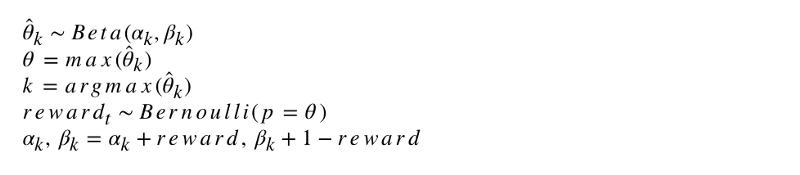
Programmieren wir diesen Algorithmus. Wie andere Agenten erbt ThompsonSampler von BaseSampler und definiert seine eigenen Methoden select_k und update. Starten Sie jetzt unseren neuen Agenten.

  en2 = Environment(machines, payouts, n_trials) tsa = ThompsonSampler(env=en2) en2.run(agent=tsa) 

Wie Sie sehen können, erzielte er mehr als der epsilon-gierige Algorithmus. Großartig! Schauen wir uns das Diagramm der Auswahl der Versuche an. Darauf sind zwei interessante Dinge zu sehen. Erstens hat der Agent die beste Option (Option 9) korrekt erkannt und in vollem Umfang genutzt. Zweitens verwendete der Agent andere Optionen, jedoch auf schwierigere Weise - nach etwa 1000 Versuchen verwendete der Agent neben der Hauptoption hauptsächlich die leistungsstärksten Optionen unter den anderen. Mit anderen Worten, er wählte nicht zufällig, sondern kompetenter.

Warum funktioniert das? Es ist ganz einfach: Die Unsicherheit in der posterioren Verteilung des erwarteten Nutzens für jede Option bedeutet, dass jede Option mit einer Wahrscheinlichkeit ausgewählt wird, die ungefähr proportional zu ihrer Form ist und durch die Alpha- und Beta-Parameter bestimmt wird. Mit anderen Worten, bei jedem Versuch löst die Thompson-Stichprobe die Option entsprechend der posterioren Wahrscheinlichkeit aus, dass sie den maximalen Nutzen hat. Grob gesagt entscheidet der Agent anhand der Verteilungsinformationen über die Unsicherheit, wann die Umgebung untersucht und wann die Informationen verwendet werden sollen. Beispielsweise kann eine schwache Option mit hoher posteriorer Unsicherheit für diesen Versuch am meisten zahlen. Bei den meisten Versuchen ist jedoch die Wahrscheinlichkeit einer Auswahl umso größer, je stärker die posteriore Verteilung ist, je größer der Durchschnitt und je geringer die Standardabweichung ist.

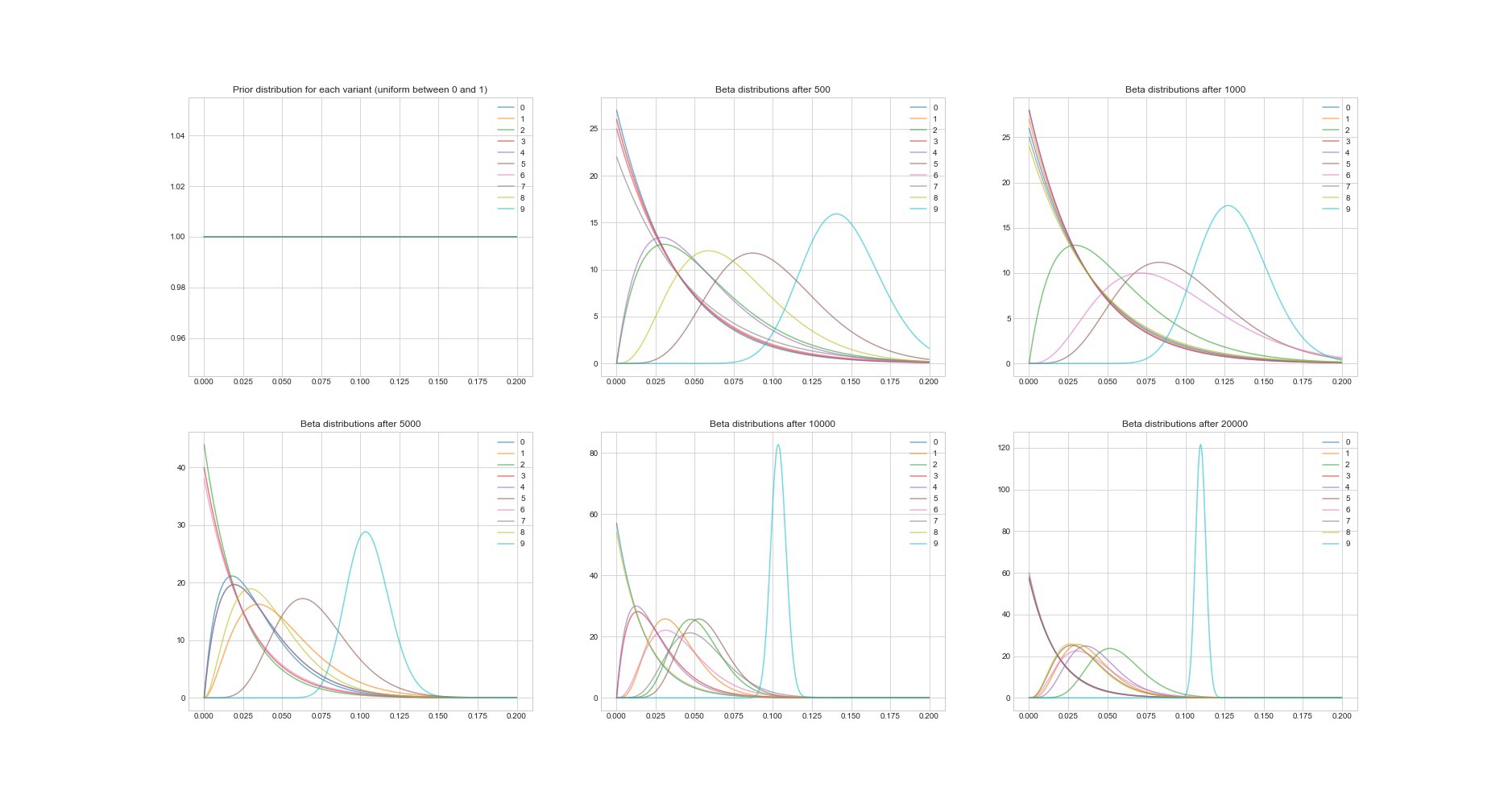
Eine weitere bemerkenswerte Eigenschaft des Thompson-Algorithmus: Da es sich um einen Bayes'schen Algorithmus handelt, können wir die Unsicherheit in der Amortisationsschätzung für jede Option anhand ihrer Parameter abschätzen. Die folgende Grafik zeigt die posterioren Verteilungen an 6 verschiedenen Punkten und in 20.000 Versuchen. Sie sehen, wie Verteilungen allmählich zur Option mit der besten Amortisation konvergieren.

Vergleichen Sie nun alle 3 Agenten in 100 Simulationen. 1 Simulation ist ein Agentenstart bei 10.000 Versuchen.

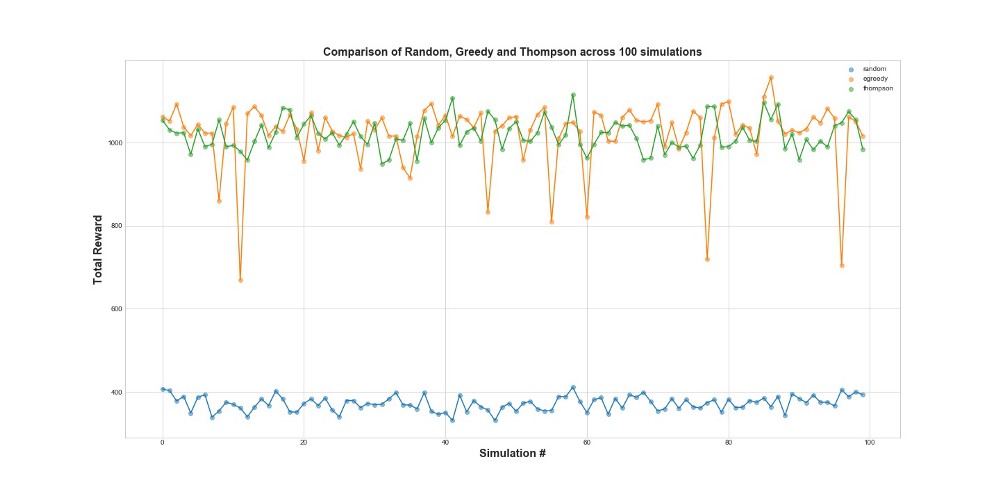
Wie Sie in der Grafik sehen können, funktionieren sowohl die epsilon-gierige Strategie als auch die Thompson-Stichprobe viel besser als die Zufallsstichprobe. Sie werden überrascht sein, dass die epsilon-gierige Strategie und die Thompson-Stichprobe hinsichtlich ihrer Leistung tatsächlich vergleichbar sind. Eine Epsilon-gierige Strategie kann sehr effektiv sein, ist jedoch riskanter, da sie bei einer suboptimalen Option hängen bleiben kann - dies ist an den Fehlern in der Grafik zu erkennen. Aber Thompson Sampling kann nicht, weil es die Auswahl im Bereich der Optionen auf komplexere Weise trifft.

Bedauern

Eine andere Möglichkeit, um zu bewerten, wie gut der Algorithmus funktioniert, besteht darin, das Bedauern zu bewerten. Grob gesagt ist es umso besser, je kleiner es im Verhältnis zu den bereits ergriffenen Maßnahmen ist. Unten finden Sie eine grafische Darstellung des gesamten Bedauerns und des Bedauerns für den Fehler. Noch einmal - je weniger Bedauern, desto besser.

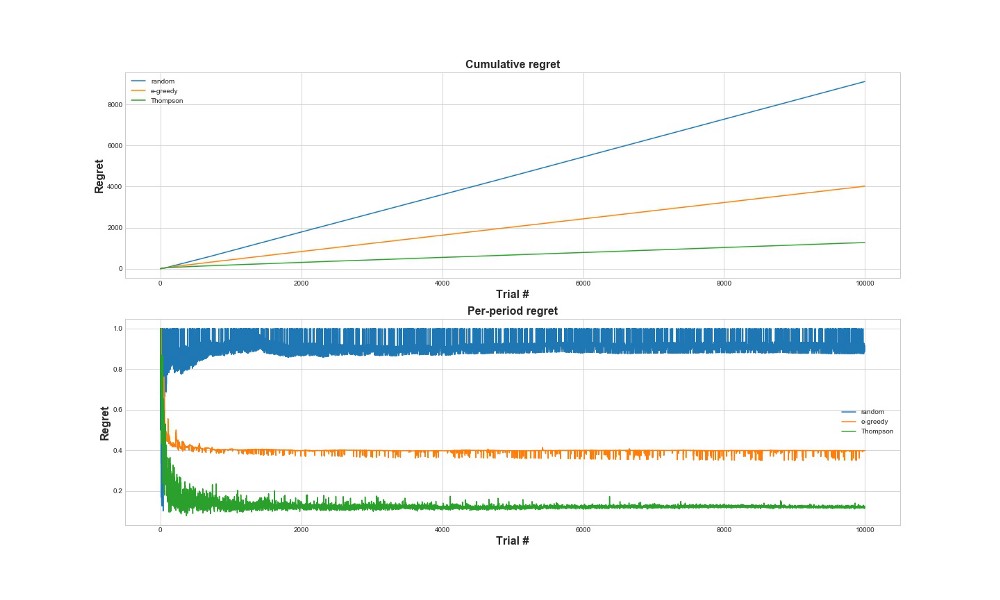
In der oberen Grafik sehen wir das totale Bedauern und in der unteren den Versuch. Wie aus den Grafiken ersichtlich ist, konvergiert die Thompson-Stichprobe viel schneller zu minimalem Bedauern als die epsilon-gierige Strategie. Und es konvergiert auf eine niedrigere Ebene. Bei der Thompson-Stichprobe bereut der Agent weniger, da er die beste Option besser erkennen und die vielversprechendsten Optionen besser ausprobieren kann. Die Thompson-Stichprobe eignet sich daher besonders für fortgeschrittenere Anwendungsfälle wie statistische Modelle oder neuronale Netze zur Auswahl von k.

Schlussfolgerungen

Dies ist ein ziemlich langer technischer Beitrag. Zusammenfassend können wir ziemlich ausgefeilte Stichprobenmethoden verwenden, wenn wir viele Optionen haben, die wir in Echtzeit testen möchten. Eine der sehr guten Eigenschaften der Thompson-Probenahme ist, dass sie die Nutzung und Erkundung auf ziemlich knifflige Weise in Einklang bringt. Das heißt, wir können ihn die Verteilung der Lösungsoptionen in Echtzeit optimieren lassen. Dies sind coole Algorithmen, die für ein Unternehmen nützlicher sein sollten als A / B-Tests.

Wichtig! Thompson-Stichproben bedeuten nicht, dass Sie keine A / B-Tests durchführen müssen. Normalerweise finden sie zuerst mit seiner Hilfe die besten Optionen und führen dann bereits A / B-Tests durch.