 Ein vollständiger Durchgang zum maschinellen Lernen in Python: Teil Zwei
Ein vollständiger Durchgang zum maschinellen Lernen in Python: Teil ZweiDas Zusammenstellen aller Teile eines maschinellen Lernprojekts kann schwierig sein. In dieser Artikelserie werden wir alle Phasen der Implementierung des maschinellen Lernprozesses anhand realer Daten durchlaufen und herausfinden, wie die verschiedenen Techniken miteinander kombiniert werden.
Im
ersten Artikel haben wir die Daten bereinigt und strukturiert, eine explorative Analyse durchgeführt, eine Reihe von Attributen zur Verwendung im Modell gesammelt und eine Basis für die Bewertung der Ergebnisse festgelegt. Mithilfe dieses Artikels lernen wir, wie Sie in Python implementieren und mehrere Modelle für maschinelles Lernen vergleichen, eine hyperparametrische Optimierung durchführen, um das beste Modell zu optimieren, und die Leistung des endgültigen Modells anhand eines Testdatensatzes bewerten.
Der gesamte Projektcode befindet sich
auf GitHub , und
hier ist das zweite Notizbuch, das sich auf den aktuellen Artikel bezieht. Sie können den Code beliebig verwenden und ändern!
Modellbewertung und -auswahl
Anmerkung: Wir arbeiten an einer kontrollierten Regressionsaufgabe, bei der mithilfe von
Energieinformationen aus Gebäuden in New York ein Modell erstellt wird, das vorhersagt, welchen
Energy Star Score ein bestimmtes Gebäude erhalten wird. Wir sind sowohl an der Genauigkeit der Prognose als auch an der Interpretierbarkeit des Modells interessiert.
Heute können Sie aus den
vielen verfügbaren Modellen für maschinelles Lernen auswählen, und diese Fülle kann einschüchternd sein. Natürlich gibt es im Netzwerk
vergleichende Bewertungen , die Ihnen bei der Auswahl eines Algorithmus helfen, aber ich ziehe es vor, einige davon auszuprobieren und herauszufinden, welcher besser ist. Zum größten Teil basiert maschinelles Lernen eher auf
empirischen als auf theoretischen Ergebnissen , und es ist fast
unmöglich, im Voraus zu verstehen, welches Modell genauer ist .
Es wird allgemein empfohlen, mit einfachen, interpretierbaren Modellen wie der linearen Regression zu beginnen. Wenn die Ergebnisse nicht zufriedenstellend sind, fahren Sie mit komplexeren, aber normalerweise genaueren Methoden fort. Diese Grafik (sehr anti-wissenschaftlich) zeigt die Beziehung zwischen der Genauigkeit und Interpretierbarkeit einiger Algorithmen:
 Interpretierbarkeit und Genauigkeit ( Quelle ).
Interpretierbarkeit und Genauigkeit ( Quelle ).Wir werden fünf Modelle mit unterschiedlichem Komplexitätsgrad bewerten:
- Lineare Regression.
- Die Methode der k-nächsten Nachbarn.
- "Zufälliger Wald."
- Gradientenverstärkung.
- Methode der Unterstützungsvektoren.
Wir werden nicht den theoretischen Apparat dieser Modelle betrachten, sondern ihre Implementierung. Wenn Sie sich für Theorie interessieren,
lesen Sie eine Einführung in das statistische Lernen (kostenlos erhältlich) oder das
praktische maschinelle Lernen mit Scikit-Learn und TensorFlow . In beiden Büchern wird die Theorie perfekt erklärt und die Wirksamkeit der Verwendung der genannten Methoden in den Sprachen R bzw. Python gezeigt.
Geben Sie die fehlenden Werte ein
Obwohl wir beim Löschen der Daten die Spalten verworfen haben, in denen mehr als die Hälfte der Werte fehlen, haben wir immer noch viele Werte. Modelle für maschinelles Lernen können nicht mit fehlenden Daten arbeiten, daher müssen wir sie
ausfüllen .
Zuerst betrachten wir die Daten und erinnern uns, wie sie aussehen:
import pandas as pd import numpy as np
Jeder
NaN Wert ist ein fehlender Datensatz in den Daten.
Sie können sie auf verschiedene Arten füllen , und wir verwenden die relativ einfache Median-Imputationsmethode, bei der die fehlenden Daten durch die Durchschnittswerte für die entsprechenden Spalten ersetzt werden.
Im folgenden Code erstellen wir ein
Scikit-Learn Imputer-
Imputer mit einer Medianstrategie. Dann trainieren wir es mit den Trainingsdaten (mit
imputer.fit ) und wenden es an, um die fehlenden Werte in den Trainings- und Testsätzen (mit
imputer.transform )
imputer.transform . Das heißt, die Datensätze, die in den
Testdaten fehlen, werden mit dem entsprechenden Medianwert aus den
Trainingsdaten gefüllt.
Wir führen das Füllen durch und trainieren das Modell nicht so, wie es ist, um das Problem des
Verlusts von Testdaten zu vermeiden, wenn Informationen aus dem Testdatensatz in das Training einfließen.
Jetzt sind alle Werte gefüllt, es gibt keine Lücken.
Feature-Skalierung
Die Skalierung ist der allgemeine Prozess zum Ändern des Bereichs eines Merkmals.
Dies ist ein notwendiger Schritt , da Vorzeichen in verschiedenen Einheiten gemessen werden, was bedeutet, dass sie unterschiedliche Bereiche abdecken. Dies verzerrt die Ergebnisse von Algorithmen wie
der Support-Vektor- Methode und der k-Nearest-Neighbour-Methode, die die Abstände zwischen den Messungen berücksichtigen, erheblich. Durch Skalierung können Sie dies vermeiden. Obwohl Methoden wie
lineare Regression und „Random Forest“ keine Skalierung von Features erfordern, ist es besser, diesen Schritt beim Vergleich mehrerer Algorithmen nicht zu vernachlässigen.
Wir skalieren mit jedem Attribut auf einen Bereich von 0 bis 1. Wir nehmen alle Werte des Attributs, wählen das Minimum aus und dividieren es durch die Differenz zwischen Maximum und Minimum (Bereich). Diese Skalierungsmethode wird oft als
Normalisierung bezeichnet, und der andere Hauptweg ist die Standardisierung .
Dieser Prozess ist einfach manuell zu implementieren, daher verwenden wir das
MinMaxScaler Objekt von Scikit-Learn. Der Code für diese Methode ist identisch mit dem Code zum Ausfüllen der fehlenden Werte. Anstelle des Einfügens wird nur die Skalierung verwendet. Denken Sie daran, dass wir das Modell nur im Trainingssatz lernen und dann alle Daten transformieren.
Jetzt hat jedes Attribut einen Mindestwert von 0 und einen Höchstwert von 1. Das Ausfüllen der fehlenden Werte und die Skalierung der Attribute - diese beiden Stufen werden in fast jedem maschinellen Lernprozess benötigt.
Wir implementieren maschinelle Lernmodelle in Scikit-Learn
Nach all den Vorarbeiten ist das Erstellen, Trainieren und Ausführen von Modellen relativ einfach. Wir werden die
Scikit-Learn- Bibliothek in Python verwenden, die wunderschön dokumentiert ist und über eine ausgefeilte Syntax zum
Erstellen von Modellen verfügt. Indem Sie lernen, wie Sie in Scikit-Learn ein Modell erstellen, können Sie schnell alle Arten von Algorithmen implementieren.
Wir werden den Prozess der Erstellung, des Trainings (
.fit ) und des Testens (
.predict ) mithilfe der Gradientenverstärkung
.predict :
from sklearn.ensemble import GradientBoostingRegressor
Nur eine Codezeile zum Erstellen, Trainieren und Testen. Um andere Modelle zu erstellen, verwenden wir dieselbe Syntax und ändern nur den Namen des Algorithmus.

Um Modelle objektiv zu bewerten, haben wir den Basispegel anhand des Medianwerts des Ziels berechnet und 24,5 erhalten. Die Ergebnisse waren viel besser, sodass unser Problem durch maschinelles Lernen gelöst werden kann.
In unserem Fall erwies sich die
Gradientenverstärkung (MAE = 10.013) als etwas besser als die "zufällige Gesamtstruktur" (10.014 MAE). Obwohl diese Ergebnisse nicht als ganz ehrlich angesehen werden können, verwenden wir für Hyperparameter meistens die Standardwerte. Die Wirksamkeit der Modelle hängt stark von diesen Einstellungen ab,
insbesondere bei der Support-Vektor-Methode . Basierend auf diesen Ergebnissen werden wir jedoch die Gradientenverstärkung wählen und beginnen, sie zu optimieren.
Hyperparametrische Modelloptimierung
Nachdem Sie ein Modell ausgewählt haben, können Sie es durch Anpassen der Hyperparameter für die zu lösende Aufgabe optimieren.
Aber lassen Sie uns zunächst verstehen,
was Hyperparameter sind und wie sie sich von gewöhnlichen Parametern unterscheiden .
- Die Hyperparameter des Modells können als Einstellungen des Algorithmus betrachtet werden, die wir vor Beginn des Trainings festgelegt haben. Beispielsweise ist der Hyperparameter die Anzahl der Bäume in der "zufälligen Gesamtstruktur" oder die Anzahl der Nachbarn in der Methode der k-nächsten Nachbarn.
- Modellparameter - was sie während des Trainings lernt, zum Beispiel Gewichte in linearer Regression.
Durch die Steuerung des Hyperparameters beeinflussen wir die Ergebnisse des Modells und verändern das Gleichgewicht zwischen
Untererziehung und Umschulung . Unter Lernen versteht man eine Situation, in der das Modell nicht komplex genug ist (es hat zu wenig Freiheitsgrade), um die Entsprechung von Zeichen und Zielen zu untersuchen. Ein untertrainiertes Modell weist eine
hohe Vorspannung auf, die durch Komplikation des Modells korrigiert werden kann.
Umschulung ist eine Situation, in der sich das Modell im Wesentlichen an die Trainingsdaten erinnert. Das umgeschulte Modell weist eine
hohe Varianz auf, die angepasst werden kann, indem die Komplexität des Modells durch Regularisierung begrenzt wird. Sowohl unter- als auch umgeschulte Modelle können die Testdaten nicht gut verallgemeinern.
Die Schwierigkeit bei der Auswahl der richtigen Hyperparameter besteht darin, dass für jede Aufgabe ein eindeutiger optimaler Satz vorhanden ist. Daher können Sie die besten Einstellungen nur auswählen, indem Sie verschiedene Kombinationen für das neue Dataset ausprobieren. Glücklicherweise verfügt Scikit-Learn über eine Reihe von Methoden, mit denen Sie Hyperparameter effektiv bewerten können. Darüber hinaus versuchen Projekte wie
TPOT , die Suche nach Hyperparametern mithilfe von Ansätzen wie der
genetischen Programmierung zu optimieren. In diesem Artikel beschränken wir uns auf die Verwendung von Scikit-Learn.
Überprüfen Sie die zufällige Suche
Lassen Sie uns eine Hyperparameter-Optimierungsmethode implementieren, die als zufällige Kreuzvalidierungssuchen bezeichnet wird:
- Zufallssuche - eine Technik zur Auswahl von Hyperparametern. Wir definieren ein Raster und wählen dann zufällig verschiedene Kombinationen daraus aus, im Gegensatz zur Rastersuche, bei der wir jede Kombination nacheinander ausprobieren. Die Zufallssuche funktioniert übrigens fast genauso gut wie die Rastersuche , ist aber viel schneller.
- Durch Gegenprüfung kann die ausgewählte Kombination von Hyperparametern bewertet werden. Anstatt die Daten in Trainings- und Testsätze aufzuteilen, wodurch die für das Training verfügbare Datenmenge reduziert wird, verwenden wir die K-Block-Kreuzvalidierung (K-Fold Cross Validation). Dazu teilen wir die Trainingsdaten in k Blöcke auf und führen dann den iterativen Prozess aus, bei dem wir zuerst das Modell auf k-1 Blöcken trainieren und dann das Ergebnis vergleichen, wenn wir auf dem k-ten Block lernen. Wir werden den Vorgang k-mal wiederholen und am Ende den durchschnittlichen Fehlerwert für jede Iteration erhalten. Dies wird die endgültige Bewertung sein.
Hier ist eine grafische Darstellung der Kreuzvalidierung von k-Blöcken bei k = 5:

Der gesamte zufällige Suchprozess für die Kreuzvalidierung sieht folgendermaßen aus:
- Wir setzen ein Gitter von Hyperparametern.
- Wählen Sie zufällig eine Kombination von Hyperparametern aus.
- Erstellen Sie mit dieser Kombination ein Modell.
- Wir bewerten das Ergebnis des Modells mithilfe der K-Block-Kreuzvalidierung.
- Wir entscheiden, welche Hyperparameter das beste Ergebnis liefern.
Natürlich geschieht dies alles nicht manuell, sondern mit
RandomizedSearchCV von Scikit-Learn!
Wir werden ein Gradienten-Boost-basiertes Regressionsmodell verwenden. Dies ist eine kollektive Methode, dh das Modell besteht aus zahlreichen „schwachen Lernenden“, in diesem Fall aus separaten Entscheidungsbäumen. Wenn die Schüler in parallelen
Algorithmen wie „Random Forest“ lernen und dann das Vorhersageergebnis durch Abstimmung ausgewählt wird, lernen die Schüler in
Boosting-Algorithmen wie Gradient Boosting nacheinander und jeder von ihnen „konzentriert“ sich auf die Fehler seiner Vorgänger.
In den letzten Jahren sind Boosting-Algorithmen populär geworden und gewinnen häufig bei Wettbewerben für maschinelles Lernen.
Gradient Boosting ist eine der Implementierungen, bei denen Gradient Descent verwendet wird, um die Kosten der Funktion zu minimieren. Die Implementierung der Gradientenverstärkung in Scikit-Learn wird als nicht so effektiv angesehen wie in anderen Bibliotheken, beispielsweise in
XGBoost , funktioniert jedoch gut bei kleinen Datensätzen und liefert ziemlich genaue Vorhersagen.
Zurück zur hyperparametrischen Einstellung
Bei der Regression mit Gradientenverstärkung müssen viele Hyperparameter konfiguriert werden. Einzelheiten finden Sie in der Scikit-Learn-Dokumentation. Wir werden optimieren:
loss : Minimierung der Verlustfunktion;n_estimators : Anzahl der verwendeten schwachen Entscheidungsbäume (Entscheidungsbäume);max_depth : maximale Tiefe jedes Entscheidungsbaums;min_samples_leaf : Die Mindestanzahl von Beispielen, die sich im Blattknoten des Entscheidungsbaums befinden sollten.min_samples_split : Die Mindestanzahl von Beispielen, die zum min_samples_split des Entscheidungsbaumknotens erforderlich sind.max_features : Die maximale Anzahl von Features, die zum Trennen von Knoten verwendet werden.
Ich bin mir nicht sicher, ob jemand wirklich versteht, wie das alles funktioniert, und der einzige Weg, die beste Kombination zu finden, besteht darin, verschiedene Optionen auszuprobieren.
In diesem Code erstellen wir ein Raster von Hyperparametern, erstellen dann ein
RandomizedSearchCV Objekt und suchen mithilfe der 4-Block-Kreuzvalidierung nach 25 verschiedenen Kombinationen von Hyperparametern:
Sie können diese Ergebnisse für eine Rastersuche verwenden, indem Sie Parameter für das Raster auswählen, die nahe an diesen optimalen Werten liegen. Eine weitere Abstimmung dürfte das Modell jedoch nicht wesentlich verbessern. Es gibt eine allgemeine Regel: Die kompetente Konstruktion von Merkmalen hat einen viel größeren Einfluss auf die Genauigkeit des Modells als die teuerste Hyperparametereinstellung. Dies ist das
Gesetz zur Verringerung der Rentabilität in Bezug auf maschinelles Lernen : Das Entwerfen von Attributen bietet die höchste Rendite, und hyperparametrisches Tuning bringt nur bescheidene Vorteile.
Um die Anzahl der Schätzer (Entscheidungsbäume) zu ändern und gleichzeitig die Werte anderer Hyperparameter beizubehalten, kann ein Experiment durchgeführt werden, das die Rolle dieser Einstellung demonstriert. Die Implementierung ist
hier angegeben , aber hier ist das Ergebnis:
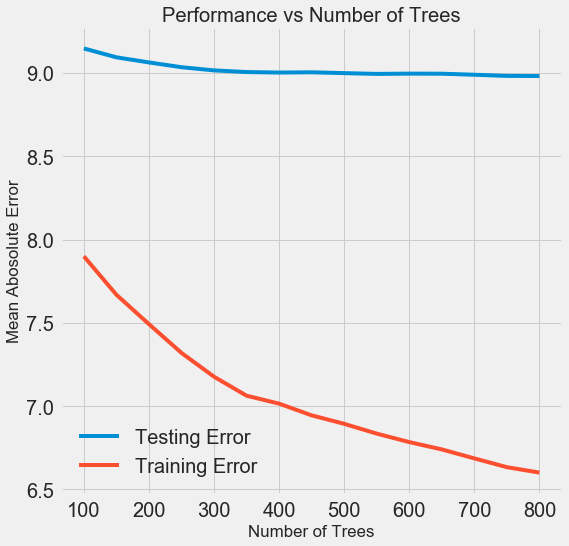
Mit zunehmender Anzahl der vom Modell verwendeten Bäume nimmt die Fehlerquote beim Training und Testen ab. Lernfehler nehmen jedoch viel schneller ab, und infolgedessen wird das Modell umgeschult: Es zeigt hervorragende Ergebnisse bei Trainingsdaten, funktioniert jedoch schlechter bei Testdaten.
Bei Testdaten nimmt die Genauigkeit immer ab (da das Modell die richtigen Antworten für den Trainingsdatensatz sieht), aber ein signifikanter Rückgang
weist auf eine Umschulung hin . Dieses Problem kann gelöst werden, indem die Menge der Trainingsdaten erhöht oder
die Komplexität des Modells mithilfe von Hyperparametern verringert wird . Hier werden wir nicht auf Hyperparameter eingehen, aber ich empfehle Ihnen, immer auf das Problem der Umschulung zu achten.
Für unser endgültiges Modell werden 800 Bewerter herangezogen, da dies die niedrigste Fehlerquote bei der Kreuzvalidierung ergibt. Testen Sie jetzt das Modell!
Bewertung anhand von Testdaten
Als Verantwortliche haben wir dafür gesorgt, dass unser Modell während des Trainings in keiner Weise Zugang zu Testdaten erhielt. Daher können
wir die Genauigkeit bei der Arbeit mit Testdaten als Modellqualitätsindikator
verwenden, wenn diese für reale Aufgaben zugelassen sind.
Wir geben die Modelltestdaten ein und berechnen den Fehler. Hier ist ein Vergleich der Ergebnisse des Standardalgorithmus zur Erhöhung des Gradienten und unseres benutzerdefinierten Modells:
Durch hyperparametrische Abstimmung konnte die Modellgenauigkeit um etwa 10% verbessert werden. Je nach Situation kann dies eine erhebliche Verbesserung sein, die jedoch viel Zeit in Anspruch nimmt.
Sie können die Trainingszeit für beide Modelle mit dem
%timeit magic
%timeit in Jupyter Notebooks vergleichen. Messen Sie zunächst die Standarddauer des Modells:
%%timeit -n 1 -r 5 default_model.fit(X, y) 1.09 s ± 153 ms per loop (mean ± std. dev. of 5 runs, 1 loop each)
Eine Sekunde zum Lernen ist sehr anständig. Aber das getunte Modell ist nicht so schnell:
%%timeit -n 1 -r 5 final_model.fit(X, y) 12.1 s ± 1.33 s per loop (mean ± std. dev. of 5 runs, 1 loop each)
Diese Situation verdeutlicht den grundlegenden Aspekt des maschinellen Lernens:
Es geht um Kompromisse . Es ist ständig notwendig, ein Gleichgewicht zwischen Genauigkeit und Interpretierbarkeit, zwischen
Verschiebung und Streuung , zwischen Genauigkeit und Betriebszeit usw. zu wählen. Die richtige Kombination wird vollständig von der spezifischen Aufgabe bestimmt. In unserem Fall ist eine 12-fache Verlängerung der Arbeitsdauer relativ gesehen groß, aber absolut gesehen unbedeutend.
Wir haben die endgültigen Prognoseergebnisse erhalten. Analysieren wir sie nun und stellen fest, ob es erkennbare Abweichungen gibt. Links ist ein Diagramm der Dichte der vorhergesagten und realen Werte, rechts ein Histogramm des Fehlers:
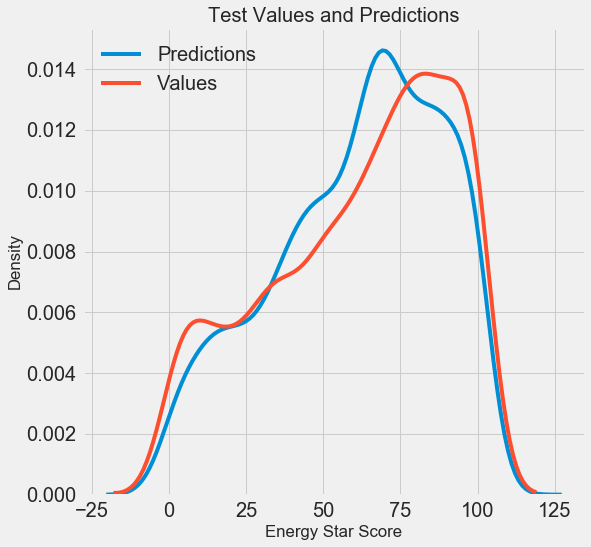

Die Vorhersage des Modells wiederholt die Verteilung der realen Werte gut, während sich der Dichtepeak in den Trainingsdaten näher am Medianwert (66) befindet als am realen Dichtepeak (etwa 100). Fehler haben eine fast normale Verteilung, obwohl es mehrere große negative Werte gibt, wenn sich die Modellprognose stark von den realen Daten unterscheidet. Im nächsten Artikel werden wir uns die Interpretation der Ergebnisse genauer ansehen.
Fazit
In diesem Artikel haben wir verschiedene Phasen der Lösung des Problems des maschinellen Lernens untersucht:
- Fehlende Werte und Skalierungsfunktionen ausfüllen.
- Auswertung und Vergleich der Ergebnisse mehrerer Modelle.
- Hyperparametrische Abstimmung mit zufälliger Rastersuche und Kreuzvalidierung.
- Bewertung des besten Modells anhand von Testdaten.
Die Ergebnisse zeigen, dass wir maschinelles Lernen verwenden können, um den Energy Star Score basierend auf verfügbaren Statistiken vorherzusagen. Mit Hilfe der Gradientenverstärkung wurde ein Fehler von 9,1 bei den Testdaten erreicht. Hyperparametrisches Tuning kann die Ergebnisse erheblich verbessern, jedoch auf Kosten einer signifikanten Verlangsamung. Dies ist einer von vielen Kompromissen, die beim maschinellen Lernen berücksichtigt werden müssen.
Im nächsten Artikel werden wir versuchen herauszufinden, wie unser Modell funktioniert. Wir werden uns auch die Hauptfaktoren ansehen, die den Energy Star Score beeinflussen. Wenn wir wissen, dass das Modell genau ist, werden wir versuchen zu verstehen, warum es dies vorhersagt und was uns dies über das Problem selbst sagt.