Symbolische Lösung linearer Differentialgleichungen und -systeme durch die Laplace-Transformationsmethode mit SymPy

Die Implementierung von Algorithmen in Python mithilfe symbolischer Berechnungen ist sehr praktisch, um Probleme der mathematischen Modellierung von Objekten zu lösen, die durch Differentialgleichungen definiert sind. Um solche Gleichungen zu lösen, werden häufig Laplace-Transformationen verwendet, die es vereinfacht ausgedrückt ermöglichen, das Problem auf die Lösung einfacher algebraischer Gleichungen zu reduzieren.

In dieser Veröffentlichung schlage ich vor, die Funktionen der direkten und inversen Laplace-Transformationen aus der SymPy-Bibliothek zu berücksichtigen, mit denen Sie die Laplace-Methode verwenden können, um Differentialgleichungen und Systeme mit Python zu lösen.

Die Laplace-Methode selbst und ihre Vorteile bei der Lösung linearer Differentialgleichungen und -systeme werden in der Literatur ausführlich behandelt, beispielsweise in der populären Veröffentlichung [1]. In dem Buch wird die Laplace-Methode zur Implementierung in lizenzierten Softwarepaketen Mathematica, Maple und MATLAB (was den Kauf dieser Software durch eine Bildungseinrichtung impliziert) anhand ausgewählter Beispiele des Autors vorgestellt.

Heute werden wir versuchen, kein separates Beispiel für die Lösung eines Lernproblems mit Python zu betrachten, sondern eine allgemeine Methode zur Lösung linearer Differentialgleichungen und -systeme unter Verwendung der Funktionen direkter und inverser Laplace-Transformationen. Gleichzeitig sparen wir einen Lernmoment: Die linke Seite der linearen Differentialgleichung mit Cauchy-Bedingungen wird vom Schüler selbst gebildet, und der Routineteil der Aufgabe, der in der direkten Laplace-Transformation der rechten Seite der Gleichung besteht, wird mit der Funktion laplace_transform () ausgeführt .

Die Geschichte der Urheberschaft der Laplace-Transformation

Laplace-Transformationen (Laplace-Bilder) haben eine interessante Geschichte. Zum ersten Mal erschien das Integral in der Definition der Laplace-Transformation in einem der Werke von L. Euler. In der Mathematik ist es jedoch allgemein anerkannt, eine Methodik oder einen Satz den Namen des Mathematikers zu nennen, der ihn nach Euler entdeckt hat. Andernfalls würde es mehrere hundert verschiedene Euler-Sätze geben.

In diesem Fall war der nächste nach Euler der französische Mathematiker Pierre Simon de Laplace (Pierre Simon de Laplace (1749-1827)). Er hat solche Integrale in seiner Arbeit zur Wahrscheinlichkeitstheorie verwendet. Laplace selbst hat die sogenannten "Operationsmethoden" nicht angewendet, um Lösungen von Differentialgleichungen zu finden, die auf Laplace-Transformationen (Laplace-Bildern) basieren. Diese Methoden wurden tatsächlich von praktischen Ingenieuren entdeckt und populär gemacht, insbesondere vom englischen Elektrotechniker Oliver Heaviside (1850-1925). Lange bevor die Gültigkeit dieser Methoden rigoros bewiesen wurde, wurde die Operationsrechnung erfolgreich und weit verbreitet eingesetzt, obwohl ihre Legitimität bereits zu Beginn des 20. Jahrhunderts weitgehend in Frage gestellt wurde und es eine sehr heftige Debatte zu diesem Thema gab.

Funktionen der direkten und inversen Laplace-Transformation

1. Laplace-Direkttransformationsfunktion:
   sympy.integrals.transforms. laplace_transform (t, s, ** Hinweise).
   Die Funktion laplace_transform () führt die Laplace-Transformationen der Funktion f (t) der realen Variablen in die Funktion F (s) der komplexen Variablen durch, so dass:
   

   $$

   $$F (s) = \ int_ {0} ^ {∞} f (t) e ^ {- st} dt.$$
   
   Diese Funktion gibt (F, a, cond) zurück , wobei F (s) die Laplace-Transformation der Funktion f (t) ist , a <Re (s) die Halbebene ist, in der F (s) definiert ist, und cond Hilfsbedingungen für die Konvergenz des Integrals sind.
   Wenn das Integral nicht in geschlossener Form berechnet werden kann, gibt diese Funktion ein nicht berechnetes LaplaceTransform- Objekt zurück.
   Wenn Sie die Option noconds = True setzen , gibt die Funktion nur F (s) zurück .
2. Inverse Laplace-Transformationsfunktion:
   
   sympy.integrals.transforms. inverse_laplace_transform (F, s, t, plane = None, ** Hinweise).
   
   Die Funktion inverse_laplace_transform () führt die inverse Laplace-Transformation der Funktion der komplexen Variablen F (s) in die Funktion f (t) der realen Variablen durch, so dass:
   

   $$

   $$f (t) = \ frac {1} {2 \ pi i} \ int_ {c-∞ \ cdot i} ^ {c + ∞ \ cdot i} e ^ {st} F (s) ds.$$
   
   Wenn das Integral nicht in geschlossener Form berechnet werden kann, gibt diese Funktion die nicht aufgerufene InverseLaplaceTransform des Objekts zurück.
   

Die inverse Laplace-Transformation am Beispiel der Bestimmung der Übergangseigenschaften von Reglern

Die Übertragungsfunktion des PID-Reglers hat die Form [2]:

$$

$$W (s) = (1+ \ frac {K_ {d} \ cdot T_ {d} \ cdot s} {1 + T_ {d} \ cdot s}) \ cdot K_ {p} \ cdot (1+ \ frac {1} {T_ {i} \ cdot s}) \ cdot \ frac {1} {s}.$$

Wir werden ein Programm schreiben, um Gleichungen für die Übergangseigenschaften der PID- und PI-Regler für die reduzierte Übertragungsfunktion zu erhalten und zusätzlich die Zeit abzuleiten, die für die inverse visuelle Laplace-Transformation aufgewendet wird.


Wir bekommen:

Reverse Visual Laplace-Transformationszeit: 2,68 s



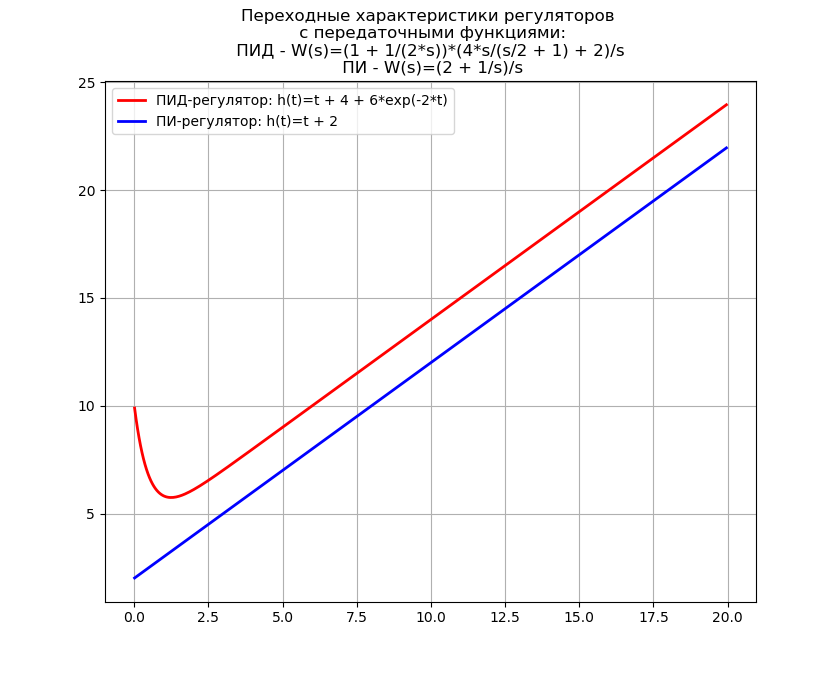
Die inverse Laplace-Transformation wird häufig bei der Synthese von selbstfahrenden Kanonen verwendet, bei denen Python teure Software-Monster wie MathCAD ersetzen kann. Daher ist die obige Verwendung der inversen Transformation von praktischer Bedeutung.

Laplace-Transformation aus Derivaten höherer Ordnung zur Lösung des Cauchy-Problems

Unsere Diskussion wird mit der Anwendung von Laplace-Transformationen (Laplace-Bildern) auf die Suche nach Lösungen einer linearen Differentialgleichung mit konstanten Koeffizienten der Form fortgesetzt:

$$

$$a \ cdot x '' (t) + b \ cdot x '(t) + c \ cdot x (t) = f (t). (1)$$

Wenn a und b Konstanten sind, dann

$$

$$L \ left \ {a \ cdot f (t) + b \ cdot q (t) \ right \} = a \ cdot L \ left \ {f (t) \ right \} + b \ cdot L \ left \ {q (t) \ right \} (2)$$

für alle s, so dass beide Laplace-Transformationen (Laplace-Bild) der Funktionen f (t) und q (t) existieren.

Lassen Sie uns die Linearität der direkten und inversen Laplace-Transformationen mit den zuvor betrachteten Funktionen laplace_transform () und inverse_laplace_transform () überprüfen . Dazu nehmen wir als Beispiel f (t) = sin (3t) , q (t) = cos (7t) , a = 5 , b = 7 und verwenden das folgende Programm.


Wir bekommen:

(7 * s ** 3 + 15 * s ** 2 + 63 * s + 735) / ((s ** 2 + 9) * (s ** 2 + 49))
(7 * s ** 3 + 15 * s ** 2 + 63 * s + 735) / ((s ** 2 + 9) * (s ** 2 + 49))
Stimmt
5 * sin (3 * t) + 7 * cos (7 * t)
5 * sin (3 * t) + 7 * cos (7 * t)

Der obige Code zeigt auch die Einzigartigkeit der inversen Laplace-Transformation.

Vorausgesetzt, das $$$q (t) = f '(t)$ erfüllt die Bedingungen des ersten Satzes, dann folgt aus diesem Satz:

$$

$$L \ left \ {f '' (t) \ right \} = L \ left \ {q '(t) \ right \} = sL \ left \ {q (t) \ right \} - q (0) = sL \ left \ {f '(t) \ right \} - f' (0) = s \ left [sL \ left \ {f (t) -f (0) \ right \} \ right],$$

und damit

$$

$$L \ left \ {f '' (t) \ right \} = s ^ {2} \ cdot F (s) -s \ cdot f (0) -f '(0).$$

Das Wiederholen dieser Berechnung ergibt

$$

$$L \ left \ {f '' '(t) \ right \} = sL \ left \ {f' '(t) \ right \} - f' '(0) = s ^ {3} F (s) -s ^ {2} f (0) -sf '(0) -f' '(0).$$

Nach einer endlichen Anzahl solcher Schritte erhalten wir die folgende Verallgemeinerung des ersten Satzes:

$$

$$L \ left \ {f ^ {(n)} (t) \ right \} = s ^ {n} L \ left \ {f (t) \ right \} - s ^ {n-1} f (0 ) -s ^ {n-2} f '(0) - \ cdot \ cdot \ cdot -f ^ {(n-1)} (0) =$$

$$

$$= s ^ {n} F (s) -s ^ {n-1} f (0) - \ cdot \ cdot \ cdot -sf ^ {(n-2)} (0) -f ^ {(n- 1)} (0). (3)$$

Wenn wir die Beziehung (3), die die Laplace-transformierten Derivate der gewünschten Funktion mit Anfangsbedingungen enthält, auf Gleichung (1) anwenden , können wir ihre Lösung gemäß der in unserer Abteilung speziell entwickelten Methode mit aktiver Unterstützung von Scorobey für die SymPy-Bibliothek erhalten.

Eine Methode zum Lösen linearer Differentialgleichungen und Gleichungssysteme basierend auf Laplace-Transformationen unter Verwendung der SymPy-Bibliothek

Um die Methode zu demonstrieren, verwenden wir eine einfache Differentialgleichung, die die Bewegung eines Systems beschreibt, das aus einem Materialpunkt einer bestimmten Masse besteht, der auf einer Feder montiert ist, auf die eine externe Kraft ausgeübt wird. Die Differentialgleichung und die Anfangsbedingungen für ein solches System haben die Form:

$$

$$x '' + 4x = \ sin (3t); x (0) = 1,2; x '(0) = 1, (4)$$

wo $$$x (0)$ - reduzierte Ausgangsposition der Masse, $$$x '(0)$ - reduzierte anfängliche Massengeschwindigkeit.

Ein vereinfachtes physikalisches Modell, definiert durch Gleichung (4) mit Anfangsbedingungen ungleich Null [1]:



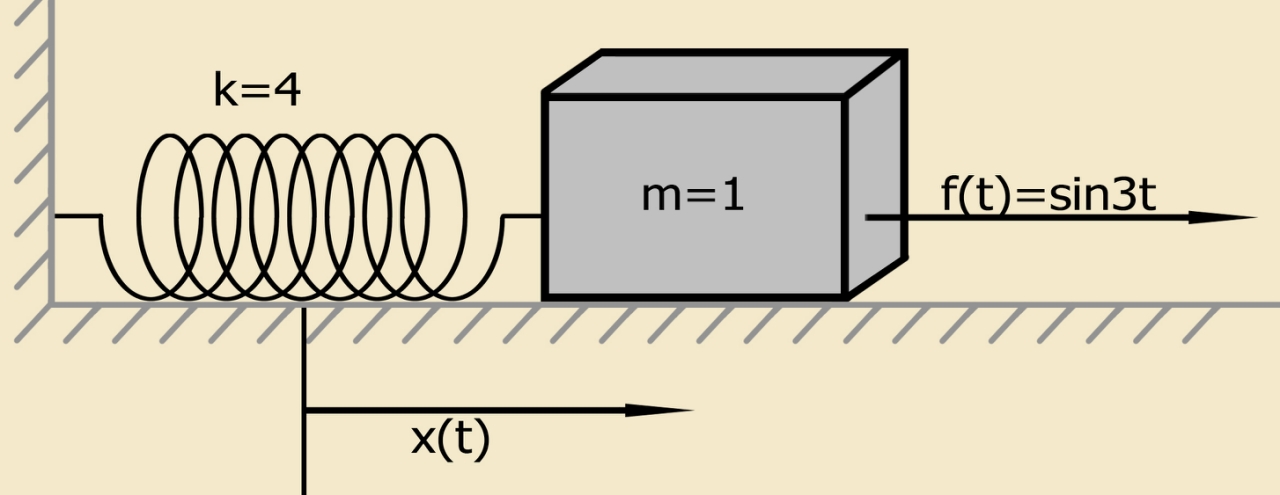
Ein System, das aus einem Materialpunkt einer bestimmten Masse besteht, der an einer Feder befestigt ist, erfüllt das Cauchy-Problem (ein Problem mit Anfangsbedingungen). Der Materialpunkt einer gegebenen Masse befindet sich zunächst in ihrer Gleichgewichtsposition.

Um diese und andere lineare Differentialgleichungen mit der Laplace-Transformationsmethode zu lösen, ist es zweckmäßig, das folgende System zu verwenden, das aus den Beziehungen (3) erhalten wird:
$$$L \ left \ {f ^ {IV} (t) \ right \} = s ^ {4} \ cdot F (s) -s ^ {3} \ cdot f (0) -s ^ {2} \ cdot f ^ {I} (0) -s \ cdot f ^ {II} (0) -f ^ {III} (0),$
$$$L \ left \ {f ^ {III} (t) \ right \} = s ^ {3} \ cdot f (s) -s ^ {2} \ cdot f (0) -s \ cdot f ^ {I. } (0) -f ^ {II} (0),$
$$$L \ left \ {f ^ {II} (t) \ right \} = s ^ {2} \ cdot F (s) -s \ cdot f (0) -f ^ {I} (0),$
$$$L \ left \ {f ^ {I} (t) \ right \} = s \ cdot F (s) -f (0), L \ left \ {f (t) \ right \} = F (s) .$
$$$L \ left \ {f (t) \ right \} = F (s). (5)$

Die Reihenfolge der Lösungen mit SymPy ist wie folgt:

1. Laden Sie die erforderlichen Module und definieren Sie explizit symbolische Variablen:
   
   

    from sympy import * import numpy as np import matplotlib.pyplot as plt var('s') var('t', positive=True) var('X', cls=Function) 

   
   
2. Geben Sie die Version der Sympy-Bibliothek an, um deren Funktionen zu berücksichtigen. Geben Sie dazu folgende Zeilen ein:
   
   

    import SymPy print ('  sympy – %' % (sympy._version_)) 

   
   
3. Entsprechend der physikalischen Bedeutung des Problems wird die Zeitvariable für eine Region bestimmt, die Null und positive Zahlen enthält. Wir setzen die Anfangsbedingungen und die Funktion auf der rechten Seite von Gleichung (4) mit ihrer nachfolgenden Laplace-Transformation. Für Anfangsbedingungen müssen Sie die Rational-Funktion verwenden, da die Verwendung der Dezimalrundung zu einem Fehler führt.
   
   

    #    : x0 = Rational(6, 5) #   : x01 = Rational(1, 1) g = sin(3*t) Lg = laplace_transform(g, t, s, noconds=True) 

   
   
4. Mit (5) schreiben wir die Laplace-konvertierten Ableitungen auf der linken Seite von Gleichung (4) neu, bilden daraus die linke Seite dieser Gleichung und vergleichen das Ergebnis mit der rechten Seite:
   
   

    d2 = s**2*X(s) - s*x0 - x01 d0 = X(s) d = d2 + 4*d0 de = Eq(d, Lg) 

   
   
5. Wir lösen die erhaltene algebraische Gleichung für die Transformation X (s) und führen die inverse Laplace-Transformation durch:
   
   

    rez = solve(de, X(s))[0] soln = inverse_laplace_transform(rez, s, t) 

   
   
6. Wir übertragen von der Arbeit in der SymPy-Bibliothek in die NumPy-Bibliothek:
   
   

    f = lambdify(t, soln, 'numpy') 

   
   
7. Wir zeichnen die übliche Python-Methode:
   
   

    x = np.linspace(0, 6*np.pi, 100) plt.title(',     \n  :\n  (t)=%s' % soln) plt.grid(True) plt.xlabel('t', fontsize=12) plt.ylabel('x(t)', fontsize=12) plt.plot(x, f(x), 'g', linewidth=2) plt.show() 

   
   

Wir bekommen:
Sympy-Bibliotheksversion - 1.3



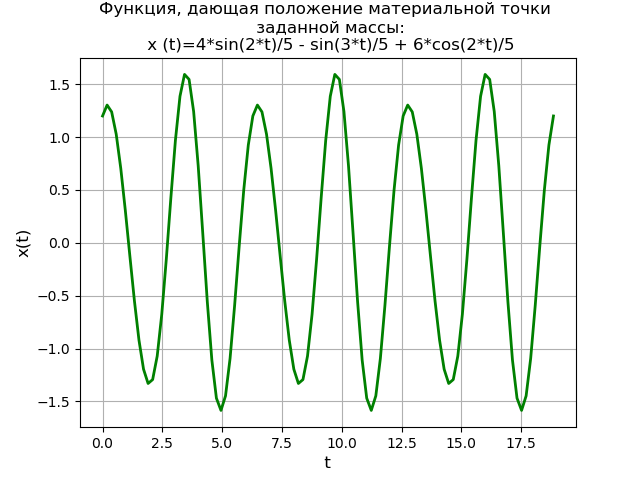
Man erhält ein Diagramm der periodischen Funktion, das die Position des Materialpunktes einer gegebenen Masse angibt. Die Laplace-Transformationsmethode unter Verwendung der SymPy-Bibliothek bietet eine Lösung nicht nur ohne die Notwendigkeit, zuerst eine allgemeine Lösung für eine homogene Gleichung und eine bestimmte Lösung für die anfängliche heterogene Differentialgleichung zu finden, sondern auch ohne die Notwendigkeit, die Elementarfraktionsmethode und Laplace-Tabellen zu verwenden.

Gleichzeitig bleibt der pädagogische Wert der Lösungsmethode erhalten, da das System (5) verwendet werden muss, und gehen Sie zu NumPy, um Lösungen mit produktiveren Methoden zu untersuchen.

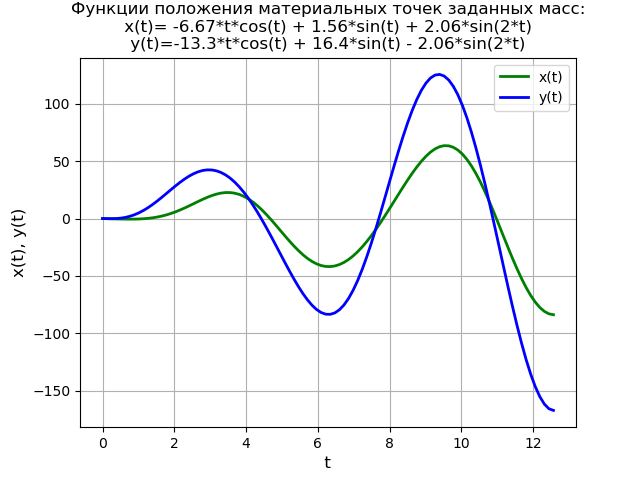
Um die Methode weiter zu demonstrieren, lösen wir das Differentialgleichungssystem:
$$$\ begin {Fälle} 2x '' + 6x-2 = 0, \\ y '' - 2x + 2y = 40 \ cdot \ sin (3t), \ end {Fälle} (6)$
mit Anfangsbedingungen $$$x (0) = y (0) = y '(0) = 0.$

Ein vereinfachtes physikalisches Modell, das durch das Gleichungssystem (6) unter Null-Anfangsbedingungen definiert wird:



Somit wird die Kraft f (t) zum Zeitpunkt t = 0 plötzlich auf den zweiten Materialpunkt einer gegebenen Masse ausgeübt , wenn das System in seiner Gleichgewichtsposition ruht.

Die Lösung des Gleichungssystems ist identisch mit der zuvor betrachteten Lösung der Differentialgleichung (4), daher gebe ich den Text des Programms ohne Erklärung an.


Wir bekommen: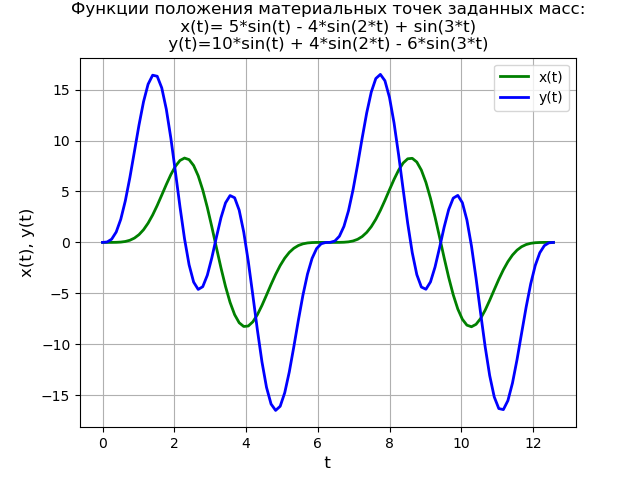



Bei Anfangsbedingungen ungleich Null hat der Programmtext und das Funktionsdiagramm die Form:




Betrachten Sie die Lösung einer linearen Differentialgleichung vierter Ordnung mit Anfangsbedingungen von Null:
$$$x ^ {(4)} + 2 \ cdot x '' + x = 4 \ cdot t \ cdot e ^ {t};$
$$$x (0) = x '(0) = x' '(0) = x ^ {(3)} (0) = 0.$


Entscheidungsplan:



Wir lösen die lineare Differentialgleichung vierter Ordnung:
$$$x ^ {(4)} + 13x '' + 36x = 0;$
mit Anfangsbedingungen $$$x (0) = x '' (0) = 0$ , $$$x '(0) = 2$ , $$$x ^ {(3)} (0) = - 13$ .


Entscheidungsplan: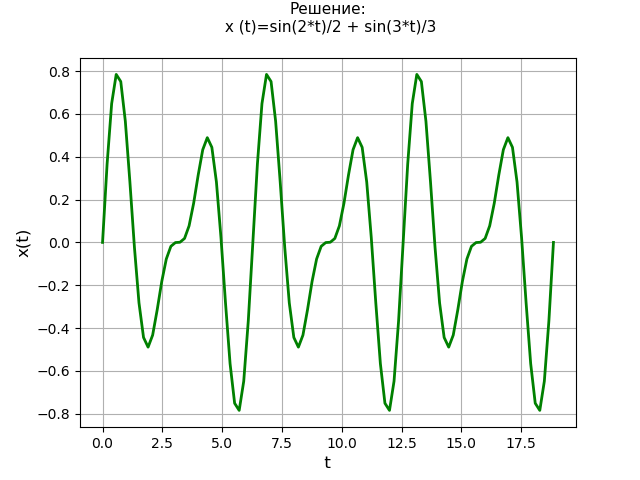

Funktionen zum Lösen von ODE

Für ODE- und ODE-Systeme mit einer analytischen Lösung wird die Funktion dsolve () verwendet:
sympy.solvers.ode. dsolve (Gl., func = Keine, Hinweis = 'Standard', Vereinfachen = Wahr, ics = Keine, xi = Keine, eta = Keine, x0 = 0, n = 6, ** kwargs)

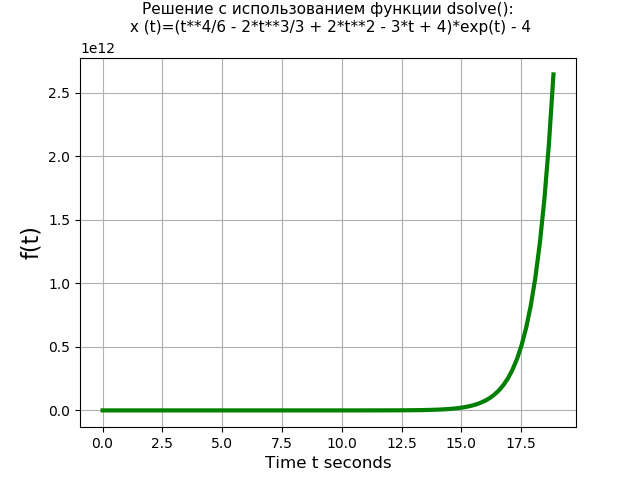
Vergleichen wir die Leistung der Funktion dsolve () mit der Laplace-Methode. Nehmen Sie zum Beispiel die folgende Differentialgleichung vierten Grades mit Null-Anfangsbedingungen:
$$$x ^ {(IV)} (t) = 3 \ cdot x '' '(t) -x (t) = 4 \ cdot t \ cdot \ exp (t);$
$$$x (0) = x '(0) = x' '(0) = x' '' (0) = 0.$


Wir bekommen:

Gleichungszeit mit der Funktion dsolve (): 1.437 s




Wir bekommen:

Gleichungszeit mit der Laplace-Transformation: 3,274 s



Die Funktion dsolve () (1,437 s) löst die Gleichung vierter Ordnung also schneller als die Lösung mit der Laplace-Transformationsmethode (3,274 s) mehr als zweimal. Es ist jedoch zu beachten, dass die Funktion dsolve () das System der Differentialgleichungen zweiter Ordnung nicht löst. Wenn beispielsweise das System (6) mit der Funktion dsolve () gelöst wird, tritt ein Fehler auf:

 from sympy import* t = symbols('t') x, y = symbols('x, y', Function=True) eq = (Eq(Derivative(x(t), t, 2), -3*x(t) + y(t)), Eq(Derivative(y(t), t, 2), 2*x(t) - 2*y(t) + 40*sin(3*t))) rez = dsolve(eq) print (list(rez)) 

Wir bekommen:

raiseNotImplementedError
NotImplementedError

Dieser Fehler bedeutet, dass die Lösung des Differentialgleichungssystems mit der Funktion dsolve () nicht symbolisch dargestellt werden kann. Während wir mit Hilfe von Laplace-Transformationen eine symbolische Darstellung der Lösung erhalten haben, beweist dies die Wirksamkeit der vorgeschlagenen Methode.

Hinweis

Um die erforderliche Methode zum Lösen von Differentialgleichungen mit der Funktion dsolve () zu finden , müssen Sie classify_ode (eq, f (x)) verwenden , zum Beispiel:

 from sympy import * from IPython.display import * import matplotlib.pyplot as plt init_printing(use_latex=True) x = Symbol('x') f = Function('f') eq = Eq(f(x).diff(x, x) + f(x), 0) print (dsolve(eq, f(x))) print (classify_ode(eq, f(x))) eq = sin(x)*cos(f(x)) + cos(x)*sin(f(x))*f(x).diff(x) print (classify_ode(eq, f(x))) rez = dsolve(eq, hint='almost_linear_Integral') print (rez) 

Wir bekommen:

Gleichung (f (x), C1 · sin (x) + C2 · cos (x))
('nth_linear_constant_coeff_homogene', '2nd_power_series_ordinary')
('trennbar', '1st_exact', 'fast_linear', '1st_power_series', 'lie_group', 'separable_Integral', '1st_exact_Integral', 'fast_linear_Integral')
[Gleichung (f (x), -acos ((C1 + Integral (0, x)) * exp (-Integral (-tan (x), x))) + 2 * pi), Gleichung (f (x), acos ((C1 + Integral (0, x)) * exp (-Integral (-tan (x), x))]]

Für die Gleichung eq = Gl (f (x) .diff (x, x) + f (x), 0) funktioniert also jede Methode aus der ersten Liste:

nth_linear_constant_coeff_homogene,
2nd_power_series_ordinary

Für die Gleichung eq = sin (x) * cos (f (x)) + cos (x) * sin (f (x)) * f (x) .diff (x) funktioniert jede Methode aus der zweiten Liste:

trennbar, 1st_exact, fast_linear,
1st_power_series, lie_group, separable_Integral,
1st_exact_Integral, fast_linear_Integral

Um die ausgewählte Methode zu verwenden, hat der Funktionseintrag dsolve () die folgende Form:

 rez = dsolve(eq, hint='almost_linear_Integral') 

Fazit:

In diesem Artikel sollte gezeigt werden, wie die Tools der Bibliotheken SciPy und NumPy am Beispiel der Lösung linearer ODE-Systeme mithilfe der Operatormethode verwendet werden. Daher wurden die Methoden zur symbolischen Lösung linearer Differentialgleichungen und Gleichungssysteme nach der Laplace-Methode berücksichtigt. Die Leistungsanalyse dieser Methode und der in der Funktion dsolve () implementierten Methoden wird durchgeführt.

Referenzen:

1. Differentialgleichungen und Randwertprobleme: Modellierung und Berechnung mit Mathematica, Maple und MATLAB. 3. Auflage .: Per. aus dem Englischen - M.: LLC “I.D. Williams, 2008. - 1104 p.: Ill. - Paral. tit. Englisch
2. Verwenden der inversen Laplace-Transformation zur Analyse der dynamischen Verbindungen von Steuerungssystemen