Lerne OpenGL. Lektion 6.1. PBR oder physikalisch korrektes Rendern. Theorie

Physikalisch korrektes Rendern

PBR oder physikalisch basiertes Rendering ist eine Reihe von Visualisierungstechniken, die auf einer Theorie basieren, die recht gut mit der realen Theorie der Lichtausbreitung übereinstimmt. Da der Zweck von PBR eine physikalisch zuverlässige Lichtsimulation ist, sieht es im Vergleich zu den zuvor verwendeten Beleuchtungsmodellen Phong und Blinn-Fong viel realistischer aus. Es sieht nicht nur besser aus, sondern bietet auch eine gute Annäherung an die reale Physik, die es uns (und insbesondere Künstlern) ermöglicht, Materialien basierend auf den physikalischen Eigenschaften von Oberflächen zu erstellen, ohne auf billige Tricks zurückgreifen zu müssen, um die Beleuchtung realistisch erscheinen zu lassen. Der Hauptvorteil dieses Ansatzes besteht darin, dass die von uns erstellten Materialien unabhängig von den Lichtverhältnissen wie geplant aussehen, was nicht über andere, nicht über PBR-Ansätze gesagt werden kann.

PBR ist jedoch immer noch eine Annäherung an die Realität (basierend auf den Gesetzen der Physik), weshalb es eher als physikalisch korrektes Rendering als als physikalisches Rendering bezeichnet wird. Damit das Beleuchtungsmodell als physikalisch korrekt bezeichnet werden kann, muss es drei Bedingungen erfüllen (keine Sorge, wir werden sie bald erreichen):

• Basierend auf einem Modell reflektierender Mikrofacetten
• Befolgen Sie das Gesetz der Energieerhaltung
• Verwenden Sie die Doppelstrahl-Reflexionsverteilungsfunktion (BRDF).

In dieser Tutorial-Reihe konzentrieren wir uns auf den PBR-Ansatz, der ursprünglich bei Disney entwickelt und für die Echtzeitvisualisierung durch Epic Games angepasst wurde. Ihr Ansatz, der auf einem metalldielektrischen Arbeitsablauf basiert (engl. Metallischer Arbeitsablauf, konnte keine bessere Übersetzung finden - ca. Hrsg. ), Ist gut dokumentiert, in vielen gängigen Motoren weit verbreitet und sieht erstaunlich aus. Am Ende dieses Abschnitts erhalten wir etwas Ähnliches:

Beachten Sie, dass die Artikel in diesem Abschnitt ziemlich fortgeschritten sind. Es wird daher empfohlen, dass Sie sich mit OpenGL und Shader-Beleuchtung gut auskennen. Hier sind einige der Kenntnisse, die Sie benötigen, um diesen Abschnitt zu studieren: Bildpuffer , kubische Karten , Gammakorrektur , HDR und normale Karten . Wir werden auch etwas tiefer in die Mathematik gehen, aber ich verspreche, alles zu tun, um alles so klar wie möglich zu erklären.

Modell reflektierender Mikrofacetten

Alle PBR-Techniken basieren auf der Theorie der Mikrogesichter. Diese Theorie besagt, dass jede Oberfläche mit hoher Vergrößerung als ein Satz mikroskopischer Spiegel dargestellt werden kann, die als Mikroflächen bezeichnet werden. Aufgrund der Oberflächenrauheit können diese Mikrospiegel in verschiedene Richtungen ausgerichtet werden:

Je rauer die Oberfläche ist, desto zufälliger sind die Mikroflächen ausgerichtet. Das Ergebnis dieser Anordnung dieser kleinen Spiegel ist (insbesondere bei Spiegelreflexionen und Reflexionen), dass die einfallenden Lichtstrahlen auf rauen Oberflächen in verschiedene Richtungen gestreut werden, was zu einer breiteren Spiegelreflexion führt. Und umgekehrt: Auf glatten Oberflächen werden die einfallenden Strahlen eher in eine Richtung reflektiert, was zu einer kleineren und schärferen Blendung führt:

Auf mikroskopischer Ebene gibt es keine absolut glatten Oberflächen. Angesichts der Tatsache, dass die Mikroflächen klein genug sind und wir sie innerhalb unseres Pixelraums nicht unterscheiden können, approximieren wir die Oberflächenrauheit statistisch, indem wir einen Rauheitskoeffizienten einführen. Mit diesem Koeffizienten können wir den Anteil der Mikroflächen berechnen, die in Richtung eines bestimmten Vektors ausgerichtet sind $$$h$ . Dieser Vektor $$$h$ nichts weiter als ein Medianvektor, der in der Mitte zwischen der Richtung des einfallenden Lichts liegt $$$l$ und Richtung des Beobachters $$$v$ . Wir haben bereits in einer Lektion über fortgeschrittene Beleuchtung darüber gesprochen , in der wir das Verhältnis der Summe der Vektoren definiert haben $$$l$ und $$$v$ auf die Länge des resultierenden Vektors:

$$

$$h = \ frac {l + v} {|| l + v ||}$$

Je mehr Mikroflächen in Richtung des Medianvektors ausgerichtet sind, desto schärfer und heller wird das Glanzlicht. Aufgrund des Rauheitskoeffizienten, der zwischen 0 und 1 liegt, können wir die Ausrichtung der Mikroflächen statistisch approximieren:

Wie Sie sehen können, ergibt ein höherer Wert des Rauheitskoeffizienten einen größeren Spiegelfleckfleck als ein kleiner und scharfer Fleck auf glatten Oberflächen.

Energieeinsparung.

Die Verwendung der Näherung unter Berücksichtigung von Mikroflächen bringt bereits eine bestimmte Form der Energieeinsparung mit sich: Die Energie des reflektierten Lichts wird niemals die Energie des einfallenden Lichts überschreiten (wenn die Oberfläche nicht von selbst leuchtet). Wenn wir das obige Bild betrachten, sehen wir, dass mit zunehmender Oberflächenrauheit der Punkt des reflektierten Lichts zunimmt, gleichzeitig aber seine Helligkeit abnimmt. Wenn die Intensität des reflektierten Lichts unabhängig von der Größe des Spots für alle Pixel gleich wäre, würden rauere Oberflächen viel mehr Energie emittieren, was gegen das Gesetz der Energieerhaltung verstoßen würde. Daher sind Spiegelreflexionen auf glatten Oberflächen heller und auf rauen Oberflächen dunkler.

Um Energie zu sparen, müssen wir eine klare Trennung zwischen der diffusen und der Spiegelkomponente vornehmen. In diesem Moment, wenn ein Lichtstrahl die Oberfläche erreicht, wird er in reflektierte und gebrochene Komponenten unterteilt. Die reflektierte Komponente ist direkt reflektiertes Licht und dringt nicht in die Oberfläche ein. Wir kennen sie als Spiegelkomponente des Lichts. Die gebrochene Komponente ist Licht, das die Oberfläche durchdringt und von dieser absorbiert wird - es ist uns als diffuse Komponente des Lichts bekannt.

Mit der Absorption von Licht sind jedoch einige Nuancen verbunden - dies geschieht nicht sofort, sobald das Licht die Oberfläche berührt. Aus der Physik wissen wir, dass Licht als ein Photonenstrahl mit Energie beschrieben werden kann, der sich in einer geraden Linie bewegt, bis er infolge einer Kollision mit Hindernissen die gesamte Energie verliert. Jedes Material besteht aus Mikropartikeln, die mit einem Lichtstrahl interagieren können, wie in der folgenden Abbildung gezeigt. Diese Partikel absorbieren bei jeder Kollision einen Teil oder die gesamte Energie des Lichts und wandeln es in Wärme um.

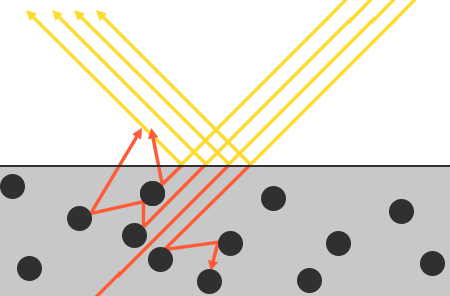
Im allgemeinen Fall wird nicht die gesamte Energie absorbiert, und das Licht streut weiterhin in (überwiegend) zufälligen Richtungen, wo es erneut mit anderen Partikeln kollidiert, bis ihm die Energie ausgeht oder die Oberfläche wieder verlässt. Somit beginnt die Oberfläche, Lichtstrahlen wieder zu emittieren, was einen Beitrag in Form der beobachteten (diffusen) Farbe der Oberfläche leistet. Mit PBR gehen wir vereinfacht davon aus, dass das gesamte gebrochene Licht über einen kleinen Einflussbereich absorbiert und gestreut wird, wobei der Effekt des gestreuten Lichts, das die Oberfläche in einem Abstand von diesem Bereich verlässt, ignoriert wird. Spezielle Shadertechniken, die dies berücksichtigen, sogenannte Streutechniken unter der Oberfläche , verbessern die visuelle Qualität von Materialien wie Leder, Marmor, Wachs erheblich, sind jedoch hinsichtlich der Leistung teuer.

Zusätzliche Feinheiten treten auf, wenn Licht auf Metalloberflächen gebrochen und reflektiert wird. Metalloberflächen interagieren anders mit Licht als nichtmetallische (d. H. Dielektrika). Sie gehorchen denselben Gesetzen der Brechung und Reflexion, mit einer Ausnahme: Alles gebrochene Licht wird von der Oberfläche absorbiert, ohne zu streuen, nur spiegelreflektiertes Licht bleibt übrig; Mit anderen Worten, Metalloberflächen haben keine diffuse Farbe. Aufgrund dieses offensichtlichen Unterschieds zwischen Metallen und Dielektrika werden sie im PBR-Förderer, in den wir im Verlauf dieses Artikels weiter gehen, unterschiedlich verarbeitet.

Dieser Unterschied zwischen reflektiertem und gebrochenem Licht führt uns zu einer weiteren Beobachtung hinsichtlich der Energieeinsparung: Ihre Werte schließen sich gegenseitig aus. Die Energie des reflektierten Lichts kann vom Material nicht absorbiert werden. Daher ist die von der Oberfläche in Form von gebrochenem Licht absorbierte Energie die verbleibende Energie nach Berücksichtigung des reflektierten Lichts.
Wir verwenden dieses Verhältnis, indem wir zuerst den reflektierten Teil als Prozentsatz der Energie der einfallenden Strahlen berechnen, die von der Oberfläche reflektiert werden, und dann den Anteil des gebrochenen Lichts direkt von der reflektierten, als:

float kS = calculateSpecularComponent(...); // /  float kD = 1.0 - kS; // /  

Auf diese Weise lernen wir dank des Gesetzes der Energieerhaltung die Bedeutung sowohl der reflektierten als auch der gebrochenen Teile. Bei diesem Ansatz wird weder der gebrochene (diffuse) noch der reflektierte Teil 1,0 überschreiten, wodurch sichergestellt wird, dass ihre Gesamtenergie den Wert der einfallenden Lichtenergie nicht überschreitet, den wir in früheren Lektionen nicht berücksichtigen konnten.

Reflexionsgleichung

Das Obige führt uns zu der sogenannten Rendering-Gleichung : Eine komplexe Gleichung, die von sehr klugen Leuten erfunden wurde und heute das beste Modell für die Simulation von Beleuchtung ist. PBR folgt streng einer spezifischeren Version dieser Gleichung, die als Reflexionsgleichung bekannt ist . Um PBR gut zu verstehen, ist es wichtig, zunächst die Reflexionsgleichung vollständig zu verstehen:

$$

$$L_o (p, \ omega_o) = \ int \ limit_ \ Omega f_r (p, \ omega_i, \ omega_o) L_i (p, \ omega_i) n \ cdot \ omega_id \ omega_i$$

Zuerst sieht es beängstigend aus, aber wir werden es nach und nach teilweise auseinander nehmen, und Sie werden sehen, wie langsam es Sinn macht. Um diese Gleichung zu verstehen, müssen wir etwas tiefer in die Radiometrie gehen. Radiometrie ist die Wissenschaft der Messung elektromagnetischer Strahlung (einschließlich sichtbarem Licht). Es gibt mehrere radiometrische Größen, mit denen wir die Beleuchtung messen können, aber wir werden nur eine verwenden, die sich auf die Reflexionsgleichung bezieht, die als Energieluminanz (englische Strahlung) bekannt ist und hier mit dem Buchstaben L bezeichnet wird. EI wird verwendet, um die Größe oder Intensität des Lichts zu quantifizieren. aus einer bestimmten Richtung kommen. EJ wiederum ist eine Kombination mehrerer physikalischer Größen, und damit wir uns das leichter vorstellen können, werden wir uns auf jede einzelne konzentrieren.

Strahlungsfluss

Strahlungsfluss ( $$$\ Phi$ ) ist die Leistung der durch Licht übertragenen Energie, gemessen in Watt. Die Gesamtenergie des Lichts besteht aus vielen Begriffen für verschiedene Wellenlängen, von denen jeder seiner eigenen Farbe des Spektrums entspricht. Die von der Lichtquelle emittierte Energie kann in diesem Fall als Funktion aller dieser Wellenlängen dargestellt werden. Wellenlängen von 390 nm bis 700 nm bilden den sichtbaren Teil des Spektrums, dh Strahlung in diesem Bereich kann vom menschlichen Auge wahrgenommen werden. Im Bild unten sehen Sie die Werte der Energien für verschiedene Wellenlängen, aus denen das Tageslicht besteht:

Der Strahlungsfluss entspricht für alle Wellenlängen der Fläche unter dem Diagramm dieser Funktion. Die direkte Verwendung von Lichtwellenlängen als Eingabe in Computergrafiken ist unpraktisch, daher greifen wir auf eine vereinfachte Darstellung des Strahlungsflusses zurück, anstatt eine Funktion aller Wellenlängen, ein Triplett von Farben, bekannt als RGB (oder, wie wir es normalerweise nennen, die Farbe der Beleuchtung) zu verwenden. Eine solche Ansicht führt zu einem gewissen Informationsverlust, wirkt sich jedoch insgesamt geringfügig auf das endgültige Bild aus.

Raumwinkel

Raumwinkel bezeichnet mit $$$\ omega$ gibt uns die Größe oder Fläche der Figur, die auf die Einheitskugel projiziert wird. Sie können es sich als eine Richtung vorstellen, die ein Volumen von:

Stellen Sie sich vor, Sie befinden sich in der Mitte einer Kugel und schauen in Richtung der Figur. Die Größe der resultierenden Silhouette ist ein Raumwinkel.

Strahlungsintensität

Die Strahlungsstärke misst die Menge des Strahlungsflusses pro Raumwinkel oder die Stärke einer Lichtquelle pro Flächeneinheit, die durch den Raumwinkel definiert wird. Beispielsweise bedeutet für eine omnidirektionale Lichtquelle, die gleichmäßig in alle Richtungen emittiert, die Strahlungskraft die Energie des Lichts pro bestimmten Bereich (Raumwinkel):

Die Gleichung, die die Stärke der Strahlung beschreibt, sieht folgendermaßen aus:

$$

$$I = \ frac {d \ Phi} {d \ omega}$$

, wobei I der Strahlungsfluss f pro Raumwinkel ist $$${d \ omega}$

Wenn wir den Strahlungsfluss, die Kraft und den Raumwinkel kennen, können wir die Energiehelligkeitsgleichung beschreiben, die die gesamte beobachtete Energie im Bereich A beschreibt, begrenzt durch den Raumwinkel O für Licht durch Kraft $$$\ Phi$

$$

$$L = \ frac {d ^ 2 \ Phi} {dA d \ omega \ cos \ theta}$$

Die Energiehelligkeit ist die radiometrische Lichtmenge in einem Bereich, die vom Einfallswinkel abhängt. $$$\ theta$ (Winkel zwischen der Lichtrichtung und der Normalen zur Oberfläche) durch $$$cos \ theta$ : Licht ist schwächer, wenn es entlang der Oberfläche emittiert wird, und stärker, wenn es senkrecht dazu steht. Dies ähnelt unseren Berechnungen für diffuses Licht im Tutorial zu den Grundlagen der Beleuchtung seitdem $$$cos \ theta$ nichts weiter als ein Skalarprodukt zwischen der Lichtrichtung und dem Normalenvektor zur Oberfläche:

 float cosTheta = dot(lightDir, N); 

Die Energiehelligkeitsgleichung ist für uns sehr nützlich, da sie die meisten physikalischen Größen enthält, die uns interessieren. Wenn wir annehmen, dass der Raumwinkel ω und die Fläche A infinitesimal sind, können wir mit dem EE den Fluss eines Lichtstrahls pro Punkt im Raum messen. Auf diese Weise können wir den EI eines einzelnen Lichtstrahls berechnen, der auf einen einzelnen Punkt (Fragment) wirkt. Wir übersetzen tatsächlich den Raumwinkel $$$\ omega$ in Richtungsvektor $$$\ omega$ und $$$A$ auf den Punkt $$$p$ . Somit können wir den EI in unseren Shadern direkt verwenden, um den Beitrag eines einzelnen Lichtstrahls für jedes Fragment zu berechnen.

Wenn es um EE geht, interessieren wir uns normalerweise für das gesamte einfallende Licht, das auf den Punkt p fällt, der die Summe des gesamten EE darstellt und als Bestrahlungsstärke bezeichnet wird. Wenn wir den EI und die Bestrahlung kennen, können wir zur Reflexionsgleichung zurückkehren:

$$

$$L_o (p, \ omega_o) = \ int \ limit_ \ Omega f_r (p, \ omega_i, \ omega_o) L_i (p, \ omega_i) n \ cdot \ omega_id \ omega_i$$

Jetzt wissen wir das $$$L$ in der Rendering-Gleichung ist der EI für einen Punkt auf der Oberfläche p und einen unendlich kleinen Raumwinkel des einfallenden Lichts $$$\ omega_i$ , die als Eingangsrichtungsvektor betrachtet werden kann $$$\ omega_i$ . Denken Sie daran, dass Energie mit multipliziert wird $$$cos \ theta$ - der Winkel zwischen der Einfallsrichtung des Lichts und der Normalen zur Oberfläche, der in der Reflexionsgleichung des Produkts ausgedrückt wird $$$n \ cdot \ omega_i$ . Die Reflexionsgleichung berechnet die Summe der reflektierten EI $$$L_o (p, \ omega_o)$ Punkte $$$p$ in Richtung $$$ω_o$ Dies ist die ausgehende Richtung zum Beobachter. Oder sonst: $$$L_o$ misst die reflektierte Bestrahlungsstärke eines Punktes $$$p$ wenn von $$$\ omega_o$ .

Da die Reflexionsgleichung auf der Bestrahlung basiert, die die Summe aller einfallenden Strahlung ist, messen wir das Licht nicht nur aus einer einfallenden Lichtrichtung, sondern aus allen einfallenden Lichtrichtungen innerhalb der Hemisphäre $$$\ Omega$ zentriert bei $$$p$ . Es kann als eine halbe Kugel beschrieben werden, die entlang der Oberflächennormalen ausgerichtet ist $$$n$ ::

Um die Summe aller Werte innerhalb der Region oder im Fall einer Halbkugel das Volumen zu berechnen, integrieren wir die Gleichung in alle eingehenden Richtungen $$$d \ omega_i$ innerhalb der Hemisphäre $$$\ Omega$ . Da es sowohl für die Rendergleichung als auch für die Reflexionsgleichung keine analytische Lösung gibt, werden wir das Integral numerisch lösen. Dies bedeutet, dass wir Ergebnisse für kleine diskrete Schritte der Halbkugelreflexionsgleichung erhalten $$$\ Omega$ und mittle sie über die Größe der Stufe. Dies nennt man die Riemannsche Summe , die wir grob mit folgendem Code darstellen können:

 int steps = 100; float sum = 0.0f; vec3 P = ...; vec3 Wo = ...; vec3 N = ...; float dW = 1.0f / steps; for(int i = 0; i < steps; ++i) { vec3 Wi = getNextIncomingLightDir(i); sum += Fr(P, Wi, Wo) * L(P, Wi) * dot(N, Wi) * dW; } 

dW für jeden einzelnen Schritt kann als betrachtet werden $$$d \ omega_i$ in der Reflexionsgleichung. Mathematisch $$$d \ omega_i$ ist das Differential, mit dem wir das Integral berechnen, und obwohl es nicht dasselbe wie dW im Code ist (da dies ein diskreter Schritt der Riemann-Summe ist), können wir es zur Vereinfachung der Berechnung als solches betrachten. Denken Sie daran, dass die Verwendung diskreter Schritte immer einen ungefähren Betrag ergibt, nicht den genauen Wert des Integrals. Ein aufmerksamer Leser wird feststellen, dass wir die Genauigkeit der Riemannschen Summe erhöhen können, indem wir die Anzahl der Schritte erhöhen.

Die Reflexionsgleichung summiert die Strahlung aller einfallenden Lichtrichtungen $$$\ omega_i$ Hemisphäre $$$\ Omega$ das erreicht den Punkt $$$p$ und gibt die Menge des reflektierten Lichts zurück $$$L_o$ in Richtung des Betrachters. Die einfallende Strahlung kann von Lichtquellen stammen, mit denen wir bereits vertraut sind, oder von Umgebungskarten, die den EI jeder einfallenden Richtung bestimmen, über die wir im IBL-Tutorial sprechen werden.

Jetzt ist das einzige Unbekannte auf der linken Seite das Symbol $$$f_r$ , bekannt als BRDF- Funktion oder Zweistrahl -Reflexionsfunktion , die den Wert der einfallenden Strahlung basierend auf den Eigenschaften des Oberflächenmaterials skaliert (oder wiegt).

BRDF

BRDF ist eine Funktion, die die Richtung des einfallenden Lichts akzeptiert. $$$\ omega_i$ Richtung zum Betrachter $$$\ omega_o$ normal zur Oberfläche $$$n$ und Parameter $$$a$ , das ist die Oberflächenrauheit. BRDF approximiert ungefähr, wie viel jeder einzelne Lichtstrahl ist $$$\ omega_i$ trägt unter Berücksichtigung der Materialeigenschaften zum endgültigen reflektierten Licht einer opaken Oberfläche bei. Wenn die Oberfläche beispielsweise vollständig glatt ist (fast wie ein Spiegel), gibt die BRDF-Funktion für alle einfallenden Lichtstrahlen 0,0 zurück $$$\ omega_i$ mit Ausnahme eines mit dem gleichen Winkel (nach Reflexion) wie der Strahl $$$\ omega_o$ für die die Funktion 1.0 zurückgibt.

BRDF approximiert die Reflexions- und Brechungseigenschaften eines Materials basierend auf der zuvor erwähnten Theorie der Mikroflächen. Damit das BRDF physikalisch plausibel ist, muss es dem Gesetz der Energieerhaltung entsprechen, dh die Gesamtenergie des reflektierten Lichts sollte niemals die Energie des einfallenden Lichts überschreiten. Technisch gesehen wird das Blinn-Fong-Modell als BRDF angesehen, das dasselbe akzeptiert $$$\ omega_i$ und $$$\ omega_o$ am Eingang. Das Blinn-Fong-Modell wird jedoch nicht als physikalisch korrekt angesehen, da es nicht die Einhaltung des Energieerhaltungsgesetzes garantiert. Es gibt mehrere physikalisch korrekte BRDFs, um die Oberflächenreaktion auf Beleuchtung zu approximieren. Fast alle Echtzeit-Grafik-Pipelines verwenden jedoch das BRDF, das als Cook-Torrance BRDF bekannt ist .

Cook-Torrens BRDF enthält sowohl einen diffusen als auch einen Spiegelteil:

$$

$$f_r = k_df_ {lambert} + k_sf_ {cook - torrance}$$

hier $$$k_d$ - gebrochener Anteil der einfallenden Lichtenergie, $$$k_s$ - reflektiert. Die linke Seite des BRDF enthält den diffusen Teil der Gleichung, der hier als bezeichnet wird $$$f_ {lambert}$ . Dies ist die sogenannte Lambert-Streuung. Es ähnelt dem, was wir für diffuses Licht verwendet haben, und ist konstant:

$$

$$f_ {lambert} = \ frac {c} {\ pi}$$

wo $$$c$ - Albedo oder Oberflächenfarbe (diffuse Oberflächentextur). Division durch $$$\ pi$ benötigt, um das gestreute Licht zu normalisieren, da das zuvor angegebene Integral, das BRDF enthält, mit multipliziert wird $$$\ pi$ (Wir werden dies im IBL-Tutorial erfahren).

Sie werden überrascht sein, wie diese Lambertsche Streuung wie der Ausdruck für diffuses Licht aussieht, den wir zuvor verwendet haben: Die Oberflächenfarbe multipliziert mit dem Skalarprodukt zwischen der Oberflächennormalen und der Richtung des Lichts. Das Skalarprodukt ist noch vorhanden, wird aber aus BRDF abgeleitet, da wir es haben $$$n \ cdot \ omega_i$ im Integral $$$L_o$ .

Es gibt verschiedene Gleichungen für den diffusen Teil von BRDF, die realistischer aussehen, aber in Bezug auf die Leistung teurer sind. Darüber hinaus, wie die Epic Games feststellten: Lambertsche Streuung ist für die meisten Echtzeit-Rendering-Zwecke ausreichend.

Der Spiegelanteil des Cook-Torrens BRDF ist leicht verbessert und wird beschrieben als:

$$

$$f_ {cook - torrance} = \ frac {DFG} {4 (\ omega_o \ cdot n) (\ omega_i \ cdot n)}$$

Es besteht aus drei Funktionen und einem Standardisierungskoeffizienten im Nenner. Jeder der Buchstaben D, F und G repräsentiert eine bestimmte Art von Funktion, die sich einem bestimmten Teil der Reflexionseigenschaften der Oberfläche annähert. Sie sind als Normalverteilungsfunktion (NDF), Fresnel-Gleichung und Geometriefunktion bekannt:

• Normalverteilungsfunktion: Annäherung an die Anzahl der Oberflächenmikroflächen entlang des Medianvektors basierend auf der Oberflächenrauheit; Dies ist die Hauptfunktion zur Annäherung an Mikroflächen.
• Geometriefunktion: Beschreibt die Selbstschattierungseigenschaft von Mikroflächen. Wenn die Oberfläche ziemlich rau ist, können einige Mikroflächen der Oberfläche andere überlappen, wodurch die von der Oberfläche reflektierte Lichtmenge verringert wird.
• Fresnel-Gleichung: beschreibt den Oberflächenreflexionskoeffizienten unter verschiedenen Winkeln.

Jede dieser Funktionen ist eine Annäherung an ihr physikalisches Äquivalent, und für sie gibt es verschiedene Implementierungen, die auf eine genauere Annäherung an das zugrunde liegende physikalische Modell abzielen. Einige liefern realistischere Ergebnisse, andere sind in Bezug auf die Leistung effektiver. Brian Caris von Epic Games hat viel über verschiedene Arten von Approximationen geforscht, über die Sie hier mehr erfahren können. Wir werden die gleichen Funktionen wie in Unreal Engine 4 von Epic Games verwenden, nämlich: Trowbridge-Reitz GGX für D, Fresnel-Schlick- Näherung für F und Smiths Schlick-GGX für G.

Normalverteilungsfunktion

Die Normalverteilungsfunktion D approximiert statistisch die relative Oberfläche der Mikroflächen, die genau entlang des Medianvektors ausgerichtet sind $$$h$ . Es gibt viele NDFs, die die statistische Annäherung der Gesamtausrichtung von Mikroflächen unter Berücksichtigung einiger Rauheitsparameter bestimmen. Wir werden eine verwenden, die als Trowbridge-Reitz GGX bekannt ist:

$$

$$NDF_ {GGXTR} (n, h, \ alpha) = \ frac {\ alpha ^ 2} {\ pi ((n \ cdot h) ^ 2 (\ alpha ^ 2−1) +1) ^ 2}$$

hier $$$h$ Ist der Medianvektor, $$$\ alpha$ - Wert der Oberflächenrauheit. Wenn wir uns entscheiden $$$h$ Als Medianvektor zwischen der Normalen zur Oberfläche und der Richtung des Lichts und anschließender Änderung des Rauheitsparameters erhalten wir das folgende Bild:

Wenn die Rauheit klein ist (d. H. Die Oberfläche ist glatt), sind die in Richtung des Medianvektors orientierten Mikroflächen in einem kleinen Radius konzentriert. Aufgrund dieser hohen Konzentration ergibt NDF einen sehr hellen Fleck. Auf einer rauen Oberfläche, auf der Mikroflächen in zufälligeren Richtungen ausgerichtet sind, finden Sie eine viel größere Anzahl von Mikroflächen, die in Richtung des Medianvektors ausgerichtet sind $$$h$ befindet sich jedoch in einem größeren Radius, wodurch die Sonderfarbe grauer wird.

Im GLSL-Code sieht die Normalverteilungsfunktion von Trowbridge-Reitz GGX ungefähr so ​​aus:

 float DistributionGGX(vec3 N, vec3 H, float a) { float a2 = a*a; float NdotH = max(dot(N, H), 0.0); float NdotH2 = NdotH*NdotH; float nom = a2; float denom = (NdotH2 * (a2 - 1.0) + 1.0); denom = PI * denom * denom; return nom / denom; } 

Geometriefunktion

Die Geometriefunktion nähert sich statistisch der relativen Oberfläche an, wo sich ihre mikroskopischen Unregelmäßigkeiten überlappen, wodurch das Eindringen von Lichtstrahlen verhindert wird.

Wie im Fall von NDF akzeptiert die Geometriefunktion den Oberflächenrauheitskoeffizienten als Eingabe, was in diesem Fall Folgendes bedeutet: Bei raueren Oberflächen ist die Wahrscheinlichkeit einer Schattierung von Mikroflächen höher. Die Geometriefunktion, die wir verwenden werden, ist eine Kombination der GGX- und Schlick-Beckmann-Näherungen und wird als Schlick-GGX bezeichnet:

$$

$$G_ {SchlickGGX} (n, v, k) = \ frac {n \ cdot v} {(n \ cdot v) (1 - k) + k}$$

Hier $$$k$ ist eine Umbenennung $$$\ alpha$ abhängig davon, ob wir die Geometriefunktion für Direktbeleuchtung oder IBL-Beleuchtung verwenden:

$$

$$k_ {direct} = \ frac {(\ alpha + 1) ^ 2} {8}$$

$$

$$k_ {IBL} = \ frac {\ alpha ^ 2} {2}$$

Bitte beachten Sie, dass der Wert $$$\ alpha$ kann variieren, je nachdem, wie Ihr Motor die Rauheit übersetzt $$$\ alpha$ . In den folgenden Lektionen werden wir detailliert diskutieren, wie und wo diese Neuzuweisung relevant wird.

Um die Geometrie effektiv zu approximieren, müssen wir sowohl die Blickrichtung (überlappende Geometrie) als auch den Richtungsvektor des Lichts (Selbstbeschattung der Geometrie) berücksichtigen. Wir können beide Fälle mit der Smith-Methode betrachten :

$$

$$G (n, v, l, k) = G_ {sub} (n, v, k) G_ {sub} (n, l, k)$$

Verwendung der Smith-Methode mit Schlick-GGX als $$$G_ {sub}$ ergibt folgendes Bild mit unterschiedlicher Rauheit R:

Die Geometriefunktion ist ein Faktor zwischen [0.0, 1.0], wobei Weiß (oder 1.0) keine Schattierung der Mikroflächen bedeutet und Schwarz (oder 0.0) eine vollständige Schattierung der Mikroflächen bedeutet.

In GLSL wird eine Geometriefunktion in den folgenden Code konvertiert:

 float GeometrySchlickGGX(float NdotV, float k) { float nom = NdotV; float denom = NdotV * (1.0 - k) + k; return nom / denom; } float GeometrySmith(vec3 N, vec3 V, vec3 L, float k) { float NdotV = max(dot(N, V), 0.0); float NdotL = max(dot(N, L), 0.0); float ggx1 = GeometrySchlickGGX(NdotV, k); float ggx2 = GeometrySchlickGGX(NdotL, k); return ggx1 * ggx2; } 

Fresnel-Gleichung

Die Fresnel-Gleichung beschreibt das Verhältnis von reflektiertem und gebrochenem Licht, das von dem Winkel abhängt, unter dem wir die Oberfläche betrachten. Wenn Licht auf eine Oberfläche trifft, gibt uns die Fresnel-Gleichung den Prozentsatz des reflektierten Lichts basierend auf dem Winkel, unter dem wir diese Oberfläche sehen. Aus diesem Reflexionsverhältnis und dem Energieerhaltungsgesetz können wir direkt den gebrochenen Teil des Lichts erhalten, der gleich der verbleibenden Energie ist.

Jede Oberfläche oder jedes Material weist ein Grundreflexionsvermögen auf , das beim direkten Betrachten der Oberfläche beobachtet wird. Wenn Sie jedoch die Oberfläche in einem Winkel betrachten, werden alle Reflexionen deutlicher. Sie können dies selbst überprüfen, indem Sie Ihren senkrechten Holz- oder Metalltisch zuerst senkrecht und dann in einem Winkel von nahezu 90 Grad betrachten. Sie werden sehen, dass Reflexionen viel deutlicher werden. Theoretisch reflektieren alle Oberflächen das Licht vollständig, wenn sie von ihnen in einem idealen Winkel von 90 Grad betrachtet werden. Dieser Effekt wird als Fresnel bezeichnet und durch die Fresnel-Gleichung beschrieben .

Die Fresnel-Gleichung ist recht komplex, kann aber glücklicherweise mit der Fresnel-Schlick-Näherung vereinfacht werden:

$$

$$F_ {Schlick} (h, v, F_0) = F_0 + (1 - F_0) (1 - (h \ cdot v)) ^ 5$$

$$$F_0$ stellt das grundlegende Reflexionsvermögen der Oberfläche dar, das wir unter Verwendung von sogenannten Brechungsindizes oder IORs (Brechungsindizes) berechnen. Wie Sie auf der Oberfläche der Kugel sehen können, ist die Blickrichtung näher an den Grenzen der sichtbaren Kugel (dem Winkel zwischen der Blickrichtung und dem Median), wie Sie auf der Oberfläche der Kugel sehen können 90 ), , , :

, . , - . (), , . , ( $$$F_0$ ) ( 0 , ) -, , .

. , , :

: 0.17, , , ( ) 0.5 1.0. , “”, $$$F_0$ RGB ( ).

, metallic workflow: , (metalness), , .

: , ; , . , 0.0 1.0. - , , , . , .

$$$F_0$ , , - , , . :

 vec3 F0 = vec3(0.04); F0 = mix(F0, surfaceColor.rgb, metalness); 

, . , $$$F_0$ . 0.04 . , , , F0 . , , .

- :

 vec3 fresnelSchlick(float cosTheta, vec3 F0) { return F0 + (1.0 - F0) * pow(1.0 - cosTheta, 5.0); } 

cosTheta .

-

BRDF - :

$$

$$L_o(p,\omega_o)=\int\limits_\Omega(k_d\frac{c}{\pi}+k_s\frac{DFG}{4(\omega_o\cdot n)(\omega_i \cdot n)}) L_i(p, \omega_i)n\cdot \omega_i d\omega_i$$

. , , F . $$$k_s$ , , $$$k_s$ . , :

$$

$$L_o(p,\omega_o)=\int\limits_\Omega(k_d\frac{c}{\pi}+\frac{DFG}{4(\omega_o\cdot n)(\omega_i \cdot n)}) L_i(p, \omega_i)n\cdot \omega_i d\omega_i$$

, PBR. , , . , , .

PBR

, PBR, , , PBR. , PBR, . , : , .

, PBR, :

: , . , . , ; .

: , , . , , .

: . , PBR-, , : .

: , . . , . PBR- , , (1.0 — ) .

AO (ambient occlusion) : AO . , , . AO , . . , 3D-.

. PBR, , . , PBR, PBR-, , , .

Verwandte Materialien

• Background: Physics and Math of Shading by Naty Hoffmann: , , ; PBR, must-read .
• Real shading in Unreal Engine 4 : PBR, Epic Games Unreal Engine 4. PBR, , .
• Marmoset: PBR Theory : PBR. , , , .
• Coding Labs: Physically based rendering : , PBR.
• Coding Labs: Physically Based Rendering — Cook–Torrance : BRDF -
• Wolfire Games — Physically based rendering : PBR Lukas Orsvärn.
• [SH17C] Physically Based Shading : shadertoy (: ) Krzysztof Narkowi, PBR.