Das Prinzip der geringsten Aktion. Teil 2

Das letzte Mal haben wir kurz eines der bemerkenswertesten physikalischen Prinzipien untersucht - das Prinzip der geringsten Handlung - und uns auf ein Beispiel geeinigt, das anscheinend dem widerspricht. In diesem Artikel werden wir uns ausführlicher mit diesem Prinzip befassen und sehen, was in diesem Beispiel passiert.

Diesmal brauchen wir etwas mehr Mathe. Ich werde jedoch versuchen, den Hauptteil des Artikels noch einmal auf elementarer Ebene darzulegen. Ich werde etwas strengere und komplexere Punkte hervorheben, die unbeschadet des Grundverständnisses des Artikels übersprungen werden können.

Randbedingungen

Wir beginnen mit dem einfachsten Objekt - einem Ball, der sich frei im Raum bewegt und auf den keine Kräfte wirken. Eine solche Kugel bewegt sich bekanntlich gleichmäßig und geradlinig. Nehmen wir zur Vereinfachung an, dass es sich entlang der Achse bewegt $$$x$ ::

Um seine Bewegung genau zu beschreiben, werden in der Regel Anfangsbedingungen angegeben. Zum Beispiel wird festgelegt, dass zum anfänglichen Zeitpunkt $$$t_A$ Der Ball war an einem Punkt $$$A$ mit Koordinate $$$x_A$ und hatte Geschwindigkeit $$$v_A$ . Nachdem wir die Anfangsbedingungen in dieser Form festgelegt haben, bestimmen wir eindeutig die weitere Bewegung des Balls - er bewegt sich mit konstanter Geschwindigkeit und seiner Position zu der Zeit $$$t$ ist gleich der Ausgangsposition plus der Geschwindigkeit multipliziert mit der verstrichenen Zeit: $$$x (t) = x_A + v_A \ cdot (t-t_A)$ . Diese Art der Einstellung der Anfangsbedingungen ist sehr natürlich und intuitiv vertraut. Wir haben zu Beginn alle notwendigen Informationen über die Bewegung des Balls abgefragt, und dann wird seine Bewegung durch Newtons Gesetze bestimmt.

Dies ist jedoch nicht die einzige Möglichkeit, die Bewegung des Balls festzulegen. Eine andere Alternative besteht darin, die Position des Balls zu zwei verschiedenen Zeitpunkten einzustellen. $$$t_A$ und $$$t_B$ . Das heißt, frage das:

1) zum Zeitpunkt $$$t_A$ Der Ball war an einem Punkt $$$A$ (mit Koordinate $$$x_A$ );
2) zum Zeitpunkt $$$t_B$ Der Ball war an einem Punkt $$$B$ (mit Koordinate $$$x_B$ )

Der Ausdruck "war an einem Punkt $$$A$ "Bedeutet nicht, dass der Ball an einem Punkt ruhte $$$A$ . Zur Zeit $$$t_A$ er konnte über einen Punkt fliegen $$$A$ . Es bedeutet, dass seine Position zur Zeit $$$t_A$ fiel mit einem Punkt zusammen $$$A$ . Gleiches gilt für den Punkt $$$B$ .

Diese beiden Bedingungen bestimmen auch eindeutig die Bewegung des Balls. Seine Bewegung ist leicht zu berechnen. Um beide Bedingungen zu erfüllen, muss die Geschwindigkeit des Balls offensichtlich sein $$$(x_B-x_A) / (t_B-t_A)$ . Ballposition zur Zeit $$$t$ ist wieder gleich der Ausgangsposition plus der Geschwindigkeit multipliziert mit der verstrichenen Zeit:

$$

$$x (t) = x_A + ((x_B-x_A) / (t_B-t_A)) \ cdot (t-t_A)$$

Beachten Sie, dass wir unter den Bedingungen des Problems die Anfangsgeschwindigkeit nicht einstellen mussten. Sie wird eindeutig aus den Bedingungen 1) und 2) bestimmt.

Das Einstellen der Bedingungen auf die zweite Weise sieht ungewöhnlich aus. Vielleicht ist nicht klar, warum es im Allgemeinen notwendig sein kann, sie in dieser Form zu fragen. Im Prinzip der geringsten Wirkung werden jedoch genau die Bedingungen in den Formen 1) und 2) verwendet und nicht in Form der Einstellung der Anfangsposition und der Anfangsgeschwindigkeit.

Flugbahn der geringsten Aktion

Lassen Sie uns nun ein wenig von der tatsächlichen freien Bewegung des Balls abweichen und das folgende rein mathematische Problem betrachten. Angenommen, wir haben einen Ball, den wir manuell bewegen können, wie wir wollen. In diesem Fall müssen wir die Bedingungen 1) und 2) erfüllen. Das heißt, dazwischen $$$t_A$ und $$$t_B$ wir müssen es von dem Punkt bewegen $$$A$ auf den Punkt $$$B$ . Dies kann auf ganz andere Weise erfolgen. Jede solche Methode wird als Flugbahn des Balls bezeichnet und kann durch die Funktion der Position des Balls zur Zeit beschrieben werden $$$x (t)$ . Verschieben wir einige dieser Trajektorien auf das Diagramm der Abhängigkeit der Ballposition von der Zeit:

Zum Beispiel können wir den Ball mit der gleichen Geschwindigkeit bewegen wie $$$(x_B-x_A) / (t_B-t_A)$ (grüner Weg). Oder wir können es auf dem halben Punkt halten $$$A$ und dann doppelte Geschwindigkeit, um zum Punkt zu gelangen $$$B$ (blaue Flugbahn). Sie können es zuerst in die entgegengesetzte Richtung bewegen. $$$B$ Seite und dann schon zu bewegen $$$B$ (braune Flugbahn). Sie können es hin und her bewegen (rote Flugbahn). Im Allgemeinen können Sie es beliebig verschieben, wenn nur die Bedingungen 1) und 2) eingehalten werden.

Für jede solche Flugbahn können wir eine Zahl abgleichen. In unserem Beispiel, d.h. Wenn keine auf den Ball einwirkenden Kräfte vorhanden sind, entspricht diese Zahl der gesamten akkumulierten kinetischen Energie für die gesamte Zeit ihrer Bewegung im Intervall zwischen $$$t_A$ und $$$t_B$ und heißt eine Aktion.

In diesem Fall vermittelt das Wort "akkumulierte" kinetische Energie die Bedeutung nicht genau. In der Realität sammelt sich die kinetische Energie nirgendwo an, die Akkumulation wird nur zur Berechnung der Aktion für die Flugbahn verwendet. In der Mathematik gibt es für eine solche Akkumulation ein sehr gutes Konzept - das Integral:

$$

$$S = \ int \ limit_ {t_A} ^ {t_B} Tdt$$

Die Aktion wird normalerweise durch den Buchstaben angezeigt $$$S$ . Symbol $$$T$ bedeutet kinetische Energie. Dieses Integral bedeutet, dass die Aktion gleich der akkumulierten kinetischen Energie des Balls über einen Zeitraum von ist $$$t_A$ vorher $$$t_B$ .

Nehmen wir als Beispiel einen Ball mit einem Gewicht von 1 kg. Legen Sie einige Randbedingungen fest und berechnen Sie die Aktion für zwei verschiedene Flugbahnen. Lass den Punkt $$$B$ ist 1 Meter vom Punkt entfernt $$$A$ und Zeit $$$t_B$ von der Zeit entfernt $$$t_A$ für 1 Sekunde. Das heißt, Wir müssen den Ball bewegen, der zu Beginn der Zeit am Punkt war $$$A$ in einer Sekunde in einem Abstand von 1 m entlang der Achse $$$x$ .

Im ersten Beispiel (grüne Flugbahn) haben wir den Ball gleichmäßig bewegt, d.h. mit der gleichen Geschwindigkeit, die natürlich gleich sein sollte: $$$v = 1$ m / s Die kinetische Energie des Balls zu jedem Zeitpunkt ist gleich: $$$T = mv ^ 2/2$ = 1/2 J. In einer Sekunde sammelt sich 1/2 J. $$$\ cdot$ mit kinetischer Energie. Das heißt, gültig für eine solche Flugbahn ist: $$$S = 1/2$ J. $$$\ cdot$ s

Lassen Sie uns jetzt den Ball nicht sofort vom Punkt übertragen $$$A$ auf den Punkt $$$Bis$ und halten Sie es eine halbe Sekunde lang an einem Punkt $$$A$ und dann übertragen wir es für die verbleibende Zeit gleichmäßig auf den Punkt $$$B$ . In der ersten halben Sekunde ruht der Ball und seine kinetische Energie ist Null. Daher ist der Beitrag zur Wirkung dieses Teils der Flugbahn ebenfalls gleich Null. In der zweiten halben Sekunde übertragen wir den Ball mit doppelter Geschwindigkeit: $$$v = 2$ m / s Die kinetische Energie ist gleich $$$T = mv ^ 2/2$ = 2 J. Der Beitrag dieser Zeitspanne zur Aktion beträgt 2 J multipliziert mit einer halben Sekunde, d.h. 1 J. $$$\ cdot$ s Daher ist die allgemeine Aktion für eine solche Flugbahn gleich $$$S = 1$ J. $$$\ cdot$ s

In ähnlicher Weise entspricht jede andere Trajektorie mit den angegebenen Randbedingungen 1) und 2) einer bestimmten Zahl, die der Aktion für eine gegebene Trajektorie entspricht. Unter all diesen Trajektorien gibt es eine Trajektorie, bei der die Aktion am geringsten ist. Es kann bewiesen werden, dass diese Trajektorie eine grüne Trajektorie ist, d.h. gleichmäßige Bewegung des Balls. Für jede andere Flugbahn, egal wie schwierig sie ist, beträgt die Aktion mehr als die Hälfte.

In der Mathematik wird ein solcher Vergleich für jede Funktion einer bestimmten Zahl als Funktion bezeichnet. Sehr oft entstehen in Physik und Mathematik Aufgaben wie unsere, d.h. um eine Funktion zu finden, für die der Wert einer bestimmten Funktion minimal ist. Eine der Aufgaben von großer historischer Bedeutung für die Entwicklung der Mathematik ist beispielsweise das Problem der Bachistochron . Das heißt, Finden einer Kurve, entlang der der Ball am schnellsten rollt. Auch hier kann jede Kurve durch die Funktion h (x) dargestellt werden, und jeder Funktion kann eine Zahl zugewiesen werden, in diesem Fall die Ballrollzeit. Wiederum läuft das Problem darauf hinaus, eine Funktion zu finden, für die der Wert der Funktion minimal ist. Der Bereich der Mathematik, der sich mit solchen Problemen befasst, wird als Variationsrechnung bezeichnet.

Prinzip der geringsten Aktion

In den oben diskutierten Beispielen haben wir zwei spezielle Trajektorien, die auf zwei verschiedene Arten erhalten werden.

Die erste Flugbahn ergibt sich aus den Gesetzen der Physik und entspricht der realen Flugbahn einer freien Kugel, die von keinen Kräften beeinflusst wird und für die Randbedingungen in den Formen 1) und 2) angegeben sind.

Die zweite Trajektorie ergibt sich aus dem mathematischen Problem, eine Trajektorie mit gegebenen Randbedingungen 1) und 2) zu finden, für die die Aktion minimal ist.

Das Prinzip der geringsten Aktion besagt, dass diese beiden Trajektorien zusammenfallen müssen. Mit anderen Worten, wenn bekannt ist, dass sich der Ball so bewegt hat, dass die Randbedingungen 1) und 2) erfüllt sind, dann hat er sich notwendigerweise entlang eines Pfades bewegt, für den die Aktion im Vergleich zu jedem anderen Pfad mit denselben Randbedingungen minimal ist.

Man könnte dies als bloßen Zufall betrachten. Es gibt viele Probleme, bei denen einheitliche Flugbahnen und gerade Linien auftreten. Das Prinzip der geringsten Wirkung ist jedoch ein sehr allgemeines Prinzip, das in anderen Situationen gilt, beispielsweise für die Bewegung des Balls in einem gleichmäßigen Gravitationsfeld. Dazu müssen Sie nur die kinetische Energie durch die Differenz zwischen kinetischer und potentieller Energie ersetzen. Diese Differenz wird als Lagrange- oder Lagrange-Funktion bezeichnet, und die Aktion wird jetzt gleich der gesamten akkumulierten Lagrange-Funktion. Tatsächlich enthält die Lagrange-Funktion alle erforderlichen Informationen zu den dynamischen Eigenschaften des Systems.

Wenn wir einen Ball in einem gleichmäßigen Schwerefeld starten, so dass er einen Punkt passiert $$$A$ zur Zeit $$$t_A$ und flog auf den Punkt $$$B$ zur Zeit $$$t_B$ dann wird er nach Newtons Gesetzen eine Parabel fliegen. Es ist diese Parabel, die mit den Trajektorien übereinstimmt, für die die Aktion minimal sein wird.

Für einen Körper, der sich in einem potentiellen Feld bewegt, beispielsweise im Gravitationsfeld der Erde, ist die Lagrange-Funktion also gleich: $$$L = T (v) -V (x, y, z)$ . Kinetische Energie $$$T$ hängt von der Geschwindigkeit des Körpers und dem Potential ab - von seiner Position, d.h. Koordinaten $$$x, y, z$ . In der analytischen Mechanik wird der gesamte Koordinatensatz, der die Position eines Systems bestimmt, normalerweise mit einem Buchstaben bezeichnet $$$q$ . Für einen Ball, der sich in einem Gravitationsfeld frei bewegt, $$$q$ bedeutet Koordinaten $$$x$ , $$$y$ und $$$z$ .

Um die Änderungsrate einer Größe anzuzeigen, setzen sie in der Physik dieser Größe sehr oft einfach ein Ende. Zum Beispiel $$$\ dot x$ gibt die Änderungsrate der Koordinate an $$$x$ oder mit anderen Worten die Geschwindigkeit des Körpers in der Richtung $$$x$ . Unter Verwendung dieser Konventionen wird die Geschwindigkeit unseres Balls in der analytischen Mechanik als bezeichnet $$$\ dot q$ . Das heißt, $$$\ dot q$ Komponenten der mittleren Geschwindigkeit $$$v_x, v_y, v_z$ .

Da die Lagrange-Funktion von Geschwindigkeit und Koordinaten abhängt, kann sie auch explizit von der Zeit abhängen (explizit von der Zeit abhängig bedeutet, dass der Wert $$$L$ zu verschiedenen Zeitpunkten, unterschiedlich, bei gleichen Geschwindigkeiten und Positionen des Balls) dann wird die Aktion in allgemeiner Form geschrieben als

$$

$$S = \ int \ limit_ {t_A} ^ {t_B} L (\ dot q, q, t) dt$$

Nicht immer minimal

Am Ende des vorherigen Teils haben wir uns jedoch ein Beispiel angesehen, bei dem das Prinzip der geringsten Aktion eindeutig nicht funktioniert. Dazu haben wir wieder einen freien Ball genommen, der von keinen Kräften beeinflusst wird, und eine Federwand daneben platziert.
Wir setzen die Randbedingungen so, dass die Punkte $$$A$ und $$$B$ zusammenpassen. Das heißt, und zur Zeit $$$t_A$ und zur Zeit $$$t_B$ Der Ball sollte am selben Punkt sein $$$A$ . Eine der möglichen Flugbahnen ist das Stehen des Balls an Ort und Stelle. Das heißt, die ganze Zeit dazwischen $$$t_A$ und $$$t_B$ er wird an einem Punkt stehen $$$A$ . Die kinetische und potentielle Energie ist in diesem Fall gleich Null, daher ist die Aktion für eine solche Trajektorie auch gleich Null.

Genau genommen kann potentielle Energie nicht gleich Null, sondern einer beliebigen Zahl genommen werden, da der Unterschied in der potentiellen Energie an verschiedenen Punkten im Raum wichtig ist. Eine Änderung des Wertes der potentiellen Energie wirkt sich jedoch nicht auf die Suche nach einer Flugbahn mit minimaler Wirkung aus. Es ist nur so, dass sich für alle Trajektorien der Wert der Aktion um dieselbe Zahl ändert und die Trajektorie mit minimaler Aktion die Trajektorie mit minimaler Aktion bleibt. Der Einfachheit halber wählen wir für unseren Ball die potentielle Energie gleich Null.

Eine andere mögliche physikalische Flugbahn mit den gleichen Randbedingungen wäre eine Flugbahn, bei der der Ball zuerst nach rechts fliegt und einen Punkt passiert $$$A$ zur Zeit $$$t_A$ . Dann kollidiert er mit der Feder, drückt sie zusammen, die Feder richtet sich auf, drückt den Ball zurück und fliegt wieder an der Spitze vorbei $$$A$ . Sie können die Geschwindigkeit des Balls so wählen, dass er von der Wand abprallt und einen Punkt fliegt $$$A$ genau im Moment $$$t_B$ . Die Aktion mit dieser Flugbahn entspricht im Wesentlichen der akkumulierten kinetischen Energie während des Fluges zwischen dem Punkt $$$A$ und Wand und Rücken. Es wird eine bestimmte Zeitspanne geben, in der der Ball die Feder zusammendrückt und ihre potentielle Energie zunimmt, und während dieser Zeitspanne wird die potentielle Energie einen negativen Beitrag zur Aktion leisten. Ein solcher Zeitraum wird jedoch nicht sehr groß sein und die Aktion wird sich nicht wesentlich verringern.



Die Abbildung zeigt beide physikalisch möglichen Flugbahnen des Balls. Der grüne Pfad entspricht einer Kugel in Ruhe, während der blaue einer Kugel entspricht, die von der Federwand abprallt.

Allerdings hat nur einer von ihnen eine minimale Wirkung, nämlich der erste! Die zweite Flugbahn hat mehr Action. Es stellt sich heraus, dass es bei diesem Problem zwei physikalisch mögliche Trajektorien gibt und nur eine mit minimaler Wirkung. Das heißt, In diesem Fall funktioniert das Prinzip der geringsten Aktion nicht.

Stationäre Punkte

Um zu verstehen, worum es hier geht, lassen Sie uns zunächst vom Prinzip der geringsten Aktion abweichen und die üblichen Funktionen übernehmen. Nehmen wir eine Funktion $$$y (x)$ und zeichne ihren Zeitplan:

In der Grafik habe ich vier Sonderpunkte grün markiert. Was haben diese Punkte gemeinsam? Stellen Sie sich vor, ein Funktionsgraph ist eine echte Folie, auf der ein Ball rollen kann. Die vier markierten Punkte sind insofern besonders, als wenn Sie den Ball genau an diesem Punkt installieren, er nirgendwo rollt. An allen anderen Punkten, zum Beispiel an Punkt E, kann er nicht an Ort und Stelle bleiben und beginnt zu rutschen. Solche Punkte werden stationär genannt. Das Finden solcher Punkte ist eine nützliche Aufgabe, da jedes Maximum oder Minimum der Funktion, wenn sie keine scharfen Knicke aufweist, ein stationärer Punkt sein muss.

Wenn wir diese Punkte genauer klassifizieren, ist Punkt A das absolute Minimum der Funktion, d.h. Sein Wert ist kleiner als jeder andere Funktionswert. Punkt B - ist weder ein Maximum noch ein Minimum und wird als Sattelpunkt bezeichnet. Punkt C wird als lokales Maximum bezeichnet, d.h. Der Wert darin ist größer als an benachbarten Punkten der Funktion. Und Punkt D ist ein lokales Minimum, d.h. Der Wert darin ist kleiner als an benachbarten Punkten der Funktion.

Die Suche nach solchen Punkten wird von einem Zweig der Mathematik durchgeführt, der als mathematische Analyse bezeichnet wird. Auf andere Weise wird es manchmal als Infinitesimalanalyse bezeichnet, da es weiß, wie man mit infinitesimalen Größen arbeitet. Aus Sicht der mathematischen Analyse haben stationäre Punkte eine besondere Eigenschaft, dank derer sie gefunden werden. Um zu verstehen, was diese Eigenschaft ist, müssen wir verstehen, wie die Funktion in sehr kleinen Abständen von diesen Punkten aussieht. Dazu nehmen wir ein Mikroskop und betrachten es an unseren Punkten. Die Abbildung zeigt, wie die Funktion in der Nähe verschiedener Punkte bei unterschiedlichen Vergrößerungen aussieht.

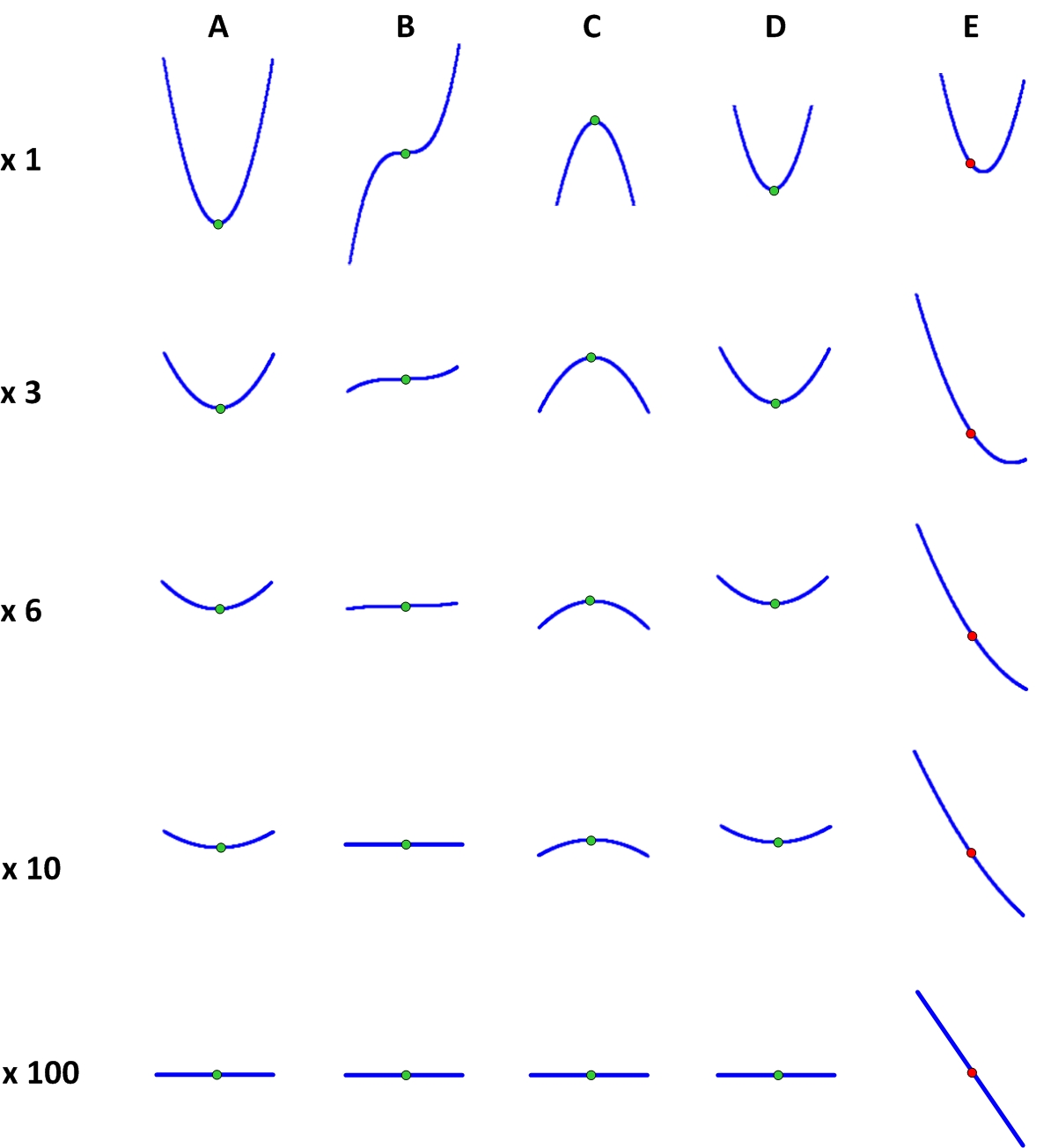
Es ist ersichtlich, dass bei einer sehr großen Vergrößerung (d. H. Bei sehr kleinen Abweichungen x) die stationären Punkte genau gleich aussehen und sich stark von dem nicht stationären Punkt unterscheiden. Es ist leicht zu verstehen, was dieser Unterschied ist: Der Graph der Funktion an einem stationären Punkt mit zunehmender Größe wird zu einer streng horizontalen Linie, und in einem instationären Punkt wird er zu einer geneigten Linie. Deshalb rollt eine an einem stationären Punkt montierte Kugel nicht.

Die Horizontalität der Funktion am stationären Punkt kann unterschiedlich ausgedrückt werden: Die Funktion am stationären Punkt ändert sich praktisch nicht mit einer sehr geringen Änderung ihres Arguments $$$x$ sogar im Vergleich zum Argument selbst. Die Funktion befindet sich mit einer kleinen Änderung an einem instationären Punkt $$$x$ variiert im Verhältnis zu $$$x$ . Und je größer der Winkel der Funktion ist, desto stärker ändert sich die Funktion beim Ändern $$$x$ . Tatsächlich wird die Funktion mit zunehmender Größe der Tangente an den Graphen an dem fraglichen Punkt immer ähnlicher.

In der strengen mathematischen Sprache ändert sich der Ausdruck „Funktion praktisch nicht an einem Punkt $$$x_0$ mit sehr wenig Veränderung $$$x$ "Bedeutet, dass das Verhältnis der Funktionsänderung und der Änderung seines Arguments $$$Δy / Δx$ tendiert zu 0 bei $$$∆x$ Tendenz zu 0:

$$$$ Anzeige $$ \ lim_ {Δx \ bis 0} \ frac {Δy (x_0)} {Δx} = \ lim_ {x \ bis 0} \ frac {y (x_0 + Δx) -y (x_0) } {∆x} = 0 $$ display $$

Für einen instationären Punkt tendiert dieses Verhältnis zu einer Zahl ungleich Null, die gleich der Steigung der Funktion an diesem Punkt ist. Die gleiche Zahl wird als Ableitung der Funktion an einem bestimmten Punkt bezeichnet. Die Ableitung der Funktion zeigt, wie schnell sich die Funktion in der Nähe eines bestimmten Punktes mit einer kleinen Änderung ihres Arguments ändert $$$x$ . Stationäre Punkte sind also Punkte, an denen die Ableitung der Funktion 0 ist.

Stationäre Flugbahnen

In Analogie zu stationären Punkten kann das Konzept der stationären Trajektorien eingeführt werden. Es sei daran erinnert, dass jede Flugbahn einem bestimmten Aktionswert entspricht, d.h. eine Nummer. Dann kann es eine solche Trajektorie geben, dass sich für Trajektorien in der Nähe mit denselben Randbedingungen die entsprechenden Aktionswerte praktisch nicht von der Aktion für die stationäre Trajektorie selbst unterscheiden. Eine solche Flugbahn nennt man stationär. Mit anderen Worten, jede Flugbahn in der Nähe von stationär hat einen Aktionswert, der sich sehr wenig von der Aktion für diese stationäre Flugbahn unterscheidet.

Wiederum hat in der mathematischen Sprache "wenig anders" die folgende genaue Bedeutung. Nehmen wir an, wir haben eine funktionale $$$S (x (t))$ für Funktionen mit den erforderlichen Randbedingungen 1) und 2), d.h. $$$x (t_A) = A$ und $$$x (t_B) = B$ . Angenommen, die Flugbahn $$$x (t)$ - stationär.

Wir können jede andere Funktion übernehmen. $$$g (t)$ so dass es an den Enden Nullwerte annimmt, d.h. $$$g (t_A)$ = $$$g (t_B)$ = 0. Nehmen Sie auch die Variable $$$ε$ was wir immer weniger tun werden. Von diesen beiden Funktionen und Variablen $$$ε$ wir können eine dritte Funktion machen $$$x '(t) = x (t) + εg (t)$ , $$$f'(t_A)=A$ und $$$f'(t_B)=B$ . $$$ε$ , $$$x'(t)$ , $$$x(t)$ .

$$$ε$ $$$x'(t)$ $$$x(t)$ $$$ε$ . Das heißt,

$$

$$\lim_{ε \to 0} \frac {S(x'(t))-S(x(t))}ε=\lim_{ε \to 0} \frac {S(x(t)+εg(t))-S(x(t))}ε = 0$$

$$$g(t)$ , $$$g(t_A)$ = $$$g(t_B)$ = 0.

(, , ) $$$δS$ . «» « ».

$$$δS=0$ .

Die Methode, stationäre Funktionen zu finden (nicht nur für das Prinzip der geringsten Wirkung, sondern auch für viele andere Probleme), wurde von zwei Mathematikern gefunden - Euler und Lagrange. Es stellt sich heraus, dass die stationäre Funktion, deren Funktion durch ein dem Aktionsintegral ähnliches Integral ausgedrückt wird, eine bestimmte Gleichung erfüllen muss, die nun als Euler-Lagrange-Gleichung bezeichnet wird.

Stationäres Prinzip

Die Situation mit einem Minimum an Aktion für Trajektorien ist ähnlich der Situation mit einem Minimum an Funktionen für Funktionen. Damit die Flugbahn den geringsten Effekt hat, muss sie eine stationäre Flugbahn sein. Es sind jedoch nicht alle stationären Trajektorien Trajektorien mit minimaler Aktion. Beispielsweise kann eine stationäre Flugbahn lokal nur eine minimale Wirkung haben. Das heißt,seine Wirkung ist geringer als die einer anderen benachbarten Flugbahn. Irgendwo weit weg kann es jedoch andere Flugbahnen geben, für die die Aktion noch geringer sein wird.

Es stellt sich heraus, dass sich reale Körper nicht unbedingt mit der geringsten Aktion auf Flugbahnen bewegen müssen. Sie können sich entlang eines größeren Satzes spezieller Trajektorien bewegen, nämlich stationärer Trajektorien. Das heißt,Die reale Flugbahn des Körpers wird immer stationär sein. Daher wird das Prinzip der geringsten Aktion korrekter als das Prinzip der stationären Aktion bezeichnet. Nach der etablierten Tradition wird es jedoch oft als das Prinzip der geringsten Aktion bezeichnet, was nicht nur eine Minimalität, sondern auch eine Stationarität der Flugbahnen impliziert.

Jetzt können wir das Prinzip des stationären Handelns in einer mathematischen Sprache aufschreiben, wie es normalerweise in Lehrbüchern geschrieben wird:

$$

$$δS=δ\int\limits_{t_A}^{t_B} L(\dot q,q,t)dt = 0$$

.

Hier $$$q$Sind verallgemeinerte Koordinaten, d.h. Eine Reihe von Variablen, die die Position des Systems eindeutig angeben.
$$$\dot q$ - die Änderungsrate der verallgemeinerten Koordinaten.
$$$L(\dot q,q,t)$ - die Lagrange-Funktion, die von den verallgemeinerten Koordinaten, ihren Geschwindigkeiten und möglicherweise der Zeit abhängt.
$$$S$ - eine Aktion, die von der spezifischen Flugbahn des Systems abhängt (d. H. $$$q(t)$ )

Die realen Trajektorien des Systems sind stationär, d.h. für sie eine Variation der Aktion$$$δS=0$ .

Wenn wir mit einer Kugel und einer elastischen Wand zum Beispiel zurückkehren, wird die Erklärung dieser Situation jetzt sehr einfach. Angesichts der Randbedingungen, die der Ball auch während haben sollte$$$t_A$ und während $$$t_B$ auf den Punkt kommen $$$A$ . . , . , , . .

( ) , .