
Wahrscheinlich haben Sie eine vernünftige Frage: Warum?
Aus pragmatischer Sicht besteht keine Notwendigkeit.) Sie können immer bedingtes Wolfram verwenden. Wenn Sie dies in Python tun müssen, verwenden Sie spezielle Module, die nicht so schwer zu beherrschen sind.
Aber wenn Sie plötzlich eine solche Aufgabe erhalten haben oder einfach nur gerne programmieren, wie ich, dann haben Sie aufregende - und manchmal nicht sehr - Stunden Zeit, um ein Programm zu schreiben und es zu debuggen.
Wenn wir dieses Meisterwerk schreiben, müssen wir wirklich Schritt für Schritt debuggen. Laden Sie daher PyCharm, VS oder etwas anderes mit dieser Funktion herunter. Für das Erstellen von Tabellen ist das Fehlen dieser Funktion nicht so kritisch, sondern für das Zeichnen ...
Also, was wird mein Programm sein. Bei der Eingabe werden drei Werte angenommen: der Anfang und das Ende des Segments, auf dem wir unsere Funktion sehen möchten, und der Schritt, mit dem wir uns bewegen werden. Als nächstes zeichnen wir an jedem Punkt eine Tabelle mit Funktionswerten aus dem durch die Eingabedaten angegebenen Wertebereich. Nun, dann zeichnen wir den Graphen der Funktion selbst mit der sich bewegenden y-Achse.
Also lass uns gehenZunächst werde ich einige Funktionen deklarieren, deren Werte wir berücksichtigen werden. Ich nehme es ganz einfach
from math import sqrt def y1(x): return x**3 - 2*x**2 + 4*x - 8 def y2(x): return 1 - 1/x**2 def y3(x): return sqrt(abs(y1(x)*y2(x)))
Jetzt haben wir drei Funktionen, von denen zwei einen Haltepunkt haben. Aus dem Mathematikmodul, in dem alle mathematischen Brötchen (einschließlich Kosinus, Arkustangens und anderer Trigonometrie) gespeichert sind, importieren wir sqrt, dh die Quadratwurzel. Wir brauchen es, um die Funktion y3 zu lesen.
Danach müssen wir den Funktionsbereich durch x und den Schritt lesen, mit dem wir diesen Bereich durchlaufen. Dafür werde ich Karte verwenden.
Als ersten Parameter nimmt diese Funktion eine Funktion an, die die benötigten Daten irgendwie transformiert, und als zweites Argument eine Art Datenblatt, das wir verarbeiten müssen
from_x, to_x, pace_x = map(float, input("Enter the first and the last"\ " x-coordinates and a pace dividing them by a"\ " space:").split())
Wir lesen die drei durch ein Leerzeichen eingegebenen Werte und teilen sie durch ein Leerzeichen in Elemente (mit der Split-Methode, die beim Aufrufen ohne Parameter die von Ihnen angegebene Zeichenfolge automatisch durch Leerzeichen teilt). Die mit input () eingegebenen Daten sind standardmäßig vom Typ str, dh eine Zeichenfolge, sodass hier keine Fehler auftreten.
Da die Bereichsgrenzzahlen gebrochen sein können, konvertieren wir jedes Element des resultierenden Arrays mithilfe der Float-Funktion in eine reelle Zahl.
Beachten Sie, dass Variablen ohne Angabe eines Datentyps deklariert werden. Sie wird automatisch ermittelt (der Datentyp des Werts, den Sie einer Variablen zuweisen möchten) oder mithilfe der Funktionen str, int, float usw. manuell durch Variablen festgelegt, wobei dieselben Funktionen auf die Werte angewendet werden. Dieselbe Variable kann im gesamten Programm einen anderen Datentyp haben - weisen Sie ihr einfach einen neuen Wert mit einem anderen Datentyp zu.
Zum Beispiel
auxiliary_variable = ""
Kehren wir zu unserem Programm zurück. Wir müssen überprüfen, ob die eingegebenen Daten korrekt sind.
Das Programm sollte drucken, dass die eingegebenen Daten falsch sind, wenn:
- Schritt ist 0
- Die untere Grenze des Bereichs ist größer als die obere und der Schritt ist positiv ( dh wir haben eine arithmetische Folge der Form xn = von_x + Tempo_x * (n - 1) , in der von_x> bis_x . Da Tempo_x> 0 ist, wird diese Folge zunehmen und wir nie zu_x kommen )
- Die Untergrenze des Bereichs ist kleiner als die Obergrenze, und der Schritt ist negativ (ähnliche Argumentation).
- Graphen, die aus einem Punkt bestehen, sind nicht informativ, daher muss das Segment, auf dem wir die Funktion konstruieren, mindestens zwei Werte enthalten
Wir formulieren diese Bedingungen im Code. Offensichtlich ist der erste Punkt einfach einzustellen. Das zweite und dritte können zu einem kombiniert werden, wenn Sie feststellen, dass das Vorzeichen der Differenz zwischen dem ersten (from_x) und dem letzten (to_x) mit dem Schrittzeichen übereinstimmen sollte. Nun, der vierte Punkt ist auch nicht so kompliziert: Der Modul der Differenz zwischen dem ersten und dem letzten Wert sollte nicht kleiner sein als das Schrittmodul.
Aufgrund des Moduls kann es vorkommen, dass die Vorzeichen des Unterschieds und des Schritts nicht zusammenfallen, die zweite Bedingung diese Fälle jedoch abschneidet, sodass die Bedingung korrekt ist.
Infolgedessen sehen diese drei Bedingungen folgendermaßen aus:
if (pace_x != 0) and (to_x - from_x)*pace_x >= 0 and abs(to_x - from_x):
Wir gehen direkt zum Tisch. Um das Debuggen zu vereinfachen, werde ich mehrere Variablen mit sprechenden Namen erstellen, die für die Genauigkeit der Zahlen, die Anzahl der Leerzeichen vor der Nummer, die Anzahl der Leerzeichen nach der Nummer usw. verantwortlich sind.
dials_precision = "%10.6g"
Also, was ist hier los?

dials_precision = "%10.6g"
In dieser Zeile stelle ich die Genauigkeit der Zahl ein. Maximal 10 Zeichen für die ganze Zahl und 6 Zeichen für den Bruchteil. Wenn wir einen zu großen Wert für diesen Bereich haben, werden alle Arten von
E-15 oder Ähnlichem angezeigt.
spaces_in_the_title = int((int(dials_precision[1:3])) / 2)
dials_precision ist eine Zeichenfolge, daher können wir einen Teil dieser Zeichenfolge, dh eine Art Teilzeichenfolge, nehmen. In diesem Fall müssen wir die Zahl 10 erhalten, also nehmen wir die Zeichen bei 1 und 2 Indizes, konvertieren diesen Teilstring in einen ganzzahligen Datentyp, teilen ihn durch zwei und runden ihn ab.
Wir benötigen diese Variable, damit die Beschriftungen in der Tabellenüberschrift auf der Zelle zentriert sind
length_of_table_lower_bound = (int(dials_precision[1:3]) + 2) * 4 + 5
Wie der Name schon sagt, ist diese Variable für die Länge der unteren Grenzen der Zellen der Wertetabelle der Funktion verantwortlich. Insgesamt nimmt die Zahl 10 Positionen ein, was bedeutet, dass die Spalte nicht kleiner als 10 sein darf. Wenn wir Zahlen mit dem oben beschriebenen e-15-Format erhalten, nimmt der Wert 11-12 Positionen ein. Deshalb fügen wir zu 10 eine weitere Zwei hinzu.
4 ist verantwortlich für die Anzahl der Spalten (x, y1, y2, y3) und 5 ist für die Anzahl der Zeichen, die die Zelle in einer Zeile begrenzen.
Der Rest der Variablen scheint intuitiv zu sein. Fahren wir also mit dem Drucken der Platte fort
print("|" + (spaces_in_the_title + 1) * delimiter + 'x' + spaces_in_the_title * delimiter + '|' + spaces_in_the_title * delimiter + "y1" +\ spaces_in_the_title* delimiter\ + '|' + spaces_in_the_title * delimiter + 'y2'\ + spaces_in_the_title * delimiter + '|' +\ spaces_in_the_title * delimiter\ + "y3" + spaces_in_the_title * delimiter + "|\n"\ + length_of_table_lower_bound * '-')
Wenn wir den gesamten Code verbinden, den wir bereits geschrieben haben, sehen wir in der Konsole Folgendes:
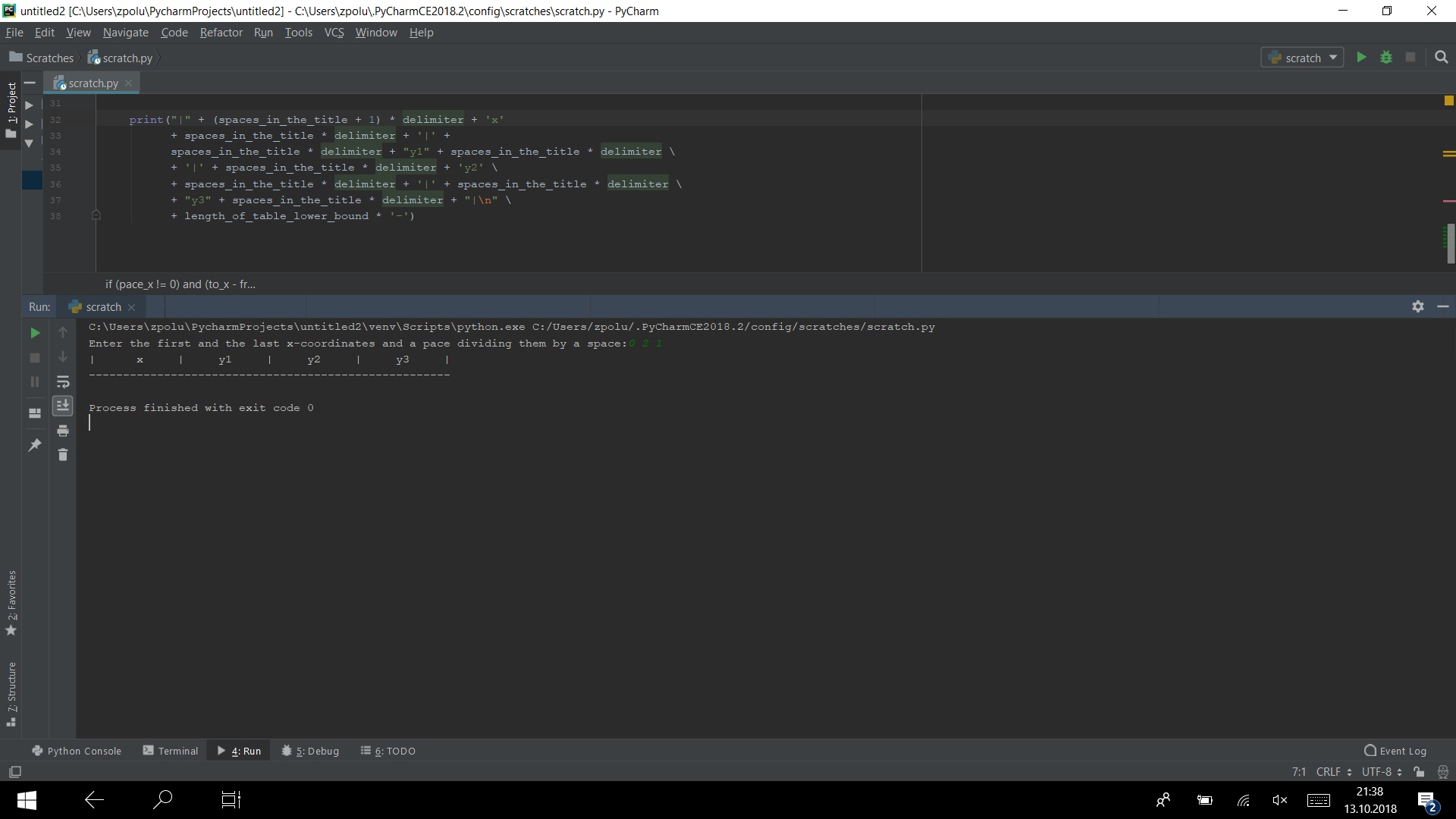
Jetzt müssen wir die Werte selbst drucken. Dazu benötigen Sie eine Schleife. Da die eingegebenen Daten möglicherweise gebrochen sind, funktioniert die Verwendung des
Bereichs nicht. Daher verwende ich eine reguläre Schleife.
Da wir sowohl eine abnehmende als auch eine zunehmende Folge von X haben können, müssen die Zyklusbedingungen so eingestellt werden, dass diese beiden Optionen berücksichtigt werden. Wir haben eine zuvor erstellte Variable, die die Antwort über die Art der Sequenz in Form von 0 oder 1 speichert. Daher reicht es aus, zwei Fälle zu berücksichtigen und für jeden die entsprechende Bedingung auszuwählen
while(is_sequence_decreasing and x_copy >= to_x) or\ (not is_sequence_decreasing and x_copy <= to_x):
Da wir für den Graphen das Minimum und Maximum des Graphen y1 benötigen, den wir zeichnen werden, führen wir spezielle Variablen ein, die für min und max verantwortlich sind
y1_cur_value = y1(x_copy) min_y1_value = (min_y1_value > y1_cur_value) * y1_cur_value + \ (min_y1_value <= y1_cur_value) * min_y1_value max_y1_value = (max_y1_value < y1_cur_value) * y1_cur_value + \ (max_y1_value >= y1_cur_value) * max_y1_value negative_value_exists += y1_cur_value < 0
Die Konstruktion wiederholt im Wesentlichen die Konstruktion von
if: ... else: ... nur durch boolesche Ungleichungen.
y1_cur_value speichert den aktuellen Wert der Funktion. Ich habe eine Variable erstellt, um eine Funktion nicht ständig aufzurufen, wenn ihr Wert an einem Punkt benötigt wird.
Wir werden auch das Vorhandensein negativer Werte für das Plotten benötigen.

Drucken Sie nun die Werte direkt aus. Ich möchte, dass alles in jeder Zelle schön und zentriert ist, daher muss ich jeden Wert manuell verarbeiten, um die Länge der Zahl zu überprüfen und die Anzahl der Leerzeichen abhängig davon auszuwählen, um den Wert auszurichten.
Hinweis
Das buchstäbliche Zentrieren der Nummer funktioniert nicht. Die für die Genauigkeit verantwortliche Variable hat den Parameter g. Er sagt, dass eine bestimmte Anzahl von Positionen für Nummern für eine Nummer reserviert ist (in unserem Fall standardmäßig 10). Wenn 10 Ziffern nicht gewählt werden, befinden sich leere Positionen links von den gefüllten Positionen. Daher können wir nur eine Reihe von 10 Positionen zentrieren.
aux_x = dials_precision % x_copy aux = len(aux_x) != int(dials_precision[1:3]) + 2 aux_2 = len(aux_x) == int(dials_precision[1:3]) + 1 print('|' + delimiter * aux + aux_x + delimiter * (aux - aux_2) + '|', end='')
aux_x - eine Zeichenfolge, die bereits mit einer bestimmten Genauigkeit in eine Ansicht gebracht wurde. Jetzt müssen wir die Länge der Nummer überprüfen und die erforderliche Anzahl von Leerzeichen auswählen. Da auf jeder Seite nicht mehr als ein Leerzeichen benötigt wird, eignen sich
bool eva-Variablen perfekt als Hüter der Anzahl dieser Leerzeichen.
aux_2 fängt den Fall ab, wenn die Länge der Zahl 11 beträgt.
Wir tun dies auch für die Werte von drei Funktionen
aux_y1 = dials_precision % y1_cur_value aux = len(aux_y1) != int(dials_precision[1:3]) + 2 aux_2 = len(aux_y1) == int(dials_precision[1:3]) + 1 print(delimiter * aux + aux_y1 + delimiter * (aux - aux_2) + '|', end='') if (x_copy != 0): aux_y2 = dials_precision % y2(x_copy) aux = len(aux_y2) != int(dials_precision[1:3]) + 2 aux_2 = len(aux_y2) == int(dials_precision[1:3]) + 1 print(delimiter * aux + aux_y2 + delimiter * (aux - aux_2) + '|', end='') aux_y3 = dials_precision % y3(x_copy) aux = len(aux_y3) != int(dials_precision[1:3]) + 2 aux_2 = len(aux_y3) == int(dials_precision[1:3]) + 1 print(delimiter * aux + aux_y3 + delimiter * (aux - aux_2) + \ "|\n" + length_of_table_lower_bound * '-') else: print((spaces_in_the_title - 2) * delimiter + " " \ + (spaces_in_the_title - 2) * delimiter + '|' \ + (spaces_in_the_title - 2) * delimiter + " " \ + (spaces_in_the_title - 2) * delimiter + "|\n" \ + length_of_table_lower_bound * '-') x_copy += pace_x
Wie ich ganz am Anfang sagte, haben die zweite und dritte Funktion Haltepunkte - beide Funktionen existieren am Punkt x = 0 nicht. Daher müssen wir auch diese Fälle erfassen.
Vergessen Sie nicht, den aktuellen x-Wert zu erhöhen, damit wir keinen endlosen Zyklus erhalten.
Sammeln wir den gesamten Code in einem Programm und führen Sie ihn beispielsweise auf dem Test -1,2 3,6 0,3 aus
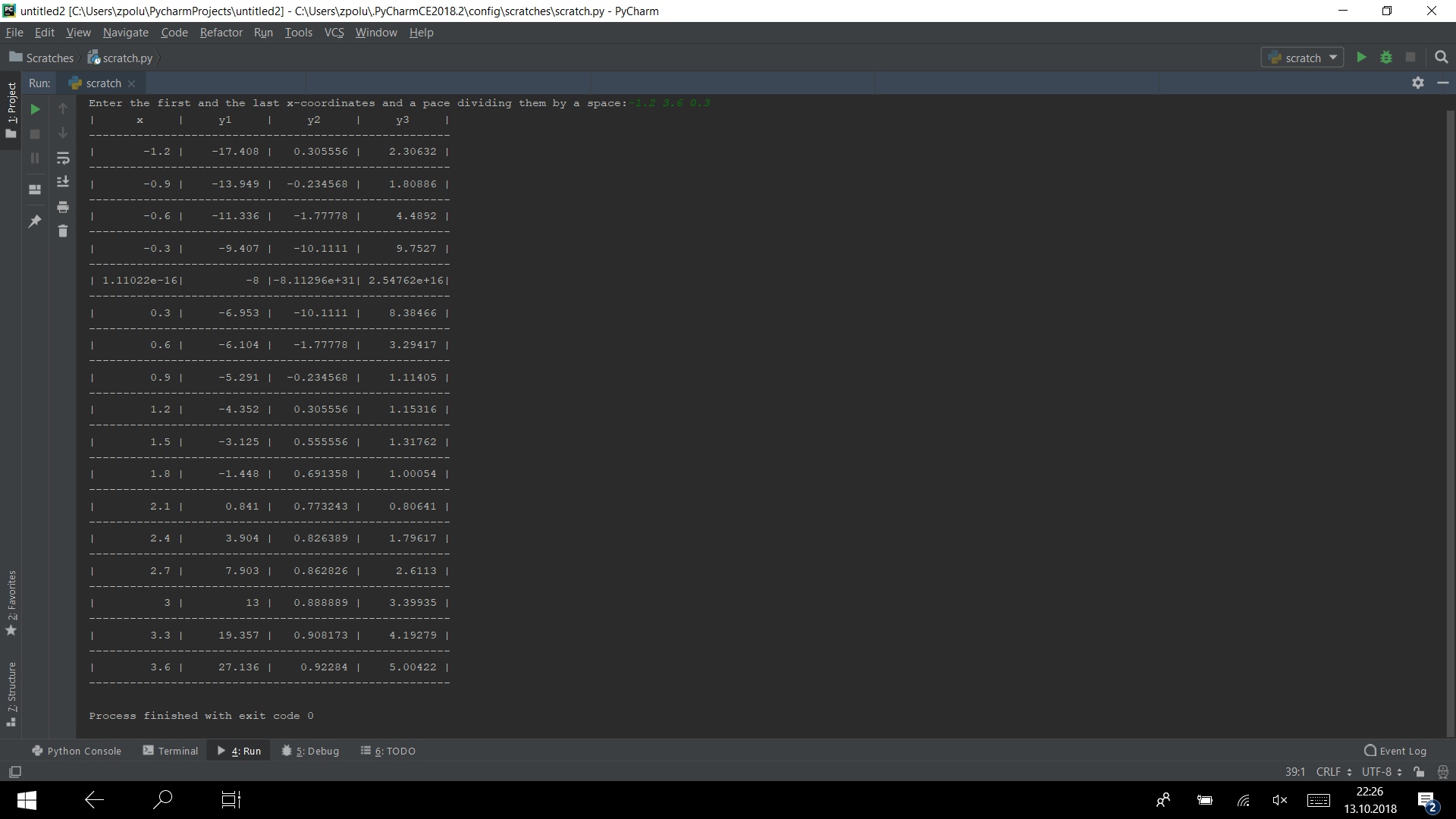
from math import sqrt def y1(x): return x**3 - 2*x**2 + 4*x - 8 def y2(x): return 1 - 1/x**2 def y3(x): return sqrt(abs(y1(x)*y2(x))) from_x, to_x, pace_x = map(float, input("Enter the first and the last"\ " x-coordinates and a pace dividing them by a"\ " space:").split()) if (pace_x != 0) and (to_x - from_x)*pace_x >= 0 and abs(to_x - from_x): dials_precision = "%10.6g"
Im zweiten Teil dieser Erstellung werden wir Diagramme erstellen
 Fortsetzung folgt ...
Fortsetzung folgt ...