Spiel mit Mathe-Diagrammen anstelle von Diagrammen

In diesem Screenshot sehen Sie ein scheinbar gewöhnliches Spiel mit Pixelgrafiken. Es ist jedoch nicht alles so einfach.

Das Relief der Erde ähnelt stellenweise einer Sinuskurve, und die Kugeln ähneln zwei symmetrischen Graphen der Wurzel von x.

Tatsächlich bezieht sich alles, was Sie auf die eine oder andere Weise auf dem Bildschirm sehen, auf Mathematik, mathematische Kurven und Grafiken.

Hintergrund

Einmal stieß ich beim Ansehen des Videos des Senders „Numberphile“ auf ein sehr interessantes Videomaterial namens „The Formula of Everything“ .

In diesem Video wurde Tappers selbstreferenzielle Formel vorgestellt, die mit einem bestimmten Wert von k das Bild in der Grafik neu erstellte. Diese Formel sieht folgendermaßen aus:

$$

$$\ frac {1} {2} <\ lfloor mod (\ lfloor \ frac {y} {17} \ rfloor 2 ^ {-17 \ lfloor x \ rfloor - mod (\ lfloor y \ rfloor, 17)}, 2 ) \ rfloor$$

Diese Formel hat mich wirklich interessiert und ich hatte eine Idee:

"Und was ist, wenn Sie ein Spiel erstellen, bei dem anstelle gewöhnlicher Texturen, die in verschiedenen Dateien im PNG- und JPG-Format gespeichert sind, mathematische Grafiken und Kurven verwendet werden?"

Diese Idee erschien mir ziemlich interessant und schwer umzusetzen.

Die Aufgaben

Ich stand vor folgenden Aufgaben:

• Überlegen Sie sich die Bedeutung des Spiels, das Gameplay
• Leiten Sie Formeln ab, deren Diagramme die Silhouetten von Zeichen, Aufzählungszeichen und Oberflächen sind, die ich benötige
• Implementiere das alles im Spiel

Gameplay und Bedeutung des Spiels

Das Gameplay und die Bedeutung des Spiels haben sich während der Entwicklung dieses Spiels mehrmals geändert. Dies alles ist darauf zurückzuführen, dass es insbesondere bei der Ableitung von Formeln für bestimmte Silhouetten einige Schwierigkeiten gab. Aber im Allgemeinen handelt dieses Spiel von einer einsamen fliegenden Untertasse, die um die Planeten fliegt, sie erforscht und Feinde tötet, die ihr im Weg stehen.

Formeln und ihre anschließende Implementierung im Spiel

Ich habe die folgenden zwei Absätze zu einer Unterüberschrift zusammengefasst, da es nicht praktikabel ist, zwischen einer Formel und ihrer Implementierung zu „überspringen“.

Um das Spiel zu erstellen, wurden die Programmiersprache c ++ und die SFML-Bibliothek ausgewählt, um Fenster zu erstellen und etwas darauf zu zeichnen.

Da ich in der Schule bin und erst kürzlich herausgefunden habe, was eine Sinuskurve ist und wie sie aussieht, hatte ich ziemlich große Probleme, verschiedene Formeln abzuleiten. Meistens endete dies mit einer einfachen Auswahl.

Am Ende des Artikels befindet sich ein Link zu GitHub, auf dem der gesamte Code veröffentlicht wird. In dem Artikel werden nur kleine Codeteile angegeben, um sie nicht zu verunreinigen.

Planetenoberfläche

Für die Oberfläche des Planeten habe ich die folgende Formel abgeleitet:

$$

$$f (x) = | sin (x) |$$

Eine ziemlich einfache Formel, aber bei der Implementierung bestand die Notwendigkeit, die Höhe und Länge einer bestimmten Sinuskurve zu steuern. Um die Krümmung des Reliefs zu vermeiden, wird x mit π multipliziert. Daher sieht der endgültige Code folgendermaßen aus:

int groundC = ceil(abs(sin(((i+1)*groundScale*M_PI)))*groundHeight); 

Textur des Planeten im Weltraum

Die Textur des Planeten besteht aus einem Kreis und einem Muster darauf. Das Spiel hat 4 Formeln zum Erstellen von Mustern und 12 Texturen von Planeten mit einem anderen Muster. Abhängig vom "Schritt" der Formel werden verschiedene Muster erstellt. Wenn ein Planet erzeugt wird, wird er pseudozufällig auf Farbe, Größe und Position im Raum eingestellt.

Kugeln

Bild einer Kugel aus dem Spiel. Die Kugel ist gedreht.

Für Kugeln wurde eine sehr einfache Formel gewählt:

$$

$$\ sqrt {x}$$

Die Darstellung dieser Formel spiegelt sich auf der Abszisse wider.

Protagonist

Also kamen wir zu den komplexesten Formeln.

Ich habe die Formel des Protagonisten mit großer Schwierigkeit abgeleitet. Es sieht so aus:

$$

$$\ sqrt {x ^ {\ frac {1} {2.8}} + x ^ {10.9-x ^ {9.3-x}}} - 0.3$$

Ja, eine sehr krumme, sehr hässliche Formel. Aber die Hauptsache ist nicht die Formel, das Hauptergebnis.

Um das Ergebnis zu erzielen, wollte ich mich zunächst nur mit einem bestimmten Schritt entlang der x-Achse bewegen, die y-Koordinaten aufschreiben und dann alle diese Punkte verbinden, um so unsere Platte zu erhalten. Aber dann habe ich versehentlich einen zu kleinen Schritt gemacht, und mein ganzer Teller ragte wunderschön heraus, mit Ausnahme von zwei Endpunkten, die sich schließlich verbanden. Infolgedessen sieht die Platte folgendermaßen aus:



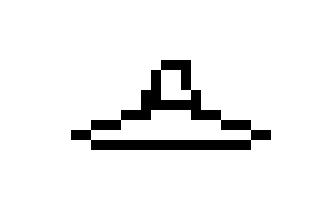
Als nächstes brauchten wir die Textur des Protagonisten im Raum. Es sieht so aus:



Es basierte auf einem Kreis. Die Hauptkabine wird nach folgender Formel hergestellt:

$$

$$(x ^ {7-x}) ^ {\ frac {0.8} {x}}$$

Der Graph dieser Formel wird entlang der Ordinatenachse gespiegelt.

So sieht diese Formel in c ++ aus:

 int x = round(pow(pow(i, 7 - i), 0.8 / i)); 

Feinde und ihr Spawner

Rechts im Bild ist ein blauer Laicher, rote Objekte sind Feinde.

Spauner ist ein gewöhnlicher Planet mit einem ungewöhnlichen Muster. Dieses Muster ist ein Diagramm der Formel:

$$

$$sin (x) * x ^ {0,8}$$

Enemy Texture Formula:

$$

$$(x ^ {3-x}) ^ {\ frac {1} {x}}$$

Bäume

Ich gebe zu, ich konnte keine Formel zum Erstellen der Silhouette von Bäumen ableiten oder auswählen. Um jedoch nicht gegen das Grundkonzept des gesamten Spiels und die Regeln zu verstoßen, keine Dateien im PNG- und JPG-Format zu verwenden, habe ich einen Trick verwendet. Ich habe Fraktale verwendet , um Bäume zu erstellen.


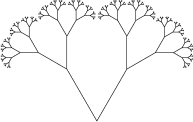Beispiel für einen Fraktalbaum

Höchstwahrscheinlich werden Sie zustimmen, dass fraktale Bäume selbst ziemlich langweilig aussehen. Wenn Sie beispielsweise einige zufällige Elemente hinzufügen, wachsen möglicherweise nicht unbedingt 2 Zweige, sondern auch 3 oder 1 oder gar nicht. Es ist auch nicht möglich, überall den gleichen Neigungswinkel herzustellen.

Natürlich könnte man einen gewöhnlichen Maschinenpseudorand erstellen , der auf Computer-Ticks basiert, aber die folgende Idee schien mir interessanter:

"Und was ist, wenn jeder Baum eine bestimmte Zahl (Startwert) erhält, aus der Pseudozufallszahlen berechnet werden, die die Parameter des Baums beeinflussen?"

Glücklicherweise verfügt c ++ über eine separate Pseudorandum-Bibliothek.

Infolgedessen sehen die generierten Bäume folgendermaßen aus:



Links ist ein Baum mit Samen 13 und rechts - 22

Und der Code, der diese Bäume generiert, lautet:

 Branch Branch::createNewBranch(Branch cur, Tree* parent, float angleMultiplier, int level) { Vector2f sp(cur.startPoint.x, cur.startPoint.y); float randomAngle = ((*parent).getRand() * 15) - 5; float t = cur.thickness * 0.75; float l = cur.length * 0.67; float a = cur.angle + 30*angleMultiplier + randomAngle; sp.y -= (cos((cur.angle-180)*3.1415926 / 180) * cur.length); sp.x += (sin((cur.angle-180)*3.1415926 / 180) * cur.length); Branch gen(sp, t, l, a, level); if (level > 0) { int count = 100 * (*parent).getRand(); if (count >= 25 && count < 80) { //     ,      && count < 80,        ,  . , -          20%  10%,  ,    count<90 (*parent).addBranch(gen.createNewBranch(gen, parent, 1, level - 1)); (*parent).addBranch(gen.createNewBranch(gen, parent, -1, level - 1)); } if (count >= 80) { //    ,    count >= 90 if (count % 2 == 0) { (*parent).addBranch(gen.createNewBranch(gen, parent, -1, level - 1)); } else { (*parent).addBranch(gen.createNewBranch(gen, parent, 1, level - 1)); } } } return gen; } 

Hinweis Ja, ich weiß, dass ich einige Variablen „fest codiert“ habe, aber bitte beschuldigen Sie mich nicht dafür. Ich dachte, dass es keinen Sinn macht, separate konstante Variablen zu erstellen, die im Prinzip nur die Chance beeinflussen, einen neuen Zweig zu erstellen.

Noch etwas Code

Oben habe ich Code nur zum Generieren von Texturen bereitgestellt. In diesem Untertitel werde ich den Code des Spiels selbst beschreiben. Der gesamte Code befindet sich auf GitHub, der Link zum Projekt ist abgeschlossen .

Spieler

Der Player verfügt über zwei verschiedene Aktualisierungsmethoden - spaceUpdate und planetUpdate. Dementsprechend aktualisiert spaceUpdate den Player, wenn er sich im Weltraum befindet, planetUpdate - wenn er sich auf dem Planeten befindet. Auf dem Planeten werden die Beschleunigung und Geschwindigkeit des Spielers berechnet. Abhängig von der Horizontalbeschleunigung ändert sich der Neigungswinkel der Platte von 30 Grad auf -30 Grad. Wenn Sie sich den Barrieren nähern, nimmt die Geschwindigkeit des Spielers ab. Solche Barrieren existieren für die x-Achse (0; mapSize.x) und für die y-Achse. Für die y-Achse sind die Dinge etwas komplizierter. Es gibt eine Mindesthöhe, die wie folgt berechnet wird: Die Mindesthöhe der Erde wird zur Höhe der Sinuswelle addiert und die Höhe der Bäume wird addiert. Die Höhe der Bäume wird auf sehr einfache Weise berechnet - die anfängliche Länge des Zweigs multipliziert mit der Anzahl der Zyklen, die während der Erzeugung des Baums ausgeführt wurden. Es gibt keinen oberen Rand - der Spieler fliegt von oben aus der Karte heraus, wechselt zu spaceUpdate und das Leerzeichen wird gezeichnet.

SpaceUpdate funktioniert wie folgt: Die Beschleunigung und Geschwindigkeit des Spielers werden berechnet. Als nächstes wird der Drehwinkel des Spielers berechnet. Der Winkel wird wie folgt berechnet: Wenn die Beschleunigung Null ist, wird der Winkel relativ zur Geschwindigkeit des Spielers berechnet, wenn nicht, relativ zur Beschleunigung. Auch im Weltraum hat der Spieler die Möglichkeit zu schießen. Das Schießen erfolgt wie folgt: Eine Kugel wird mit einer Drehung wie bei einem Spieler erstellt und der Liste hinzugefügt. Wenn Sie einen Spieler im Weltraum aktualisieren, wird auch jede Kugel in dieser Liste aktualisiert. Beim Rendern eines Spielers werden auch Kugeln gezogen. Auch im Weltraum sind die Dinge mit Barrieren etwas komplizierter. Der Weltraum ist in Sektoren unterteilt, in jedem Sektor 4 Planeten, insgesamt 1 000 000 Planeten und 25 000 Sektoren. Jeder Sektor hat eine eindeutige ID. Wenn der Rest beim Teilen durch 500 gleich 0 ist - es gibt eine linke Barriere, wenn der Rest von 499 rechts ist, wenn beim Teilen durch 500 das Ergebnis 0 ist - ist die obere Barriere vorhanden, wenn 499 die obere ist. Wenn es keine Barrieren gibt, bewegt sich der Spieler beim Verlassen des Rahmens in den entsprechenden Sektor.

Raum

Ich habe das meiste bereits skizziert, aber es bleiben noch einige Dinge übrig. In jedem Raumsektor gibt es 4 Planeten. Wenn ein Spieler die E-Taste drückt und sich in einem Radius von diesem Planeten befindet, bewegt er sich zum Planeten.

Feinde

Die KI der Feinde ist sehr dumm - wenn sich ein Spieler im Radius ihrer Sicht befindet, neigen sie einfach dazu, darauf zu stoßen, und es gibt einen kleinen Fehler, so dass ihr Weg eine ziemliche Kurve ist. Befindet sich kein Spieler im Radius ihrer Sichtbarkeit, werden sie zu ihrem Spawner geschickt.

Spawner

In jedem Raumbereich gibt es 1 Laicher. Spauner können unterschiedlich groß sein. Die Größe beeinflusst die Sichtbarkeit des Players. Befindet sich der Spieler in seiner Sichtzone, erstellt der Spawner alle 5 Sekunden Feinde, die Anzahl der Feinde darf jedoch 10 nicht überschreiten.

Fazit

Nachdem ich ungefähr eine Woche verbracht hatte, erstellte ich ein Spiel, das keine .png- oder .jpg-Dateien verwendet.

Link zum Projekt auf GitHub

Für diejenigen, die zu faul sind, um das Projekt herunterzuladen und das Spiel auszuführen, ein kurzes Video zum Gameplay: